Вывод и применение уравнения Нернста
Добавил пользователь Skiper Обновлено: 21.01.2026
Электрод – система, состоящая из проводника 1-го рода (металл, уголь), находящегося в контакте с проводником 2-го рода (раствор, расплав), носителем которого являются ионы.
Электрод представляет собой электрохимическую систему, которая состоит как минимум из двух фаз. На границе раздела фаз протекают гетерогенные реакции, в результате которых происходит переход заряженных частиц через границу раздела, что сопровождается образованием на этой границе ДЭС (двойного электрического слоя).
Равновесные процессы передачи электронов, записываемые как Ox + zē D Red, называются потенциалопределяющими.
Потенциал является электрической характеристикой электрода.
Потенциал электрохимической системы, измеренный при стандартных условиях, называется стандартным электродным потенциалом, единица измерения – В.
Для системы Ox + zē D Red обозначается как φ 0 Ox/Red.
Абсолютные значения стандартных потенциалов не определяются. Значения электродных потенциалов обычно берутся относительно системы H + + ē → ½H2 0 , у которой стандартный потенциал принят за 0. Стандартные потенциалы окислительно-восстановительных систем приводятся в таблицах.
Величины стандартных потенциалов металлов (φ 0 ) являются мерой восстановительной способности их атомов и мерой окислительной способности ионов металлов. Чем более отрицательное значение имеет потенциал системы Ме z + /Ме, тем более сильной восстановительной способностью обладает атом. И наоборот, чем более положителен потенциал металлического электрода, тем более сильной окислительной способностью обладают его ионы. Например, к наиболее сильным восстановителям (в водном растворе) относится литий (φ 0 Li + /Li = -3,04 B), а к наиболее сильным окислителям – ионы золота Au 3+ , Au + (φ 0 Au 3+ /Au = +1,50 B, φ 0 Au + /Au = +1,69 B).
Потенциал электрохимической системы зависит от природы металла и электролита, температуры, концентрации электролита.
Для процесса Ox + zē D Red эта зависимость выражается уравнением Нернста:
где φ 0 Ox/Red– стандартный электродный потенциал;
z – число электронов, участвующих в данной потенциалопределяющей реакции;
R – универсальная газовая постоянная (8,31 );
T – температура, К;
F – постоянная Фарадея (96500 );
aox, ared – активности окисленной и восстановленной форм.
Для разбавленных растворов, где активность приблизительно равна концентрации, при 298 К, после подстановки постоянных величин уравнение примет вид:
При записи электродов, вертикальной чертой (│) обозначают границу раздела фаз металл – электролит и придерживаются следующих правил:
1) слева указываются вещества, находящиеся в растворе; справа – вещества, образующие другую фазу или электродный материал:
2) если одна фаза содержит несколько веществ, то их символы разделяют запятыми:
3) при записи уравнения электродной реакции слева указывают вещества в окисленной форме и электроны, справа вещества в восстановленной форме: Ox + zē D Red
Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
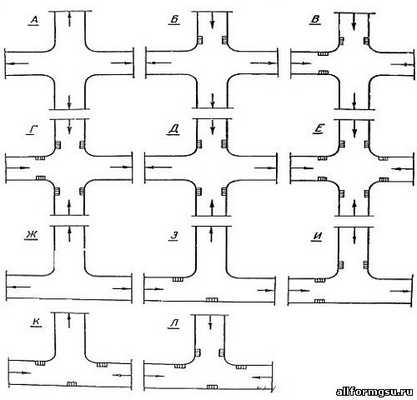
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
© cyberpedia.su 2017-2020 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!
Вывод и применение уравнения Нернста
Равновесие между химическими и электрическими движущими силами определяет величину мембранного потенциала покоя. Состояние равновесия достигается, когда различие в свободной энергии этих сил равно нулю (другими словами, когда общий поток = 0):
Изменение свободной энергии, происходящее при движении через мембрану компонента X, можно выразить уравнением:
• R — газовая постоянная (2 кал моль-1 К-1)
• Т — абсолютная температура (К; 37 °С = 307,5 К)
• [Х]0 — концентрация X вне клетки
• [X]i — концентрация X внутри клетки
и изменение свободной энергии, обусловленное транспортом через мембрану заряда, связанного с растворенным компонентом X составляет:
• Em — равновесный потенциал (в вольтах)
• z — валентность иона (электрический заряд)
• F— число Фарадея (2,3 х 104 кал вольт-1 моль-1)
В состоянии равновесия
и после преобразования получаем.
Таким образом, значение равновесного потенциала или потенциала Нернста для одновалентного иона X при 37 °С определяется уравнением:
Если концентрация ионов известна, то уравнение Нернста можно использовать для расчета равновесного мембранного потенциала для каждого иона в отдельности. На рисунке ниже показаны результаты таких расчетов для плазматической мембраны мышечных клеток. Так, для [К+]0 = 4 мМ и [K+]i = 155 мМ значение мембранного потенциала Еm = -98 мВ, если учитывать только поток ионов К+, т. е. Еm = Еk.
Почти во всех покоящихся клетках млекопитающих плазматическая мембрана проницаема для ионов К+. Na+/К+-АТФаза поддерживает трансмембранный ионный градиент и создает внутри клетки относительно высокую концентрацию ионов К+ ([K+]i). При открытии некоторых К+-каналов ионы К+ начинают транспортироваться в направлении градиента концентрации, что приводит к появлению положительного заряда с внешней стороны мембраны и отрицательного с внутренней ее стороны. Этот отрицательный мембранный потенциал, Еm, представляет собой электродвижущую силу, которая препятствует дальнейшему выходу К+ из клетки в направлении градиента (химическая движущая сила). Таким образом, открытие в покоящейся клетке специальных селективных К+-каналов определяет значение отрицательного потенциала покоя, при котором не происходит транспорта К+ через мембрану и величина Еm остается постоянной.
Аналогично потенциал Нернста можно рассчитать и для других ионов. Если мембрана становится более проницаемой для определенных ионов, то мембранный потенциал Еm будет меняться, приближаясь к значению потенциала Нернста для этих ионов (обычно становясь более положительным при деполяризации мембраны).
Например, если плазматическая мембрана становится более проницаемой для ионов Na+, то они будут транспортироваться в направлении своего градиента концентрации. При этом мембрана будет приобретать отрицательный заряд с внешней стороны и положительный заряд с внутренней. В физиологических условиях, в покоящейся клетке, открытие нескольких Na+-каналов, наряду с постоянным притоком зарядов за счет протечки, приведет к поступлению Na+ в клетку, и значение мембранного потенциала покоя сдвинется в более положительную сторону (например, -82 мВ). Напротив, аналогичный расчет в случае ионов К+ показывает, что значение мембранного потенциала покоя составит -89 мВ. В клетках, обладающих меньшей проницаемостью для ионов К+ в результате фоновой утечки ионов Na+ и деполяризующих ионных потоков, величина мембранного потенциала покоя Em смещается в сторону более положительных значений (например, становится равной -50 мВ). При возбуждении клетки электрическим зарядом и открытии Na+ каналов, в состоянии теоретического равновесия между потоком Na+, направленным в клетку, и потоком К+, направленным в противоположную сторону, уровень мембранного потенциала оказывается ближе к ENa, а не к Ек. Согласно уравнению Нернста, равновесный потенциал для Na+ при 37 °С составляет:
Если [Na+]0 = 145 мМ и [Na+]i = 12 мМ (как для клеток мышц), то значение мембранного потенциала составляет Еm = +67 мВ, принимая во внимание транспорт только ионов Na+. Таким образом, суммарный эффект открытия Na+ каналов выражается в установлении потока ионов натрия, направленного в клетку, что приводит к сдвигу отрицательного потенциала покоя Еm до значения +67 мВ.
Аналогичным образом, когда плазматическая мембрана становится более проницаемой для Са2+, ионы транспортируются в направлении градиента концентрации. При этом мембрана на внешней стороне приобретает более отрицательный заряд, а на внутренней — более положительный. Когда под действием электрического заряда клетка возбуждается и открываются Са2+-каналы, теоретическое равновесие между потоком Са2+ в клетку и потоком К+ из клетки определяет уровень мембранного потенциала ближе к значению ЕCa. Согласно уравнению Нернста,
Если [Са2+]0 = 1,5 мМ и [Ca2+]i = 0,1 мкМ, как для мышечной клетки, то мембранный потенциал составляет Em = +129 мВ. Таким образом, суммарный эффект открытия Са2+ каналов выражается в установлении потока Са2+ в клетку, который приводит к сдвигу отрицательного потенциала покоя Еm, к +129 мВ. [Са2+-каналы открываются при более положительном значении потенциала действия, чем натриевые каналы. Это означает, что они открываются на более поздней фазе потенциала действия. Для ионов Cl_ по уравнению Нернста получаем
Если [Cl-]0 = 123 мМ и [Cl-]i= 4,2 мМ, то мембранный потенциал только для Cl- составляет Еm = -90 мВ. Таким образом, суммарный эффект открытия хлоридного канала приводит к выходу ионов Cl-, что стабилизирует отрицательное значение потенциала покоя Еm.
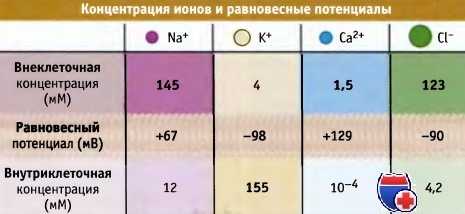
Концентрация свободных ионов и равновесные потенциалы клеток скелетных мышц млекопитающих.
Значения равновесных потенциалов рассчитаны для 37 °С, принимая величину потенциала покоя мембраны мышечной клетки равной -90 мВ.
Сверху обозначены относительные радиусы негидратированных ионов.
Редактор: Искандер Милевски. Дата обновления публикации: 18.3.2021
Уравнение Нернста и его различные формы
соответствует наиболее общая форма уравнения Нернста:
Если заменить натуральный логарифм десятичным и подставить соответствующие значения постоянных величин в предлогарифмическом сомножителе, то для температуры 298 К уравнение имеет вид
В дальнейшем будем пользоваться округленным значением числовой константы в логарифмическом слагаемом, что значительно упрощает расчеты, не внося в их результат существенной ошибки:
Например, для полуреакции
Sn 4+ + 2e – D Sn 2+
уравнение Нернста имеет вид:
В различных частных случаях, в зависимости от характера полуреакции, уравнение Нернста записывается по-разному:
aA + bB + . + ne – D mM + nN + .
Например, для окислительно-восстановительной системы
потенциал выражается уравнением
Обратим внимание на то, что в достаточно разбавленных водных растворах концентрацию воды можно считать величиной постоянной, поэтому она не фигурирует в знаменателе дроби, но в неявном виде входит в состав константы Е 0 . Данная форма уравнения Нернста соответствует тому весьма распространенному и важному случаю, когда окислительно-восстановительное равновесие протекает с участием среды.
2. Если окислительно-восстановительная система включает в себя малорастворимое вещество, то его концентрация, будучи также величиной постоянной, не включается в логарифмический член уравнения Нернста. Так, для полуреакции
уравнение Нернста имеет вид
3. Для металлических электродов, то есть для окислительно-восстановительных систем, представляющих собой металл, контактирующий с раствором, содержащим катионы этого же металла, например, для электрода
уравнение Нернста включает только концентрацию катионов металла в растворе, то есть
4. Если окислительно-восстановительная система включает в себя малорастворимый в воде газ (H2, O2, N2 и т.д.), то в уравнение Нернста входит не концентрация этого газа, а его парциальное давление. Например, для системы
уравнение Нернста должно быть записано следующим образом:
Однако в обычных условиях парциальное давление газа равно атмосферному, раствор насыщен этим газом, следовательно, еcть величина постоянная, и она входит в константу Е 0 , поэтому для данного случая
29. Электрохимический ряд активности металлов (ряд напряжений, ряд стандартных электродных потенциалов) — последовательность, в которой металлы расположены в порядке увеличения их стандартных электрохимических потенциалов φ 0 , отвечающих полуреакции восстановления катиона металла Me n+ : Me n+ + nē → Me
Ряд напряжений характеризует сравнительную активность металлов в окислительно-восстановительных реакциях в водных растворах.
| Li→Rb→K→Ba→Sr→Ca→Na→Mg→Al→Mn→Cr→Zn→Fe→Cd→Co→Ni→Sn→Pb→H→Sb→Bi→Cu→Hg→Ag→Pd→Pt→Au |
30.Схема гальванического элемента
На аноде протекает процесс окисления цинка:
В результате этого атомы цинка превращаются в ионы, которые переходят в раствор, а цинковый анод растворяется, и его масса уменьшается. Обратите внимание, что анод в гальваническом элементе является отрицательным электродом (за счет электронов, полученных от атомов цинка) в отличие от процесса электролиза, где он подключается к положительном полюсу внешней батареи.
Электроны от атомов цинка по внешней электрической цепи (металлическому проводнику) движутся к катоду, где протекает процесс восстановления ионов меди из раствора ее соли:
В результате этого образуются атомы меди, которые осаждаются на поверхности катода, и его масса увеличивается. Катодом в гальваническом элементе является положительно заряженный электрод.
Суммарное уравнение реакции, протекающей в медно-цинковом гальваническом элементе, можно представить так:
Zn + Cu 2+ = Zn 2+ + Cu.
Фактически протекает реакция замещения меди цинком в ее соли. Эту же реакцию можно осуществить и иным способом — погрузить цинковую пластинку в раствор CuSO4. При этом образуются те же самые продукты — медь и ионы цинка. Но отличие реакции в медно-цинковом гальваническом элементе в том, что процессы отдачи и присоединения электронов пространственно разделены. Процессы отдачи (окисление) и присоединения (восстановление) электронов происходят не при непосредственном контакте атома Zn с ионом Сu 2+ , а в разных местах системы — соответственно на аноде и на катоде, которые соединены металлическим проводником. При таком способе проведения этой реакции электроны перемещаются от анода к катоду по внешней цепи, представляющей собой металлический проводник. Направленный и упорядоченный поток заряженных частиц (в данном случае электронов) и естьэлектрический ток. Во внешней цепи гальванического элемента возникает электрический ток.
31. Гальванический элемент. ЭДС гальванического элемента
Рассмотрим простейший гальванический элемент Даниэля – Якоби, состоящий из двух полуэлементов – цинковой и медной пластин, помещенных в растворы сульфатов цинка и меди соответственно, которые соединены между собой посредством электролитического ключа – например, полоски бумаги, смоченной раствором какого-либо электролита. Схематически данный элемент изображается следующим образом:
Zn / Zn 2+ // Cu 2+ / Cu
На поверхности каждого из электродов имеет место динамическое равновесие перехода ионов металла из электрода в раствор и обратно, характеризуемое потенциалом ДЭС (зарядом на электроде q). Если соединить медный и цинковый электроды металлическим проводником, немедленно произойдет перераспределение зарядов – электроны начнут перемещаться с электрода с более отрицательным зарядом (в нашем случае – цинкового) на электрод с более положительным зарядом (медный), т.е. в проводнике возникнет электрический ток. Изменение величины заряда каждого из электродов нарушает равновесие – на цинковом электроде начнется процесс перехода ионов из электрода в раствор (окисление металла), на медном – из раствора в электрод (восстановление металла); при этом протекание процесса на одном электроде обусловливает одновременное протекание противоположного процесса на другом:
Электрод, на котором при работе гальванического элемента протекает процесс окисления, называется анодом, электрод, на котором идет процесс восстановления – катодом. При схематическом изображении гальванических элементов слева записывают анод, справа – катод (стандартный водородный электрод всегда записывают слева). Суммарный окислительно-восстановительный процесс, происходящий в гальваническом элементе, выражается следующим уравнением:
Сu 2+ + Zn o ––> Сu o + Zn 2+
Т.о., гальванический элемент можно определить как прибор для преобразования химической энергии окислительно-восстановительной реакции в электрическую за счет пространственного разделения процессов окисления и восстановления. Работа, которую может совершить электрический ток, вырабатываемый гальваническим элементом, определяется разностью электрических потенциалов между электродами (называемой обычно просто разностью потенциалов) ΔΦ и количеством прошедшего по цепи электричества q:
Работа тока гальванического элемента (и, следовательно, разность потенциалов), будет максимальна при его обратимой работе, когда процессы на электродах протекают бесконечно медленно и сила тока в цепи бесконечно мала. Максимальная разность потенциалов, возникающая при обратимой работе гальванического элемента, есть электродвижущая сила (ЭДС) гальванического элемента.
32. Электролиз. Последовательность разрядов ионов на электродах. Явление перенапряжения. Электролиз с растворимыми и нерастворимыми электродами.
Электролизом называется ОВ процесс, протекающий при пропускании постоянного электрического тока через раствор или расплав электролита. Возможные процессы: на катоде могут восстанавливаться ионы водорода, если среда кислая, ионы водорода из воды, если щелочная, ионы металла, на аноде могут окисляться кислотные остатки, могут окисляться гидроксид ионы, если среда щелочная, воды - если кислая или нейтральная.
Из растворов солей химически активные Ме, стоящие в ряду стандартных потенциалов до аллюминия включительно, на электроде не восстанавливаются, а восстанавливаются ионы водорода. На катоде легче всего восстанавливаются ионы менее активныхМе, стоящих в РСП после водорода. Из растворов солей Ме, которые расположены между аллюминием и водородом, восстанавливаются, но и возможно восстановление ионов водорода.
Процессы, протекающие при электролизе обратны процессам, идущим при работе гальвонического элемента: при электролизе химическоя реакция осуществляется за счёт энергии электрического тока, подводимой извне, в то время как при работе гальванического элемента энергия самопроизвольно протекающей в нём химической реакции превращается в электрическую энергию. Таким образом при электролизе возникает ГЭ (зарядка).
При рассмотрении анодных процессов следует иметь в виду, что на аноде может идти процесс окисления материала самого электрода. В связи с этим различают электролиз с растворимым и нерастворимым анодом. Нерастворимым называется анод, материал которого не претерпевает окисления в ходе электролиза. Растворимым называется анод, материал которого может окисляться в ходе электролиза. В качестве материалов для первого случая чаще всего применяют графит, уголь, платину. На нерастворимом аноде при электролизе водных растворов щелочей и фторидов происходит электрохимическое окисление воды с выделением кислорода. При электролизе водных растворов бескислородных кислот и их солей (кроме HF и фторидов) у анода разряжаются анионы (отрицательно заряженные ионы). Эта аномалия связана со значительным перенапряжением второго из этих процессов - материал анода оказывает тормозящее действие на процесс выделения кислорода.В случае растворимого анода число конкурирующих окислительных процессов возрастает до трёх : электрохимическое окисление воды с выделением кислорода, разряд аниона и электрохимическое окисление металла анода. Из этих возможных процессов будет идти тот, который энергетически наиболее выгоден. Если металл анода расположен в РСП раньше обеих других электрохимических систем, то будет наблюдаться анодное растворение металла. В противном случае будет идти выделение кислорода или разряд аниона.
Перенапряжение - это дополнительное напряжение, необходимое для того, чтобы прцесс электролиза пошёл. Чтобы процесс электролиза протекал, внешнее напряжение должно быть по крайней мере равно ЭДС возникшего ГЭ. Это напряжение называется теоретическим потенциалом разложения. Но на практике внешнее напряжение должно быть несколько больше, чем ЭДС возникшего ГЭ и подбирается практически.
Существует таблица перенапряжений. Перенапряжением выделения водорода называется смещение или сдвиг потенциала выделения водорода в сторону более отрицательных значений при при его выделении на данном материале по сравнению с выделением его на чернёной платине.
33. Электролиз находит применение в очистке сточных вод. Явление электролиза широко применяется в современной промышленности. В частности, электролиз является одним из способов промышленного получения алюминия, водорода, а также гидроксида натрия , хлора, хлорорганических соединений[источник не указан 220 дней], диоксида марганца[1], пероксида водорода. Большое количество металлов извлекаются из руд и подвергаются переработке с помощью электролиза (электроэкстракция, электрорафинирование). Электрохимические процессы широко применяются в различных областях современной техники, в аналитической химии,биохимии и т. д. В химической промышленности электролизом получают хлор и фтор, щелочи, хлораты и перхлораты, надсерную кислоту и персульфаты, химически чистые водород и кислород и т. д. При этом одни вещества получают путем восстановления на катоде (альдегиды, парааминофенол и др.), другие электроокислением на аноде (хлораты, перхлораты, перманганат калия и др.).
Электролиз в гидрометаллургии является одной из стадий переработки металлсодержащего сырья, обеспечивающей получение товарных металлов.
Электролиз может осуществляться с растворимыми анодами - процесс электрорафинирования или с нерастворимыми - процесс электроэкстракции.
Главной задачей при электрорафинировании металлов является обеспечения необходимой чистоты катодного металла при приемлемых энергетических расходах.
В цветной металлургии электролиз используется для извлечения металлов из руд и их очистки. Электролизом расплавленных сред получают алюминий, магний, титан, цирконий, уран, бериллий и др.
Для рафинирования (очистки) металла электролизом из него отливают пластины и помещают их в качестве анодов в электролизер. При пропускании тока металл, подлежащий очистке, подвергается анодному растворению, т. е. переходит в раствор в виде катионов. Затем эти катионы металла разряжаются на катоде, благодаря чему образуется компактный осадок уже чистого металла. Примеси, находящиеся в аноде, либо остаются нерастворимыми, либо переходят в электролит и удаляются.
Гальванотехника – область прикладной электрохимии, занимающаяся процессами нанесения металлических покрытий на поверхность как металлических, так и неметаллических изделий при прохождении постоянного электрического тока через растворы их солей. Гальванотехника пожразделяется на гальваностегию и гальванопластику.
Гальваностегия (от греч.покрывать) – это электроосаждение на поверхность металла другого металла, который прочно связывается (сцепляется) с покрываемым металлом (предметом), служащим катодом электролизера.
Перед покрытием изделия необходимо его поверхность тщательно очистить (обезжирить и протравить), в противном случае металл будет осаждаться неравномерно, а кроме того, сцепление (связь) металла покрытия с поверхностью изделия будет непрочной. Способом гальваностегии можно покрыть деталь тонким слоем золота или серебра, хрома или никеля. С помощью электролиза можно наносить тончайшие металлические покрытия на различных металлических поверхностях. При таком способе нанесения покрытий, деталь используют в качестве катода, помещенного в раствор соли того металла, покрытие из которого необходимо получить. В качестве анода используется пластинка из того же металла.
Гальванопластика– получение путем электролиза точных, легко отделяемых металлических копий относительно значительной толщины с различных как неметаллических, так и металлических предметов, называемых матрицами.
С помощью гальванопластики изготовляют бюсты, статуи и т. д.
Гальванопластика используется для нанесения сравнительно толстых металлических покрытий на другие металлы (например, образование "накладного" слоя никеля, серебра, золота и т. д.).
34. Фарадея законы, основные законы электролиза, отражающие общий закон сохранения вещества в условиях протекания электрохимической реакции. Установлены M. Фарадеем в 1833-34.
Согласно 1-му закону, масса вещества г, прореагировавшего в процессе электролиза, прямо пропорциональна силе тока I и времени электролизаt, то есть количеству пропущенного электричества Q = It(предполагается, что I не зависит от t; в противном случае масса гпропорциональна t1 и t2 - моменты включения и выключения тока).
Согласно 2-му закону, для разных электродных процессов при одинаковом количестве пропущенного электричества Q массы прореагировавших веществ относятся друг к другу так же, как эквиваленты химические этих веществ. Оба закона Фарадея объединяются одним уравнением:
где M - молярная масса вещества, участвующего в электролизе, z - число элементарных зарядов, соответствующее превращению одной молекулы этого вещества, 1/F- коэффициент пропорциональности, общий для всех веществ, F - постоянная Фарадея, равная 96484,56 Кл/моль.
Законы Фарадея законы относятся к числу строгих законов, но в ряде случаев могут наблюдаться кажущиеся отклонения от них, вызываемые следующими причинами:
1) в нестационарных условиях электролиза часть электричества затрачивается на заряжение двойного электрического слоя.
2) если электролит обладает электронной проводимостью (например, раствор металлического Na в жидком аммиаке), то часть тока через электролит переносят электроны, а не ионы, и соответствующее количество электричества не участвует в процессе электролиза;
3) наряду с основным процессом электролиза, например образованием металлического Zn по реакции Zn 2+ + 2е 3O + + 2е = H2 + 2H2O; O2 + 4е + 4H3O + = 6H2O.
Системы, в которых полностью исключены указанные причины кажущихся отклонений от законов Фарадея, получили название кулонометров; их использование позволяет по количеству образовавшихся продуктов электролиза точно определить кол-во пропущенного электричества. В кулонометрах обычно применяют электрохимические реакции Ag + + е = Ag или 3I - = I3 - + 2е.
Законы Фарадея законы сыграли важную роль в понимании природы химической связи и развития атомно-молекулярной теории. Их используют при выводе всех уравнений, описывающих электрохимические превращения веществ на границах раздела проводников 1-го и 2-го рода. Практическое применение законы Фарадея законы находят в кулонометрии, а также при определении выхода реакции по току, то есть отношения теоретического количества электричества, рассчитанного на основе законов Фарадея законы, к количеству электричества, реально затраченному на получение данного вещества в процессе электролиза.
Уравнение Нернста, направление протекания окислительно-восстановительных реакций в растворах и константы их равновесия
Участие электронов в протекании полуреакций кажется естественным только при наличии металлов, в которых существует «электронный газ». Между тем существует огромное число реакций окисления-восстановления, которые протекают в водных растворах между гидратированными ионами или между ионами и молекулами. Более того, эти реакции можно проводить как сумму двух полуреакций, проходящих в полуэлементах-электродах, соединенных в гальванический элемент. Следовательно, и для таких реакций участие в них электронов является физической реальностью.
В качестве примера рассмотрим реакцию
Ее можно реализовать с помощью гальванического элемента, состоящего из двух полуэлементов-электродов (рис. 12.2), в которых протекают полуреакций
Полуреакция окисления иодид-ионов записана упрощенно. В присутствии избытка I" молекулы Ь образуют растворимые в воде анионы I3.
Как очевидно из рис. 12.2, устройство обоих электродов, служащих для раздельного проведения этих полуреакций,
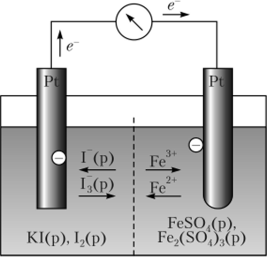
Рис. 12.2. Гальванический элемент, состоящий из двух окислительно-восстановительных электродов почти такое же, как и у водородного электрода. В водные растворы погружены платиновые пластинки, которые служат в качестве сборника электронов в левом нолуэлементе и источника электронов в правом.
Следовательно, реакции окисления-восстановления, проходящие в растворах, можно рассматривать как суммы или разности полуреакций, имеющих совершенно определенные значения Е° (см. табл. 12.2).
Для установления количественной связи между ЭДС гальванического элемента и константой равновесия протекающей в нем реакции служит уравнение Нернста. Оно выражает зависимость электродного потенциала от активностей потенциал определяющих веществ полуреакций:
где Е — окислительно-восстановительный электродный потенциал при произвольных условиях; Е° — стандартный электродный потенциал (табличная величина); R — универсальная газовая постоянная; Т — температура; п — число электронов, принимаемых окисленной формой при превращении ее в восстановленную форму; F — постоянная Фарадея; Пяокисл — произведение активностей окисленной формы и всех ионов и молекул, записываемых в уравнении вместе с этой формой в левой части полуреакции; Павосст — произведение активностей восстановленной формы и всех ионов и молекул, записываемых в уравнении полуреакции вместе с этой формой в правой части полуреакции. Активности берутся в степенях, равных стехиометрическим коэффициентам перед формулами компонентов.
После подстановки числовых значений констант /?, F и Т= 298,15 К и в результате замены натурального логарифма на десятичный уравнение Нернста принимает вид
Например, для полуреакции
Если учесть, что в водных растворах активность воды равна единице, то уравнение (12.4) приобретает следующий вид:
Использование уравнения Нернста позволяет вычислять ЭДС гальванического элемента не только в стандартных условиях в соответствии с уравнением (12.1), но и тогда, когда активности веществ, оказывающих влияние на электродный потенциал, не равны единице.
Например, ЭДС гальванического элемента, изображенного на рис. 12.2, можно вычислить как разность электродного потенциала ?Ve 3+ /Fe 2+ электрода, в котором окисленной формой являются катионы Fe , а восстановленной — катионы Fe 2+ , и электродного потенциала Ещг электрода, в котором окисленной формой являются молекулы 12, а восстановленной — иодид-ионы Г:
После подстановки в уравнение (12.6) выражений, полученных на основании уравнения Нернста (12.2) и иллюстрирующих зависимость электродных потенциалов от активностей потенциалопределяющих частиц, получаем
Значение AE° = 0,771 - 0,536 = 0,235 B.
При достижении состояния равновесия активности реагентов и продуктов реакции приобретут равновесные значения, а ЭДС гальванического элемента станет равной нулю:
Выражение, стоящее под знаком логарифма, при этом станет равным величине, обратной константе равновесия:
В общем случае, когда в реакции принимает участие п электронов, справедливо уравнение
из которого очевидно, что константа равновесия может быть больше единицы только при АЕ° > 0. Иными словами,
реакции окисления-восстановления протекают слева направо только тогда, когда ЭДС гальванического элемента, образованного из полу элементов-электродов, является положительной величиной.
Такой гальванический элемент может совершать работу. Это заключение находится в соответствии со вторым началом термодинамики, согласно которому самопроизвольно протекают лишь реакции, имеющие отрицательные AG. Из уравнения (5.15) получаем общую связь между ЭДС (АЕ°) гальванических элементов, АСрсакции и константой равновесия К:
Результаты расчета AGp^^ и констант равновесия, полученные при использовании стандартных электродных потенциалов, применимы не только к процессам в гальванических элементах, но и к окислительно-восстановительным реакциям, протекающим при непосредственном смешении растворов.
Уравнение Нернста
Изменение условий, в которых проходит полуреакция, приводит к изменению величины электродного потенциала. Влияние активности компонентов, участвующих в этом процессе, и температуры на величину потенциала описывается уравнением Нернста:
где Eox/Red — величина реального электродного потенциала (т.е. потенциала при активностях компонентов, отличных от стандартных); Eox/Red — величина стандартного электродного потенциала; R — универсальная газовая постоянная; п — число электронов, участвующих в полуреакции; F — число Фарадея; а0х, aRed — активности окисленной и восстановленной форм соответственно (в степенях, равных стехиометрическим коэффициентам).
Если объединить постоянные величины в одну константу, а натуральный логарифм заменить десятичным, то при Т = 298 К уравнение (14.2) будет иметь следующий вид:
Например, для приведенной ниже полуреакции восстановления дихромат-иона, протекающей в кислой среде, уравнение (14.3) будет выглядеть так:
Активность воды в выражение, стоящее после знака логарифма, не входит, так как вода в данном случае является растворителем и ее активность принимается равной 1 (см. гл. 6). Из уравнения Нернста можно исключить компоненты, находящиеся в стандартном состоянии.

Нернст (Nernst) Герман Вальтер
Немецкий физик и химик (он считал себя физиком, занимающимся химией). Родился в г. Бризе- не (ныне Вомбжезьно, Польша). В 1883-1887 гг. учился в университетах Цюриха, Берлина, Граца и Вюрцбурга. Затем работал в Лейпцигском, Геттингенском и Берлинском университетах.
Фундаментальный закон, известный как уравнение Нернста, был открыт им в 25-летнем возрасте. Благодаря этой работе молодой ученый получил всемирное признание. В 1890-1891 гг. В. Нернст занимался изучением веществ, которые при рас-
творении в жидкостях не смешиваются друг с другом, и предложил закон распределения. В 1905 г. он сформулировал свою «тепловую теорему», известную теперь как третье начало термодинамики. В 1912 г. обосновал недостижимость абсолютного нуля. В 1921 г. ученому была вручена Нобелевская премия по химии, присужденная в 1920 г. в знак признания его работ по термодинамике. Интересно, что в школьные годы В. Нернст хотел стать поэтом, но учитель химии пробудил в нем интерес к естественным наукам.
Во всех рассмотренных ранее видах равновесий мы сталкивались с условными концентрационными константами равновесия, которые очень удобно применять для расчетов в тех случаях, когда в растворе протекают различные побочные реакции. Среди электродных потенциалов также существуют такие константы, именуемые формальными электродными потенциалами.
Зависимость между общей концентрацией вещества в растворе и активностью его формы, участвующей в рассматриваемом окислительно-восстановительном равновесии, имеет такой вид:
Объединим выражения (14.3) и (14.4):
После математических преобразований выражения (14.5) получаем:
Сумма первых трех членов в уравнении (14.6), выделенная полужирным шрифтом, для конкретных условий, в которых протекает полуреакция (например, определенные ионная сила, pH и концентрация лиганда или иона-осадителя), представляет собой постоянную величину и называется формальным электродным потенциалом полуреакции.
Формальный электродный потенциал ?ох Red — эт0 потенциал полуреакции, измеренный при условии, что общие концентрации окисленной и восстановленной форм равны 1 моль/л, а концентрации посторонних ионов известны.
Величина формального потенциала зависит от ионной силы раствора, а также природы и концентрации посторонних электролитов. По величине формального потенциала в той или иной среде можно судить о протекании процессов комплексообразова- ния, выпадения осадков и др. Например, стандартный потенциал .Ерез+/Fe 2+ = +0,771 В. Формальный потенциал для этой же реакции в 1 М H2S04 равен +0,68 В, в 1 М К2С204 (pH 5) он составляет всего +0,01 В, в 10 М NaOH равен -0,68 В. Уменьшение потенциала связано с процессами комплексообразования в присутствии данных фоновых электролитов, причем окисленная форма образует более прочные комплексы, чем восстановленная.
Читайте также:
