Моделирование функций нервной системы

Разработка вопросов теории и практики применения искусственных самоорганизующихся систем, или "обучающихся автоматов", обусловила повышенный интерес специалистов точных наук и техники к проблемам обучения человека и животных, количественному анализу структуры и функций нервной системы.

Однако огромный материал, накопленный физиологией в. н. д., получен преимущественно в упрощенных частных условиях, и поэтому многие выводы этих исследований не могут быть непосредственно использованы для сопоставления с результатами, полученными на описанных выше моделях. Не существует, например, сопоставимых количественных критериев для оценки оптимальности поведенческих реакций организма, эффективности переработки информации в различных отделах нервной системы и некоторых других показателей, необходимых для оценки возможностей мозга как сложной управляющей системы в сравнении с автоматическими устройствами.

Теория обучения автоматов охватывает широкий круг вопросов, который имеет отношение по крайней мере к следующим этапам условнорефлекторного поведения: 1) активный поиск и различение каждого из условных и безусловных раздражителей; 2) определение статистической структуры безусловных раздражителей во времени и пространстве, а также по отношению к окружающим предметам или сигналам (условным раздражителям); 3) различение внутренних состояний отдельных элементов организма (автомата) и их частных задач, определяемых текущим моментом и прошлым опытом; 4) формирование и выполнение реакции, 5) контроль адекватности (эффективности) реакции, и т. д.

Понятно, что рассмотренные в предыдущих разделах модели нейронов и самоорганизующихся систем - логические сети, конечные автоматы - являются лишь весьма отдаленными аналогами структуры или функций нервной системы. Однако ценность моделей заключается не только в наиболее близкой имитации работы мозга, но и в возможности сравнить с тем, как он мог бы или как он не мог бы работать. Здесь вполне уместно привести слова И. М. Сеченова (1952): "Мысль о машинности мозга при каких бы то ни было условиях для всякого натуралиста клад. Он в свою жизнь видел столько разнообразных причудливых машин, начиная от простого винта до тех сложных механизмов, которые все более заменяют собой человека в деле физического труда, он столько вдумывался в эти механизмы, что если поставить перед таким натуралистом новую для него машину, закрыть от его глаз ее внутренности, показать лишь начало и конец ее деятельности, то он составит приблизительно верное понятие и об устройстве этой машины и об ее действии". Успехи современной электроники и развитие кибернетики позволяют создавать машины, заменяющих человека и в деле умственного труда, и нужно полагать, что эти устройства для изучения мозга окажутся еще более полезными, чем машины времен И. М. Сеченова.

Самое главное, что дали нам кибернетические представления о деятельности мозга, - это то, что важнейшая функция мозга - эффективное, целенаправленное управление и регуляция внутренних состояний в изменяющейся внешней среде - доступна для функционального моделирования, и что деятельность мозга подчинена тем же ограничениям, которые установлены теорией информации. Так, например, оптимальное приспособление живого организма, заключающееся в поддержании постоянства его основных параметров в допустимых пределах при наличии внешних изменений и вредных воздействий, гомологично с коррекцией шумов в канале связи.

По известной теореме следует, что для исправления ошибок путем некоторого числа выборов через корректирующий канал должно пройти соответствующее данному числу выборов количество информации. И мозг в этом случае действует так же, т. е. не может выполнить эти функции, пока не примет и не передаст необходимого количества информации (если не верить в чудеса). Данное обстоятельство, конечно, не следует понимать пессимистически, ибо таким же образом открытие закона сохранения энергии положило конец попыткам построить вечный двигатель, но оно же явилось началом бурного развития и успехов техники в новом направлении. Зная ограничения, которым подчиняется работа мозга, мы сможем глубже понять его механизмы и детали строения.

Вообще при изучении сложных систем, имеющих иерархию уровней ее организации или форм движения материи, следует всегда иметь в виду высшие функции системы или направления развития, которым подчиняются детали ее структуры. Поскольку можно предположить, что мозг является оптимальным регулятором, то целесообразно ознакомиться со структурами современных систем автоматического управления. Оставляя в стороне простые случаи, когда в системе имеется полная информация о состоянии объекта и возмущающих воздействиях, рассмотрим систему с неполной информацией и автоматическим поиском (Фельдбаум, 1964). Основой решения какой-либо задачи в неопределенной ситуации является метод активного поиска (Бернштейн, 1962; Гельфанд и соавт., 1962). Этот метод состоит в пробах различных путей и способов решения, без гарантии успеха. В простейшем случае (или когда имеется очень мало информации) используется метод слепого или случайного поиска (выбора), или известный в биологии метод "проб и ошибок" (Эшби, 1956). В последнее время большее внимание уделяется методам эвристического программирования, где используются психологические данные о действии человека по достижению какой-либо цели (Миллер, Галантер, Прибрам, 1959). Прежде всего выбирается (на основе прошлого опыта) зарекомендовавшая себя стратегия, которая проверяется в действии, и в случае неудачи вносится коррекция, выдвигается новая гипотеза о возможных путях решения задачи, и так далее до получения успеха (хотя и этот метод не дает полной гарантии успеха).

Рассмотрим схему автоматической оптимизации (рис. 93). Управляемый объект В находится под воздействием управляющего сигнала u от управляющего устройства А₁ и случайной помехи z, медленно изменяющейся во времени. Выходная реакция должна повторять закон действия х′ задающего сигнала, причем во всех каналах связи имеются помехи, искажающие передаваемую информацию. Автоматический оптимизатор А₂ воспринимает значения критерия оптимальности О и ограничений H_i, вычисленных устройством С на основании сравнения задающего и выходного сигналов. Затем, действуя через управляющее устройство на объект, автоматический оптимизатор изменяет параметры А₁ в нужном направлении, в зависимости от реакции объекта, для повышения критерия оптимальности.

Рис. 93. Структурная схема оптимального управления с автоматическим поиском. A₁- управляющее устройство; В - управляемый объект; С - вычислительное устройство; А₂ - автоматический оптимизатор (прерывистой линией очерчен объект оптимизации). Объяснения в тексте

Вообще обычная система автоматического регулирования состоит из следующих основных элементов: входное и выходное устройства, переключательный блок (управления), цепи обратной связи и органы сравнения прямого и обратного сигнала, моделирующее устройство (в схемах управления по модели) и устройство памяти. Аналогичные структуры можно найти и в нервной системе (Поляков, 1964; Соколов, 1964б). На рис. 94 и 95 показаны схемы нейронной организации ориентировочного и условного рефлексов. Принципиальное отличие этой структуры заключается в пластичности ее элементов.

Рис. 94. Структурная схема ориентировочного и условного рефлексов. (Соколов, 1964б)

Рис. 95. Схема нейронной организации ориентировочного и условного рефлексов. (Соколов, 1964б)

По-видимому, в биологических системах управления и регулирования с целью наилучшей выживаемости в условиях изменяющихся в широких диапазонах влияний внешней среды и активной борьбы за существование в процессе эволюции вырабатывались очень гибкие, разнообразные механизмы перестройки не только в количественном (саморегуляция), но и в качественном (самоорганизация) аспектах. Поэтому можно предположить, что нервная система и ее элементы могут изменять свои свойства под влиянием биологически значимых (экологически адекватных) раздражителей внешней среды и внутренних состояний организма постольку, поскольку это необходимо для наилучшей выживаемости. В этом смысле быстрота реакций может выигрываться за счет точности и наоборот, а вычислительные функции могут "обмениваться" с логическими и т. д. Так, например, можно полагать, что нейрон или элемент такой информационной системы имеет весьма сложный алгоритм преобразования выходного сигнала как по самой функции входа, так и по ее интегралу и производной во времени и в пространстве для оптимального выполнения текущей задачи данного нейрона в составе целостной деятельности нервной системы. Этот, беспорядочный на первый взгляд, смешанный код оказывается наиболее эффективным при передаче и переработке биологически важной информации в прошлом, в настоящий момент и в будущем. Можно думать, что в нервной системе производится поэтапная выработка реакций с последовательными приближениями точности. Такой способ действия позволяет в общих чертах сформулировать реакции почти мгновенно и затем по мере необходимости их уточнять и детализировать, что дает возможность обеспечить гибкий компромисс между правильностью действия и постоянной готовностью к любым неожиданным раздражениям.

Можно предположить, что саморегуляция и самоуправление организма во внешней среде выполняются сложной иерархией управляющих систем на основе физических, логических, семантических и прагматических принципов функционирования. При этом последние являются высшими и управляют низшими, в соответствии с программой деятельности целого организма (Виннер, 1948; Эшби, 1956; Буллок, 1964; Поляков, 1964).

Казалось бы, можно построить теорию функционирования мозга, даже не зная внутреннего строения отдельных нейронов. Однако мы еще слишком мало знаем и об общих или основных принципах взаимодействия их. Отдельно исследовали электрические, химические и различные биофизические параметры отдельных нервных клеток и пытаются экспериментировать с группами клеток, контролируя правильность анализа тем, что объяснения работы и реакций ансамблей клеток не должны противоречить принципам, полученным при исследовании отдельных единиц.

Последние несколько десятилетий характеризуются представлениями о нервной системе как о некоторой весьма сложной телефонной сети с автоматическим коммутатором или обычной электронной вычислительной машине, в которой определенные виды сигналов или взаимодействий передаются по определенным каналам связи и поэтому могут быть точно локализованы в каждый данный момент. Однако в настоящее время все чаще подчеркивается существенное отличие структуры реальной нервной системы от обычной электрической сети с "сосредоточенными постоянными". Предполагается, что все основные функции мозга - способность к обмену веществ, энергией и информацией, память, переключения, классификация различения и тому подобное распределены по миллионам клеток, одновременно участвующих во множестве других системных процессов и составляющих статистическую систему переменных времени, места и состояния (мозаику возбуждений и задерживаний по И. П. Павлову). Такое представление отличается от структуры логической сети из дискретных элементов, и пока еще нет удовлетворительных моделей такого типа, но разработка отдельных элементов для этой цели продолжается.

Особенный интерес в нейрофизиологии и нейрокибернетике в настоящее время представляют различные модели и гипотезы о материальных носителях памяти, или следов возбуждений в нервной системе, на которых могут быть построены правдоподобные модели временной связи. Многочисленными исследователями разрабатывались модели памяти как циклической активности нервных импульсов в замкнутых нейронных контурах. Успехи математической модели взаимосвязи между внутриклеточными и внеклеточными значениями потенциалов действия (Ролл, 1961, и др.) дают основание надеяться, что эта модель может быть использована и при исследовании иных проблем нейрофизиологии, представляющих значительный интерес. Например, найденное различие между вялой реакцией на периферическую дендритную синаптическую активность и значительно более быстрой реакцией на синаптическую активность в соме (и стволе дендрита) позволяет провести обобщение ранее предложенных рефлекторных моделей типа "вход-выход". Это различие между синаптической активностью в дендритах и соме может оказаться также очень важным при рассмотрении проблемы нейронных взаимодействий в больших популяциях. Данный эффект должен быть учтен в коэффициентах, выражающих запаздывающую связь.

Другое направление в исследовании следов возбуждения в нервной системе относится к поискам физиологических механизмов адаптации, постетанической потенциации, роста отдельных элементов нейронов, проявляющихся в ходе "проторения" пути при выработке условного рефлекса.

Кибернетика и нервная система

Многое в работе нервной системы человека до сих пор непонятно учёным. Тем не менее общие закономерности управления, установленные кибернетикой, справедливы и для неё. Кибернетика разрабатывает математические приёмы, позволяющие на основе внешних данных судить о поломке математической машины. Врач встречается с аналогичной задачей. На основе внешних признаков требуется установить характер заболевания. Основываясь на кибернетике, медицина использует разработанные ею методы для решения и этой задачи. Исследуя закономерности управления, общие для механизма и нервной системы, кибернетика должна оперировать понятиями, применимыми к тому и другому.

Как мозг, так и машина состоят из определённых элементов, которые в своей совокупности образуют единое целое – систему. Это можно сказать как о всём мире в целом, так и об отдельных его частях.

Искусственные управляющие устройства так же как мозг человека, относят к одному и тому же классу самоуправляющихся систем. Все такого рода самоуправляющиеся системы называют кибернетическими.

Каждая система связана с внешним миром, который так или иначе влияет на неё и, в свою очередь, подвергается воздействиям с её стороны. Ту часть системы, которая воспринимает воздействие извне, называют входом, а ту, которой система действует на другие системы, – выход ом.

В одной системе может быть один, два или несколько входов и выходов. Регулятор Уатта, например, имеет один вход и один выход. На входе происходит изменение давления, на выходе – открывание или закрывание клапана. Человек как система имеет множество входов и выходов в виде нервных клеток, воспринимающих внешние воздействия и реагирующих на них.

Всякая кибернетическая система, как указывалось выше, является самоуправляющейся.

Но управление не сводится просто к передаче информации от управляющей части системы к исполнительному органу. Этот процесс гораздо сложнее.

Дело в том, что на исполнительный орган влияет не только управляющая система. Он подвержен непрерывным воздействиям окружающей среды, которые часто препятствуют исполнению приказов, полученных от управляющего центра. Например, корабль может отклониться от прямого пути под влиянием неожиданно поднявшегося ветра. Что предпринять в этом случае? Очевидно, нужно повернуть руль корабля так, чтобы он мог держать прежний курс. Противодействие случайным внешним влияниям – общий закон всякого регулирования.

Самый надёжный способ противодействовать внешним возмущениям – это сделать так, чтобы всякое отклонение фактического поведения от заданного, независимо от того, чем оно обусловлено, вызывало определённую ответную реакцию, направленную на ликвидацию этого отклонения. В таком случае не нужно изучать его причины, определять силу ветра, направление течения и т.д.; заданное направление поддерживается автоматически. Такой способ управления был найден. Нужно, чтобы кроме прямой связи устройства управления с исполнительной системой была обеспечена связь выхода исполнительной системы с входом управляющей (см. рис. 65). Эту дополнительную связь называют обратной.

Примеры обратной связи мы уже видели выше. Обратная связь, вызывающая в результате своего действия ослабление внешнего влияния, носит название отрицательной обратной связи. Принцип регулирования на основе отрицательной обратной связи находит применение в любой управляемой системе, будь то кибернетическая машина или живой организм.

Положение о том, что регулирование в живом организме, в том числе в центральной нервной системе человека, происходит на основе отрицательной обратной связи, иногда называют основной гипотезой кибернетики.

Рис. 65. Обратная связь

Общий для кибернетических машин и живых организмов принцип обратной связи неслучаен. Ведь и те и другие вынуждены действовать в постоянно меняющихся условиях, поэтому реакции, вырабатываемые у них, должны отличаться разнообразием. Но для этого необходимо, чтобы из рабочего органа в центральную систему поступали соответствующие сигналы. Обратная связь лежит в основе восстановления и перестройки функций центральной нервной системы.

Прежде чем говорить о возможностях моделирования мозга как управляющего центра разумных действий, нужно представить себе элементы сложнейшей нервной системы – нейроны – и попытаться создать их модель.

Значительная или даже, пожалуй, основная часть нынешних исследовательских работ по бионике посвящена созданию аналогов биологического нейрона – нервной клетки – основного элемента нервной системы. Конечная цель этих работ – создание систем, предназначенных для накопления, обработки и передачи большого количества информации, электронных машин, способных решать любые сложные задачи без предварительного программирования, различных самообучающихся, адаптивных (самоприспосабливающихся, самоорганизующихся устройств), обладающих малыми габаритами и высокой надёжностью машин. Иными словами, речь идёт о создании широкого комплекса автоматических систем, работающих по тем же принципам.

Что такое нейрон? Это нервная клетка человеческого мозга (рис. 66). В мозге человека их около 15 миллиардов, и мы о них очень мало знаем. Нейрон был и остаётся величайшей загадкой. Каждый нейрон снабжён выходным каналом – аксоном. По нему передаётся возбуждение к какому – либо органу. Например, тело нервной клетки находится в спинном мозге, а её аксон достигает мышц пальцев ноги. Если бы мы захотели сделать в масштабе большую модель аксона, хотя бы в виде шланга диаметром 4 см, то его длина оказалась бы более 16 км. Другие отростки нейрона – дендриты – являются входами в тело нервной клетки.

Аксоны и дендриты различных клеток переплетаются и соединяются во многих (до тысячи) контактных точках. Через эти контакты – синапсы – может передаваться возбуждение от аксона одного нейрона к дендриту другого.

Для создания моделей нейрона применяют главным образом метод физического моделирования. Это естественно: ведь инженеры стремятся разработать элементы для электронных или иных вычислительных машин будущего. Конечно, это должно быть вполне реальное yc тройство, как можно белее компактное и дешёвое. Методом математического моделирования пользуются главным образом при моделировании нейронных сетей.

Рис. 67. Модель нейрона Мак-Каллока и Питтса

Три последних положения лишь частично отражают реальные свойства нейрона. Дело в том, что эта модель является математической абстракцией, предназначенной для моделирования нейронных сетей на цифровых вычислительных машинах. Электронные модели нейрона гораздо точнее копируют его свойства.

Для имитации нейронов применяют магнитные ферритовые магнитопроводы, специальные генераторы и другие устройства. Модель нейрона Мак – Каллока и Питтса с мультивибратором показана на рис. 67. Она позволяет воспроизвести многие характеристики нейрона, кроме его способности к адаптации, т. е. к изменению порога срабатывания в зависимости от уровня входных сигналов. Следует иметь в виду, что модель Мак – Каллока и Питтса сильно упрощена. Биологический нейрон значительно сложнее.

Решение логических задач

Важнейшим практическим результатом кибернетики является использование знаний о работе нервной системы животных и человека для конструирования машин, способных выполнять некоторые их функции.

Рис. 68. Логические элементы И, ИЛИ, НЕ

Современная символическая логика установила, что многие из них можно выразить тремя логическими функциями: НЕ, И, ИЛИ, т. е. отрицание, конъюнкция и дизъюнкция. Поскольку перед машиной ставят задачу осуществления действий, аналогичных действиям человека, его рассуждениям, она должна уметь отрицать, соединять и разделять.

Проиллюстрируем основные операции алгебры логики логическими схемами (рис. 68). Например: устройство И – лампа загорится тогда, когда будут замкнуты оба ключа А и В; устройство ИЛИ – лампа загорится тогда, когда замкнут ключ А или В; устройство НЕ – лампа загорится при каком угодно положении ключа, только не А. Комбинируя эти и им подобные устройства конструкции, получают вычислительные машины, способные решать очень сложные логические задачи.

Если в релейных машинах роль ключа играли электромеханические реле, то в электронных эта роль была поручена сначала электровакуумным приборам – радиолампам, а затем на смену им пришли транзисторы. Это позволило уменьшить размеры машин, повысить их быстродействие. Именно бурное развитие электроники вызвало быструю смену поколений ЭВМ и расширило их возможности.

Но прежде чем говорить о поколениях ЭВМ, полезно вспомнить, что такое электронные полупроводниковые элементы и какова история их появления.

Транзисторы положили начало новой области техники – микроэлектроники. На их основе созданы интегральные микросхемы, и в частности, цифровые. Таким образом, конструкторы получили в своё распоряжение уникальную элементную базу, позволившую создать исключительные по быстродействию и возможностям целые поколения ЭВМ.

Мы узнали, как использовать кибернетику для конструирования думающих машин, заменяющих человека в его логической функции. Но. вскрывая то общее, что имеется у живого организма и машины, кибернетика не ограничивается мыслительной деятельностью человека. Она изучает все особенности поведения живых существ, которые могут быть воспроизведены в машине. И используется эта наука для моделировання не только мышления человека, но и всех других функций нервной системы.

Простейшие автоматические устройства действуют строго по заданной программе. Их поведение не меняется в зависимости от окружающих условий – они не приобретают опыта. Естественно, возникает вопрос: нельзя ли такую особенность регулирования живых ортанизмов. как умение приспосабливаться к среде, придать машине?

Как же работает белка? Большая пустая комната освещена лампами накаливания. По полу в беспорядке разбросаны белые шарики. В одном из углов лежит металлический лист, освещённый люминесцентной лампой, – это гнездо белки. Белка наугад ищет, пока в поле зрения её фотоэлементов не попадёт белый шарик. Тогда она направляется к нему, раздвигает лапки, останавливается и сдвигает их, захватывая шарик. Язычком, находящимся между лапками, белка обнаруживает шарик. Затем она поворачивается и ищет гнездо. Поскольку оно освещено мигающим светом люминесцентной лампы (в отличие от непрерывного света ламп накаливания), электрический фильтр позволяет ей распознать направление. Белка направляется к гнезду, заползает на металлический лист и останавливается на нём, так как замыкание цепи между листом и её металлическим хвостиком даёт знать, что она дома. Белка раздвигает лапки, выбрасывая шарик, и снова направляется на поиск следующего.

Простейшие модели с использованием логических устройств

Как заставить модель обходить, не задевая встречающиеся на пути предметы? Сделать в домашних условиях локатор сложно, да он и не нужен. Глазами автомобиля или робота могут быть фотодатчики. Свет фар, отражённый от преграды и принятый фото датчиками, расскажет логическому устройству о ситуации на дороге. Логическое устройство примет нужное решение и отдаст ту или иную команду исполнительным реле: включить указатель поворота и повернуть направо или налево; продолжить путь по прямой; включить предупреждающие красные фонари, звуковой сигнал или заднюю фару с фотодатчиком и двигаться назад, если оба передних датчика зафиксировали препятствие.

Нейроны

Прежде чем говорить о возможностях моделирования мозга как управляющего центра разумных действий, нужно представить себе элементы сложнейшей нервной системы - нейроны и попытаться создать их модели.

Значительная или даже, пожалуй, основная часть ведущихся ныне исследовательских работ по бионике посвящена созданию аналогов биологического нейрона - нервной клетки, являющейся основным элементом нервной системы.

Конечная цель этих работ - создание систем, предназначенных для накопления, обработки и передачи большого количества информации, электронных машин, способных решать любые сложные задачи без предварительного программирования, различных самообучающихся, адаптивных (самоприспосабливающихся, самоорганизующихся устройств), обладающих малыми габаритами и высокой надежностью. Иными словами, речь идет о создании широкого комплекса автоматических систем, функционирующих по принципу, аналогичному законам деятельности и принципам организации живого мозга.

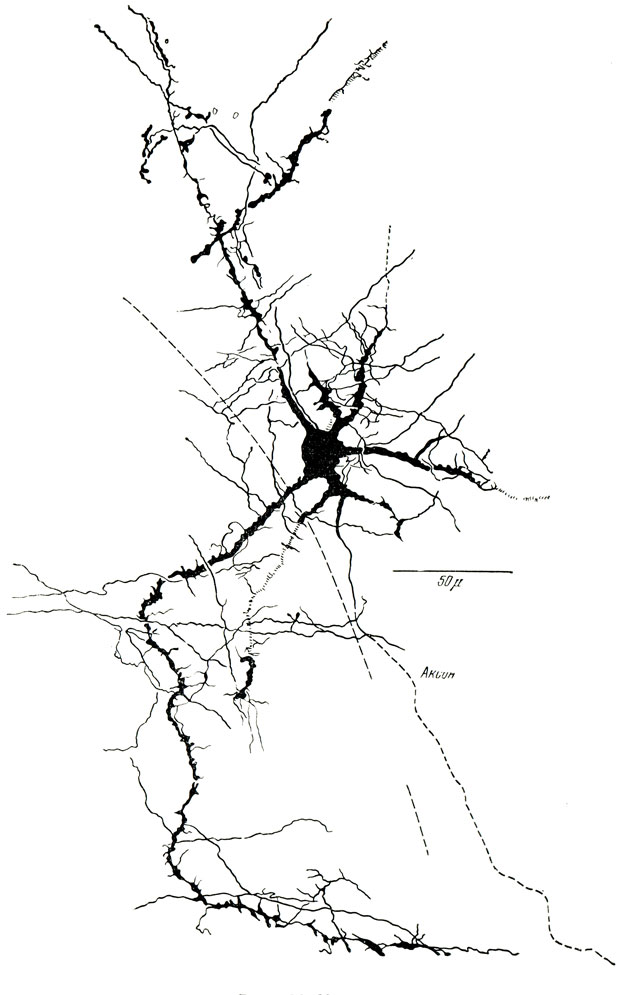
Рис. 90. Нейрон

Что такое нейрон? Это нервная клетка человеческого мозга (рис. 90). В мозгу человека их около 15 млрд., и мы о них почти ничего не знаем. Нейрон был и остается величайшей загадкой. Трудно описать необычную сложность нервной системы человека. Каждый нейрон снабжен выходным каналом - аксоном. По нему передается возбуждение к какому-либо органу. Например, тело нервной клетки находится в спинном мозге, а ее аксон достигает мышц пальцев ноги. Если бы мы захотели сделать большую модель аксона, хотя бы в виде садового шланга (диаметром 4 см), то его длина оказалась бы больше 16 км. Другие отростки нейрона - дендриты - являются входом в тело нервной клетки. Аксоны и дендриты различных клеток переплетаются и соединяются во многих (до тысячи) контактных точках. Через эти контакты - синапсы - может передаваться возбуждение от аксона одного нейрона к дендриту другого.

Нейроны плотно окружены так называемыми глиальными клетками, которых раз в десять больше, чем нейронов. Раньше считали, что эти клетки лишь "закрепляют" нейроны на месте или помогают им питаться. Однако последние исследования показали: клетки глии активно участвуют в проведении нервных импульсов, в формировании реакций и некоторых проявлениях функций памяти. Похоже, что разум равномерно "размазан" по всем структурам нервной системы.

Нейрон как электрическая система - преобразователь импульсов (рис. 91). В спокойном состоянии он имеет по отношению к окружающей среде небольшое отрицательное напряжение, примерно 70 мВ, этот потенциал может меняться до +10 мВ. Как только потенциал нейрона достигает +10 мВ, начинает действовать своего рода обратная связь, которая самостоятельно приводит систему в исходное состояние и заставляет напряжение снизиться до потенциала покоя. При этом на выходе нейрона возникает импульс. В течение этого времени занятости, которое длится около 1 мкс, клетка не чувствительна к внешним воздействиям. Этот принцип имеет далеко идущие последствия.

Для возбуждения нервной клетки недостаточно импульса, приходящего только к одному из синапсов клетки, необходимо почти одновременное воздействие импульсов на несколько синапсов дендритов клетки. Если отдельные поступающие импульсы не достигают порогового значения, то в результате совместного воздействия многих импульсов (если они поступают одновременно) на выходе нейрона появится импульс. Это принцип действия схемы И в ЭВМ (далее о схемах И и ИЛИ рассказывается более подробно). Таким образом, нервная клетка является своего рода цифровой системой, подобной той, которой мы пользуемся в ЭВМ.

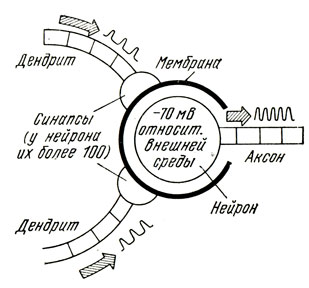
Рис. 91. Нейрон как электрическая система

Если на многие отдельные входы нейрона подать несколько смещенных по времени групп импульсов, то они с помощью нейрона автоматически складываются в пачки. Этот процесс похож на своего рода осмысливание. Убедимся в этом на примере глаза.

Ученые, занимающиеся анатомией и развитием глаза, показали, что сетчатка, в сущности, не что иное, как часть самого мозга: при развитии зародыша часть мозга выносится вперед, из нее назад вырастают длинные волокна, которые связывают ее с остальным мозгом. По своей организации сетчатка весьма похожа на мозг. По этому поводу кто-то прекрасно сказал, что это "мозг выдумал, как ему взглянуть на мир". Глаза - это кусочки мозга, которыми он, так сказать, "касается света", внешнего мира. В трех слоях клеток глаза проводится анализ, результаты которого передаются по зрительному нерву в мозг.

Интересные эксперименты, подтверждающие это, были проведены с глазом краба-мечехвоста. Его глаз содержит около тысячи светочувствительных элеменов - омматидиев.

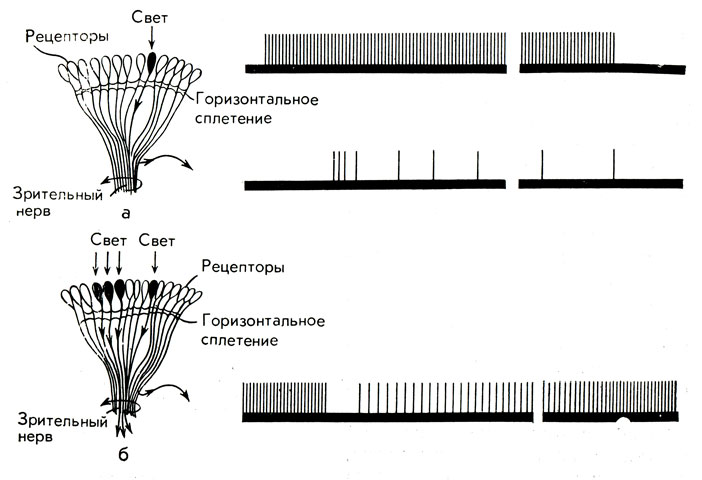
Рис. 92. Импульсы омматидия

Если на зрительный нерв краба наложить небольшие электроды и осветить с помощью линз только один омматидий (рис. 92), то на осциллографе мы увидим серию частых импульсов. Через некоторое мгновение частота их становится меньшей (импульсы идут реже (рис. 92, а). Если свет направить на какой-либо другой омматидий, то импульсов не будет.

Если же мы осветим первый омматидий и получим те же импульсы, а затем направим свет на соседний, то на короткое время импульсы прекращаются, а затем "бегут" снова, но с заметно меньшей частотой (рис. 92, б). Оказывается, импульсы, возникающие во втором омматидии, затормаживают импульсы первого.

Другими словами, хотя каждый нерв и несет информацию о своем омматидии, количество этой информации подавляется сигналами от другого омматидия. Например, когда более или менее равномерно освещен весь глаз, то сигнал, пришедший от любого отдельного омматидия, будет относительно слабым, ибо он подавлен множеством других сигналов. Торможение, как говорят, аддитивно (торможения складываются), т. е. если мы осветим несколько соседних омматидиев, торможение будет очень сильным. Торможение оказывается большим, если омматидии расположены близко, и оно практически сводится к нулю, если омматидии удалены друг от друга. Это первый пример, когда информация от различных частей глаза перерабатывается в нем самом.

Небольшое отвлечение сделано нами и для того, чтобы показать, что нервные импульсы можно наблюдать на экранах осциллографов. Их природу и поведение ученые исследуют экспериментально. Это пока лишь первые, самые робкие шаги в неизведанную интереснейшую область изучения природы мышления.

К сказанному о свойствах нейрона как цифрового коммутационного элемента можно добавить следующее: он может хорошо осуществлять аналоговые вычислительные операции, преобразовывать интенсивность в последовательность импульсов, складывать и умножать.

Нейрон, как уже отмечалось, преобразователь с двоичным выходом, т. е. с отсутствием или наличием сигнала. На нейрон биологического организма может подаваться возбуждающий или тормозящий импульс. Первый вызывает "срабатывание" нейрона, если энергия, накапливаемая нейроном за определенный отрезок времени, превысит некоторое, как говорят, пороговое значение. Если амплитуда импульса мала, нейрон не "сработает". Но если последовательно действует несколько слабых сигналов, энергия которых в общей сложности превышает пороговое значение, то нейрон "срабатывает". Это означает, что он обладает свойством временного и пространственного суммирования. На выходе нейрона образуются импульсы определенной амплитуды и длительности.

Последовательным или временным суммированием называют такое возбуждение нейрона, когда раздражения, меньшие пороговых, следуют через достаточно короткие промежутки времени. Пространственное суммирование состоит в одновременном подведении к двум или нескольким синапсам отдельных раздражений, более слабых, чем пороговые значения. В сумме они могут вызвать возбуждение нейрона.

Модель нейрона изображена на рис. 93. У нее множество входов, куда поступают сигналы р₁, р₂, . р_n, которые действуют через синаптические контакты s₁, s₂, . . ., s_n. В этих контактах поступающий сигнал задерживается на время, в течение которого выделяется особое вещество, повышающее возбудимость нейрона и облегчающее реакцию клетки на последующие импульсы.

Воздействие на тело нейрона определяется суммой воздействий от всех входов и сигналами, действовавшими до этого. Нейрон срабатывает, если воздействие превысит пороговое значение К. Тогда на выход нейрона поступает стандартный сигнал Р.

Мы уже отмечали, что сразу же после воздействия возбуждающего импульса пороговый уровень нейрона возрастает. Значит, никакой вновь приходящий сигнал не заставит его "срабатывать". Такое состояние сохраняется обычно в течение нескольких миллисекунд, затем пороговый уровень снижается. Что касается тормозящего импульса, то он представляет собой запретный сигнал, делающий невозможным "срабатывание" нейрона от импульсов других входов.

Для моделирования нейронов применяется главным образом метод физического моделирования. Это естественно: создавая такую модель, инженеры стремятся создать элементы для электронных или иных вычислительных машин будущего. Конечно, это должно быть вполне реальное устройство, по возможности, более компактное и дешевое. Метод математического моделирования применяется главным образом при моделировании нейронных сетей.

Прежде чем работать над моделью, необходимо из всего многообразия свойств живой нервной клетки выбрать те, которые кажутся наиболее существенными для выполнения поставленной экспериментатором задачи. Этот процесс часто называют формализацией нейрона. Первая модель нейрона, дающая его формальное описание и позволяющая применять аппарат математической логики для анализа и синтеза сетей из нейронов, была предложена У. С. Мак-Каллоком и У. Питтсом. Допущения, введенные ими, сводятся в основном к тому, что нейрон:

1) имеет n входов и один выход (аксон) с одной или несколькими концевыми пластинами;

2) может находиться в одном из двух состояний: возбуждения или покоя (т. е. работает но принципу "все или ничего");

3) входы (синапсы) бывают возбуждающими и тормозящими; активность какого-либо тормозящего синапса абсолютно исключает возбуждение данного нейрона;

4) характеризуется некоторым определенным числом синапсов, при одновременном возбуждении которых он сам приходит в состояние возбуждения, это число не зависит от предыдущего состояния нейрона и от расположения синапсов на нем.

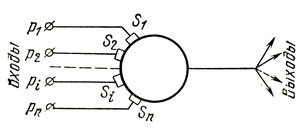
Рис. 93. Модель нейрона

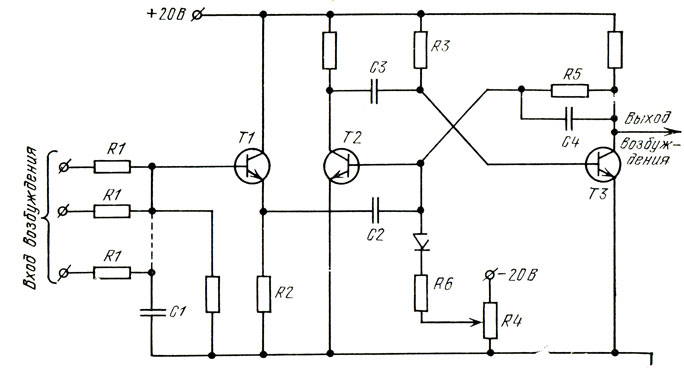
Рис. 94. Модель нейрона Мак-Каллока-Питтса

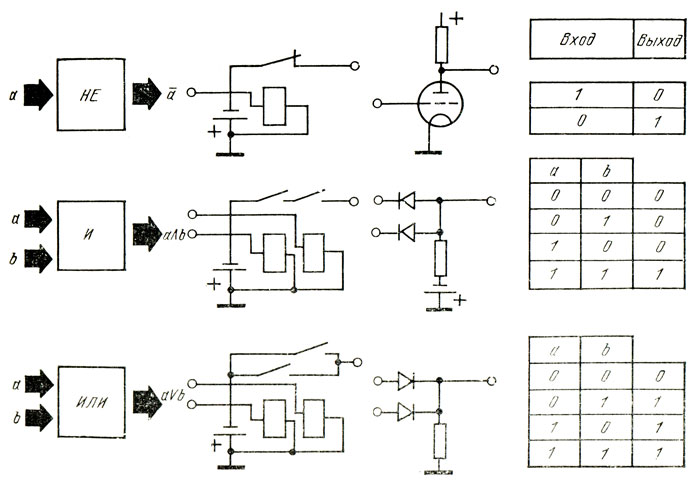
Рис. 95. Логические устройства из реле

Легко видеть, что три последних положения лишь частично отражают реальные свойства нейрона. Дело в том, что эта модель является математической абстракцией, предназначенной для моделирования нейронных сетей на цифровых вычислительных машинах. Электронные модели нейрона гораздо точнее копируют его свойства.

Для имитации нейронов применяются магнитные ферритовые сердечники, схемы специальных генераторов (мультивибраторов) и другие устройства. Модель нейрона Мак-Каллока и Питтса с мультивибратором показана на рис. 94.

Такая схема позволяет воспроизвести многие характеристики нейрона, кроме его способности адаптации, т. е. изменения порога срабатывания в зависимости от величины входных сигналов. Следует иметь в виду, что нейронная схема Мак-Каллока и Питтса является очень упрощенной моделью нейрона. Биологический нейрон значительно сложнее. Один биологический нейрон способен сочетать в себе функции, для реализации которых потребовалась бы целая сеть упрощенных нейронов. Но полная модель была бы необозримой и не поддающейся анализу теми аналоговыми и математическими средствами, которыми мы в настоящее время располагаем.

В действительности сами генераторы нейронных сигналов являются решающими элементами необычайно тонкой структуры, каждый из которых принимает решение о подаче выходного сигнала на основании сложной зависимости от серии сигналов, поступающих на каждый из его синапсов или на рецепторную область, а также в зависимости от его собственного внутреннего состояния.

Для упрощения моделей инженеры интерпретировали информацию, полученную от нейрофизиологов, таким образом: нейрон с его способностью находиться только в двух состояниях (возбуждения и торможения) представляет собой (упрощенно) биологический вариант двухпозиционного реле - электронного или любого другого. Возможности отдельного нейрона, так же как и одного реле, весьма ограничены. Из множества нейронов или реле, работающих на замыкание и размыкание контактов, можно построить логические сети, выдающие на своем выходе, в зависимости от поступающих входных сигналов, различные разумные решения.

Как известно, электромагнитное реле представляет собой небольшую магнитную катушку на железном сердечнике, притягивающемся к сердечнику якоря, и связанных с ним двух или больше пар контактных пластин, которые включаются в электрическую цепь. Если к магнитной катушке прикладывать напряжение, то сердечник намагничивается, притягивает якорь и контактные пластины либо соединяются, либо разъединяются. В результате создается или нарушается электрическая связь, которая была в состоянии покоя реле. Первая электрическая машина Цузаса содержала 2000 электромагнитных управляемых переключателей, а машина Айкена - 3000.

Одного реле достаточно, чтобы построить схему отрицания. Ее входом является обмотка реле, выходом - контактные пластины, одна из которых связана с батареей. Если на входе нулевое напряжение, т. е. на обмотке реле нет напряжения, то обе контактные пластины соединяются, а напряжение батареи подключается к выходу - там появляется 1 (рис. 95).

Если на вход 1 подать напряжение (магнит возбуждается), то контакты прерываются и батарея отключается. На выходе появляется 0. Это свойство схемы отрицания (НЕ).

Для схем И и ИЛИ нужны два реле с рабочими контактами, которые разомкнуты при невозбужденных магнитных катушках. Для реализации схемы И пары контактов обоих реле соединяются последовательно. В этом случае, когда к обеим катушкам реле одновременно приложено напряжение, обе пары контактов будут замкнуты, напряжение батареи подключится на выход и там появится 1.

Если только на одном из входов 0, то и на выходе будет 0. В схеме ИЛИ обе пары контактов включены параллельно. В этом случае достаточно, чтобы напряжение было подано на одно или другое реле, чтобы на выходе схемы появилась 1 (напряжение батареи).