Передаточное отношение зубчатой передачи с паразитами

Одна пара зубчатых колес

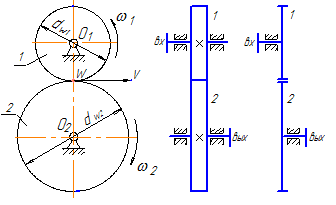
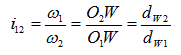
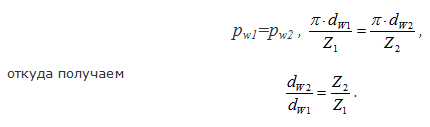
При пересопряжении зубьев следующий зуб второго колеса должен попасть в следующую впадину первого, т.е. шаги на начальных окружностях находящихся в зацеплении колес должны быть одинаковыми:

Таким образом, для одной пары колес передаточное отношение прямо пропорционально отношению угловых скоростей и обратно пропорционально отношению чисел зубьев колес, составляющих пару:

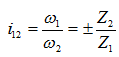
Знак передаточного отношения показывает направление вращения колеса на выходе по отношению к направлению вращения на входе:

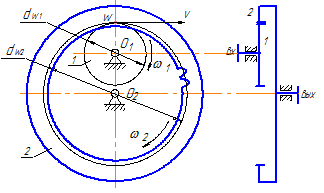
• (+) – направления вращения на входе и на выходе совпадают. Для пары колес направление вращения совпадает при внутреннем зацеплении (рисунок 35б);
• (–) – колеса вращаются в противоположные стороны. Это происходит при внешнем зацеплении (рисунок 35а).

На рисунке 35 дана фронтальная проекция передач, а также их условное изображение на кинематических схемах при виде сбоку (или в разрезе).

Многоступенчатая передача

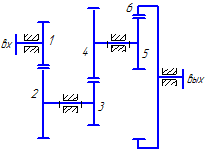
Для увеличения кинематического эффекта несколько зубчатых пар могут последовательно соединяться в единый механизм. Такой механизм называется многоступенчатым зубчатым механизмом или многоступенчатой передачей. Схема одного из таких механизмов приведена на рисунке 36.

Запишем передаточные отношения для каждой пары колес данного механизма:

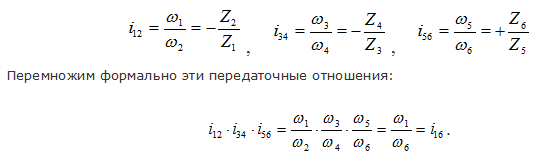
Из схемы видно, что колеса 2 и 3 находятся на одном валу и вращаются с одной угловой скоростью ( ω₂ = ω₃ ), аналогично ω₄ = ω₅ . Поэтому в приведенном выше уравнении эти члены сократились.

Таким образом, общее передаточное отношение многоступенчатого механизма равно произведению частных передаточных отношений ступеней, из которых состоит данный механизм:

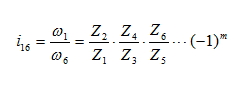
Планетарные и дифференциальные механизмы

В практике применяются зубчатые механизмы, имеющие колеса с подвижными геометрическими осями (сателлиты). Такие механизмы называются планетарными (если имеют одну степень свободы) или дифференциальными (если степень свободы равна двум).

Планетарные и дифференциальные механизмы позволяют получить более высокий кинематический эффект, более высокий кпд, более удобную компоновку. Дифференциальные механизмы позволяют также раскладывать одно движение на два или складывать два движения в одно.

При кинематическом исследовании дифференциальных и планетарных механизмов применяется метод обращения движения (по-другому его называют методом остановки водила). Смысл этого метода заключается в том, что если всем звеньям системы добавить (с любым знаком) одну и ту же скорость, то характер относительного движения этих звеньев не изменится.

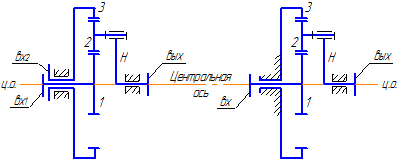
Рассмотрим решение с помощью этого метода на примере механизмов, изображенных на рисунке 37. Пусть звенья этого механизма имеют соответственно угловые скорости: ω₁ , ω₂ , ω₃ , ω_H .

Добавим всем этим звеньям угловую скорость (– ω_H ). Тогда они будут иметь следующие скорости: ( ω₁– ω_H ), ( ω₂ – ω_H ), ( ω₃ – ω_H ), ( ω_H – ω_H ) = 0. Водило стало неподвижным, значит и ось сателлита 2 также стала неподвижной, т.е. механизм превратился в обычный многоступенчатый механизм с неподвижными осями всех зубчатых колес.

Записываем уравнение передаточного отношения между центральными колесами этого многоступенчатого механизма (для того, чтобы отличить передаточное отношение механизма с остановленным водилом от первоначально заданного, в верхнем индексе ставят обозначение водила H. Для данного примера читается – передаточное отношение от первого к третьему при остановленном водиле):

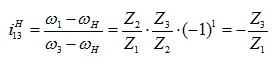
Формулу такого типа, полученную на основе метода обращения движения, называют формулой Виллиса. В данном конкретном механизме (рисунок 38) имеется еще одна особенность – колесо 2 входит последовательно в два зацепления (с первым и третьим колесами), являясь ведомым для первого колеса и ведущим – для второго.

Полученная формула является универсальной для обоих механизмов, изображенных на рисунке 37. Дифференциальный механизм, изображенный на рисунке 37а, имеет две степени свободы, а поэтому для определенности движения надо задать законы движения двум звеньям. При этом возможны следующие варианты:

1. заданы ω₁ и ω₃ ; из записанной формулы определяется ω_H (вариант, изображенный на рисунке 37 а);
2. заданы ω₁ и ω_H ; из записанной формулы определяется ω₃ ;
3. заданы ω_H и ω₃ ; из записанной формулы определяется ω₁ .

Так как звеньям можно задавать любые законы движения, то, как частный случай, одному из центральных колес зададим угловую скорость, равную нулю. Например, в рассматриваемом механизме зададим ω₃=0 , другим словами, затормозим третье колесо. Таким приемом отнимается одна из двух степеней свободы, и механизм из дифференциального превращается в планетарный (рисунок 37 б).

Таким образом, планетарный механизм это частный случай дифференциального, когда одно из центральных колес неподвижно (заторможено).

Поэтому решаются эти механизмы совершенно одинаково, по одним и тем же уравнениям, только в планетарном механизме для неподвижного колеса в уравнение подставляется значение угловой скорости, равное нулю. Для изображенного на рисунке 37б планетарного механизма:

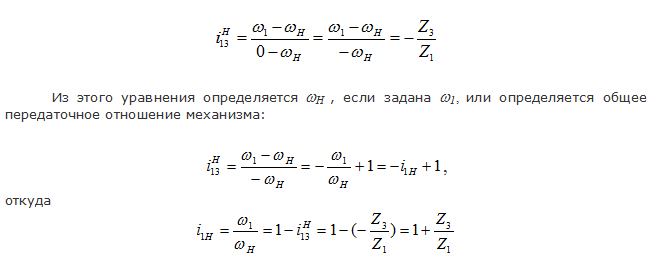
Здесь приведен конкретный пример решения, но на самом деле на этом примере надо усвоить метод решения, подход к решению такого рода задач, т.к. метод один, но для каждой схемы механизма будут получаться свои уравнения.

Сложные механизмы

Существуют механизмы, включающие в свой состав различные части (обычные, планетарные, дифференциальные). В этом случае необходимо разделить механизм на части, записать уравнения передаточных отношений для каждой из них, используя соответствующий метод решения.

Совместным решением полученных алгебраических уравнений находят общее передаточное отношение механизма. (Пример см. в рекомендациях по выполнению расчетно-графического задания).

Рассматривая тему деталей машин, нельзя не уделить внимания такому важному техническому показателю, как передаточное отношение. Этот термин существует уже достаточно давно и о его значении в механике стоит поговорить отдельно.

Формулировка

Передаточное отношение – одна из самых важных технических характеристик любой механической передачи вращательного движения. С практической точки зрения, описываемый показатель позволяет понять, во сколько раз вырастает момент силы в результате функционирования передачи. Определение передаточных отношений в любом механизме – одна из самых главных задач в механике и машиностроении.

Некоторые тонкости

Передаточное отношение определяется при наличии как минимум двух зубчатых колес (шестерен), которые находятся в зацеплении между собой. Такое сопряжение именуется зубчатой передачей.

Самый простой способ рассчитать передаточное число – посчитать количество зубьев на каждом из имеющихся колес, а после произвести деление числа зубьев ведомой шестерни на количество колес ведущей шестерни. Данное рациональное число и будет являться передаточным отношением.

Важно иметь в виду, что в случае определения передаточного числа в зубчатой передаче, имеющей несколько шестерен, необходимо опять-таки делить количество зубьев ведущего колеса на количество ведомого. При этом параметры промежуточных шестерен не учитываются.

Обзор передач

На сегодняшний день существуют такие виды механических передач:

В целом же, механические передачи разделяются по таким критериям:

• В зависимости от передачи движения от ведущего звена к ведомому: передачи трением и передачи зацеплением.
• В зависимости от соотношения скоростей ведомого и ведущего звеньев: замедляющие передачи (они же редукторы), ускоряющие передачи (мультипликаторы).
• В зависимости от расположения осей валов: передачи с перекрещивающимися, пересекающимися и параллельными осями.

Стоит указать, что замедляющие передачи на практике применяются гораздо чаще, нежели ускоряющие. Этот факт объясняется тем, что скорости вращения двигателей зачастую гораздо выше требуемой скорости вала исполнительного механизма или машины.

Зубчатая передача

Передаточное отношение зубчатой передачи можно вычислять не только по соотношению зубьев ее колес, но также путем деления значения угловой скорости ведомого вала на угловую скорость ведущего вала, а также благодаря соотношению числа оборотов ведомого и ведущего валов.

Диапазон передаточного отношения может быть очень велик и достигать больших значений. При этом само по себе передаточное отношение зубчатой передачи характеризуется постоянством, так как зацепление не подвержено проскальзыванию. Коэффициент полезного действия такой передачи находится в пределах 0,97-0,98.

Зубчатые передачи передают вращение между валами, которые могут иметь параллельные, скрещивающиеся или перпендикулярные оси. Кроме того, такие передачи способны трансформировать (преобразовывать) поступательное движение во вращательное и наоборот (передчи "винт-гайка").

Зацепление в зубчатых передачах может быть как внешним, так и внутренним. Колеса изготавливаются с прямыми, косыми или шевронными зубьями.

Зубчатые передачи способны передавать большие скорости вращения с постоянным передаточным отношением и имеют высокий КПД.

Передаточное отношение редуктора является одним из важнейших критериев в процессе его выбора. Вторым по важности показателем считается межосевое расстояние.

Червячная передача

Используется для передачи вращательного движения в тех случаях, когда оси валов перекрещиваются.

Червяк может быть цилиндрическим или глобоидным в зависимости от поверхности расположения резьбы, а также может быть эвольвентным или архимедовым (в данном случае решающую роль играет профиль резьбы).

Основными недостатками описываемой передачи можно считать:

• Высокий показатель тепловыделения.
• Частое заедание и невысокий КПД.

Волновая передача

Ее работа основывается на принципе трансформации параметров движения благодаря волновому деформированию гибкого элемента механизма. По сути, такая передача является разновидностью планетарной передачи.

В состав волновой передачи входит жесткое колесо зубчатое, имеющее внутренние зубья, и вращающееся гибкое колесо с наружными зубьями. Оба колеса между собой входят в зацепление благодаря генератору волн, соединенному непосредственно с корпусом передачи.

За счет имеющихся конструктивных особенностей волновая передача наделена следующими достоинствами:

• Небольшие габариты и масса.
• Высокая кинематическая точность.
• Передаточное отношение передачи в одной ступени имеет большой показатель и вполне может достигать 300.
• Идеальная демпфирующая способность.
• Формирование в одной ступени большого передаточного отношения.

К недостаткам же относятся:

• Весьма сложная конструкция.
• Высокие потери мощности на трение и деформацию гибкого колеса (КПД составляет порядка 0,7-0,85).

Фрикционная передача

Чаще всего применяется в текстильной отрасли, станкостроении и прочих сферах промышленности, кроме авиастроения. Передаваемая мощность может достигать 10 кВт. При больших показателях очень трудно гарантировать требуемое усилие прижатия катков.

В передаче существует три вида скольжения: геометрическое, упругое и буксование.

Для нормально функционирующей передачи характерно именно упругое скольжение, в то время как буксование говорит о наличии перегрузки.

Ременная передача

Как и зубчатая она встречается очень часто. В зависимости от того, как располагаются валы и ремень, передача может быть:

• Открытой.
• Перекрестной.
• Полуперекрестной.
• Угловой.
• Спаренной.
• Ступенчатой.

Ремень может быть круглым, плоским, трапецеидальным.

Передаточное отношение в таких передачах находится в пределах 1:4, 1:5 и лишь в редких случаях может быть равно 1:8.

К положительным качествам ременной передачи следует отнести:

• Простоту конструкции.
• Возможность расположения обоих шкивов на большом расстоянии друг от друга (свыше 15 метров).
• Бесшумность и плавность работы.
• Защиту механизмов от перегрузок благодаря упругим свойствам ремня и его способности в определённые моменты проскальзывать по поверхностям шкивов.
• Работу при больших угловых скоростях.

Недостатками передачи являются:

• Удлинение ремней (их вытягивание) в процессе работы, то есть недолговечность.
• Непостоянство передаточного числа, что объясняется неизбежным проскальзыванием ремня.
• Достаточно большие размеры.

Цепная передача

В отличие от ременного аналога не подвержена проскальзыванию. Расчет передаточного отношения выполняется по аналогии с зубчатой передачей, ведь звездочки передачи, по сути, представляют собой те же зубчатые колеса.

Характерная особенность цепной передачи – вращение передается исключительно при наличии параллельных валов. Между осями звёздочек расстояние необходимо принимать не менее величины полутора диаметров большой звездочки. При этом передаточное число может достигать показателя 1:15.

Также важно заметить, что цепь надевается на звездочки не с натягом, как ремни, а с определенной степенью провисания. Регулировка натяжения проводится с помощью специального винта.

Достоинства передачи таковы:

• Небольшая чувствительность к неточностям установки валов.
• Передача вращения может осуществляться одной цепью сразу же нескольким звездочкам.
• Вращение может передаваться на большие расстояния.

Недостатком же является высокий шум и износ цепей в случае некачественного монтажа и при плохом техническом обслуживании.

Храповый механизм

Во многих машинах и агрегатах применяется не только непрерывное вращательное движение, но и прерывистое тоже, которое осуществляется с помощью храповика, собачки и рычага.

Храповый механизм помимо вращения еще и осуществляет предохранительную функцию. Так, например, в грузоподъемных лебедках, храповик совместно с собачкой не позволяют барабану проворачиваться в обратную сторону, надёжно фиксируя его в требуемом пространственном положении.

Рассмотренные виды механических передач применяются практически в любой отрасли народного хозяйства и получили широчайшее распространение благодаря своим техническим возможностям.

Лабораторная работа №14

Определение передаточных отношений зубчатых передач

Цель работы – изучить различные виды зубчатых передач, научиться определять тип и вид зубчатых передач, их передаточные отношения и передаточные числа.

Зубчатая передача – трехзвенный механизм, в котором два подвижных звена являются зубчатыми колесами, образующими с неподвижным звеном вращательную или поступательную пару (рис.1).

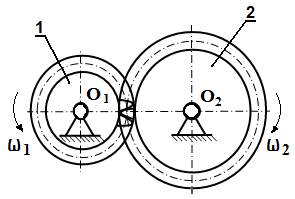
Рис.1. Зубчатая передача с внешним зацеплением

Парное зубчатое колесо - зубчатое колесо передачи, рассматриваемое по отношению к другому зубчатому колесу данной передачи. Зубчатое колесо 2 (рис.1) является парным колесу 1, зубчатое колесо 1 парное колесу 2.

Шестерня – зубчатое колесо передачи с меньшим числом зубьев.

Колесо – зубчатое колесо передачи с большим числом зубьев.

Передаточное отношение зубчатой передачи – это отношение угловой скорости ведущего зубчатого колеса к угловой скорости ведомого зубчатого колеса .

Ведущее зубчатое колесо – зубчатое колесо передачи, которое сообщает движение парному зубчатому колесу.

Ведомое зубчатое колесо - зубчатое колесо передачи, которому сообщает движение парное зубчатое колесо.

Рис.2. Виды зубчатых зацеплений: внешнее (слева) и внутреннеее

Передаточное число зубчатой передачи – это отношение числа зубьев ведомого зубчатого колеса к числу зубьев ведущего колеса. Передаточное число зубчатой передачи определяется по формуле:

Типы зубчатых передач

Цилиндрическая зубчатая передача (показана на рис.3, ее кинематическая схема – на рис.1) - зубчатая передача с параллельными осями, у зубчатых колес которой аксоидные, начальные и и делительные поверхности цилиндрические. В этих передачах относительное расположение осей вращения колес определяется только межосевым расстоянием.

Аксоидная поверхность зубчатого колеса – каждая из поверхностей, описываемых мгновенной осью относительного движения зубчатых колес передачи, относящаяся к данному зубчатому колесу. В цилиндрической и конической передачах начальные поверхности совпадают с аксоидными.

Коническая зубчатая передач (показана на рис.3) - зубчатая передача с пересекающимися осями, у зубчатых колес которой аксоидные, начальные и и делительные поверхности конические. В этих передачах относительное расположение осей вращения колес определяется только углом между осями.

Ортогональная зубчатая передача (показан на рис.3) – коническая зубчатая передача, угол между осями которой равен 90°.

Неортогональная зубчатая передача – коническая зубчатая передача, угол между осями которой отличен от 90°.

Рис.3. Типы зубчатых передач (слева), коническая (в центре), винтовая зубчатая передача

Зубчатая передачи со скрещивающимися осями вращения колес (рис.3) - зубчатая передача, в которой относительное расположение осей вращения колес определяется межосевым расстоянием и углом между осями. Существует много вариантов таких механизмов. На рис.3 показана винтовая зубчатая передача, угол между осями которой составляет 90 °. Другой вариант передачи с углом между осями в 90 ° - червячная передача (рис.4). Шестерня червячной передачи называется червяком (поз.1 на рис.4) , а колесо – червячным колесом (поз.2 на рис.4) . Вторая передача, показанная на рис.4, называется гиперболоидной. Аксоиды ее зубчатых колес – однополостные гипеболоиды вращения.

Для конических зубчатых передач и передач со скрещивающимися осями передаточное отношение определяется по тем же формулам, что и для цилиндрических передач, но без учета знаков.

Рис.4. Червячная (слева) и гиперболоидная зубчатая передача

Виды зубчатых колес

Рис.5. Виды зубчатых колес: цилиндрическое косозубое (слева), шевронное (в центре),

В зависимости от вида зубьев зубчатые колеса цилиндрических передач делятся на прямозубые (рис.3 слева), косозубые и шевронные (рис.5). Зубчатые колеса конических передач – на прямозубые (рис.5), тангенциальные, с круговым зубом (рис.3 в центре), с криволинейным зубом.

В зависимости от профиля зубьев зубчатые колеса и передачи делятся на эвольвентные (рис.2, рис.6), циклоидальные, зубчатые колеса цилиндрической передачи Новикова (рис.6), профили зубьев которой контактируют по дуге окружности.

Рис.6. Виды зубчатых колес: с эвольвентным профилем зубьев (слева),

зубчатые колеса передачи Новикова

МНОГОСТУПЕНЧАТЫЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ

Зубчатые передачи с неподвижными осями вращения колес

Рис.7. Двухступенчатая зубчатая передача и ее кинематическая схема

Простейший зубчатый механизм (рис.1) состоит из двух зубчатых колес ведущего и ведомого, которые одновременно являются входным и выходным, соответственно. Для получения необходимых передаточных отношений в машинах и приборах часто применяют сложные зубчатые механизмы, имеющие кроме входного и выходного колес несколько промежуточных колес, каждое из которых вращается вокруг своих осей. Применение сложных механизмов объясняется различными причинами. Например, оси входного и выходного колес расположены далеко друг от друга. В этом случае непосредственная передача вращения при помощи двух колес потребовала бы создания передачи с большими габаритами. В другом случае передаточное отношение может быть очень велико или очень мало, тогда удобно между входным и выходным колесами иметь промежуточные колеса со своими осями. Передавая вращение с входного колеса на промежуточные колеса и с них на выходное колесо, мы как бы последовательно отдельными ступенями изменяем скорость вращения звеньев, получая в результате требуемые передаточные отношения между входным и выходным колесами.

Таким образом, сложный механизм передачи можно разделить на отдельные части – ступени, каждая из которых представляет собой два колеса, образующих зубчатое зацепление. В соответствии с указанным бывают одно- и многоступенчатые передачи, по большей части двух- и трехступенчатые (рис.7). Количество ступеней равно числу зубчатых зацеплений, образованных зубчатыми колесами механизма. Одно колесо может входить в несколько ступеней (рис.8). Любая ступень может представлять собой цилиндрическую, коническую, червячную, глобоидную и т.д. передачу. На рис.8 показан многоступенчатый механизм, содержащий цилиндрические и конические ступени.

Рис.8. Многоступенчатая зубчатая передача

с паразитными колесами

Общее передаточное число (отношение) зубчатой передачи при последовательном соединении ступеней равно произведению передаточных чисел входящих в них ступеней. Для передачи на рис.7:

Зубчатые колеса, числа зубьев которых не влияют на общее передаточное отношение механизма, называются паразитными колесами . Для четырехступенчатой передачи, показанной на рис.8, передаточное число равно:

Планетарные зубчатые передачи

В некоторых многоступенчатых зубчатых передачах оси отдельных колес являются подвижными. Такие зубчатые механизмы с одной степенью свободы называются планетарными механизмами (рис.9) , а с двумя и более степенями свободы – дифференциальными механизмами или просто дифференциалами. В этих механизмах колеса с подвижными осями вращения называются сателлитами (звено 2 на рис.9) , а звено, в котором установлены сателлиты - водилом. На схемах водило принято обозначать буквой Н. Зубчатые колеса, оси которых совпадают с осью вращения водила, назыаются центральными (звенья 1 и 4 на рис.9). Сателлиты бывают одновенцовые (левый рисунок) и многовенцовые.

Передаточное число планетарного механизма определяется по формуле:

На рис.10 приведены формулы для определения передаточных чисел планетарных механизмов. Передаточные числа между подвижным центральным колесом и водилом связаны соотношением:

Рис.10. Определение передаточных чисел планетарных механизмов

При выборе чисел зубьев колес планетарных зубчатых передач для них проверяются условия:

2. Условие соседства, обеспечивающее совместное размещение нескольких сателлитов по общей окружности в одной плоскости, без соприкосновения вершин зубьев соседних сателлитов:

Условие соседства получено для планетарных передач, у которых сателлиты располагаются равномерно по окружности водила.

3. Условие сборки зубчатых колес передачи, определяющее возможность сборки передачи при использовании нескольких сателлитов:

где П- число полных поворотов водила 0,1,2,3. Ц- целое число 1,2,3, .

Макеты цилиндрических, конических, червячных, многоступенчатых и планетарных зубчатых механизмов.

Порядок выполнения работы

1. Получить задание и лабораторные макеты у преподавателя.

Каждый студент должен определить передаточное отношение и передаточное число пяти зубчатых передач:

1) цилиндрической зубчатой передачи;

2) конической зубчатой передачи;

3) зубчатой передачи со скрещивающимися осями;

4) многоступенчатой передачи с неподвижными осями колес;

5) планетарной зубчатой передачи.

2. Для каждой передачи:

2.1. Нарисовать кинематическую схему.

2.2. Дать полное название зубчатой передачи (определить ее тип и вид). Например, механизм, показанный на рис.7, называется цилиндрическая косозубая эвольвентная зубчатая передача.

2.3. Определить подвижность передачи по формуле Малышева для плоских механизмов.

2.4. Опытным путем определить передаточное отношение зубчатой передачи. Для этого посчитать число оборотов ведущего колеса соответствующее целому числу оборотов ведомого колеса.

2.5. Рассчитать передаточное число аналитически. Для чего посчитать числа зубьев колес передачи и по формулам найти передаточное число.

Для сложных зубчатых передач определить количество ступеней, указать паразитные колеса. Рассчитать передаточное число механизма, выразив его через числа зубьев колес.

2.6. Для планетарной передачи проверить выполнения условий соосности, соседства и сборки.

2.7. Составить сложную зубчатую передачу, соединив последовательно три из рассмотренных зубчатых передач. Нарисовать ее кинематическую схему и опредилить общее передаточное отношение.

2.8. Все результаты занести в отчет по лабораторной работе.

1. Перечислить звенья, входящие в простейшие зубчатые механизмы.

2. Перечислить звенья, входящие в сложные зубчатые механизмы.

3. Цель использования многоступенчатых передач.

4. Перечислить основные типы зубчатых передач.

5. Написать формулу для определения передаточного числа многоступенчатой зубчатой передачи.

6. Написать формулу для определения передаточного числа одноступенчатой зубчатой передачи.

7. В чем достоинства и недостатки прямозубых и косозубых зубчатых колес?

8. Чем планетарная зубчатая передача отличается от непланетарной ?

9. Зачем устанавливают несколько сателлитов в планетарном механизме?

10. Как определить передаточное число планетарной зубчатой передачи?

11. Какие условия проверяются для планетарной передачи? В чем их смысл?

12. Когда учитываются знаки передаточных чисел ступеней зубчатой передачи?

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Одной из важнейших кинематических характеристик в теории механизмов и машин является передаточное отношение. Оно позволяет определить, на какую величину возрастает момент приложенной силы, когда происходит передача вращения от одной детали к другой. На практике для решения различных технических задач механизмы создаются с кинематической схемой, имеющей постоянное или переменное передаточное отношение.

Общее определение

Значение передаточного отношения у кинематических схем рассчитывается по стандартному математическому выражению. Результат получается при проведении математической операции деления значения угловой скорости ведущего вала или шестерёнки, на такой же параметр ведомого вала. Вместо этих значений используют отношение их частот вращения.

Современные кинематические схемы реализованы с использованием следующих механических соединений:

• с зубчатым зацеплением (в разных вариациях);
• червячных;
• фрикционных соединений;
• с помощью цепей;
• посредством специальных ремней;
• планетарных соединений.

Передача вращения основана на двух физических принципах: с помощью силы трения, с использованием механизмов зацепления. В зависимости от решаемой задачи механизмы изготавливаются с замедлением и ускорением. Первые называются редукторами, вторые — мультипликаторами. Обе разновидности бывают одноступенчатыми, двухступенчатыми, многоступенчатыми.

Пространственное расположение осей определяет следующие виды механизмов:

• параллельные (в них оба вала расположены параллельно друг относительно друга);
• пересекающиеся (зацепление происходит посредством пересечения);
• перекрещивающиеся механизмы (у них валы вступают в перекрестное зацепление).

Все типы механизмов бывают замедляющие и ускоряющие движение. Наиболее частое применение замедляющих конструкций объясняется более высокой скоростью используемых двигателей и необходимостью увеличить мощность выходного элемента кинематической схемы.

В зависимости от соотношения скоростей возникает вопрос: может ли передаточное отношение быть отрицательным? Этот коэффициент является отношением величин имеющих только положительные значения. Он не может быть отрицательным. В зависимости от отношения числителя к знаменателю результат получиться больше единицы или меньше. В первом случает, он справедлив для редукторов, во втором для мультипликаторов.

Таблица передаточных отношений является сводным документом. В ней приведены значения основных технических характеристик всех типов кинематических соединений.

В сводной таблице можно найти зависимость значения передаточного числа от допустимой мощности, которая передаётся конкретным видом соединения.

Зубчатая передача

Это механическое соединение двух или более вращающихся валов при помощи специальных колёс, на поверхности которых выточены зубья. Такой тип подразделяется по следующим характеристикам:

• форме и типу зубьев;
• относительному расположению валов в корпусе;
• расчётной скорости вращения колёс;
• степени защиты от внешних воздействий.

Важную роль в понимании работы всего механизма играет передаточное отношение зубчатой передачи. Его вычисляют, используя классическое выражение. Оно находится с подстановкой различных параметров. Например, подсчитывая численность изготовленных зубьев на ведущем и ведомом колесе. Формула позволяет получать результаты с высокой степенью точности:

Где i₁₂ — передаточное отношение от звена 1 к звену 2 (звено 1 — ведущее, звено 2 — ведомое; d₁,d₂ — диаметры звеньев; z₁, z₂ — количество зубьев звеньев (если таковые имеются); M1, M2 — крутящие моменты звеньев; ω₁, ω₂ — угловые скорости звеньев; n₁, n₂ — частоты вращения звеньев.

В большей степени он зависит от количества зубьев расположенных на шестерёнке. Существенным достоинством зубчатого соединения является постоянство расчётного и реального передаточного отношения. Она связано с отсутствием эффекта проскальзывания.

Существенное влияние на величину этого показателя оказывает применяемое количество шестерней и число зубчатых колёс.

Для цилиндрической передачи этот параметр кроме приведенных выше параметров зависит от межосевого расстояния. Цилиндрические зубчатые передачи распространены в различных агрегатах легковых и грузовых автомобилей, тракторов, сельскохозяйственной техники. Их активно используют в трансмиссии.

Зубчатая передача обладает самым большим коэффициентом передачи мощности. Она способна отдавать мощность до 4500 кВт с передаточным числом достигающим 6,3.

Распространение получили зубчатые конструкции конического типа. Они обладают ортогональным сочленением. Расчёт конической передачи предполагает учёт таких параметров как: делительные диаметры, углы конусов, количество зубьев.

Для получения поступательного движения применяется реечное соединение. Конструктивно она состоит из шестерёнки, рейки с нанесёнными зубьями. Для реечной передачи учитывают диаметр окружности и количество зубьев на колесе, число зубьев расположенных на рейке.

Планетарная передача

Широко применяется так называемая планетарная кинематическая схема. Она представляет собой механизм, предназначенный для передачи, преобразования вращательного движения. С этой целью используются зубчатые колеса, расположенные на перемещающейся оси. Конструктивными элементами являются: центральные зубчатые колеса, закреплённые на неподвижных осях, боковые зубчатые колеса (расположены на перемещающихся осях). Для обеспечения наилучшего эффекта планетарные механизмы изготовляются на параллельных осях.

Максимальное значение передаточного числа достигает 9 единиц.

Коэффициент полезного действия достаточно высокий. Его значение приближается к 0,98. Наиболее распространёнными являются конструкции, в которых применяются нескольких сателлитов. Их располагают с угловыми шагами равной величины.

Такие конструкции выполняются с постоянным или переменным передаточным отношением. Некоторые из них имеют возможность регулировки этого параметра. Они разработаны обратимыми и необратимыми. В обратимых образцах предусмотрено движение в прямом и обратном направлении. В необратимых конструкциях такое движение невозможно. Изменение передаточного отношения бывает ступенчатым или бесступенчатым. Ярким представителем первого агрегата является механическая коробка передач автомобиля. Второй вариант применяется в вариаторах.

Рассмотренные передаточные отношения передач рассчитываются на этапе проектирования агрегата при выборе кинематической схемы. С их помощью производится выбор типа соединения, определяется эффективность. Оценивается надёжность всего механизма.

Цепная передача

Хорошо известна цепная передача. Она относится к гибким конструкциям. Передаточное отношение цепной передачи рассчитывается расчёту зубчатых систем. Ведущая и ведомая звёздочка рассматриваются как зубчатые колеса. Значение этого параметра достигает 15.

Особенностью такой конструкции считается требование иметь определённое провисание цепи. Настройка этого параметра проводится с помощью специального регулирующего винта.

Достоинства подобного соединения сводятся к следующему:

• низкая критичность к возможным ошибкам при установке валов.
• передача мощности производится с использованием нескольких звездочек;
• длина передачи вращения может быть достаточно большой.

К недостаткам можно отнести быстрый износ соединительных элементов цепи. Это требует периодической смазки. Вторым недостатком считается высокий уровень шума.

Кроме передаточного числа для них рассчитывается величина статистической разрушающей силы. Этот параметр зависит от требуемого коэффициента безопасности. Его задают в интервале от 6 до 10. Он обеспечивает качественную работу всего механизма, высокую надёжность соединения и долговечность.

Червячная передача

Необходимость изменения вращательного движения под углом требует создания специального вида систем. К таким конструкциям относится червячная передача. Основной элемент такой передачи может быть цилиндрической формы, глобоидным, эвольвентным, архимедовым винтом. Это зависит от поверхности, на которой расположена резьба, и профиля резьбы.

В качестве параметров, используемых для расчёта передаточного числа подставляемых в выражение, используют существующее количество заходов червячного механизма. Обычно оно варьируется от одного до четырёх. Таблица передаточных отношений для червячной схемы позволяет рассчитать необходимое количество элементов зацепления. Приведенные в этой таблице данные, помогают правильно выбрать соединения для конкретного механизма.

Основными недостатками передачи являются:

• высокая температура нагрева элементов во время передачи вращения;
• наличие эффекта проскальзывания;
• затормаживание и заедание;
• низкий КПД;
• как следствие невысокую надёжность.

Ременная передача

Данная конструкция является часто встречающейся. Её тип определяется расположением вала и направлением движения ремня. Их классифицируют следующим образом:

• открытого типа;
• перекрестной формы;
• ступенчатой системы;
• угловой.

Для повышения надёжности применяют спаренное соединение. Реализация подобных конструкций производится с помощью ремней различного сечения. Наиболее популярными являются три типа: прямоугольные, в форме трапеции, круглого сечения.

Значение передаточного отношения рассчитывается подстановкой в классическую формулу скоростей вращения ведущего и ведомого валов. Иногда в расчёте используют число оборотов каждого из валов. В качестве альтернативного варианта при расчёте этого параметра используются величины диаметров (радиусов) шкивов.