Системы счисления математика 2 класс горбов
Технологическая карта урока математики
Тема урока: Название мерок (разрядов) в десятичной системе счисления.
Тип урока: урок решения частных задач
Цель урока: формировать навык чтения и записи состава многозначного числа в десятичной системе счисления, используя названия мерок (разрядов)
моделировать отношения между мерками (разрядами) в десятичной системе счисления
уточнить названия мерок (разрядов) в десятичной системе счисления
использовать названия мерок при чтении результата измерения величины
закреплять вычислительные навыки
развивать внимание, память логическое мышление
формировать умение слушать, принимать точку зрения, отличающуюся от собственной, отстаивать свою точку зрения.
Предметные результаты:
называют состав многозначного числа в десятичной системе счисления, используя названия мерок (разрядов)
записывают числа в десятичной системе счисления используя табличную запись.
Формируемые УУД:
-формировать умения самостоятельно выделять и формулировать познавательную цель всего урока и отдельного задания;
-строить логическое рассуждение.
-формировать умение работать в группе, находить общее решение, умение аргументировать своё предложение;
-развивать способность сохранять доброжелательное отношение друг к другу, взаимоконтроль и взаимопомощь по ходу выполнения задания;
-проявлять познавательную инициативу в учебном сотрудничестве.
-формировать способности к самооценке на основе критериев успешности учебной деятельности.
Дидактический материал к уроку : учебник (В.В Давыдов,. С.Ф.Горбов 2 класс), тетрадь, раздаточный материал
Такой способ измерения и построения величин создает особую форму представления числа как результата измерения: оно выражается не отдельным знаком, а целым набором цифр. Это так называемое многозначное число.
Вначале многозначное число представляется в табличном виде, а затем осваивается переход к позиционному способу записи, где смысл каждого знака (цифры) определяется его местом в записи.
Десятичная система счисления рассматривается как частный случай системы построения многозначного числа, которая в силу своей общепринятости получила определенные названия мерок (разрядов).
1. Организационный момент
Эмоциональный настрой учащихся на продуктивную работу
Запись числа, классная работа.
Приветствуют учителя, проверяют готовность к уроку.
Личностные УУД (мотивация)
2. Актуализация необходимых знаний
Использование известного, ранее открытого способа действия
Какую большую тему мы изучаем? Что мы уже умеем? Начертите в своих тетрадях - достижения линейку оценивания. Оцените себя, насколько вы это умеете делать.
Перед вами величина, которую нужно измерить. О какой величине идет речь?
(измерить величину в троичной, четверичной, пятеричной системах счисления), записать результат и прочитать.
Какие вопросы у вас есть к ребятам у доски?
Я измеряла эту величину в шестеричной системе. Правильно ли? 16 (6)
А можете посчитать в (10) системе счисления?
Оцените свою работу, какой критерий выберете?
Измерять и строить величину, записывать в различных системах счисления.
Учащиеся работают на карточке
3 учащихся у доски.
Учащиеся отмечают ошибку, что при записи числа использовали цифру 6. Оценка правильности работы по визуальному образцу.
фомирование познавательной цели;
3. Постановка цели урока
Составление плана урока
О чём узнали на прошлом уроке? Какие цели вы поставили себе на прошлом уроке? Назовите тему сегодняшнего урока. Что для этого будем делать.Как будем их решать.
Тема Название мерок в десятичной системе счисления.
Цель научиться называть и записывать числа в десятичной системе счисления
инициативное сотрудничество в поиске и выборе информации
4. Создание учебной ситуации
Конкретизация общего способа действия
Мы говорили с вами, что исторически сложилось, что общепринятой стала десятичная система счисления.
Каким образом образуются мерки в десятичной системе?
(говорит название разрядов)
Каждая следующая мерка состоит из десяти предыдущих.
Дети строят в группах систему мерок.
В группах вам необходимо измерить величину, изображенную на листах, в десятичной системе счисления и записать результат в таблицу в таблицу.
Какую величину вы будете измерять?
У вас есть система мерок.
Выступление от групп.
1 тысяча, 1 сотня, 2 десятка, 5 единиц
5. Первичное закрепление.
Использование названия мерок при чтении результата измерения величины
Работа по учебнику стр. 83 № 281- используя раздаточный материал покажите на столе 3ед., 4 дес., 2 сот., 2 тыс.
№ 283 – в парах, запишите результат счёта в таблицу.
Самостоятельная работа в Р.Т. стр 54 № 174
Перепешите числа из таблицы в строку и из строки в таблицу.
Пара работает у доски.
*Составь задачу по схеме.
Ловушка, у нас не хватает второй мерки тысяча
Совершенствование навыков оценочной деятельности
Что предстоит на следующем уроке? Какой следующий шаг?
Как удобнее прочитать результат измерения величины в десятичной системе счисления?
Оцените в тетрадках на линеечках свою работу на уроке.
Оценочная деятельность учащихся.
умение с достаточной полнотой и точностью выражать свои мысли;
О чем узнали на уроке, над чем работали?
Домашнее задание на карточках по цвету:
Жёлтая – очень сложная, белая – легче. Есть выбор.
Урок по отработке навыков работы в различных системах счисления
Конспект урока математики, 2Г класс
Учитель Соснина М.В.
Тема: Счет с помощью дополнительных мерок
Цель: научить использовать новый способ измерения и построения величин при помощи набора мерок и системы мерок.
рассмотреть новый способ измерения и построения величин, требующий использования системы дополнительных мерок;
развивать интеллектуальные и коммуникативные умения и навыки, в том числе умения самостоятельно оценивать результат.
Организационный момент.
Учитель: Здравствуйте, ребята!
Проверка Д/З, актуализация ранее полученных знаний.
Целеполагание, мотивирование на получений новых знаний:
- Сегодня на уроке мы попадём в сказочный город. Я расскажу вам одну историю:
"В одной сказке жили гномы-портные. Они очень любили шить. И вот один раз гномы всем жителям сказочного города сшили кафтаны в подарок. Они захотели украсить их красивыми пуговицами и петлями. Все петли должны быть одинаковой длины. Вот такой -
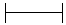
(демонстрируется образец петли - кусок шнура или бумаги длиной 5 см.)
Сейчас вам нужно помочь гномам-портным отмерить от данного клубка такую длину, чтобы ее хватило на петли для одного платья.
На доске имеется отрезок А (длина 95 см). Это как раз та длина, которая нужна. Как нам отмерить ее от клубка? Учтите, что прикладывать тесьму к доске нельзя. Как нам поступить?
Дети: Надо измерить отрезок на доске меркой-петлей, а потом на тесьме отложить столько же мерок, сколько получится.
Цель урока: (формулируют дети) найти новый способ измерения и построения величин с использованием дополнительных мерок
Усвоение новых знаний.
Учитель: Измеряем с одним условием - оказывается, что эти гномы умеют считать только до пяти. Как же они будут действовать в такой ситуации?
Дети: Они досчитают до пяти, а потом начнут сначала: 1,2,3,4,5,;1,2,3,4,5,: и т.д.
К доске выходят два ученика. Один прикладывает мерку, другой считает.
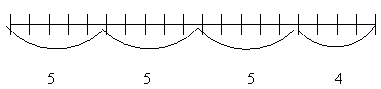
Учитель: Теперь надо отмерить кусок тесьмы. Что надо передать тем, кто будет отмеривать?
Дети: Мерку и число.
Учитель: Какое же из полученных чисел надо передавать?
Дети: Все четыре: 5, 5, 5, 4.
Учитель: Что мы делаем, когда повторяем мерку Е одинаковое количество раз?
Дети: У нас получается новая мерка, допустим К, только увеличенная.
Учитель: Тогда, как вы думаете, сколькими мерками мы пользовались, когда измеряли величину А?
Дети: Двумя разными мерками К и Е.
Учитель: Таим образом, можно сказать, что мы величину А измерили по частям?
У: Покажите это в схеме.
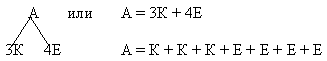
Учитель: А можно ли это записать в таблицу?
Дети: Да, можно.
Учитель: Что же мы передадим отмеривателям?
Дети: Мерку Е и таблицу.
Учитель: Смогут ли они отмерить нужную длину?
Дети: Нет, нужна еще мерка К.
Учитель: А ведь у нас ее нет.
Дети: Ее можно сделать из мерки Е.
Дети: Повторить мерку Е пять раз.
Учитель: Так вот, ребята, эта новая мерка К называется дополнительная, потому что она получена из мерки Е. А мерка Е называется основной. А раз эти мерки взаимосвязаны между собой, то и обозначать мы их будем одной буквой Е. Только для различения еще отмечать цифрой - Е1, Е2. Давайте, поправим таблицу с учетом того, что я сказала.
Учитель: Что-то еще в таблице надо указать?
Дети: То, что мерка Е2 состоит из 5 мерок Е1.
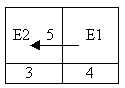
После этого отмериватели получают клубок, мерку и таблицу и отмеривают нужную длину. Затем выполняется проверка. Шнур прикладывают к доске. Отрезок и тесьма равны.
Закрепление новых знаний (первичное).
Учитель: Но к петлям нужны еще и пуговицы. Требуется отсчитать необходимое количество пуговиц равное количеству петель.(19 штук)
На доске изображено в беспорядке 19 точек. Пересчитайте точки и сделайте таблицу, по которой можно было бы отсчитать нужное количество пуговиц из тех, что имеются у меня на столе. (На столе у учителя лежит избыточное количество пуговиц). Но помните, что считать можно только до 5.
Дети группируют точки по 5.
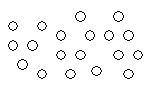
Учитель: То, что получилось, запишите в таблицу.
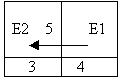
Дети: таблица получилась такая же, как и раньше.
Учитель: А теперь отсчитайте нужное количество пуговиц.
Учебник: стр.33 №113, 114.
Что нового узнали на уроке? Достигли ли поставленной цели?
Когда в древности люди только изобретали счёт, они, как сейчас маленькие дети, считали на пальцах. Пальцев на руках – десять, поэтому и система счисления у нас – десятичная. Однако наша система счёта компьютеру не слишком-то понятна: ему ближе двоичная. У компьютера нет десяти пальцев, но, с другой стороны, и двух тоже нет. Откуда тогда взялась двоичная система, что это за ноль и единица, которыми думает компьютер? И как из них получаются обычные, понятные цифры?

Для того чтобы в общих чертах понять, как думает компьютер, начнём с самого начала. Компьютер, по сути, – это много всякой электроники, собранной вместе в правильном порядке. А электроника (до того, как к ней добавили программу) понимает только одно: включена она или выключена, есть сигнал или нет сигнала.
Этот язык нулей и единиц называют ещё двоичной системой счисления – потому что в ней всего две цифры. Наша привычная система счисления – десятичная, в ней десять цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Но есть и множество других – восьмеричная, пятеричная, одиннадцатиричная и какая угодно ещё.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F, 20, 21, 22…97, 98, 99, 9A, 9B, 9C, 9D, 9E, 9F, A0, A1, A2… F7, F8, F9, FA, FB, FC, FD, FE, FF, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 10A, 10B, 10C и так далее.
Двоичная система счисления, впрочем, тоже выглядит странновато для непривычного взгляда:
0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111, 10000, 10001…
Вот примерно такими числами и думает компьютер где-то внутри себя. Но человеку такими числами думать совершенно неудобно, поэтому мы преобразуем числа из двоичной в более удобную систему счисления.
В компьютерных программах часто используют восьмеричную и шестнадцатиричную системы: компьютеру легко их понять (потому что 8=2*2*2, 16=2*2*2*2, а с двоичной системой компьютер знаком изначально), а для людей это удобно, потому что поближе к привычной десятичной.

Как же переводить числа из одной системы счисления в другую? Чтобы понять принцип, будем, как мы с вами любим, разбираться на конфетах.
И на конфетах мы с вами будем переводить число 33 в восьмеричную систему счисления. Мы решим, что единицы – это сами конфеты, а десятки – это коробки, в каждой из которых лежит по десять конфет. Вот и получится, что 33 – это 3 коробки по 10 конфет и ещё 3 конфеты где-то сбоку.
Но мы переводим наше конфетное богатство в восьмеричную систему счисления, а это значит, что нам надо вытряхнуть все конфеты из коробочек по 10, сложить в коробочки по 8 и посмотреть, что из этого выйдет.
Из 33 получится 4 полных восьмеричных коробочки и 1 конфета останется сама по себе, так как 33/8=4 (ост. 1). То есть 33=8*4+1 – так в восьмеричной системе счисления получается число 41.
33 в десятичной – это 41 в восьмеричной. Это одно и то же число, просто разложенное по разным коробочкам, переведённое в разное основание. Количество конфет не поменялось, мы просто считали их по-разному!
Двоичная система, как мы уже выяснили, более странная и непривычная для человеческого взгляда. Давайте попробуем перевести 33 в двоичную – получится аж 16 коробочек по 2! И что же делать? Писать 16 как-то странно, помня о том, что в двоичной системе есть только ноль и единица, а шестёрки, которая нам нужна для шестнадцати, совершенно точно нет!
Посмотрим на нашу десятичную систему. В ней мы считаем десятки – 10, 20, 30, 40, 50, 60, 70, 80, 90 – а когда у нас набирается десять десятков, мы достаём большую коробку – 100.
У нас 100 – это 10*10, 1000 – 10*10*10, 10 000 – 10*10*10*10 и так далее. Для других систем счисления это работает точно так же! В восьмеричной системе 100=8*8, 1000=8*8*8; в двоичной 100=2*2, а 1000=2*2*2; а в шестнадцатиричной (есть и такая, помните?) 100=16*16, 1000=16*16*16.
Здесь нам пригодятся степени. Если вы их ещё не проходили в школе, не пугайтесь, степени – это очень просто. Число в степени – это число, сколько-то раз умноженное на само себя. То есть 5 3 =5*5*5 (пять в третьей степени – это пять, три раза умноженная сама на себя: 5*5*5), или 8 5 =8*8*8*8*8 (восемь в пятой степени – это восемь, пять раз умноженная на саму себя: 8*8*8*8*8).
Если мы вспомним про наши 10 000=10*10*10*10 в десятичной и 1000=8*8*8 в восьмеричной, то можно легко заметить, что сколько нулей, столько раз и умножаем на само себя. Другими словами, количество символов в числе минус один – это степень, в которую надо возвести основание. В числе 1000 у нас четыре символа, значит умножать надо 4–1, то есть 3 раза. Если основание 10, то тысяча – это 10, три раза умноженная сама на себя: 10*10*10. Если основание 8, то тысяча – это 8, три раза умноженная сама на себя: 8*8*8.
Обо всём этом мы заговорили, пытаясь перевести 33 в двоичную систему. Просто так поделить это число на коробочки по 2 оказалось затруднительным. Но если вспомнить про наши сотни-тысячи, можно задуматься: а ведь в двоичной 100=2*2, 1000=2*2*2, 10 000=2*2*2*2 и так далее.
Для перевода из десятичной системы в двоичную удобно помнить степени двойки. Даже можно сказать, что без этой хитрости со степенями мы устанем, умаемся и немножко сойдем с ума. А степени двойки выглядят как-то так:
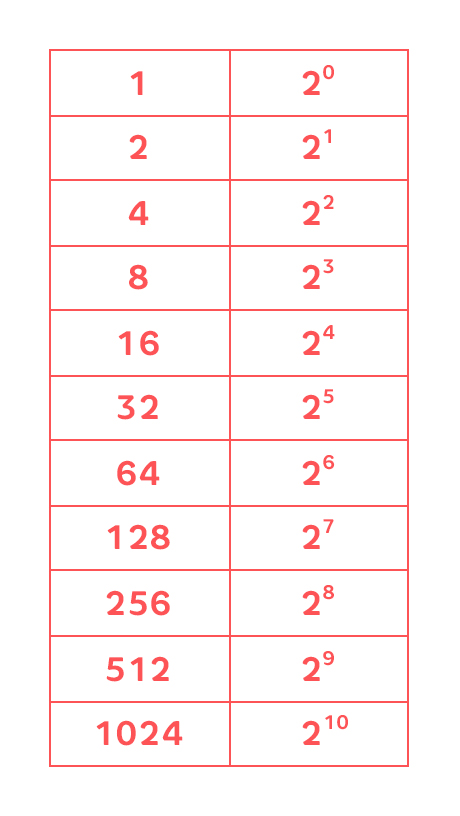
Теперь, глядя на табличку, мы видим, что 33=2 5 +1, то есть 33=2*2*2*2*2+1. Вспоминаем – сколько раз умножаем, столько будет нулей – то есть наше 2*2*2*2*2 в двоичной системе будет 100000. Не забудем оставшуюся в стороне единичку, и получится, что 33 в десятичной – это 100001 в двоичной. Правильно и красиво это записывают так:
Давайте (чтобы совсем хорошо понять) переведём в двоичную систему число 15.
- В первую очередь – смотрим в табличку.
а) Какое самое близкое к 15 число в ней? Нет, 16 не подходит, оно больше, а нам нужно самое близкое, которое меньше. Получается, что это 8, то есть 2 3 , то есть 2*2*2.
б) Восемь конфет из 15 разобрали, осталось – 15-8 – семь. Какое ближайшее число из таблички? Нет, восемь снова не подойдет, см. выше. Подойдет четыре, то есть 2 2 , то есть 2*2.
в) Четыре из семи конфет разобрали, осталось – 7-4 – три. Из таблички понимаем, что самое близкое число – 2, то есть 2 1 , то есть просто 2.
г) Три минус два – осталась 1 конфета, тут уже табличка не понадобится. В таблички такого рода можно не смотреть, когда ваш остаток меньше основания, а наша единица точно меньше двойки.
- Собираем всё найденное в табличке вместе: 15=2 3 + 2 2 + 2 1 + 1, оно же: 15=2*2*2 + 2*2 + 2 + 1.
- В двоичной системе 2*2*2=1000, 2*2=100, 2=10, помните? И у нас получается 1000+100+10+1, то есть 1111.
- Итак,
Когда просто смотришь на все эти шаги, кажется, что это просто свалка из Кучи Разных Странно Написанных Цифр. И запутаться во всём этом в первый раз – нормально. И во второй, и в третий. Просто попробуйте сделать это ещё и ещё раз – по шагам, как написано выше, и всё получится.
И наоборот это тоже работает! Например, число 110101012 – как из него сделать понятное десятичное? Точно так же, при помощи таблички. Пойдем с конца:
1*2 0 +0*2 1 +1*2 2 +0*2 3 +1*2 4 +0*2 5 +1*2 6 +1*2 7 =
Вот примерно так компьютер понимает привычные нам числа.

Итак, возьмем пример 15+6 и решим его в разных системах счисления. Понятно, что в нашей, десятичной, получится 21. А что выйдет, например, в восьмеричной?
Переводим 15 в восьмеричную систему счисления. Первый шаг у нас при переводе в другую систему – посмотреть в табличку степеней. 8 2 – это уже 64, и в 15 оно точно уже никак не влезет, поэтому берем 8 1 – то есть просто 8. 15–8=7, оно меньше нашего основания 8, поэтому с ним мы ничего не делаем.
Итак, получилось, что 15=8 1 +7.
В восьмеричной системе логика точно такая же, как, например, в двоичной: 8 3 – это 1000, 8 2 – это 100, 8 1 – это 10. Получилось, что:
Напомню, наш пример был 15+6. 15 мы перевели в восьмеричную систему, как же перевести 6? Она меньше 8, нашего основания, поэтому ответ – оставить как есть. Наш пример сейчас выглядит так:
Теперь мы будем складывать в восьмеричной системе счисления. Как это делается? Так же, как и в десятичной, но надо помнить, что десяток в восьмеричной системе – это восемь, а не десять, и что 8 и 9 в ней не существует.
Когда мы считаем в десятичной системе, по сути, мы делаем так:
15+6=15+5+1=20+1=21
Попробуем проделать тот же фокус в восьмеричной системе:
Почему 17+1? Потому что 7+1=8, а 8 – это наш десяток! В восьмеричной системе 7+1=10, а значит, 17+1=20. Если на этом месте ваш мозг начинает бить тревогу и рассказывать, что здесь что-то не так, вернитесь в начало статьи, где мы с вами считали в разных системах счисления.
Теперь наш пример выглядит как
Переведем 258 обратно в нашу систему счисления. В десятичной мы бы, увидев число 25, могли сказать, что в нём две десятки и пять единиц. В восьмеричной, как вы, наверное, уже догадались, число 258 – это две восьмерки и пять единиц. То есть 258=2*8+5=2110.
Итак, наш пример целиком:
Получилось точно такое же 21, какое вышло у нас в самом начале, когда мы посчитали 15+6 привычным нам способом в десятичной системе.
Арифметические правила не меняются от того, что мы выбрали другую систему счисления.
Поэтому и компьютер, переводя всё в нули и единицы, которые для нас выглядят непонятно и бессмысленно, не теряет при этом информацию, которую мы ему дали, и может, посчитав в удобной ему форме, выдать результат, переведя его обратно в привычный нам вид.
Задачи:
- рассмотреть десятичную систему счисления как частный случай системы построения многозначного числа;
- вести работу по формированию у детей умения строить величину по данному числу и системе мер;
- формировать умение строить систему мер в заданной системе счисления;
- осваивать переход к новому позиционному способу записи многозначного числа;
- повторить известные детям величины и их мерки;
- развивать внимание, мышление учащихся;
- способствовать формированию у учащихся умения работать в группе (в паре);
- формировать детскую самооценку, взаимооценку до и после выполнения задания по совместно выработанным критериям оценивания.
Оборудование:
- изображение чашек и блюдец сервиза с примерами на каждом предмете;
- карточки с названиями величин и их мерок (на каждую группу);
- карточки с текстами рецепта заваривания чая (на каждую группу);
- изображение конфет на магнитной основе для работы у доски;
- карточки с числами до 10 для подвижной игры;
- индивидуальные наборы из трех украшений торта для проведения рефлексии урока.
Ход урока.
Минутка создания настроения и разминки пальчиков. Соприкасаемся пальчиком с соседом по парте и говорим:
желаю (большой)
успеха (указательный)
большого (средний)
во всем (безымянный)
и везде (мизинец).
Здравствуй (вся ладонь).
“Здравствуйте”, — ты скажешь человеку.
“Здравствуй”, — улыбнется он в ответ.
И, наверное, не пойдет в аптеку,
И здоровым будет целый век.
Сегодня у нас на уроке гости. Как вы думаете, с какой целью они пришли? Чем вы хотите их удивить? Вы волнуетесь? Урок пройдет успешно?
Устные упражнения на доске.
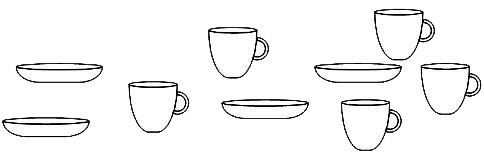
Фронтальная работа с индивидуальной проверкой. Составим пары, решив примеры. (Одной чашечке не хватает блюдца).
Составьте пример перехода через десяток с ответом 14.
На полочке есть три блюдца, какое выбрать? Докажите. 15+1 7+7 11+3
Сервиз готов, пора и чай заваривать. Но дело это не простое. Не зря говорят: “Чай заваривать – не дров нарубить”. Тут наука нужна, без величин не обойдешься.
Прочитать рецепт заваривания чая, определить какая математическая величина участвует в нем.
В литровый чайник засыпать щепотку чая и добавить несколько капель воды. Все перемешать. Добавить снова щепотку чая и еще немного воды; все повторять до тех пор, пока чайник не станет полным. (Объем).
Докажите. (Речь идет о вместимости, мерки – щепотка, литр).
Чтобы двигаться дальше, вспомним и о других величинах и их мерках.
Работа в группах.
Восстановить список величин:
- масса ( );
- … (см, дм, км);
- количество ( , пара);
- … (литр );
- … ( );
- площадь ( ).
Проверка. Обмен работами между группами.
Оценивание: по правильности, по сложности работы в группе.

1. Построение величины по числу и системе мер.
Любят взрослые и детки
Всевозможные конфетки.
Кто грызет, а кто глотает,
Кто за щечкою катает.
В вазочку положим конфеты.

- В какой системе счисления построены мерки? (Троичная).
- Докажите. (Вторая мерка состоит из трех первых; третья – из трех вторых).
- Назовите основную мерку. (К1).
- Как называются мерки К2, К3? (Дополнительные).
- Начинаем сыпать конфеты? (Нет, числа не хватает).
- Ищем число.
2. Посмотрите и решите, какое задание для вас приготовлено. Найти одинаковые числа в таблице и в строке.
| 11(3) | III | II | I |
| 102(3) | 1 | 2 | (4) |
| 122(3) | 1 | 1 | (3) |
| 102(4) | 1 | 1 | (3) |
| 120(4) | 1 | 2 | (3) |
| 101(3) | 1 | 2 | (4) |
122(3) – “лишнее” число.
По нему и будем строить величину М. Что показывает каждая цифра в этом числе? От чего зависит значение цифры? (От места в записи числа).
Самооценка до начала работы: сможешь ли ты выполнить это задание?
Самостоятельное построение величины. Один ученик у доски.
Оценивание. Можно ли принять эту работу за образец правильности? Оцените свою работу по правильности.
1. В разных системах счисления мы измеряли и строили величины, но одну из них не использовали. Какую? (Десятичную). Не возникает ли в связи с этим у вас вопроса? (Да, возникает, почему так?)
Запишем вопрос: Почему десятичную систему изучаем отдельно?
Посчитаем те же конфеты в десятичной системе счисления. Что это значит? (Считаем до 10, результат: 17(10)).
Пирожки румяные
До того нарядные!
Мы не сразу их съедим,
Понаблюдаем, поглядим.
Работа с учебником с.88 №268.
Измерить в пятеричной системе – взаимопроверка в парах, в десятичной системе – с комментированием.
Дорога за тортом (результат – 57).
Чем же “знаменита” десятичная система счисления? (Вопрос остается).
Муниципальное бюджетное общеобразовательное учреждение
Конспект урока математики во 2 "б" классе
Тип урока: интегрированный урок отработки открытого способа.
Программа: развивающее обучение по системе Д. Б. Эльконина – В. В. Давыдова.
Выполнила
учитель начальных классов
Делавина Ольга Викторовна
Стаж работы по специаль -
Арзамас – 2018 год.
Цель: Закрепить вычислительные навыки в концентре "Тысяча"; познакомить учащихся с некоторыми произведениями, предлагаемыми для внеклассного чтения; способствовать развитию вычислительных навыков, интереса к художественной литературе, расширению кругозора учащихся; содействовать воспитанию бережного отношения к природе, книге.
Оборудование. Книги: Лазарь Лагин. "Старик Хоттабыч", Дж. Родари. "Приключения Чиполлино", Редьярд Киплинг. "Маугли", Алексей Толстой. "Приключения Буратино. ", Даниель Дефо. "Робинзон Крузо"; грамзапись "Страна Литературия", магнитофонная запись "Я веселый Чиполлино"; картинки с изображением пантеры и удава; карточки с буквами; карточки с заданиями; мультимедийный проектор.
Структура урока Хронометраж
I. Мотивационно – оценочный 3 мин
1. Актуализация знаний 1 мин
2. Ситуация успеха 2 мин
II. Исполнительный 30 мин
1. Проверка домашнего задания 4 мин
2. Решение примеров 5 мин
3. Физкультминутка 2 мин
4. Упражнение в записи и решении уравнений 5 мин
5. Системы счисления 10 мин
6. Физкультминутка 2 мин
7. Решение задач 5 мин
8. Домашнее задание 2 мин
III. Итог урока. Рефлексия 2 мин
ХОД УРОКА
I. Мотивационно-оценочный (3 мин)
1. Актуализация знаний (1 мин)
СЛАЙД №1.
Учитель: Встали. Улыбнулись друг другу. Улыбнулись мне. Сели на места.
2. Ситуация успеха (2 мин)
СЛАЙД № 2.
Учитель: А что мы должны знать и уметь, чтобы решить задачу?
Определять часть и целое;
Помнить о ловушках.
Учитель: А что мы должны знать, чтобы решить уравнение?
Определять часть и целое.
Учитель: С чем вы можете справиться хорошо? (ответы детей)
Учитель: А где испытываете затруднения? (ответы детей)
Учитель: Вот этим мы сегодня и займемся. И к концу урока, я думаю, вы уже лучше будете справляться с трудностями. Сегодня на уроке математики мы совершим путешествие в страну литературных героев.
СЛАЙД № 3
Звучит грамзапись "Страна Литератури я".
II. Исполнителный (30 мин)
1. Проверка домашнего задания (4 мин)
Учитель: Первым нас встречает "тощий и смуглый старичок с бородой по пояс, в роскошной чалме, тонком белом шерстяном кафтане, обильно расшитом золотом и серебром, в белоснежных шелковых шароварах и нежно-розовых сафьяновых туфлях с высоко загнутыми носками". Вольке Костылькову он представился как джинн Гассан Абдуррахман ибн Хоттаб.
Учитель : Кто это? СЛАЙД № 4
Дети: Старик Хоттабыч
Учитель: Мальчик помог ему освободиться из замшелого глиняного сосуда, похожего на древнюю амфору. Поэтому старик решил быть слугой мальчика. Волька выполнял дома № на с., а Хоттабыч освободил его от необходимости долго думать: выдернул из своей бороды волосок, прошептал заклинание – и вот что оказалось в Волькиной тетради.
Х + 85 = 185 х + 100 = 200 300 – х = 250
Учитель: Так ли записаны выражения у вас?
Учащиеся исправляют ошибки в первом и третьем примерах
Дети: В первом примере будет ответ 100 (100; 50) .
Учитель: Кто назовет автора этой книги?
Если дети не знают, учитель показывает книгу, дети читают фамилию автора, открывается карточка около фамилии Лагин.
2. Решение примеров (5 мин)
Учитель : А это кто нам машет рукой?
У сеньора Помидора льются слезы от позора.
Не хватай за чубчик длинный и не трогай …
Дети: Чиполлино! СЛАЙД № 5
Звучит грамзапись "Я веселый Чиполлино".
285 – Редьярд Киплинг
350 – Астрид Линдгрен
185 – Джани Радари
3. Физкультминутка (2 мин) СЛАЙД № 6.
Учитель: Принц Лимон и сеньор Помидор заточили в подземелье дедушку Чиполлино, дядюшку Тыкву, музыканта Грушу и других жителей сказочного города. Чтобы открыть замок в темнице, Чиполлино и его друзья должны разгадать код сеньора Помидора. А братья и сестры Чиполлино решили помочь ему. Запишем примеры в столбик и решим их.
374 + 526 4840 - 2800 6408 + 2422
Дети выполняют проверку в тетрадях, а два ученика – на индивидуальных досках для дальнейшей проверки с классом.
4. Упражнение в записи и решении уравнений (5 мин)
Учитель: А вот вдалеке мальчик, волею судьбы оказавшийся в диких джунглях и выросший в волчьей стае. Его друзьями были медведь Балу, удав Каа, пантера Багира, а злейшим врагом – тигр Шер-хан.
Учитель: Кто узнал этого мальчика? СЛАЙД № 7.
Дети: Это Маугли
Учитель: Давайте побольше узнаем о его друзьях. Для этого решим задачи.
СЛАЙД № 8.
Длина прыжка пантеры – Х м. если ее уменьшить на 7 м, то получится длина прыжка тигра – 5 м. Узнай длину прыжка пантеры.
Отрывок читает ученик.
Дети: "Багира, черная пантера, черная вся сплошь, как чернила, но с отметинами, которые, как у всех пантер, видны на свету. Все в джунглях знали Багиру, и никто не захотел бы становиться ей поперек дороги, ибо она была хитра, отважна. бесстрашна. Зато голос у нее был сладок, как дикий мед, капающий с дерева, а шкура мягче пуха".
Показ иллюстрации пантеры
Учитель: Если длину тела удава Каа – 9 м – уменьшить на Х м, то получим длину тела Багиры с длиной ее хвоста – 3 м. Узнайте, на сколько метров длина тела Багиры с длиной ее хвоста меньше длины тела Каа.
Показ иллюстрации удава.
х = 3 м - разница
Ответ: на 3 метра.
– Кто автор книги "Маугли"? СЛАЙД № 9.
Учитель открывает карточку около фамилии Киплинг. Выставляет книгу.
5. Системы счисления (5 мин) СЛАЙД № 10.
Учитель: Как вы знаете, Незнайка побывал в Солнечном городе и даже на Луне.
Учитель: Коротышки в Солнечном городе могли считать только до 3. Какая это система счисления? (Троичная)
Учитель: Лунатики могли считать до 5 – какая система? (Пятеричная)
Учитель: Посчитайте предметы сначала в троичной, а потом в пятеричной системах счисления.
С = 122 (3) Л = 32 (5)
Учитель: Кто назовет автора книги о Незнайке и его друзьях? (Н. Носов)
6. Физкультминутка (2 мин) СЛАЙД № 11.
7. Решение задач (5 мин)
Учитель: А это кто идет нам навстречу? СЛАЙД № 12.
Деревянным острым носом
Всюду лезет он без спросу.
Даже дырку на картине
Учитель: За рассказ о потайной двери в каморке старого папы Карло Буратино получил от Карабаса Барабаса 5 золотых монет. Лиса Алиса и кот Базилио привели Буратино на пустырь. "Это поле чудес, – сказали они. – Если закопаешь золотые монеты, то наутро вырастет дерево, на котором будет на 135 золотых монет больше ". Сколько монет должно быть на дереве?
Дети. 5 + 135 = 140 (монет).
Учитель: А сейчас вам предстоит решить задачу и помочь Буратино и его друзьям спастись от Карабаса Барабаса.
1) 25 + 15 = 40 (мин) – потребуется Буратино.
2) 25 + 40 = 65 (мин) – потребуется Карабасу.
Ответ: 65 мин или 1час 5 минут.
Учитель: Назовите автора.
СЛАЙД № 13.
Учитель открывает карточку около фамилии Толстой. Выставляет книги
8. Домашнее задание (2 мин) СЛАЙД № 14.
Учитель: А вот еще один литературный герой. Это мужчина в английском платье ХVIII в. Однажды корабль, на котором он плыл, потерпел крушение, и человек оказался на необитаемом острове. Там он прожил в одиночестве много лет, затем подружился с туземцем и назвал его Пятницей. О ком идет речь?
Учитель: Назовите автора книги.
Дети: О Робинзоне Крузо.
Учитель: Однажды Робинзон Крузо обнаружил около пещеры, где жил, 32 колоска ячменя, ржи – на 18 колосков больше, а пшеницы столько, сколько ячменя и ржи вместе. Сколько колосков пшеницы нашел Робинзон?
Учитель: Эту задачу я предлагаю вам решить дома.
Дети: Даниэль Дефо
Учитель открывает карточку около фамилии Дефо. Выставляет книгу
III. Итог урока (2 мин)
Учитель: Какие литературные герои помогли нам повторить изученный материал?
СЛАЙД № 15.
Дети: Хоттабыч, Чиполлино, Маугли, Буратино, Робинзон Крузо
Учитель: Кто нам рассказал о них? (СЛАЙД № 16.) Прочитайте фамилии авторов, записанные на доске.
На доске: Лазарь Лагин, Джанни Родари, Редьярд Киплинг, Алексей Толстой, Николай Носов, Даниэль Дэфо.
Учитель: А теперь я хочу спросить вас: лучше ли вы стали понимать изученный материал?
Учитель: За работу на уроке я ставлю оценки….
Приложение № 1.
Однажды Робинзон Крузо обнаружил около пещеры, Однажды Робинзон Крузо обнаружил около пещеры
где жил, 32 колоска ячменя, ржи – на 18 колосков где жил,32 колоска ячменя, ржи - на 18 колосков
больше, а пшеницы столько, сколько ячменя и ржи больше, а пшеницы столько, сколько ячменя и ржи
вместе. Сколько колосков пшеницы нашел Робинзон? вместе. Сколько колосков пшеницы нашел Робинзон?
Самоанализ интегрированного урока
Поставленные обучающие, развивающие и воспитательные задачи соответствуют возрастным особенностям учащихся и уровню развития класса.
Форма проведения урока – урок – путешествие по Стране Литературии. Выбранная мной структура урока и его содержание рациональны для решения поставленных задач.
На данный момент дети умеют: решать задачи различных типов в одно, два и три действия; составлять уравнения и решать их; выполнять счет в различных системах счисления; складывать и вычитать многозначные числа столбиком; владеют навыками устного счета в пределах ста.
Исходя из темы урока мною были спланированы три учебно – воспитательные цели. Обучающий аспект: закрепление и повторение изученных типов задач, уравнений, систем счисления, случаев сложения и вычитания многозначных чисел. Образовательный аспект: развитие познавательного интереса. В плане воспитательного аспекта я обозначила задачи: воспитывать чувство взаимоуважения и взаимовыручки, формировать умение работать в коллективе, воспитывать бережное отношение к природе, книге.
На первом этапе (Актуализация знаний) я выделяю три пункта:
вхождение в контакт (настрой на работу при помощи улыбок);
ситуация успеха (чему научились и чему должны научиться);
рефлексия (повторение изученного материала).
На втором этапе (Операционно - исполнительный) я отрабатывала с детьми открытый способ действия с многозначными числами, системами счисления, умение решать задачи и уравнения. К доске старалась вызывать детей, наиболее часто допускающих ошибки с целью коллективного нахождения и исправления.
Удачей считаю следующее:
- дети могут определить, что они умеют делать хорошо, а что – недостаточно хорошо;
- не стесняются говорить о своих трудностях.
На третьем этапе (Рефлексивно - оценочный) дети пытались дать себе объективную оценку.
Над развитием речи я работала на протяжении всего урока, требуя строить правильные, полные ответы. Дифференцированный подход к каждому ученику помог почувствовать уверенность в своих силах. Использование на уроке физкультминуток снимало физическое напряжение и было направлено на сохранение здоровья детей и активизацию мыслительной деятельности.
Оборудование и наглядность подобраны в соответствии с целью и задачами урока.
При выборе приемов работы на уроке в качестве приоритетных я выбрала: образность, эмоциональность, последовательность, связность, доступность.
Атмосфера на уроке была эмоционально спокойная.
Поставленные цели и задачи на уроке были реализованы.
Аннотация к уроку.
Учитель: Делавина О. В., учитель начальных классов МБОУ СШ № 2 им. А. С. Пушкина,
стаж работы – 29 лет.
Тип урока: интегрированный урок отработки открытого способа.
Тема: Повторение (уравнения, задачи, системы счисления).
Образовательные: 1) закрепить и повторить сложение и вычитание в пределах 1000;
2) повторить системы счисления;
3) повторить решение уравнений и задач;
4) познакомить с некоторыми произведениями, предлагаемыми для внеклассного
5) способствовать развитию вычислительных навыков, интереса к художественной
Развивающие: 1) развивать логическое мышление, память, интерес к чтению;
2) работать над развитием устной речи;
3) развивать стремление научиться лучше и быстрее считать;
4) развивать активную познавательную деятельность через игры, логические задания;
5) развивать способность к обобщению, систематизации полученных знаний.
Воспитательные: 1) воспитывать чувства взаимоуважения и взаимопомощи;
2) формировать умение работать в коллективе;
3) воспитывать бережное отношение к природе, книге;
4) воспитывать рациональность в учебно-познавательной деятельности.
Здоровьесберегающие: 1) проводить профилактику умственного перенапряжения путем смены видов
2) поддерживать атмосферу психологического благополучия и учебной
Оборудование: - книги и портреты писателей;
- картинки с изображениями героев произведений;
- карточки с заданиями;
- карточки с домашним заданием;
На уроке Вы можете увидеть: 1) практическую значимость изучаемого материала;
2) формирование навыка установления причинно – следственных связей;
3) использование материала, направленного на повышение мотивации
к изучению темы;
4) создание атмосферы психологического успеха и морального
удовлетворения собственными успехами;
5) приемы формирования устойчивого интереса;
6) использование интеграции.
| delavina-o-v-urok-matematiki-povtorenie-uravnenija-zadachi-sistemy-schislenija_1pt26.ppt | 1328,5 Кб |
Урок математики в 3 классе по программе Аооп уо Муниципальное бюджетное общеобразовательное учреждение «Специальная (коррекционная) общеобразовательная школа для обучающихся с ограниченными.
Читайте также:


