Предположим что надежность определения туберкулеза при рентгеновском

На формулу полной вероятности и формулу Байеса.

25.1. В урне лежит шар неизвестного цвета – с равной вероятностью белый, черный или красный. В урну опускается один белый шар и после перемешивания наудачу извлекается один шар. Он оказывается белым. Какова вероятность того, что в урне остался белый шар?

25.2. Имеются две партии деталей, в одной из которых все детали удовлетворяют техническим условиям, а в другой 25% деталей бракованные. Взятая наудачу деталь оказалась доброкачественной . Какова вероятность того, что она была взята из первой партии?

25.3. В первой урне имеется 3 белых и 4 черных шара, во второй 5 белых и 3 черных. Из первой урны наугад берутся 2 шара, из второй 1 шар. Эти три шара помещают в третью, пустую урну. После этого из третьей урны вынимают 1 шар. Найти вероятность того, что этот шар белый.

25.4. При проверке качества зерен пшеницы было установлено, что все зерна могут быть разделены на 4 группы: к зернам 1 группы принадлежат 96%, ко 2-й – 2%, к -3-й-1%, к 4-й-1% всех зерен. Вероятность того, что из зерна вырастет колос, содержащий не менее 50 зерен для семян 1 группы равна 0,5, для 2 группы – 0,2, для 3 группы – 0,18, для 4-0,02. Определить вероятность того, что из взятого наудачу зерна вырастет колос, содержащий не менее 50 зерен.

25.5. Предположим, что надежность определения туберкулеза при рентгеновском просвечивании грудной клетки составляет 90% (т.е. 10% носителей туберкулеза остаются неопознанными). Вероятность того, что у здорового человека будет ошибочно определен туберкулез, составляет 1%. Просвечиванию была подвергнута большая группа людей со средним % больных, равным 0,1%. Какова вероятность того, что человек, признанный больным, действительно является носителем туберкулеза.

25.6. Внутри квадрата с вершинами (0,0); (0,1); (1,0); (1,1) наудачу выбирается точка М(х,у). Найти вероятность события А, состоящего в том, что max(x,y)0.

25.7. В коробке находятся две неотличимые игральные кости: правильная и неправильная, у которой шестерка выпадает с вероятностью 1/3, единица – 1/9, остальные с одинаковой вероятностью. Наудачу взятая из коробки кость была брошена и выпало k очков. Найти вероятность pk того, что была подброшена правильная игральная кость, если : а) k=1, б)k=6, в)k=5.

25.8. Имеются две партии деталей, в одной из которых все детали удовлетворяют техническим условиям, а в другой 25% деталей бракованные. Взятая наудачу деталь оказалась доброкачественной. Какова вероятность того, что она была взята из первой партии?

25.9. Исследование больного вызвало предположение о возможности одного из трех заболеваний А1, А2, А3 с вероятностями: Р(А1)=5/12, Р(А2)=1/3, Р(А3)=1/4. Для уточнения диагноза был произведен некоторый анализ, который при первом заболевании дает положительный ответ с вероятностью 0.8; при втором – 3/8; при третьем – 1/6. Анализ дал положительный результат. Какова после этого вероятность каждого из трех заболеваний?

25.10. Вероятность наступления после ясного дня опять ясного дня равна P1. Вероятность наступления после пасмурного дня снова пасмурного дня равна P2. Сегодня ясно. Какова вероятность того, что послезавтра будет: а) ясно; б) пасмурно.

25.11. По линии связи возможно передача кода 1234 с вероятностью 0,6 и кода 4321 с вероятностью 0,4. Код высвечивается на табло, которое может исказить цифры. Вероятность принять 1 за 1 равна0,8; а 1 за 4 равна 0,2. Вероятность принятия 4 за равна 0,9; а 4 за 1 равна 0,1. Вероятность принятия 2 за 2 и 3 за 3 равна 0,7. Вероятность принятия 2 за 3, а 3 за 2 равна 0,3. Оператор принял код 4231. Определить вероятность того, что передан код: а) 1234; б) 4321.

25.12. В ящике лежат 20 теннисных мячей, в том числе 15 новых и 5 играных. Для игры наудачу выбирается два мяча и после игры возвращаются обратно. Затем для второй игры также наудачу извлекаются еще два мяча. Какова вероятность того, что вторая игра будет проводиться новыми мячами?

25.13. На фабрике машина № 1 производит 40% всей продукции, остальную часть продукции производит машина №2. Брак в продукции машины №1 составляет 0,9%, а в продукции машины №2 – 0,4%. Взятая наудачу деталь оказалась бракованная. Найти вероятность того, что она сделана на машине № 1.

25.14. Брак в продукции завода вследствие дефекта А составляет 5%, причем среди забракованной продукции по признаку А в 10% случаев встречается дефект В, а в продукции свободной от дефекта А, дефект В встречается в 1% случаев. Найти вероятность того, что дефект В не встретится во всей продукции.

25.15. По линии связи возможна передача кода 1234 с вероятностью 0.6 и кода 4321 с вероятностью 0.4 . Код высвечивается на табло, которое может исказить цифры. Вероятность принять 1 за 1 равна 0.8, а 1 за 4 равна 0,2.Вероятность принятия 4 за 4 равна 0,9, а 4 за 1 равна 0,1. Вероятность принятия 2 за 2 и 3 за 3 равна 0,7. Вероятность принятия 2 за 3, а 3 за 2 равна 0,3. Оператор принял код 4231. Определить вероятность того, что передан код: а)1234; б) 4321.

25.16. В партии 600 лампочек: 200 штук изготовлены на 1-ом заводе, 250 – на 2-ом, 150 – на 3-ем. Вероятность того, что лампочка окажется стандартной для 1-го завода равна 0,97; для 2-го – 0,91; для 3-го – 0,93. Какова вероятность того, что наудачу взятая лампочка, оказавшаяся стандартной, изготовлена на 1-ом заводе?

25.17. Две перфораторщицы набили по одинаковому комплекту перфокарт. Вероятность того, что 1-ая перфораторщица допустит ошибку, равна 0,1; для второй перфораторщицы эта вероятность равна 0,2. При сверке перфокарт была обнаружена ошибка. Найти вероятность того, что ошиблась вторая перфораторщица.

25.18. В урне лежит шар неизвестного цвета – с равной вероятностью белый, черный или красный. В урну опускается один белый шар и после перемешивания наудачу извлекается один шар. Он оказывается белым. Какова вероятность того, что в урне остался белый шар?

25.19. Имеются две партии деталей, в одной из которых все детали удовлетворяют техническим условиям, а в другой 25% деталей бракованные. Взятая наудачу деталь оказалась доброкачественной . Какова вероятность того, что она была взята из первой партии?

25.20. В первой урне имеется 3 белых и 4 черных шара, во второй 5 белых и 3 черных. Из первой урны наугад берутся 2 шара, из второй 1 шар. Эти три шара помещают в третью, пустую урну. После этого из третьей урны вынимают 1 шар. Найти вероятность того, что этот шар белый.

25.21. При проверке качества зерен пшеницы было установлено, что все зерна могут быть разделены на 4 группы: к зернам 1 группы принадлежат 96%, ко 2-й – 2%, к -3-й-1%, к 4-й-1% всех зерен. Вероятность того, что из зерна вырастет колос, содержащий не менее 50 зерен для семян 1 группы равна 0,5, для 2 группы – 0,2, для 3 группы – 0,18, для 4-0,02. Определить вероятность того, что из взятого наудачу зерна вырастет колос, содержащий не менее 50 зерен.

25.22. Предположим, что надежность определения туберкулеза при рентгеновском просвечивании грудной клетки составляет 90% (т.е. 10% носителей туберкулеза остаются неопознанными). Вероятность того, что у здорового человека будет ошибочно определен туберкулез, составляет 1%. Просвечиванию была подвергнута большая группа людей со средним % больных, равным 0,1%. Какова вероятность того, что человек, признанный больным, действительно является носителем туберкулеза.

25.23. Внутри квадрата с вершинами (0,0); (0,1); (1,0); (1,1) наудачу выбирается точка М(х,у). Найти вероятность события А, состоящего в том, что max(x,y)0.

25.24. В коробке находятся две неотличимые игральные кости: правильная и неправильная, у которой шестерка выпадает с вероятностью 1/3, единица – 1/9, остальные с одинаковой вероятностью. Наудачу взятая из коробки кость была брошена и выпало k очков. Найти вероятность pk того, что была подброшена правильная игральная кость, если : а) k=1, б)k=6, в)k=5.

25.25. Имеются две партии деталей, в одной из которых все детали удовлетворяют техническим условиям, а в другой 25% деталей бракованные. Взятая наудачу деталь оказалась доброкачественной. Какова вероятность того, что она была взята из первой партии?

25.26. Исследование больного вызвало предположение о возможности одного из трех заболеваний А1, А2, А3 с вероятностями: Р(А1)=5/12, Р(А2)=1/3, Р(А3)=1/4. Для уточнения диагноза был произведен некоторый анализ, который при первом заболевании дает положительный ответ с вероятностью 0.8; при втором – 3/8; при третьем – 1/6. Анализ дал положительный результат. Какова после этого вероятность каждого из трех заболеваний?

25.27. Вероятность наступления после ясного дня опять ясного дня равна P1. Вероятность наступления после пасмурного дня снова пасмурного дня равна P2. Сегодня ясно. Какова вероятность того, что послезавтра будет: а) ясно; б) пасмурно.

25.28. По линии связи возможно передача кода 1234 с вероятностью 0,6 и кода 4321 с вероятностью 0,4. Код высвечивается на табло, которое может исказить цифры. Вероятность принять 1 за 1 равна0,8; а 1 за 4 равна 0,2. Вероятность принятия 4 за равна 0,9; а 4 за 1 равна 0,1. Вероятность принятия 2 за 2 и 3 за 3 равна 0,7. Вероятность принятия 2 за 3, а 3 за 2 равна 0,3. Оператор принял код 4231. Определить вероятность того, что передан код: а) 1234; б) 4321.

25.29. В ящике лежат 20 теннисных мячей, в том числе 15 новых и 5 играных. Для игры наудачу выбирается два мяча и после игры возвращаются обратно. Затем для второй игры также наудачу извлекаются еще два мяча. Какова вероятность того, что вторая игра будет проводиться новыми мячами?

25.30. На фабрике машина № 1 производит 40% всей продукции, остальную часть продукции производит машина №2. Брак в продукции машины №1 составляет 0,9%, а в продукции машины №2 – 0,4%. Взятая наудачу деталь оказалась бракованная. Найти вероятность того, что она сделана на машине № 1.

Две машины на некоторой фирме производят соответственно 10 и 90% общей продукции определенного вида. Предположим, что вероятность брака на первой машине равна 0,01, а на второй – 0,05. Чему равна вероятность того, что наугад взятое из дневной продукции изделие изготовлено первой машиной, если оно оказалось бракованным?

Применим теорему Байеса.
— событие, заключающееся в том, что изделие бракованное;
— изделие изготовлено первой машиной;
— изделие изготовлено второй машиной.
.

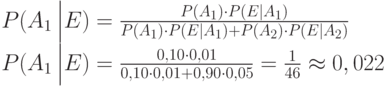
Предположим, что надежность определения туберкулеза при рентгеновском просвечивании грудной клетки составляет 90%, то есть 10% тбц-носителей остаются неопознанными; вероятность неправильного определения тбц у здоровых людей составляет 1%.

Просвечиванию была подвергнута большая группа людей со средним процентом больных 0,1%. Какова вероятность того, что люди, которые признаны больными, действительно являются тбц-носителями?

— просвечивание определило наличие тбц,
— человек болен,
— человек здоров.

,

то есть мы нашли, что из общего числа людей, признанных больными, только 8% являются действительно тбц-носителями.

В среднем рентгеновские исследования дают 30% неправильных отрицательных и 2% неправильных положительных диагнозов!

В бюро работают 4 секретарши, которые отправляют соответственно 40, 10, 30 и 20% исходящих бумаг. Вероятности ошибки при этом соответственно равны 0,01; 0,04; 0,06 и 0,01. Чему равна вероятность того, что некоторый документ неверно адресован третьей секретаршей?

Ничего себе, 39% всех ошибок!

В ряде случаев для обоснования решений представляется возможным провести несколько экспериментов. Очевидно, что с ростом экспериментов растет и надежность статистического решения, то есть уменьшается риск, связанный с принятием ошибочного решения. Однако постановка каждого эксперимента связана с определенным расходом средств. Более того, в ряде случаев просто нецелесообразно или невозможно провести все необходимые эксперименты для обоснования оптимального решения. Такие условия, например, складываются, когда необходимо принять партию взрывателей. Очевидно, для выбора решения, принять или не принять данную партию, можно проверить только часть взрывателей, так как проверка всей партии связана с их уничтожением.

На основании изложенного можно сформулировать следующие условия для обоснования оптимального решения при нефиксированных экспериментах.

Имеются некоторые действия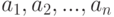
и состояния "природы"
. Требуется выбрать действие, которое соответствует истинному состоянию природы на основе оценки результатов эксперимента
из одного наблюдения,
из двух наблюдений, в котором
повторяется дважды,…,
из
наблюдений, в котором
повторяется
раз.

Затем определяется множество стратегий (правил решения)
. Любая стратегия из этого множества должна однозначно указывать до начала эксперимента, что нужно сделать на каждом этапе экспериментирования в зависимости от имеющейся информации. Каждому возможному исходу, обусловленному стратегией, присваивается показатель эффективности . Такой показатель должен учитывать стоимость данного исхода и потери, вызванные неправильными решениями. Вычисляется также и вероятность каждого исхода для истинного состояния "природы"
и стратегии
. Кроме того, для каждого состояния и каждой стратегии вычисляются потери или выигрыши, связанные с парами (" исход – состояние"), которые взвешены согласно вероятностям, вычисленным в предположении наличия данного состояния "природы". В результате каждая стратегия оценивается величинами средних потерь.

В жизни нередко складываются ситуации, когда необходимо принимать решение при отсутствии как полного и точного знания обстановки, так и возможности получения какой-либо дополнительной информации. С подобной неопределенностью мы уже сталкивались, рассматривая обоснование решений методами теории игр. Однако тогда неопределенность создавалась за счет скрытности выбора, осуществляемого противником. В результате этого (по крайней мере в антагонистических играх двух лиц) всегда можно предсказать поведение второго игрока, который стремится сделать все зависящее от него для противодействия первому игроку. Особенность же рассматриваемой неопределенности состоит в том, что второй игрок не является, строго говоря, противником. Часто таким вторым игроком оказывается "природа", и поэтому соответствующие задачи выбора оптимального способа действий с помощью теории статистических решений иногда называют играми против природы. С этой точки зрения эта часть теории статистических решений имеет дело с так называемым случаем полного незнания, то есть такого случая, когда игрок, принимающий то или иное решение, не располагает никакими сведениями о конкретном состоянии природы. Если же игрок располагает даже небольшой информацией, скажем, полученной при том или ином эксперименте, то условия полного незнания оказываются нарушенными, и следует обратиться к вышеизложенным положениям теории статистических решений. Однако было бы ошибочно полагать, что случай полного незнания исключает наличие всякой информации. Здесь так же, как и в теории игр, необходим такой объем информации об обстановке, который позволяет построить матрицу игр, то есть считается, что игрок знает все стратегии, которые он может использовать сам, и стратегии (состояния) "природы". Кроме того, предполагается, что игрок знает все элементы матрицы эффективности.

Таким образом, единственное, но весьма существенное различие между проблемами теории игр и теории статических решений состоит в том, что "природа" в отличие от разумного игрока характеризуется стихийностью, а не сознательностью выбора. Иными словами, "природа" выбирает то или иное состояние без какого-либо намерения помешать игроку достичь своей цели наилучшим образом. Это различие нельзя переоценить, так как оно ( в отличие от теории игр) приводит к нескольким конкурирующим критериям оптимальности, используемым в теории статистических решений.

1.136. Из урны, содержащей 6 белых и 4 черных шаров, наудачу и последовательно извлекают по одному шару до появления черного шара. Найти вероятность того, что при­дется производить четвертое извлечение, если выборка производится: а) с возвращением; б) без возвращения.

а) Установить, зависимы или независимы следующие пары событий: А и В, А и F, F и В; б) вычислить вероятности событий BF, AF и ABF, используя формулу умножения вероятностей.

Вероятности сложных событий.

В следующих задачах приведены схемы соединения эле­ментов, образующих цепь с одним входом и одним выходом. Предполагается, что отказы элементов являются независи­мыми в совокупности событиями. Считается известной на­дежность p_k k-ro элемента (соответственно q_k = 1 — p_k — вероятность его отказа). Отказ любого из элементов приво­дит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вычислить надежность р каждой из схем.

Формула полной вероятности.

1.175. Прибор, установленный на борту самолета, может работать в двух режимах: в условиях нормального крейсер­ского полета и в условиях перегрузки при взлете и посадке. Крейсерский режим полета осуществляется в 80 % всего времени полета, условия перегрузки — в 20 %. Вероят­ность выхода прибора из строя за время полета в нормаль­ном режиме равна 0,1, в условиях перегрузки — 0,4. Вы­числить надежность прибора за время полета.

1.182. Три стрелка, вероятности попадания которых при одном выстреле в мишень в неизменных условиях постоян­ны и соответственно равны p₁ == 0,8,

р₂ = 0,7, р₃ = 0,6, делают по одному выстрелу в одну и ту же мишень. Вычис­лить вероятность события А == <в мишени окажется ровно две пробоины>, приняв в качестве гипотез элементарные исходы данного эксперимента.

1.184. В первой урне находится 6 белых и 4 черных шара, во второй — 3 белых и 2 черных. Из первой урны наудачу извлекают сразу 3 шара, и шары того цвета, кото­рые окажутся в большинстве, опускают во вторую урну и тщательно перемешивают. После этого из второй урны наудачу извлекают один шар. Какова вероятность того, что этот шар белый?

1.185. Два цеха штампуют однотипные детали. Первый цех дает a % брака, второй — b %. Для контроля отобрано n₁ деталей из первого цеха и n₂ из второго. Эти n₁ + n₂ деталей смешаны в одну партию, и из нее наудачу извлекают одну деталь. Какова вероятность того, что она бракованная?

Формула Байеса.

1.194. Однотипные приборы выпускаются тремя заво­дами в количественном отношении п₁ : п₂ : n_{3 ,} причем ве­роятности брака для этих заводов соответственно равны p₁, p₂ и p_3. Прибор, приобретенный научно-исследователь­ским институтом, оказался бракованным. Какова вероят­ность того, что данный прибор произведен первым заводом (марка завода на приборе отсутствует)?

1.196. На вход радиолокационного устройства с вероят­ностью 0,8 поступает смесь полезного сигнала с помехой, а с вероятностью 0,2 — только помеха. Если поступает полезный сигнал с помехой, то устройство регистрирует наличие какого-то сигнала с вероятностью 0,7; если только помеха, — то с вероятностью 0,3. Известно, что устройство зарегистрировало наличие какого-то сигнала. Найти ве­роятность того, что в его составе есть полезный сигнал.

1.197. Предположим, что надежность определения тубер­кулеза при рентгеновском просвечивании грудной клетки составляет 90 % (т. е. 10 % носителей туберкулеза остаются неопознанными). Вероятность того, что у здорового чело­века будет ошибочно определен туберкулез, составляет 1 %. Просвечиванию была подвергнута большая группа людей со средним процентом больных, равным 0,1 %. Какова вероятность того, что человек, признанный больным, дей­ствительно является носителем туберкулеза?

1.198. Прибор состоит из двух последовательно вклю­ченных узлов. Надежность (вероятность безотказной работы в течение времени T) первого узла равна 0,9, второго — 0,8. За время испытания прибора в течение времени Т зарегист­рирован отказ прибора. Найти вероятности следующих со­бытий: A₁ = <отказал только первый узел>, A₂ = <отка­зали оба узла>.

1.202. Три стрелка производят по одному выстрелу в од­ну и ту же мишень. Вероятности попадания в мишень при одном выстреле для каждого из стрелков соответственно равны p₁, р₂ и р₃. Какова вероятность того, что второй стре­лок промахнулся, если после выстрелов в мишени оказа­лось две пробоины?

1.203. В группе из 25 человек, пришедших сдавать экза­мен по теории вероятностей, имеется 10 отличников, 7 под­готовленных хорошо, 5 — удовлетворительно и 3 человека плохо подготовлены. Отличники знают все 25 вопросов про­граммы, хорошо подготовленные — 20, подготовленные удовлетворительно — 15, и плохо подготовленные знают лишь 10 вопросов. Вызванный наудачу студент ответил на два заданных вопроса. Найти вероятности следующих со­бытий: S₁ = <студент подготовлен отлично или хорошо>, S₂ = <студент подготовлен удовлетворительно>, S₃ = <сту­дент подготовлен плохо>.

1. Расспрос и физикальные методы исследования позволяют:

1) заподозрить туберкулез;

2) исключить туберкулез;

3) верифицировать диагноз туберкулеза;

4) установить массивность бактериовыделения;

5) исключить возможность сочетания туберкулеза с ВИЧ-инфекцией.

2. Более ранним признаком туберкулеза является:

2) кашель с мокротой;

4) боль в грудной клетке при дыхании;

5) повышение температуры тела до 37-37,4 °С 2-3 раза в неделю.

3. Пальпацию грудной клетки проводят для определения:

1) ритма дыхания;

2) нижних границ легких;

3) подвижности нижних краев легких;

4) характера дыхания;

5) голосового дрожания.

4. У больных с начальными проявлениями туберкулеза легких при осмотре обычно отмечают:

1) дистрофические изменения кожи;

2) расширенные межреберные промежутки;

3) крыловидные лопатки;

4) отсутствие каких-либо видимых патологических изменений;

5) дефицит массы тела.

5. Перкуссию легких проводят для определения:

1) ритма дыхания;

2) побочных дыхательных шумов;

3) подвижности нижних краев легких;

4) характера дыхания;

5) голосового дрожания.

6. Аускультацию легких проводят для определения:

1) глубины дыхания;

2) подвижности нижних краев легких;

3) характера дыхания;

4) голосового дрожания;

5) патологического ритма дыхания.

7. Туберкулин содержит:

1) L-формы возбудителя туберкулеза;

2) все антигенные компоненты МБТ;

3) отдельные антигенные компоненты возбудителя туберкулеза;

4) убитые М. bovis;

5) антитела к МБТ.

8. Ответная реакция на PPD-S и PPD-L более специфична, поскольку эти препараты не содержат:

1) липидных фракций и нуклеиновых кислот МБТ;

3) полисахаридов МБТ;

4) стабилизаторов и антисептиков;

9. Выявить специфическую аллергию к МБТ позволяет:

1) общий анализ крови;

2) рентгенография легких;

3) микроскопическое исследование бронхиального содержимого;

10. Внутрикожное введение туберкулина:

1) у неинфицированного МБТ человека может привести к заболеванию туберкулезом;

2) у инфицированного МБТ человека вызывает формирование в месте введения папулы;

3) у неинфицированного МБТ человека вызывает формирование в месте введения папулы;

4) у неинфицированного МБТ человека позволяет выявить отрицательную анергию;

5) у инфицированного МБТ человека позволяет выявить положительную анергию.

11. У инфицированного МБТ человека в месте внутрикожного введения 2 ТЕ обычно формируется:

3) участок депигментации;

5) участок гиперпигментации.

12. Пробу Манту обычно применяют с целью:

1) уточнения локализации туберкулезного поражения;

2) проведения массовой туберкулинодиагностики;

3) подтверждения наличия деструкции в зоне туберкулезного поражения;

4) определения биологического вида туберкулезного возбудителя;

5) подтверждения биологической трансформации МБТ в L-формы.

13. При пробе Манту с 2 ТЕ гиперергическая реакция на туберкулин у взрослых проявляется папулой размером не менее:

14. При пробе Манту с 2 ТЕ гиперергическая реакция на туберкулин у детей проявляется папулой размером не менее:

15. Результат внутрикожной туберкулиновой пробы Манту с 2 ТЕ оценивают, когда с момента введения туберкулина пройдет:

16. У впервые инфицированного МБТ ребенка после пробы Манту на месте папулы в дальнейшем нередко формируется:

1) звездчатый белесоватый рубчик;

2) линейный белесоватый рубчик;

3) участок депигментации;

5) участок гиперпигментации.

17. У вакцинированного БЦЖ ребенка отмечают переход поствакцинальной аллергии в инфекционную, если размеры папулы в месте введения 2 ТЕ, по сравнению с данными ранее проводимой пробы Манту:

1) увеличились на 2-3 мм;

2) увеличились на 6 мм и более;

3) увеличились не менее чем на 10 мм;

4) уменьшились на 2-3 мм;

5) остались без изменений.

18. Поствакцинальная аллергия маловероятна, если размеры папулы при пробе Манту с 2 ТЕ:

19. Наличие гиперергической реакции подтверждает появление в месте введения 2 ТЕ:

1) папулы размером 12-15 мм;

20. Отрицательная реакция на туберкулин у больного туберкулезом обусловлена:

1) положительной анергией;

2) приемом противотуберкулезных препаратов;

3) прекращением бактериовыделения;

4) отрицательной анергией;

5) закрытием полостей распада в легких.

21. Для решения вопроса о сохранении активности туберкулезного процесса более информативна проба:

1) Пирке со 100% туберкулином;

3) Манту с 10 ТЕ;

4) Манту с 100 ТЕ;

22. Противопоказанием для проведения пробы Манту с 2 ТЕ являются:

1) положительная реакция на пробу Манту в анамнезе;

2) кожные проявления экссудативного диатеза;

3) большие остаточные изменения после перенесенного туберкулеза;

4) пищевая аллергия;

5) туберкулез у других членов семьи.

23. Пробу Коха используют с целью:

1) диагностики первичного инфицирования МБТ;

2) выявления поствакцинальной аллергии;

3) определения резистентности к туберкулезной инфекции;

4) дифференциальной диагностики туберкулеза и других заболеваний;

5) выявления положительной анергии к МБТ.

24. Снижение чувствительности к туберкулину бывает при развитии:

3) хронического тонзиллита;

4) сахарного диабета;

25. Повышение чувствительности к туберкулину бывает при развитии:

3) хронического тонзиллита;

4) злокачественного новообразования;

26. В отличие от пробы Манту, тесты, основанные на определении гаммаинтерферона в крови:

1) позволяют установить повышенную чувствительность замедленного типа к МБТ;

2) позволяют диагностировать первичное инфицирование МБТ;

3) не приводят к усилению специфической сенсибилизации у инфицированных МБТ лиц;

4) не позволяют исключить устойчивость МБТ к лекарствам;

5) не позволяют обнаружить L-формы МБТ.

27. Микробиологическое исследование диагностического материала на МБТ имеет большое значение для подтверждения:

1) поствакцинальной аллергии;

2) природы патологического процесса;

3) виража чувствительности к туберкулину;

4) отрицательной анергии;

5) положительной анергии.

28. Для обнаружения МБТ в диагностическом материале его нужно окрасить методом:

29. Биологический вид микобактерий позволяет установить:

1) прямая микроскопия после окраски по Цилю-Нельсону;

2) прямая микроскопия после окраски по Шпенглеру;

3) прямая микроскопия после флотации;

4) люминесцентная микроскопия;

5) культуральное исследование.

30. Для исследования чувствительности МБТ к противотуберкулезным препаратам необходимо получить чистую культуру микобактерий методом:

1) прямой микроскопии с окраской по Цилю-Нельсону;

2) прямой микроскопии с окраской по Шпенглеру;

3) прямой микроскопии после флотации;

4) люминесцентной микроскопии;

31. Быстрым способом определения чувствительности МБТ к лекарствам является:

1) люминесцентная микроскопия;

2) исследование с использованием биологических микрочипов;

3) иммуноферментный анализ;

4) градуированная проба Пирке;

32. Наиболее информативный метод выявления фазы распада при туберкулезе легких:

2) магнитно-резонансная томография (МРТ);

3) боковая рентгенография;

5) компьютерная томография (КТ).

33. При туберкулезе органов дыхания из эндоскопических методов чаще используют:

34. Классическим местом для удаления жидкости из плевральной полости является:

1) первый-второй межреберный промежуток;

2) третий-четвертый межреберный промежуток;

3) пятый-шестой межреберный промежуток;

4) седьмой-восьмой межреберный промежуток;

5) нижний край IX ребра.

35. Для получения диагностического материала из стенки долевого бронха обычно проводят биопсию:

4) трансторакальную игловую;

36. При активном туберкулезе легких в общем анализе крови часто выявляют:

1) анемию и тромбоцитопению;

2) лейкопению и лимфоцитоз;

3) олигохромазию и анизоцитоз;

4) лейкоцитоз и лимфопению;

5) лейкоцитоз и моноцитопению.

37. Интегральным показателем для оценки функции внешнего дыхания являются:

1) показатели газового состава и кислотно-щелочного состояния крови;

2) данные спирографии;

3) результаты общей плетизмографии;

4) результаты капилляроскопии;

5) показатели остаточного объема легких.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой.