Правильные многогранники и вирусы

Урок на котором учащиеся закрепляют представление о правильных многогранниках и их применение в строении вирусов и бактерий, умение моделировать правильные многогранники из простых материалов и сопоставление изготовленной модели с природным аналогом .

Скачать:

Вложение	Размер
Урок "Правильные многогранники в геометрии"	2.9 МБ

Подписи к слайдам:

Схема расположения участников конференции

Приглашаю вас вернуться к прошлому занятию и перечислить понятия, которые нам необходимы для работы на уроке.

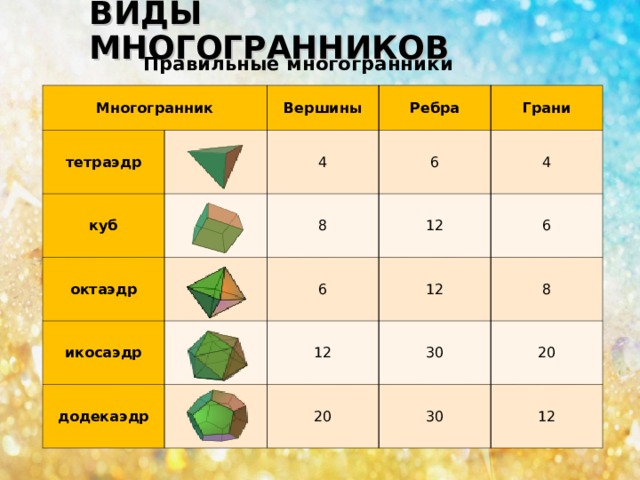
Тетраэдр Октаэдр Куб Додекаэдр Икосаэдр

В каких областях науки и практики нашли применение правильные многогранники?

Правильные многогранники в архитектуре

Правильные многогранники в генетике На микроскопическом уровне додекаэдр и икосаэдр являются относительными параметрами ДНК.Двойная нить спирали ДНК построена по принципу двухстороннего соответствия: за икосаэдром следует додекаэдр, затем опять икосаэдр и так далее. Это вращение через куб создает молекулу ДНК.

Правильные многогранники в географии Существует предположение о том, что двадцать районов планеты (вершины додекаэдра) являются центрами поясов выходящего вещества, основывающих биологическую жизнь (флора, фауна, человек).

Правильные многогранники в химии Кристаллы – тела, имеющие многогранную форму. Куб передает форму кристаллов поваренной соли ( NaCl ).

Правильные многогранники в химии Кристалл сурьменистого сернокислого натрия (Na5(SbO4(SO4)) имеет форму тетраэдра.

Правильные многогранники в химии Форму октаэдра имеет монокристалл алюмокалиевых квасцов (K(AL(SO4)2)*12H2O).

Правильные многогранники в химии Икосаэдр передает форму кристаллов бора В

Правильные многогранники в химии Кристалл пирита, или сернистый колчедан ( FeS ), – природная модель додекаэдра.

Правильные многогранники в физике Центры магнитных аномалий и магнитного поля планеты расположены в узлах системы треугольников икосаэдро-додекаэдровой структуры

Правильные многогранники в архитектуре бактерий и вирусов

Задачи для практической работы в группах Журналисты ( находят информацию о вирусах и бактериях в интернете ) Теоретики ( решают задачи о вирусах и бактериях) Практики ( делают модели правильных многогранников )

Бактерии и вирусы — это микроскопические организмы, которые могут вызывать заболевания, как у людей, так и у животных или растений. Хотя бактерии и вирусы могут иметь некоторые общие характеристики, они также очень разные. Бактерии обычно намного больше, чем вирусы, и их можно рассмотреть при помощи обычного микроскопа. Вирусы примерно в 1000 раз меньше бактерий и видны только под электронным микроскопом. Бактерии являются одноклеточными организмами, которые размножаются независимо от других организмов. Вирусы нуждаются в помощи живой клетки для воспроизведения.

Известно, что бактерии размножаются делением: одна бактерия делится на две; каждая из этих двух в свою очередь тоже делится на две , и получаются четыре бактерии ; из этих четырех в результате деления получаются восемь бактерий и т.д.(геометрическая прогрессия). Результат каждого удвоения будем называть поколением. Способность к размножению настолько велика, что если бы они не гибли от разных причин, а беспрерывно размножались, то за трое суток общая масса потомства одной только бактерии могла бы составить 7500 тонн. Как происходит размножение бактерий? Вернутся в материалы для групп Рефлексия

Задача №1 В благоприятных условиях бактерия размножается так, что за одну секунду делится на три. Сколько бактерий будет в пробирке через пять секунд? Ответ :121

Задача №2 Бактерия , попав в живой организм, к концу 20-й минуты делится на две бактерии, каждая из них к концу следующих 20 минут делится опять на две и т.д. Найдите число бактерий, образующихся их одной бактерии к концу суток.

Решение В сутках 1440 минут, каждые 20 минут появляется новое поколение- за 1 сутки 72 поколения. По формуле суммы n первых членов геометрической прогрессии, у которой b1=1 , q=2 , n=72 , находим, что S 72 = -1=4722366482869645213695= 4 ,7* бактерий в сутки от одной бактерии

Задача №3 Колония состояла из n бактерий. В неё попал вирус, который в первую минуту уничтожил одну бактерию, а затем разделился на два новых вируса. Одновременно каждая из оставшихся бактерий тоже разделилась на две новые. В следующую минуту возникшие два вируса уничтожили две бактерии, и затем оба вируса и все выжившие бактерии снова разделились, и так далее. Будет эта колония жить бесконечно долго или вымрет?

Решение Колония вымрет через n поколений. Предположим, что все бактерии исходной колонии были разных цветов, и все потомки бактерии какого-то цвета - того же цвета. Тогда вирус на первой минуте уничтожил, например, красную бактерию, вирусов стало 2, бактерий - 2(n-1), из них по 2 разных цветов. На второй минуте вирус уничтожил синих бактерий, все удвоилось, но на каждом шагу вирусов столько, сколько бактерий одного цвета. Т. о. , на каждой минуте становится на 1 цвет меньше, а всего цветов n, значит, столько минут колония и проживет . Вернутся в материалы для групп Рефлексия

Правильный тетраэдр Тетра́эдр — простейший многогранник, гранями которого являютсячетыре треугольника. У тетраэдра 4 грани, 4 вершины и 6 рёбер

Правильный октаэдр ОКТАЭДР— один из пяти выпуклых правильных многогранников, так называемых Платоновых тел. Октаэдр имеет 8 треугольных граней, 12 рёбер, 6 вершин, в каждой его вершине сходится 4 ребра.

Вирусы, патогенные для животных, отличаются кубический симметрией и представляют собой многогранники (тетраэдр, октаэдр, икосаэдр).

Октаэдр Результаты соединения нескольких тетраэдров

Правильный икосаэдр Пра́вильный икоса́эдр — правильный выпуклый многогранник , двадцатигранник , Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин — 12. Икосаэдр имеет 59 звёздчатых форм.

Головка вируса-бактериофага имеет форму икосаэдра

Бактериофаг Бактериофа́ги или фа́ги —вирусы , избирательно поражающие бактериальные клетки . Чаще всего бактериофаги размножаются внутри бактерий и вызывают их лизис

Вирус полиомиелита имеет форму додекаэдра.

Правильный додекаэдр Пра́вильный додека́эдр — один из пяти правильных многогранников. Додекаэдр составлен из двенадцати правильных пятиугольников, являющихся его гранями. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Таким образом, додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра).

Звездчатый икосаэдр Необычными являются астровирусы , имеющие звездчатую форму

Подведение итогов Домашнее задание: сделать модель многогранника и провести сопоставление изготовленной модели с природным аналогом

По теме: методические разработки, презентации и конспекты

План конспект , 2 презентации к уроку.

Кристаллы и правильные многогранники.

Методическое обоснование урока. Использование знаний из физики, астрономии, МХК, биологии на уроке геометрии при обобщении систематизации сведений по теме: «Симметрия в пространстве. Правил.

Всестороннее развитие геометрического мышления учащихся 6 классов с помощью методов геометрической наглядности, геометрическое конструирование, моделирование и дизайн.

Министерство общего и профессионального образования Свердловской области

Антонюк Елена Владимировна

Есть несколько причин, почему мы рассматриваем эту тему. Одной из них является та, что в практической деятельности и в быту мы постоянно встречаемся с предметами и объектами имеющими форму различных многогранников. Вы имеете представление о них, но только в узком смысле, и теперь выпал шанс изучить роль и значение этих пространственных тел. Вы узнаете о видах многогранников, истории их возникновения, я приведу примеры их применения и раскрою их значение в природе и практической деятельности человека.

Посмотрите вокруг — всюду геометрия! Геометрические знания и умения, геометрическая культура и развитие являются профессионально значимыми для многих современных специальностей, для дизайнеров и конструкторов, для рабочих и ученых.

Геометрия - это целый мир, который окружает нас с самого рождения.

Многогранники, несомненно, обладают красотой и используются в нашей жизни очень обширно.

• Пирамида - это многогранник, одна грань которого многоугольник, а остальные грани – треугольники с общей вершиной.

Правильные многогранники известны с древнейших времён. Их орнаментные модели можно найти на резных каменных шарах, созданных в период позднего неолита, в Шотландии, как минимум за 1000 лет до Платона. В костях, которыми люди играли на заре цивилизации, уже угадываются формы правильных многогранников.

Платон писал о них в своем трактате Тимей (360г до н. э.), где сопоставил каждую из четырёх стихий определённому правильному многограннику.

Евклид дал полное математическое описание правильных многогранников в последней, XIII книге Начал.

В XVI веке немецкий астроном Иоганн Кеплер пытался найти связь между пятью известными на тот момент планетами Солнечной системы (исключая Землю) и правильными многогранниками.

В модели Солнечной системы пять правильных многогранников помещались один в другой и разделялись серией вписанных и описанных сфер. Каждая из шести сфер соответствовала одной из планет. Многогранники были расположены в следующем порядке: октаэдр, за ним икосаэдр, додекаэдр, тетраэдр и, наконец, куб. Таким образом, структура Солнечной системы и отношения расстояний между планетами определялись правильными многогранниками.

Позже, от оригинальной идеи Кеплера пришлось отказаться, но результатом его поисков стало открытие двух законов орбитальной динамики — законов Кеплера, — изменивших курс физики и астрономии, а также правильных звёздчатых многогранников.

Это многогранники, у которых все многогранные углы равны, а грани - правильные, но разноимённые правильные многоугольники .

Многогранники такого типа открыл Архимед. Им подробно описаны 13 многогранников, которые позже были названы телами Архимеда.

Правильные звёздчатые многогранники

Их всего четыре, они называются также телами Кеплера-Пуансо .

Кеплер открыл малый додекаэдр, названный им колючим или ежом, и большой додекаэдр.

Пуансо открыл два других правильных звёздчатых многогранника, двойственных соответственно первым двум: большой звёздчатый додекаэдр и большой икосаэдр .

Правильные многогранники – самые выгодные фигуры, поэтому они широко распространены в природе.

Существует гипотеза, по которой ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете.

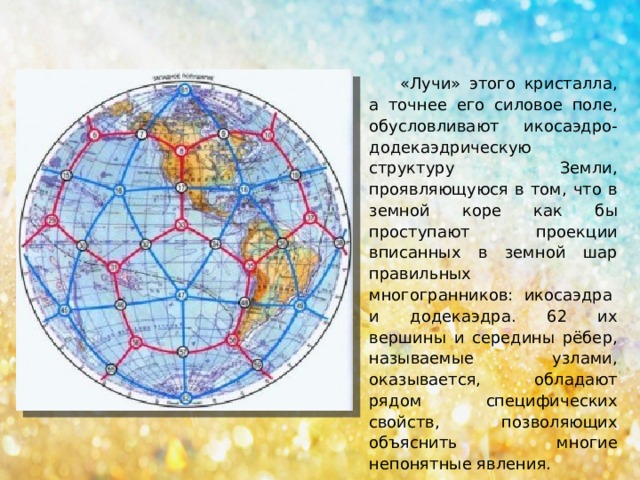
Ещё более удивительные вещи происходят в местах пересечения этих рёбер: тут располагаются очаги древнейших культур и цивилизаций: Перу, Северная Монголия, Гаити, Обская культура и другие. В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения Мирового океана, здесь шотландское озеро Лох-Несс, Бермудский треугольник.

МНОГОГРАННИКИ В БИОЛОГИИ, ГЕОЛОГИИ И ХИМИИ

В микро-мире многогранники встречаются в виде молекул, вирусов и бактерий - простейших организмов.

Скелет одноклеточного организма феодарии (Circjgjnia icosahtdra) по форме напоминает икосаэдр . Простейшее животное защищает себя двенадцатью иглами, выходящими из 12 вершин скелета. Оно больше похоже на звёздчатый многогранник.

Головка вируса-бактериофага также имеет форму икосаэдра .

Элементарной ячейкой воды являются тетраэдры , содержащие связанные между собой водородными связями пять молекул Н 2 О.

И из всего многообразия структур в природе базовой является гексагональная (шестигранная) структура , когда шесть молекул воды (тетраэдров) объединяются в кольцо. Такой тип структуры характерен для льда, снега и талой воды.

Кристаллическая решетка поваренной соли имеет кубическую структуру.

Многие горные породы имеют форму многогранников.

Кристаллы в форме октаэдра

Кристаллы в форме призм

МНОГОГРАННИКИ В МЕДИЦИНЕ

Призмы применяют в медицине, для лечения косоглазия. Принцип тренировки состоит в попеременном приставлении к тренируемым глазам на определенное время положительных сферо – призматических элементов различной сферической и призматической диоптрийности.

МНОГОГРАННИКИ В ФИЗИКЕ

В 60-х годах ХVII столетия Исаак Ньютон проводил эксперименты со светом. Чтобы разложить свет на составляющие и получить спектр, он использовал трёхгранную стеклянную призму.

Учёный обнаружил, что, собрав раздробленный луч с помощью второй призмы, можно опять получить белый свет. Так он доказал, что белый свет является смесью разных цветов. Проходя через призму, световые лучи преломляются. Ньютон первый разгадал, что солнечный луч многоцветный .

Оптика и электронные приборы

(очки, бинокли, объективы, телефоны)

МНОГОГРАННИКИ В ИСКУССТВЕ

Использовать многогранники в архитектуре люди стали очень давно, ещё до новой эры. И по мере роста строительного мастерства в мире появлялись новые шедевры, основанные на сложных геометрических фигурах.

Великая пирамида в Гизе является одним из 7 чудес древности и ярким примером многогранника. Кроме того, это единственное из чудес, сохранившееся до наших дней.

Александрийский маяк . Маяк состоял из трёх мраморных башен, стоявших на основании из массивных каменных блоков. Первая башня была прямоугольной , в ней находились комнаты, в которых жили рабочие и солдаты. Над этой башней располагалась меньшая, восьмиугольная башня со спиральным пандусом, ведущим в верхнюю башню. Верхняя башня формой напоминала цилиндр , в котором горел огонь, помогавший кораблям благополучно достигнуть бухты.

Многие готические соборы были построены с использованием расчётов, свойственных кубу.

Современная архитектура больших городов, ориентированная на возведение домов-коробок и однообразных конструкций, оказывает очень опасное влияние на человека.

Для корректировки зданий используется также и фэн шуй. Положения, объединённые под этим термином, представляют набор требований сакральной архитектуры и геометрии применительно к энергетическому моделированию жилого пространства. Применимость идей фэн шуй в строительстве помогает людям войти в резонанс с естественными человеческими и земными ритмами.

Шоколадная фабрика Nestle в Мексике. Стены представляют собой причудливый многогранник.

Роттердам - современный город с домами в 30, 40… и до 176 этажей. Практически все постройки представляют собой многогранники.

В эпоху Возрождения большой интерес к формам правильных многогранников проявили скульпторы, художники.

Сегодня вы узнали много интересного о применении многогранников, познакомились с историей их возникновения, ролью и значением в жизнедеятельности человека.

Живая природа.

Квазикристаллы Дана Шехтмана.

Как известно, плотное заполнение плоскости может быть осуществлено с помощью треугольников, квадратов и шестиугольников. С помощью пятиугольников (пентагонов) такое заполнение невозможно.

Таковы были каноны традиционной кристаллографии, которые существовали до открытия необычного сплава алюминия и марганца, названного квазикристаллом. Такой сплав образуется при сверхбыстром охлаждении расплава со скоростью 10 6 К в секунду. При этом при дифракционном исследовании такого сплава на экране упорядоченная картина, характерная для симметрии икосаэдра, обладающего знаменитыми запрещенными осями симметрии 5-го порядка.

Несколько научных групп во всем мире на протяжении нескольких последующих лет изучили этот необычный сплав посредством электронной микроскопии высокого разрешения. Все они подтвердили идеальную однородность вещества, в котором симметрия 5-го порядка сохранялась в макроскопических областях с размерами, близкими к размерам атомов (несколько десятков нанометров).

Тетраэдр в природе.

1. Фосфор

Более трехсот лет назад, когда гамбургский алхимик Геннинг Бранд открыл новый элемент - фосфор. Подобно другим алхимикам, Бранд пытался отыскать эликсир жизни или философский камень, с помощью которых старики молодеют, больные выздоравливают, а неблагородные металлы превращаются в золото. В ходе одного из опытов он выпарил мочу, смешал остаток с углем, песком и продолжил выпаривание. Вскоре в реторте образовалось вещество, светившееся в темноте. Кристаллы белого фосфора образованы молекулами Р₄. Такая молекула имеет вид тетраэдра.

2. Фосфорноватистая кислота Н₃РО_2.

Ее молекула имеет форму тетраэдра с атомом фосфора в центре, в вершинах тетраэдра находятся два атома водорода, атом кислорода и гидроксогруппа.

Кристаллическая решётка метана имеет форму тетраэдра. Метан горит бесцветным пламенем. С воздухом образует взрывоопасные смеси. Используется как топливо.

Молекула воды представляет собой маленький диполь, содержащий положительный и отрицательный заряды на полюсах. Так как масса и заряд ядра кислорода больше чем у ядер водорода, то электронное облако стягивается в сторону кислородного ядра. При этом ядра водорода “оголяются”. Таким образом, электронное облако имеет неоднородную плотность. Около ядер водорода имеется недостаток электронной плотности, а на противоположной стороне молекулы, около ядра кислорода, наблюдается избыток электронной плотности. Именно такая структура и определяет полярность молекулы воды. Если соединить прямыми линиями эпицентры положительных и отрицательных зарядов получится объемная геометрическая фигура - правильный тетраэдр.

Каждая молекула аммиака имеет не поделённую пару электронов у атома азота. Орбитали атомов азота, содержащие не поделённые пары электронов, перекрываются с sp 3 -гибридными орбиталями цинка(II), образуя тетраэдрический комплексный катион тетраамминцинка(II) [Zn(NH₃)₄] 2+ .

Элементарная ячейка кристалла алмаза представляет собой тетраэдр, в центре и четырех вершинах которого расположены атомы углерода. Атомы, расположенные в вершинах тетраэдра, образуют центр нового тетраэдра и, таким образом, также окружены каждый еще четырьмя атомами и т.д. Все атомы углерода в кристаллической решетке расположены на одинаковом расстоянии (154 пм) друг от друга.

Куб (гексаэдр) в природе.

Из курса физики известно, что вещества могут существовать в трёх агрегатных состояниях: твёрдом, жидком, газообразном. Они образуют кристаллические решётки.

Кристаллические решётки веществ - это упорядоченное расположение частиц (атомов, молекул, ионов) в строго определённых точках пространства. Точки размещения частиц называют узлами кристаллической решётки.

В зависимости от типа частиц, расположенных в узлах кристаллической решётки, и характера связи между ними различают 4 типа кристаллических решёток: ионные, атомные, молекулярные, металлические.

Ионными называют кристаллические решетки, в узлах которых находятся ионы. Их образуют вещества с ионной связью. Ионные кристаллические решётки имеют соли, некоторые оксиды и гидроксиды металлов. Рассмотрим строение кристалла поваренной соли, в узлах которого находятся ионы хлора и натрия. Связи между ионами в кристалле очень прочные и устойчивые. Поэтому вещества с ионной решёткой обладают высокой твёрдостью и прочностью, тугоплавки и нелетучи.

Форму куба имеют кристаллические решётки многих металлов (Li, Na, Cr, Pb, Al, Au, и другие).

Молекулярными называют кристаллические решётки, в узлах которых располагаются молекулы. Химические связи в них ковалентные, как полярные, так и неполярные. Связи в молекулах прочные, но между молекулами связи не прочные. Ниже представлена кристаллическая решётка I_2. Вещества с МКР имеют малую твёрдость, плавятся при низкой температуре, летучие, при обычных условиях находятся в газообразном или жидком состоянии. многогранник симметрия тетраэдр

Икосаэдр в природе.

Фуллерены - удивительные полициклические структуры сферической формы, состоящие из атомов углерода, связанных в шести - и пятичленные циклы. Это новая модификация углерода, для которой, в отличие от трех ранее известных модификаций (алмаза, графита и карбина), характерна не полимерная, а молекулярная структура, т.е. молекулы фуллеренов дискретны.

Свое название эти вещества получили по имени американского инженера и архитектора Ричарда Букминстера Фуллера, конструировавшего полусферические архитектурные сооружения, состоящие из шести- и пятиугольников.

Впервые фуллерены C₆₀ и C₇₀ были синтезированы в 1985 г Х. Крото и Р. Смолли из графита под действием мощного лазерного пучка. Получить C₆₀-фуллерен в количествах, достаточных для исследований, удалось в 1990 г Д. Хаффману и В. Кретчмеру, которые провели испарение графита с помощью электрической дуги в атмосфере гелия. В 1992 г. были обнаружены природные фуллерены в углеродном минерале - шугните (свое название этот минерал получил от названия поселка Шуньга в Карелии) и других докембрийских породах.

Молекулы фуллеренов могут содержать от 20 до 540 углеродных атомов, расположенных на сферической поверхности. Наиболее устойчивое и лучше изученное из этих соединений - C₆₀-фуллерен (60 атомов углерода) состоит из 20 шестичленных и 12 пятичленных циклов. Углеродный скелет молекулы C₆₀-фуллерена представляет собой усечённый икосаэдр.

В природе встречаются объекты, обладающие симметрией 5-го порядка. Известны, например, вирусы, содержащие кластеры в форме икосаэдра.

Строение аденовирусов также имеет форму икосаэдра. Аденовирусы (от греческого aden - железо и вирусы), семейство ДНК-содержащих вирусов, вызывающих у человека и животных аденовирусные болезни.

Вирус гепатита В - возбудитель гепатита В, основной представитель семейства гепадновирусов. Это семейство включает также гепатотропные вирусы гепатита сурков, сусликов, уток и белок. Вирус ГВ является ДНК-содержащим. Он представляет собой частицу диаметром 42-47 нм, состоит из ядра - нуклеоида, имеющего форму икосаэдра диаметром 28 нм, внутри которого находятся ДНК, концевой белок и фермент ДНК-полимераза.

Главная
• Список секций
• Математика
• Удивительный мир многогранников

Удивительный мир многогранников

Мое знакомство с многогранниками началось в пятом классе. На уроках мы учились строить изображения многогранников, определять количество вершин, граней и ребер, устанавливать соответствие между многогранником и его разверткой.

Цель исследования: познакомиться с видами многогранников, их применением в окружающем мире.

Объект исследования: многогранники.

Предмет исследования: многогранники и многогранные поверхности в окружающем мире.

- изучить исторический материал по данной теме;

- ознакомится с различными видами многогранников;

- рассмотреть область применения многогранников;

- изготовить модели многогранников.

Методы исследования: сбор информации, обработка данных, исследование, сравнение, анализ.

В течение многих веков математики проявляли живейший интерес к многогранникам. Интерес к ним обусловлен не только их красотой и оригинальностью, но и большой практической ценностью. Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне.

Многогранником называется поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело. Многоугольники, из которых составлен многогранник, называются его гранями. Стороны граней – рёбра многогранника, а концы рёбер – вершины многогранника.

Бывают выпуклыми и невыпуклыми. Выпуклый многогранник расположен по одну сторону от плоскости каждой своей грани. Невыпуклый многогранник расположен по разные стороны от плоскости одной из его граней.

Составлен из четырёх равносторонних треугольников.

Каждая его вершина является вершиной трёх треугольников.

Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырёх треугольников.

Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников.

Составлен из шести квадратов. Каждая вершина куба является вершиной трёх квадратов.

Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников.

Кроме полуправильных многогранников из правильных многогранников - можно получить так называемые правильные звездчатые многогранники. Это правильные невыпуклые многогранники, у которых грани пересекаются. Их всего четыре. Иоганн Кеплер (1571 – 1630 гг.) - немецкий математик, астроном, оптик, для которого правильные многогранники были любимым предметом изучения, впервые описал малый звездчатый

додекаэдр и большой звездчатый додекаэдр. А спустя 200 лет Луи Пуансо Пуансо (1777-1859) построил большой икосаэдр и большой додекаэдр.

Многогранники вокруг нас

Многогранники в искусстве

Исторически математика играла важную роль в изобразительном искусстве.

Леонардо да Винчи (1452 — 1519) увлекался теорией многогранников и часто изображал их на своих полотнах.

П равильные многогранники - имели особое очарование для голландского художник Морица Корнилиса Эшера (1898-1972). Во многих его работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов. На гравюре "Четыре тела" он изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.

Почтовые марки охватывают все значимые события в мире. Не обошли вниманием художники - филателисты и изображения многогранников. Почтовая марка, посвященная Леонарду Эйлеру с изображением икосаэдра, выпущена в 1983 г., в ГДР, к 200- летию ученого.

Н а выпущенной в 1980 году в Венгрии марке, изображен математик и астроном Иоганн Кеплер и его модель Вселенной на базе правильных многогранников.

Многогранники в архитектуре

И стория развития многогранников архитектуре уходит глубоко в историю. Многогранники начали использовать в архитектуре давно, более 7 тыс. лет. Великая пирамида в Гизе - эта грандиозная Египетская пирамида является древнейшим из семи чудес древности.

У Китая свои особенности использования многогранников в архитектуре. В основе лежит обязательно многогранник, который и служит основой для здания.

Многогранники не только придают прочность и устойчивость архитектурным сооружениям, но и красоту, изящество. Многие здания настолько красивы и сложны по своей форме, что требуют большого количества времени, сил. Современные архитекторы приобрели навык применения изящества, состоящие из множества сложных элементов, требующих большой работы.

П амятник правильным многогранникам в Германии

Стеклянная пирамида Лувра в Париже

З дание национальной библиотеки

Многогранники в химии и биологии

П равильные многогранники определяют форму кристаллических решеток некоторых химических веществ.Кристаллы многих металлов так же имеют форму куба (алюминий, серебро, свинец и др.)

Интересно, что именно икосаэдр оказался в центре внимания биологов. Чтобы установить форму вируса, брали различные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень – икосаэдр.

В ирус краснухи

Вирус ветряной оспы

Многогранники в природе

Правильные многогранники – самые выгодные фигуры, поэтому они широко распространены в природе.

Построенные пчелами соты представляют собой правильные шестиугольные призмы.

С древности люди пытались описать все возможные типы снежинок, составляли специальные атласы. Сейчас известно несколько тысяч различных типов снежинок. Снежинки - это звездчатые многогранники.

Мир кристаллов - мир не менее красивый и разнообразный. С кристаллами человечество познакомилось в глубокой древности. Связано это, в первую очередь, с их часто реализующейся в природе способностью самоограняться, т. е. самопроизвольно принимать форму изумительных по совершенству полиэдров. Даже современный человек, впервые столкнувшись с природными кристаллами, чаще всего не верит, что эти многогранники не являются делом рук искусного мастера.

Кристалл алмаза Кристалл рубина

Кристалл можно вырастить в домашних условиях.

Растворить соль в теплой воде. (Можно использовать поваренную соль (тогда кристалл будет прозрачный), но более красивый кристалл получается при использовании медного купороса (тогда кристалл будет синим). Можно использовать и другие вещества (сахар и различные соли)).

Когда соль перестанет растворяться в вашем растворе (получится перенасыщенный раствор), перелить его в другую емкость (лучше всего в прозрачную, так как тогда вы сможете легче наблюдать за ростом кристалла).

Постепенно наш кристалл будет расти и, когда он достигнет нужного размера, аккуратно вытащите его и обсушите.

Многогранники в географии

В географии – многогранники занимают важное место в исследовании залежей полезных ископаемых, которые тянутся вдоль икосаэдровододекаэдровой сетки.

Многогранники в жизни человека

С многогранниками мы знакомы с детских лет. О них напоминают окружающие нас предметы: кирпич, комната, книга, аквариум, различные упаковки и др.

В современном мире многие предметы интерьера имеют формы многогранников.

Многогранники очень декоративны, что позволяет широко применять их в ювелирной промышленности при изготовлении всевозможных украшений.

Многогранники и профессии

Плотник — профессия связана с механической обработкой дерева и превращением необработанной древесины в детали, конструкции и стройматериалы.

Слесарь — специалист по ручной (без использования станков) обработке металлов, включая операции по сборке и разборке на производстве или в быту.

Скульптор – это художник, занимающийся созданием скульптур, то есть произведений объемно-пространственной формы, трехмерных и осязаемых.

Практическим этапом моей работы стало изготовление моделей многогранников. Процесс изготовления моделей оказался очень увлекательным. Модели выполнены из разверток и в технике оригами.

Создание моделей правильных многогранников с помощью разверток

Чаще всего при создании моделей многогранников из плоских разверток используют такие развертки, в которых грани прилегают друг к другу ребрами, а модель строится путем загибания развертки вдоль ребер. Например, при создании моделей правильных многогранников чаще всего используют следующие развертки.

Создание моделей многогранников методами оригами

Сегодня оригами переживает очередную волну интереса. Появились новые направления оригами и области его применения. Так, математики открыли множество возможностей для решения геометрических и топологических задач. Архитекторы и строители увидели в оригамном конструировании возможности для создания многогранных структур из плоского листа. Из бумаги можно построить удивительные конструкции.

При написании исследовательской работы я изучила дополнительную литературу и расширила свои знания по данному вопросу: узнала, что многогранники имеют красивые формы, они обладают богатой историей, познакомилась с видами многогранников. Решая поставленную проблему, я убедилась, что многогранники – это не просто геометрические тела , они окружают нас в жизни, в природе, в искусстве, архитектуре, науке. Многогранник – это величайшее открытие человечества. Систематизировав полученную информацию, я заметила, что в окружающем мире преобладают правильные многогранники.

Практическим этапом моей работы стало изготовление моделей многогранников. Процесс изготовления моделей оказался очень увлекательным. Модели выполнены из разверток и в технике оригами.

Цель моей работы достигнута.

Список литературы и Интернет – ресурсов

Бунимович Е.А.Математика 6. – М.: Просвещение, 2016

Ворошилов А.В. Математика и искусство. - М.: Просвещение, 1992

Шарыгин И. Ф., Ерганжиева Л.Н. Наглядная геометрия. Учебное пособие для V – VI классов. – М: Мирос 1992.

Энциклопедия для детей. Я познаю мир. Математика. – М: Издательство АСТ, 1999