Сообщение по математике про прогрессию в вирусах

Главная
• Список секций
• Математика
• Применение понятия "прогрессия" в жизни

Применение понятия "прогрессия" в жизни

1. Выяснить, имеют ли прогрессии практическое применение в повседневной жизни.

1. Арифметическая и геометрическая прогрессии.

1. Практическое применение прогрессий в жизни.

(см. Приложение 1)

Результаты анкетирования оказались неоднозначными. Всего было опрошено 35 человек, из них 31 % ответили на вопрос положительно, а 69 % не знают, как применять свойства прогрессии в жизни.

Также мы провели еще одно анкетирование и выяснили, что большая часть опрошенных (83 %) хотела бы узнать о необычном применении прогрессии в жизни. В связи с этим, мы считаем, что данная тема является интересной для изучения на сегодняшний день.

Определения и формулы

- это числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с постоянным для этой последовательности числом d.

Число d называется разностью прогрессии.

Любой член арифметической прогрессии вычисляется по формуле:

Сумма n первых членов арифметической прогрессии вычисляется по формуле:

- это числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на постоянное для этой последовательности число q.

Число q называется знаменателем прогрессии.

Любой член геометрической прогрессии вычисляется по формуле:

Сумма n первых членов геометрической прогрессии вычисляется по формуле:

Зная эти формулы можно решить большое количество интересных задач: литературного, исторического и практического содержания.

Первые представления об арифметической и геометрической прогрессиях были еще у древних народов. Задачи на прогрессии, дошедшие до нас из древности, были связаны с запросами хозяйственной жизни: распределение продуктов, деление наследства и др.

На связь между прогрессиями первым обратил внимание великий ученый Архимед (287–212 гг. до н. э). Для нахождения площадей и объемов фигур он вывел формулу суммы квадратов натуральных чисел.

Термин “прогрессия” (от латинского progression , что означает движение вверх) был введен римским автором Боэцием (в VI веке) и понимался в более широком смысле, как бесконечная числовая последовательность.

Формула суммы членов арифметической прогрессии была доказана древнегреческим ученым Диофантом (в 3 веке).

Формула суммы членов геометрической прогрессии дана в книге Евклида “Начала” (3 век до н.э.).

Сведения, связанные с прогрессиями, впервые встречаются в дошедших до нас документах Древней Греции. Уже в V в. до н. э. греки знали следующие прогрессии и их суммы:

Известна интересная история о знаменитом немецком математике К. Гауссе (1777 – 1855), который еще в детстве проявлял выдающиеся способности к математике. Учитель предложил учащимся сложить все натуральные числа от 1 до 100. Маленький Гаусс решил эту задачу за одну минуту, сообразив, что суммы 1+100, 2+99 и т.д равны, он умножил 101 на 50, т.е. на число таких сумм. Иначе говоря, он заметил закономерность, присущую арифметическим прогрессиям.

Шахматная игра была придумана в Индии, и когда индусский царь Шерам познакомился с нею, он был восхищен её остроумием и разнообразием возможных в ней положений. Узнав, что она изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку. Изобретатель, его звали Сета, явился к трону повелителя. Это был скромно одетый ученый, получавший средства к жизни от своих учеников.

Изобретатель шахмат попросил в награду за свое изобретение столько пшеничных зерен, сколько их получится, если на первую клетку шахматной доски положить одно зерно, на вторую – в 2 раза больше, т. е. два зерна, на третью – еще в 2 раза больше, т. е. 4 зерна и так далее до 64 – ой клетки.

Царь был удивлен, когда узнал, что такую, казалось бы, скромную просьбу невозможно выполнить.

Можно подсчитать, что масса такого числа пшеничных зерен больше триллиона тонн. Это заведомо превосходит количество пшеницы, собранной человечеством до настоящего времени.

Если бы царю удалось засеять пшеницей площадь всей поверхности Земли, считая моря, и океаны, и горы, и пустыню, и Арктику с Антарктикой, и получить удовлетворительный урожай, то, пожалуй, лет за 5 он смог бы рассчитаться.

Применение прогрессий в жизни

1. Финансовая пирамида.

Разберёмся в механизмах этих организаций.

Финансовая пирамида – способ обеспечения дохода участникам структуры за счет постоянного привлечения денежных средств. Доход первым участникам пирамиды выплачивается за счет вкладов последующих участников. В большинстве случаев истинный источник получения дохода скрывается, а декларируется вымышленный или малозначимый. Подобная подмена является мошенничеством.

Как правило, в финансовой пирамиде обещается высокая доходность, которую невозможно поддерживать длительное время, а погашение обязательств пирамиды перед всеми участниками является заведомо невыполнимым. Закономерным итогом такой ситуации является банкротство проекта и убытки последних инвесторов.

Человек собирается организовать финансовую пирамиду.

Представим, что число участников увеличивается в 5 раз с каждым кругом. В первом кругу участвуют 120 человек, во втором – 600, в третьем – 3 000, на четвертом – 15 000, на пятом – 75 000, на шестом – 375 000, на седьмом – 1 875 000, на восьмом – 9 375 000, на девятом – 46 875 000, на десятом – 234 375 000 человек.

Численность населения Воронежа составляет 1 039 801 человек (данные 2018 года). Следовательно, на седьмом кругу количество участников финансовой пирамиды превысит численность населения нашего города.

Численность населения России составляет 146 877 088 человек (данные 2018 года). Можно заметить, что на десятом кругу количество участников значительно превышает численность населения страны.

Так что участник, включившийся на седьмом или десятом круге, уже ничего не получит.

Такая закономерность чисел, также является геометрической прогрессией

В жизненной практике геометрическая прогрессия появляется в первую очередь в задаче об исчислении так называемых “сложных процентов”.

Каждому в жизни приходится решать задачи, связанные с денежными вкладами.

Применение понятия на практике

Воспользуемся конкретным примером. Размер материнского капитала составляет 453 000 р. Можно ли вложить такую сумму в банк под выгодный процент и к совершеннолетию ребенка приобрести ему квартиру?

Первоначально вложено 453 000 р. через год сумма возрастет на 5% составит 105% от 453 000 р.

453 000 * 1, 05 (сумма составит через год)

453 000; 453 000 * 1, 05; 453 000 * 1, 05 2 ; 453 000 * 1, 05 3 ; 453 000 * 1, 05 4

Последовательность имеет вид геометрической прогрессии, где

b ₁ = 453 000; g = 1, 05

453 000 * 1, 05 18 = 1, 0902 * 10 6 = 1090200 р.

Учитывая, что средняя стоимость однокомнатной квартиры в г. Воронеже составляет 1900000 р., на сумму 1090200 приобрести жилище не возможно, но подобное вложение денежных средств является достаточно выгодным.

В XIII веке в Англии ростовщики давали деньги под 50% годовых. Это вызывало страшное недовольство. Издавались законы, ограничивающие процент. Король Генрих VII даже совсем отменил взимание процентов, что привело в упадок, как банковское дело, так и промышленность, лишившуюся возможности получения кредитов. В конце концов, взимание процентов было разрешено, но не должно было быть большим 10%.

3. Изменение массы радиоактивного вещества со временем - еще один пример геометрической прогрессии.

Известно, что за единицу времени такое вещество теряет определенную часть своей массы (она переходит в другое вещество и энергию). Для каждого радиоактивного вещества определяется величина T –период полураспада. Массы нераспавшегося вещества в моменты 0, T, 2T, 3T,… будут образовывать бесконечно убывающую геометрическую прогрессию.

4. Прирост древесины в лесном массиве происходит по законам геометрической прогрессии. При этом у каждой породы дерева свой коэффициент годового роста объема. Учет этих изменений позволяет планировать вырубку части лесных массивов и одновременную работу по восстановлению лесов.

5. Прогрессии в природе

Все организмы обладают интенсивностью размножения в геометрической прогрессии.

Известно, что бактерии размножаются делением: одна бактерия делится на две; каждая из этих двух в свою очередь тоже делится на две, и получаются четыре бактерии; из этих четырех в результате деления получаются восемь бактерий и т. д. (геометрическая прогрессия). Результат каждого удвоения называется поколением.

Способность к размножению у бактерий настолько велика, что если бы они не гибли от разных причин, а беспрерывно размножались, то за трое суток общая масса потомства одной только бактерии могла бы составить 7500 тонн. Таким громадным количеством бактерий можно было бы заполнить около 375 железнодорожных вагонов.

Интенсивность размножения бактерий использую в пищевой промышленности (для приготовления напитков, кисломолочных продуктов, при квашении, солении и др.), в фармацевтической промышленности (для создания лекарств, вакцин), в сельском хозяйстве (для приготовления силоса, корма для животных), в коммунальном хозяйстве и природоохранных мероприятиях (для очистки сточных вод, ликвидации нефтяных пятен).

6. Прогрессии - оправдание войн

Английский экономист епископ Мальтус использовал геометрическую и арифметическую прогрессии для оправдания войн: средства потребления (пища, одежда) растут по законам арифметической прогрессии, а люди размножаются по законам геометрической прогрессии. Мальтус считал, для того, чтобы избавиться от лишнего населения, необходимы войны.

Человек получил наследство. Первый месяц он истратил 100$, а каждый следующий месяц он тратил на 50$ больше, чем в предыдущий. Каков размер наследства, если денег хватило на год такой безбедной жизни?

9. Прогрессии в музыке

В музыке прогрессией называется постепенное повторение мотива в один или два такта в восходящем или нисходящем порядке. При таком повторении мотива выбирается интервал, на который мотив должен постоянно перестанавливаться в восходящем или нисходящем направлении. Прогрессия бывает точная или неточная. В точной, мотив повторяется на другой ступени буквально, т. е. с сохранением не только названий всех своих интервалов, но и их точной величины. В неточной прогрессии допускаются отступления от точной величины интервалов мотива, и интервала, на которой мотив перестанавливается. Прогрессия в музыке называется секвенцией.

10. Прогрессии в литературе

Даже в литературе мы встречаемся с математическими понятиями. Вспомним строки из "Евгения Онегина".

. Не мог он ямба от хорея,

Как мы не бились отличить.

Ямб - это стихотворный размер с ударением на чётных слогах 2; 4; 6; 8. Номера ударных слогов образуют арифметическую прогрессию с первым членом 2 и разностью прогрессии 2.

Прогрессия: 2; 4; 6; 8.

Хорей - это стихотворный размер с ударением на нечётных слогах стиха. Номера ударных слогов образуют арифметическую прогрессию 1; 3; 5; 7. С первым членом 1 и разностью прогрессии 2.

Прогрессия: 1; 3 ;5; 7.

Как вы могли заметить, исходя из вышеизложенного материала, что зная основные формулы геометрической и арифметической прогрессий, можно решить большое количество интересных задач литературного, исторического и практического содержания. Формулы и математические законы описывают явления в разных областях знаний, на первый взгляд далеких от математики.

На сегодняшний день, изучение происхождения и использования в жизни геометрической и арифметической прогрессий является актуальной и важной задачей для современных ученых.

Дэвисон Р. К. Прогрессии / Р. К. Дэвисон. - М. Мир Урании 2016г. 328 стр.

Рассел Д. Геометрическая прогрессия / Д. Рассел. - Издательство: "VSD" (2012)

Рассел Д. Арифметическая прогрессия / Д. Рассел. - Издательство: VSD, 2012 г.

Анкета для учащихся 10 - го класса.

Ответ на поставленный

Знаете ли Вы как применить свойства прогрессии в повседневной жизни?

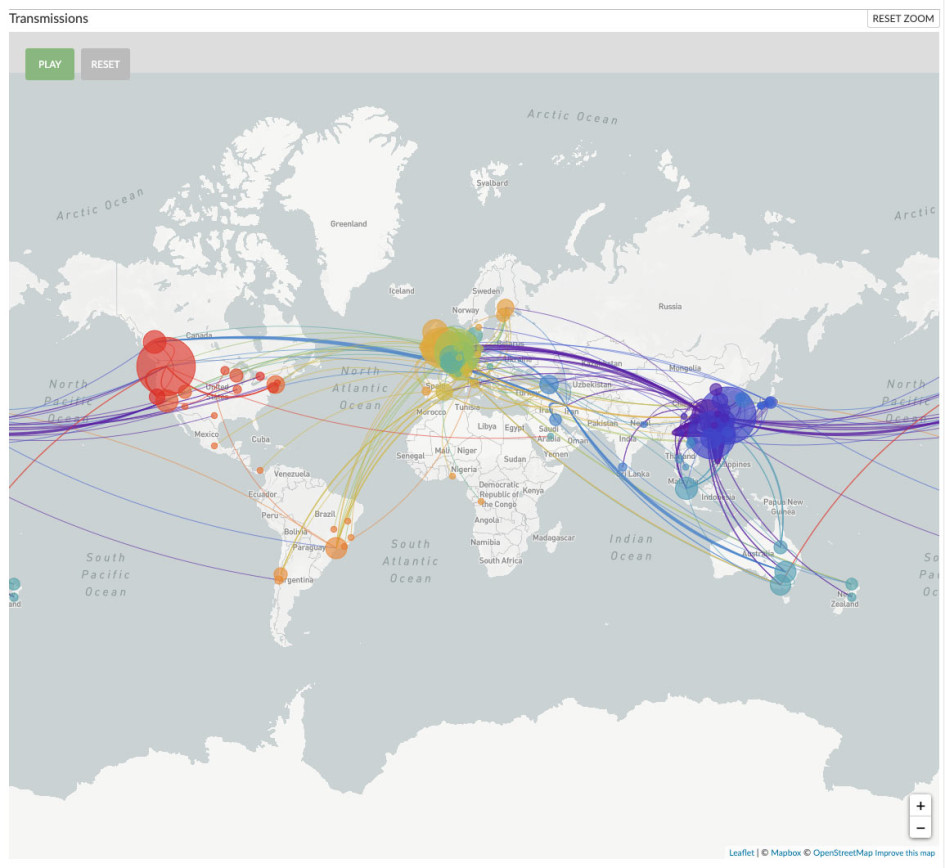
Детектив: откуда взялся COVID-19 и как перемещается (ENG)

Демография имеет значение (ENG)

Поскольку летальность COVID-19 значительно увеличивается с возрастом пациента, особенности возрастных структур населения могут оказывать значительный эффект на общую смертность от пандемии коронавируса. Демограф Илья Кашницкий оценил этот эффект и отобразил на карте различия в возрастных структурах населения регионов Европы.

За основу взяли данные о летальности пандемии в Италии — первой европейской стране, где ситуация начала развиваться очень быстро, и к 17 марта было зафиксировано уже 2003 смерти. Предположив, что во всех прочих регионах Европы летальность будет такой же как мы наблюдали в Италии, а общее число инфицированных достигнет 2/3 населения (цифра, о которой упоминала в своем обращении Ангела Меркель), рассчитали долю населения с повышенным риском умереть от пандемии. Надо отметить, что эта величина не претендует на роль сколько-нибудь точного прогноза финальной летальности. Допущения при расчетах очень значительны и маловероятны в долгосрочной перспективе. Однако, суть исследования — в сравнении возрастных структур населения. Различия между ними останутся неизменными, даже если повозрастная летальность от COVID-19 окажется существенно отличной от наблюдаемых сейчас в Италии величин, важно лишь, чтобы различия между возрастными группами оставались схожими.

Проведенный анализ позволяет выявить потенциально наиболее уязвимые регионы. Наибольшие потери населения из-за пандемии вероятны в странах и регионах с наиболее возрастным населением — Италия, Германия и Испания. Самый интересный вывод: несмотря на то, что сейчас наибольшее количество зарегистрированных случаев заражения и смертей концентрируется в больших городах, куда вирус пришел раньше, при масштабном неконтролируемом распространении наиболее проблемными станут отдаленные периферийные районы с наиболее пожилым населением. Это еще одна причина, почему карантинные меры, призванные растянуть во времени пик пандемии, чрезвычайно важны, особенно в странах Европы с относительно старым населением.

Источник: Kashnitsky, I. (2020). COVID-19 in unequally ageing European regions. OSF Preprint.

Экспоненциальный рост и эпидемии (ENG, RUS)

Математик объясняет, в какой момент нужно начинать беспокоиться. Эпидемия развивается экспоненциально — это значит умножение на какую-то константу (постоянный коэффициент).

Согласно данным на начало марта число случаев каждый день превышало число случаев в предыдущий день в 1,12—1,25 раз. Изменение количества зараженных изо дня в день складывается из трех цифр: количество зараженных в определенный день (N), среднее количество человек, с которым зараженный может контактировать в определенный день (E), и вероятность каждого контакта стать новым случаем заражения (p). Соответственно, по данным на 6 марта, в среднем каждые 16 дней количество зараженных увеличивалось в 10 раз. Но просто провести восходящий тренд недостаточно: в какой момент рост кривой должен остановиться. И важную роль начинают играть переменные E и p — они должны снижаться, чтобы остановить экспоненциальный рост.

Интерактивная модель: как распространяется вирус (ENG)

У The Washington Post вышел интерактивный материал о том, как распространяются инфекции. Основная идея — показать, почему важно ограничивать контакты каждого конкретного человека с внешним миром, а вот закрывать города и страны совсем необязательно. Симуляции показывают, как изменяется кривая количества зараженных в зависимости от того, какая стратегия используется: не делать ничего; попытка закрыть город на карантин; социальная изоляция четверти населения; социальная изоляция 7/8 населения.

Мягкая изоляция выигрывает у карантина, а почти полная изоляция — статистически наиболее надежный способ остановить эпидемию. Симуляции случайные, каждое прочтение статьи даст немного разные результаты, но вывод останется прежним.

Блогер Кевин Симлер улучшил эту модель: он добавил новые вводные (например, инкубационный период и количество умерших от болезни) и параметры модели, которые можно настраивать вручную. Здесь по шагам объясняется, как распространяется вирус и какие переменные на это влияют: например, в одной из симуляций предлагается угадать, какой должна быть скорость передачи заболевания между людьми, чтобы она не успела заразить все население планеты.

Так что это не только подробное пошаговое объяснение того, как распространяется вирус, но еще и упражнение в интуиции и критическом мышлении.

Люди хотят закрытия границ (RUS)

По данным исследования Ipsos по восприятию коронавируса, большинство людей считают, что границы их стран должны быть закрыты до тех пор, пока не будет локализована эпидемия. В опросе приняли участие 12 000 человек из 12 стран. Жители Азиатско-Тихоокеанского региона активнее всех поддерживают идею закрытия границ — во главе с Индией (79%) и Вьетнамом (78%) — что неудивительно, учитывая локацию, в которой болезнь была обнаружена впервые. В Италии 76% также согласны с этой радикальной мерой. Далее следуют Китай (73%) и Россия (70%).

Растет количество человек, которые верят в вероятность заражения людей из их ближнего окружения: их уже больше половины респондентов во Вьетнаме (67%), Великобритании (57%), половина в Индии, Австралии и Японии (51%).

Что ученые знают о 2019-nCoV (RUS)

Сейчас идет разработка лекарств, которые ингибируют заражение на разных стадиях цикла репликации вируса, и вакцин от SARS-CoV/MERS-CoV. Однако пока специфических препаратов от коронавирусов нет, и лечение заключается в поддерживающей терапии, назначенной по состоянию пациента. Источник на 11 марта 2020 года.

Материал обновляется.

Описание презентации по отдельным слайдам:

Действительно ли прогрессии играют большую роль в нашей жизни?

Прогрессии имеют определенное практическое значение.

Установить картину возникновения понятия прогрессии и выявить примеры их применения.

1 Изучить наличие задач на прогрессии с практическим содержанием . 2. Выяснить: - когда и в связи с какими потребностями человека появилось понятие последовательности, в частности -прогрессии; - какие ученые внесли большой вклад в развитие теоретических и практических знаний по изучаемой проблеме. 3. Установить: имеют ли арифметическая и геометрическая прогрессии прикладное значение? Найти примеры применения прогрессий в нашей жизни.

Объект исследования: последовательности: арифметическая и геометрическая прогрессии. Предмет исследования: практическое применение этих прогрессий Основная идея исследования: Показать, как на протяжении многих веков формировалось представление о прогрессиях

Изучить историю возникновения прогрессий Познакомиться с древнейшей арифметической прогрессией Прогрессия на клетчатой бумаге Старинная задача и геометрическая прогрессия. Применение прогрессий в разных отраслях Оформить презентацию

Понятие числовой последовательности возникло и развивалось задолго до создания учения о функциях. На связь между прогрессиями первым обратил внимание великий АРХИМЕД (ок. 287–212 гг. до н.э)

Термин “прогрессия” был введен римским автором Боэцием еще в IV в. н.э. От латинского слова progressio – “движение вперед” и понимался в более широком смысле, как бесконечная числовая последовательность. Названия “арифметическая” и “геометрическая” были перенесены из теории непрерывных пропорций, которыми занимались древние греки. Примеры отдельных арифметических и геометрических прогрессий можно встретить еще в древневавилонских и греческих надписях, имеющих возраст около четырех тысячелетий и более

Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом. Это число называется разностью арифметической прогрессии. Каждая арифметическая прогрессия имеет вид: a, a + d, a + 2d, a + 3d, . Формула суммы членов арифметической прогрессии была доказана древнегреческим ученым Диофантом (в 3 веке).

Числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предшествующему члену, умноженному на одно и то же не равное нулю число, называется геометрической прогрессией.

Формула суммы членов геометрической прогрессии дана в книге Евклида “Начала” (3 век до н.э.). Для нахождения суммы числа членов геометрической прогрессии применяют следующую формулу:

Древнейшая задача: Сто мер хлеба разделить между пятью людьми так, чтобы второй получил настолько же больше первого, насколько третий получил больше второго, четвертый больше третьего и пятый больше четвертого. Кроме того, двое первых должны получить в 7 раз меньше трех остальных. Сколько нужно дать каждому?

Очевидно, количества хлеба, полученные участниками раздела, составляют возрастающую арифметическую прогрессию. Пусть первый её член x, разность у. Доля первого X Доля второго X+Y Доля третьего X+2Y Доля четвертого X+3Y Доля пятого X+4Y

На основании условий задачи составляем систему двух уравнений: После упрощения получим: Решив эту систему, получим

Значит хлеб должен быть распределен на следующие части: люди Полученная доля первый второй третий четвертый пятый

Формулу суммы членов арифметической прогрессии легко вывести простым и наглядным приемом с помощью клетчатой бумаги. На такой бумаге любая арифметическая прогрессия изображается ступенчатой фигурой. Например, прогрессия 2;5; 8; 11; 14… имеет вид:

B A C E G Дополним ступенчатую фигуру до прямоугольника. Получим прямоугольник, состоящий из двух равных фигур, площадь каждой из них изображает сумму членов нашей прогрессии. Значит, двойная сумма нашей прогрессии равна площади прямоугольника ABGE, т.е. Hо изображает сумму 1-го и 5-го членов прогрессии; - число членов прогрессии. Поэтому двойная сумма или D 5 2 4 3 3 4 2 5 1

Рассуждая об арифметической и геометрической прогрессиях, хочется лишний раз повторить, что за видимой простатой прогрессии скрывается большой прикладной потенциал. Для решения некоторых задач по физике, геометрии, биологии, химии, экономике, строительному делу пользуются знаниями арифметической и геометрической прогрессии.

При повышении температуры по арифметической прогрессии скорость химических реакций растёт по геометрической прогрессии.

Вписанные друг в друга правильные треугольники образуют геометрическую прогрессию.

Нейтрон, ударяя по ядру урана, раскалывает его на две части. Получаются 2 нейтрона. Затем два нейтрона, ударяя по двум ядрам, раскалывает их ещё на 4части и т.д. - это геометрическая прогрессия Равноускоренное движение — арифметическая прогрессия, т.к. за каждые промежутки времени тело увеличивает скорость в одинаковое число раз.

Микроорганизмы размножаются делением пополам, поэтому при благоприятных условиях, через одинаковый промежуток времени их число удваивается.

Вклады в банках увеличиваются по схемам сложных и простых процентов. Простые проценты – увеличение первоначального вклада в арифметической прогрессии, сложные проценты – увеличение в геометрической прогрессии

Возведение многоэтажного здания — пример арифметической прогрессии. Каждый раз высота здания увеличивается на 3 метра.

Даже деревенские слухи можно описать с помощью геометрической прогрессии. Приведем пример. В поселке 2 000 жителей. Приезжий рассказывает новость трем соседям; каждый из них рассказывает новость уже трем своим соседям и т. д. Новость распространяются с геометрической прогрессией.

В ходе работы было установлено, что сами по себе прогрессии известны так давно, что нельзя говорить о том, кто их открыл. Также я убедились в том, что задачи на прогрессии, дошедшие до нас из древности, также как и многие другие знания по математике, были связаны с запросами хозяйственной жизни. Я выяснила, какие ученые внесли свой вклад в развитие теории прогрессий и как теоретические знания применяются на практике в современной жизни.

Сделав анализ задач, я увидела, что прогрессии встречаются при решении задач в химии, в строительстве, в банковских расчетах, в физике , в биологии , в геометрии и в других жизненных ситуациях. На основе полученных данных можно сделать вывод о том, что знания арифметической и геометрической прогрессий помогают человечеству решать многие проблемы. Арифметическая и геометрическая прогрессии не только связаны с красивыми задачами и легендами прошлого, но и позволяют изучать часто встречающиеся на практике процессы. Таким образом, выдвинутая мною гипотеза подтверждена.

Выберите книгу со скидкой:

ОГЭ. География. Новый полный справочник для подготовки к ОГЭ

350 руб. 242.00 руб.

География. Для тех, кто хочет все успеть

350 руб. 154.00 руб.

Современная школа игры на фортепиано

350 руб. 410.00 руб.

Готовимся к школе. Учимся проходить лабиринты.KUMON

350 руб. 541.00 руб.

Математика. Новый полный справочник школьника для подготовки к ЕГЭ

350 руб. 222.00 руб.

Дошкольная педагогика с основами методик воспитания и обучения. Учебник для вузов. Стандарт третьего поколения. 2-е изд.

350 руб. 963.00 руб.

Краткий справочник по биологии

350 руб. 162.00 руб.

Рисую узоры: для детей 4-5 лет. Ч. 2

350 руб. 145.00 руб.

Все словарные слова. 3 класс

350 руб. 121.00 руб.

Английский язык: для детей 5-6 лет. Ч. 1. 2-е изд., испр. и перераб.

350 руб. 145.00 руб.

Считаю и решаю: для детей 5-6 лет. Ч. 1, 2-е изд., испр. и перераб.

350 руб. 145.00 руб.

Прописи. Комплект из 3-х частей

350 руб. 195.00 руб.

БОЛЕЕ 58 000 КНИГ И ШИРОКИЙ ВЫБОР КАНЦТОВАРОВ! ИНФОЛАВКА

В настоящее время актуальным вопросом становится проблема соотношения, изучаемого в школьном курсе математики, материла с жизнью

Изучая данную тему, необходимо заинтересовать обучающихся, имеет ли это, какое - либо практическое значение и как давно люди знают последовательности, как возникло это понятие. Перед учащимися ставится вопрос: в каких жизненных ситуациях можно применить знания о прогрессиях?

• Черемисина Татьяна ВасильевнаНаписать 0 13.04.2018

Номер материала: ДБ-1444512

Добавляйте авторские материалы и получите призы от Инфоурок

Еженедельный призовой фонд 100 000 Р

Спикер: Анна Быкова (#лениваямама)

06.04.2018 323

06.04.2018 489

27.03.2018 362

16.03.2018 204

09.03.2018 297

28.02.2018 435

24.02.2018 1427

11.02.2018 720

Не нашли то что искали?

Вам будут интересны эти курсы: