Вирус в форме икосаэдра

(от греческого ico – двадцать и hedra – грань)

Правильный выпуклый многогранник, составленный из 20 правильных треугольников. Каждая из 12 вершин икосаэдра является вершиной 5 равносторонних треугольников, поэтому сумма углов при вершине равна 300 ° .

У икосаэдра 30 ребер. Как и у всех правильных многогранников ребра икосаэдра имеют равную длину, а грани - равную площадь. Обозначим длину ребра икосаэдра а и получим следующие формулы:

Икосаэдр имеет 15 осей симметрии, каждая из которых проходит через середины противоположных параллельных ребер. Точка пересечения всех осей симметрии икосаэдра является его центром симметрии.

Плоскостей симметрии также 15. Плоскости симметрии проходят через четыре вершины, лежащие в одной плоскости, и середины противолежащих параллельных ребер.

Природа говорит языком математики; буквы этого языка -
круги, треугольники и другие математические фигуры.
Галилео Галилей

В природе встречаются объекты, обладающие симметрией 5-го порядка. Известны, например, вирусы, содержащие кластеры в форме икосаэдра. Открытие фуллерена, молекула которого С₆₀ также обладает этим типом симметрии, стимулировало интерес к подобным объектам. Г.Хуберт с сотрудниками (H.Hubert ; Аризонский университет, США) синтезировали кристаллы B₆O из смеси B и B₂O₃, которая выдерживалась при температуре 1700 o С и давлении от 4 до 5.5 ГПа в течение 30 мин. Образовавшийся субоксид бора имеет ромбоэдрическую кристаллическую решетку с одним из плоских углов при вершине, равным 63.1 o . Это значение очень близко к величине угла 63.4 o , необходимого для того, чтобы из 20 тетраэдров можно было составить правильный икосаэдр.
Первичные икосаэдры способны группироваться в более крупные кластеры: центральный икосаэдр окружен 12 такими же частицами, центры которых лежат в вершинах более крупного икосаэдра второго порядка. Число атомов в таком сверхкластере может достигать 10 14 . Икосаэдричесий кластер имеет размер около 15 мкм. Этот продукт синтеза не может считаться монокристаллом, так как не имеет периодической кристаллической решетки. Малая плотность таких частиц при твердости, близкой к твердости алмаза, и высокая химическая стойкость делают их перспективными в создании новых материалов для техники.

Исключительностью икосаэдра среди Платоновых тел воспользовались вирусы. По-видимому, тут все дело в экономии — экономии генетической информации.Вы можете спросить: а почему обязательно правильный многогранник? И почему именно икосаэдр?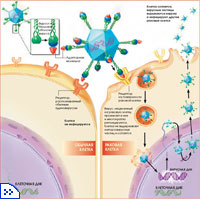
Вирусная частица должна весь обмен клетки-хозяина перевернуть вверх дном; она должна заставить зараженную клетку синтезировать многочисленные ферменты и другие молекулы, необходимые для синтеза новых вирусных частиц. Все эти ферменты должны быть закодированы в вирусной нуклеиновой кислоте. Но количество ее ограничено. Поэтому для кодирования белков собственной оболочки в нуклеиновой кислоте вируса оставлено совсем мало места. Что же делает вирус? Он просто использует много раз один и тот же участок нуклеиновой кислоты для синтеза большого числа стандартных молекул — строительных белков, объединяющихся в процессе автосборки вирусной частицы. В результате достигается максимальная экономия генетической информации. Остается добавить, что по законам математики для построения наиболее экономичным способом замкнутой оболочки из одинаковых элементов нужно сложить из них икосаэдр, который мы наблюдаем у вирусов.

Строение аденовирусов также имеет форму икосаэдра. Аденовирусы (от греческого aden - железо и вирусы), семейство ДНК-содержащих вирусов, вызывающих у человека и животных аденовирусные болезни.

Вирус кошачьей панлейкопении (FPLV) принадлежит к семейству парновирусов. Родственных возбудителей среди распространенных болезней человека нет. Вирус - сферический двадцатигранник - икосаэдр, мелкий, размер около 20 нм (0,00002 мм), простой по структуре, не имеет внешней оболочки; геном одна молекула однотяжевой ДНК с молекулярной массой около 2 млн. Вирус очень стабилен, может сохранять активность вне организма месяцы и годы.

Икосаэдр в природе

Фуллерены

Молекула фуллерена С 60 - усеченный икосаэдр с атомами углерода в вершинах. Он имеет 32 грани (12 пятиугольных и 20 шестиугольных), 60 вершин и 90 ребер (60 на границе пяти- и шестиугольников и 30 на границе только шестиугольников). Направляющие ребра такого многогранника образуют некоторое подобие мозаики Пенроуза.

В этой молекуле, напоминающей покрышку футбольного мяча и имеющую структуру правильного усеченного икосаэдра, атомы углерода располагаются на сферической поверхности в вершинах 20 правильных шестиугольников и 12 правильных пятиугольников так, что каждый шестиугольник граничит с тремя шестиугольниками и тремя пятиугольниками, а каждый пятиугольник граничит с шестиугольниками.

Скелет одноклеточного организма феодарии ( Circogonia icosahedra ) по форме напоминает икосаэдр.

Скорее всего, такая природная геометризация феодарий вызвана уникальной формой этого многогранника (напоминаем, что он имеет наибольший объём при наименьшей площади), помогающей морскому организму преодолевать давление водной толщи: большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное защищает себя двенадцатью иглами, выходящими из 12 вершин скелета. Он больше похоже на звёздчатый многогранник.

Кристаллы бора имеют форму икосаэдра

Звёздчатые формы икосаэдра

Икосаэдр имеет двадцать граней. Если каждую из них продолжить неограниченно, то тело будет окружено великим многообразием отсеков - частей пространства, ограниченных плоскостями граней. Все звездчатые формы икосаэдра можно получить добавлением к исходному телу таких отсеков. Не считая самого икосаэдра, продолжения его граней отделяют от пространства 20+30+60+20+60+120+12+30+60+60 отсеков десяти различных форм и размеров. Большой икосаэдр состоит из всех этих кусков, за исключением последних шестидесяти. Среди звездчатых форм икосаэдра встречаются некоторые соединения Платоновых тел. Среди них: соединения пяти октаэдров, энантиоморфные формы соединения пяти тетраэдров и соединения десяти тетраэдров. Если бы Платон смог видеть эти формы, они привели бы его в восхищение. После того как были открыты эти и ряд других многогранников, ученые, естественно, задумались над вопросом: сколько существует звездчатых форм икосаэдра? В 1900 году Брюкнер опубликовал классическую работу о многогранниках, озаглавленную ";Vielecke und Vielflache";, в которой были представлены некоторые новые звездчатые формы икосаэдра. Открытием еще несколько форм мы обязаны Уиллеру(1924). В 1938 году систематическое и полное исследование вопроса провел Кокстер совместно с Дювалем, Флэзером, Петри. Для различения исходных форм и выделения характерных форм они применили правила ограничения, установленные Дж. Миллером. Кокстер доказал, что всего существует 59 звездчатых форм икосаэдра , из которых 32 обладают полной, а 27 неполной икосаэдральной симметрией (последнее обстоятельство дает возможность строить энантиоморфные им аналоги, которые имеют красивый и необычный вид).

Соединение пяти тетраэдров

Асимметричное и скошенное положение граней этого многогранника придаёт ему необычайно привлекательный вид.

Соединение десяти тетраэдров

Этот многогранник представляет собой комбинацию двух энантиоморфных (зеркальных) форм соединения пяти тетраэдров.

Первая звёздчатая форма икосаэдра

Эту модель делают из 20 частей, каждая из которых представляет собой невысокую т реугольную пирамиду без основания.

Вторая звёздчатая форма икосаэдра

На этой очень красивой модели заметны пятигранные высокие пики, выступающие из впадин модели соединения десяти тетраэдров.

Третья звёздчатая форма икосаэдра

Этот весьма простой многогранник принадлежит к семейству дельтаэдров . Для дельтаэдров характерно, что все их грани представляют собой равносторонние треугольники. Сам многогранник внешне напоминает додекаэдр и даже содержит его рёбра, но на самом деле является звёздчатой формой икосаэдра. Его можно представить себе как додекаэдр с удалёнными пятиугольными гранями, место которых заняли пятигранные впадины с п равильными треугольными гранями.

Четвёртая звёздчатая форма икосаэдра

Как уже отмечалось, процесс продолжения граней икосаэдра ведёт к появлению десяти различных типов отсеков, служащих дополнением к исходному телу. Модель одной из звёздчатых форм можно построить таким образом, что отсеки явятся как бы связками между вершинами некоторого многогранника. Эта модель представляет собой аналог скелетной модели правильного додекаэдра, роль рёбер которой выполняют наши отсеки.

Эта модель — первый пример многогранника с открытой внутренней частью.

Пятая звёздчатая форма икосаэдра

Многие звёздчатые формы икосаэдра внешне очень похожи на большой икосаэдр (который будет рассмотрен ниже). Пятая форма особенно интересна: она служит примером многогранника, вершины которого связаны только отсеками.

Шестая звёздчатая форма икосаэдра

Ещё одна звёздчатая форма икосаэдра. На ней легко обнаружить 12 длинных пиков, выступающих из впадин модели дельтаэдра (третья звёздчатая форма икосаэдра)

Седьмая звёздчатая форма икосаэдра

Этот многогранник состоит из 20 частей, каждая из которых имеет форму шестигранного невысокого пика

Восьмая звёздчатая форма икосаэдра

На рисунке показана модель звёздчатого икосаэдра, также весьма сходного с большим икосаэдром. В действительности наш многогранник можно представить в виде большого икосаэдра с удалёнными клинообразными частями, стягивающими основания вершинных частей.

Девятая звёздчатая форма икосаэдра

В предыдущих моделях пики были несколько короче, но эта состоит всего лишь из двенадцати таких пиков.

Десятая звёздчатая форма икосаэдра

Дальнейшее продолжение граней икосаэдра приводит к появлению нового типа отсеков — наклонных пиков. Это единственный тип отсеков, имеющих две энантиоморфные модификации; каждая из них состоит из 60 коротких трёхгранных пирамидок. По существу пики этого многогранника образуют рёбра модели соединения пяти тетраэдров, встречаясь по три в каждой вершине тетраэдров и по два в остальных угловых точках на поверхности соединения.

Одиннадцатая звёздчатая форма икосаэдра

В изготовлении эта модель гораздо проще предыдущей.

Двенадцатая звёздчатая форма икосаэдра

Тринадцатая звёздчатая форма икосаэдра

На фотографии показана модель красивого многогранника с 12 длинными пиками, основание каждого из которых окружено пятью более короткими пиками. Эти части легко узнать — они уже встречались в предыдущих формах.

Четырнадцатая звёздчатая форма икосаэдра

Этот многогранник, весьма эффектный благодаря оригинальным скошенным граням, обладает обычной симметрией додекаэдра, но характерен большими пятиугольными отверстиями, пронизывающими его насквозь и о ставляющими как бы открытым изнутри.

Пятнадцатая звёздчатая форма икосаэдра

Из описанных выше многогранников – звёздчатых форм икосаэдра, пожалуй, самым красивым и декоративным является большой икосаэдр — последний из четырёх правильных звёздчатых многогранников Кеплера — Пуансо. Его вершины представляют собой центры правильных пятиугольных звёзд, выступающих из тела многогранника. Это свойство роднит большой икосаэдр с большим додекаэдром и выделяет эти два тела из всего множества однородных многогранников. Многие однородные многогранники имеют звёздчатые грани, но подобного строения вершин больше не встречается.

Завершающая звёздчатая форма икосаэдра

Показанный на фотографии многогранник — завершающая звёздчатая форма икосаэдра. Она образована присоединением к нему (икосаэдру) в с е х отсеков, получаемых при продолжении граней икосаэдра. Модель как бы ощетинена иглами, группирующимися по пять в красивые и отчётливо заметные гроздья. Вся модель состоит из 12 таких гроздьев.

Октаэдр – один из пяти правильных многогранников, имеющий 8 треугольных граней, 12 рёбер, 6 вершин. Каждая его вершина является вершиной четырёх треугольников. Сумма плоских углов при каждой вершине равна 240 градусов. Октаэдр имеет центр симметрии - центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.

Радиус описанной сферы

Радиус вписанной сферы

Октаэдр в головоломках: змея Генеля

Октаэдр в строении Вселенной, в изображениях на полях («круги на полях)

В 1997 и 1999 годах появились, по крайней мере, 9 кругов на полях, тесно связанных с обнаруженной формой Вселенной.

На рисунке показаны два близко расположенных октаэдра, наблюдаемых с положения нашего Солнца, рядом с точкой их соединения. На вершинах и углах форм обнаруживаются суперкластеры, каждый из которых может содержать миллиарды галактик, а также пустоты.

Т рехмерный октаэдр Овертона

Фотография Стива Александера

Западный Овертон, 24 июня 1999 года

Трудность демонстрации вращающихся твердых тел в символах кругов на полях состоит в том, чтобы изобразить в двух измерениях четыре (или более) измерений. Беря из этого круга на полях только пути (убирая маленькие шестиугольники и рассматривая большие шестиугольники как точки на линиях) и сворачивая по линиям, мы получаем трехмерный октаэдр.

В природе, в науке, в жизни этот многогранник встречается довольно часто: он находит применение в объяснении структуры и форм Вселенной, в строении ДНК и нанотехнологиях, в создании игр-головоломок… Но чаще всего он встречается, пожалуй, в первом – в природе. А именно, в строении кристаллов. Форму октаэдра имеют кристаллы алмаза, перовскита, оливина, флюорита, шпинели, алюминиево-калиевых квасцов, медного купороса и даже хлорида натрия и золота!

Октаэдр в природе: кристаллы в форме октаэдра

А люминиево-калиевые квасцы

Звёздчатая форма октаэдра

Ещё одна особенность октаэдра – его звёздчатая форма, поскольку, в отличие от других многогранников, она у него всего одна. Это геометрическое тело описал в 1619 году Иоганн Кеплер и назвал его stella octangula (восьмиугольная звезда). Звездчатый октаэдр - это восемь пересекающихся плоскостей граней октаэдра, образующих в пространстве столько же новых отсеков в форме тетраэдров, основания которых совпадают с гранями октаэдра. Его можно рассматривать как соединение двух пересекающихся тетраэдров, центры которых совпадают с центром исходного октаэдра. Все вершины звездчатого октаэдра совпадают с вершинами некоторого куба, а ребра его являются диагоналями граней (квадратов) этого куба. Дальнейшее продление граней октаэдра не приводит к созданию нового многогранника, поэтому он имеет только одну звездчатую форму.

В результате выполненной работы мы познакомились с интереснейшим, красивейшим, загадочным миром многогранников. Подробно рассмотрели такие правильные многогранники, как икосаэдр и октаэдр, выявили их связь с природой. Выполнили модели некоторых звёздчатых форм икосаэдра и октаэдра.

Икосаэдр — правильный выпуклый многогранник, двадцатигранник, один из тел Платона.

Ранее мы писали о додекаэдре , сейчас поговорим о другом похожем двадцатиграннике – икосаэдре .

Все 20 граней являются равносторонними треугольниками. количество ребер

соответствует 30, количество вершин — 12. Икосаэдр состоит из 59

Все 12 вершин икосаэдра являются вершинами 5 равносторонних

треугольников, значит, сумма углов у вершины = 300°.

У икосаэдра 30 ребер. Как и у всех правильных многогранников ребра икосаэдра имеют равную длину,

а грани - равную площадь.

У икосаэдра, как и додекаэдра, 15 осей симметрии, все проходят через

середины противолежащих параллельных ребер. Точка пересечения этих

осей икосаэдра – это и есть его центр симметрии.

Так же как и у додекаэдра, у икосаэдра 15 плоскостей симметрии.

Плоскости симметрии проходят через четыре вершины, которые лежат в

одной плоскости, и середины противоположных параллельных ребер.

Пусть длина ребра икосаэдра будет а тогда:

Сумма длин всех ребер:

Площадь икосаэдра:

Объем икосаэдра:

Радиус вписанной в икосаэдр сферы:

Радиус описанной вокруг икосаэдра сферы:

Свойства икосаэдра.

• Каждая из 12 вершин икосаэдра лежит по 3 в 4-х параллельных плоскостях, образуя во всех

• 10 вершин икосаэдра находятся в 2-х параллельных плоскостях, и образуют в них 2 правильных

5-ти угольника, а оставшиеся 2 — противоположны друг другу и находятся в 2-х концах диаметра

описанной вокруг икосаэдра сферы, который перпендикулярен параллельным плоскостям.

• Икосаэдр возможно вписать в куб, тогда 6 взаимо-перпендикулярных ребер икосаэдра будут

находиться соответственно на 6-ти гранях куба, оставшиеся 24 ребра находятся внутри куба, все 12

вершин икосаэдра будут находиться на ше6-ти гранях куба.

• В икосаэдр можно вписать тетраэдр, таким образом, чтобы 4 вершины тетраэдра станут

совмещены с 4-мя вершинами икосаэдра.

• Икосаэдр возможно вписать в додекаэдр, тогда вершины икосаэдра совместятся с центрами

• В икосаэдр возможно вписать додекаэдр с совмещением вершин додекаэдра и центров граней

• Усечённый икосаэдр можнополучить, срезав 12 вершин с образованием граней вида правильных

5-ти угольников. Тогда количество вершин нового многогранника увеличится в 5 раз (12×5=60), 20

треугольных граней становятся правильными шестиугольниками (количество граней

теперь 20+12=32), а рёбер - 30+12×5=90.

• Сделать икосаэдра можно из 20 тетраэдров.

• Нельзя сделать икосаэдр из правильных тетраэдров, потому что радиус описанной сферы вокруг

икосаэдра и длина бокового ребра (вершины-центр такой сборки) тетраэдра меньше ребра икосаэдра.

Усечённый икосаэдр.

Усечённый икосаэдр — это многогранник, который состоит из 12 правильных 5-ти угольников и 20

правильных 6-ти угольников. У усеченного икосаэдра икосаэдрический тип симметрии.

Примеры икосаэдров в мире:

• Обычный футбольный мяч является усечённым икосаэдром.

• Капсиды большинства вирусов (например, бактериофаги, мимивирус).

Молекула фуллерена C60 — усечённый икосаэдр.

Развертка икосаэдра.

Как сделать икосаэдр.

Способ № 1 Икосаэдр из заготовки

Распечатываем готовое изображение развертки икосаэдра, вырезаем и склеиваем по границам. Далее

на ваше усмотрение окрашиваете в любой цвет и украшаете.

Способ № 2 Икосаэдр своими руками

Вам понадобится бумага, карандаш, линейка (удобней будет циркуль), ножницы, клей ПВА (или другой).

При помощи линейки, циркуля и карандаша рисуем на бумаге несколько треугольников (как на рисунке

ниже). Чтоб было легче, можете нарисовать 5 параллелограммов, а после каждый прямоугольник

разделить на 4 равносторонних треугольника. Далее вырезаем, оставив места для склейки и

Вирусы и бактерии играют важную роль в жизни людей, являясь в основном возбудителями различных заболеваний. Для осенне-весеннего периода характерен рост инфекционных заболеваний, вызванных данными мельчайшими формами жизнь.

Изучить видовое многообразие форм вирусов и бактерий, сравнить их формы и пространственное расположение с геометрическими фигурами, исследовать процесс размножения вирусов и бактерий с математической точки зрения.

Изучить геометрические формы и пространственное расположение отдельных представителей вирусов и бактерий.

Изучить рост численности и размеры выбранных микроорганизмов.

Доказать, что рост численности вирусов и бактерий подчиняется законам математике.

Вирусы и бактерии.

Геометрические формы и пространственное расположение вирусов и бактерий, скорость их размножения.

Вирусы можно представить в виде идеальных геометрических тел, а бактерии – в виде поверхностей вращения. Скорость размножения вирусов и бактерий в идеальных условиях можно описать, используя математические законы.

Актуальность исследования обусловлена тем, что людей окружает множество различных микроорганизмов, большую часть из которых составляют вирусы и бактерии. Многие из них опасны для человека. Эти микроскопические организмы могут вызывать заболевания, как у людей, так и у животных, растений, грибов, причём каждый из них имеет своего собственного специфического хозяина. Лишь часть микроорганизмов полезны для организма человека, например, молочнокислые бактерии, азотофиксирующие бактерии, бактериофаги (вирусы, избирательно поражающие бактериальные клетки).

Скорость размножения этих примитивных форм жизни чрезвычайно велика и зависит не только от условий, в который попали эти микроорганизмы, но и от их строения и пространственного расположения.

Поэтому, для борьбы с опасными вирусами и бактериями необходимо иметь представления об их строении, форме, пространственном расположении, особенностях и скорости размножения.

Первыми организмами, появившимися на Земле несколько миллиардов лет назад и создавшими предпосылки для дальнейшего развития жизни, были бактерии. Сейчас они составляют отдельное царство живых организмов. Вирусы – самые мелкие из известных живых существ. Бактерии являются самостоятельными живыми организмами, вирусы же, не имеющие собственного обмена веществ, заимствуют свою жизнь у клеток растений, животных и бактерий. Они являются внутриклеточными паразитами живых организмов и не способны размножаться вне клетки. Вне клетки вирусные частицы ведут себя как химические вещества.

Вирусы – простейшая форма жизни

Вирус (от латинского virus – яд) – простейшая форма жизни, микроскопическая частица, представляющая собой молекулы нуклеиновых кислот (ДНК или РНК), заключенные в белковую оболочку (капсид) и способные инфицировать живые организмы. Некоторые вирусы, такие как мимивирусы, имеют оба типа молекул. В среднем, вирусы в 5 раз меньше бактерий. Размеры и формы вирусов разнообразны. Большинство изученных вирусов имеют диаметр в пределах от 20 до 300 нм. Некоторые филовирусы имеют длину до 1400 нм, но их диаметр составляет лишь 80 нм. В 2013 году самым крупным из известных вирусов считался Pandoravirus размерами 1 × 0,5 мкм, однако в 2014 году из многолетней мерзлоты из Сибири был описан Pithovirus, достигающий 1,5 мкм в длину и 0,5 мкм в диаметре. В настоящий момент он считается крупнейшим из известных вирусов. Большинство вирионов невозможно увидеть в световой микроскоп, поэтому используют электронные – как сканирующие, так и просвечивающие.

Зрелая вирусная частица, состоит из нуклеиновой кислоты, покрытой защитной белковой оболочкой – капсидом. Капсомер – структурная белковая субъединица капсида. Капсид состоит из белков, а его форма лежит в основе классификации вирусов по морфологическому признаку.

Типы капсидов вирусов

Классифицируют четыре морфологических типа капсидов вирусов: икосаэдрический, спиральный, продолговатый и комплексный.

Икоса́эдр – правильный выпуклый многогранник, двадцатигранник , одно из Платоновых тел. Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин – 12. Икосаэдр имеет 59 звёздчатых форм (рис. 1).

Рисунок 1. Геометрическая модель икосаэдра.

Большинство вирусов животных имеют икосаэдрическую или почти шарообразную форму с икосаэдрической симметрией. Правильный икосаэдр является оптимальной формой для закрытого капсида, сложенного из одинаковых субъединиц. Минимальное необходимое число одинаковых капсомеров – 12, каждый капсомер состоит из пяти идентичных субъединиц. Многие вирусы, такие как ротавирус (вирус кишечного гриппа), имеют более двенадцати капсомеров и выглядят круглыми, но сохраняют икосаэдрическую симметрию.

Вирион аденовирусов имеет форму правильного икосаэдра (диаметр 80-100 нм) со скругленными рёбрами. В каждой вершине имеется выступающая белковая структура, необходимая для связывания с клеточными рецепторами заражаемых клеток. Внутри частицы упакован геном вируса, представленный линейной двуцепочечной ДНК, длина которой варьируется, но в среднем составляет 35000 пар нуклеотидов. Капсид состоит из двух видов капсомеров – гексонов (240 гексонов) с шестью рядом располагающимися частицами и 12 пентонов на вершине икосаэдра, соединяющиеся с пятью соседними частицами (рис. 3)

Рисунок 2. Схема строения аденовируса.

Вирус папилломы человека представляет собой кольцевую двухцепочечную молекулу ДНК протяженностью около 8000 пар нуклеотидов, покрытую белковым капсидом. Капсид имеет форму икосаэдра и сформирован 72 пентамерами протеина L1, с которыми ассоциирован протеин L 2 (рис. 3)

Рисунок 3. Вирус папилломы человека.

Вирус краснухи имеет сферическую форму, диаметром 50-70 нм. Это сложный РНК-геномный вирус. РНК заключена в капсид икосаэдрической симметрии, состоящей из С белка. Нуклеокапсид окружен оболочкой – липидным бислоем – суперкапсидом (рис. 4).

Рисунок 4. Строение вируса краснухи.

Вирус кори – сложно организованный вирус, его диаметр составляет от 150 до 350 нм (рис. 5), это наиболее крупный РНК-содержащий вирус человека и животных. Белковый капсид вируса устроен по икосаэдрическому типу симметрии и содержит геном, представленный одной линейной отрицательной нитью рибонуклеиновой кислоты (РНК) – 1Н(–)РНК.

Рисунок 5. Схема строения вируса кори.

Вирус полиомиелита полиовирус является представителем мелких фильтрующихся вирусов. Его размер составляет от 15 до 30 нм, масса – 8-9 МД. Полиовирусы имеют сферическую форм, икосаэдрический тип симметрии. Внутри располагается однонитчатая плюс-РНК и протеин VPg. Генетический материал вируса защищен снаружи капсидом. РНК составляет 20-30% очищенного вируса, состоит из 7,5-8 тысяч нуклеотидов. Молекулярная масса РНК составляет 2,5 МД. Капсид состоит из 12-и пентамеров (пятиугольников). Каждый из пентамеров состоит из 5 протомеров – белковых субъединиц. Внешняя оболочка отсутствует (рис. 6).

Рисунок 6. Вирус полиомиелита.

Спиральные капсиды устроены несколько проще. Капсомеры, составляющие капсид, покрывают спиральную нуклеиновую кислоту и формируют тоже достаточно стабильную белковую оболочку этих вирусов. И при использовании высокоразрешающих электронных микроскопов и соответствующих методов приготовления препарата можно видеть спирализованные структуры на вирусах. При спиральной симметрии капсида вирусная нуклеиновая кислота образует спиральную (или винтообразную) фигуру, полую внутри, и субъединицы белка (капсомеры) укладываются вокруг нее тоже по спирали (трубчатый капсид) (рис. 7). Примером вируса со спиральной симметрией капсида является вирус табачной мозаики, который имеет палочковидную форму, а его длина составляет 300 нм с диаметром 15 нм. В состав вирусной частицы входит одна молекула РНК размером около 6000 нуклеотидов. Капсид состоит из 2000 идентичных субъединиц белка, уложенных по спирали.

Рисунок 7. Строение вируса табачной мозаики.

Рисунок 8. Бактериофаг.

Продолговатыми назыают икосаэдрические капсиды, вытянутые вдоль оси симметрии пятого порядка. Такая форма характерна для головок бактериофагов (рис. 8).

Рисунок 9. Строение бактериофага Т4.

К омплексный капсид, организованный по принципу двойной симметрии. Некоторые бактериофаги имеют двойную симметрию: головка организована по принципу кубической симметрии, отросток - по принципу спиральной симметрии. Форма этих капсидов ни чисто спиральная, ни чисто икосаэдрическая. Они могут нести дополнительные наружные структуры, такие как белковые хвосты или сложные наружные стенки. Некоторые бактериофаги, такие как фаг Т4, имеют комплексный капсид, состоящий из икосаэдрической головки, соединённой со спиральным хвостом, который может иметь шестигранное основание с отходящими от него хвостовыми белковыми нитями. Этот хвост действует наподобие молекулярного шприца, прикрепляясь к клетке-хозяину и после впрыскивая в неё генетический материал вируса (рис. 9).

Вирусы по своей форме напоминают идеальные геометрические тела – многогранники, сферу.

Рисунок 10. Бактериальная клетка.

Б актерии – обширная группа одноклеточных микроорганизмов, характеризующихся отсутствием окруженного оболочкой клеточного ядра. Генетический материал бактерии (дезоксирибонуклеиновая кислота, или ДНК) занимает в клетке вполне определенное место - зону, называемую нуклеоидом (рис. 10).

По форме клеток бактерии можно разделить на несколько групп: палочковидные бациллы, сферические кокки, спиральные спириллы, вибрионы(короткие палочки, всегда изогнутые в виде запятой) (рис. 11).

Рисунок 11. Форма бактерий.

Кокковидные бактерии обычно имеют форму правильного шара, диаметром 1,0-1,5 мкм; некоторые бобовидную, ланцетовидную, эллипсовидную форму. По характеру взаиморасположения образующихся после деления клеток кокки подразделяют на следующие группы:

Микрококки (от лат. мicros – малый). Клетки делятся в одной плоскости и чаще всего сразу же отделяются от материнской. Располагаются по одиночке, беспорядочно. Сапрофиты, патогенных для человека нет (рис. 12).

Рисунок 12. Микрококки.

Рисунок 13. Диплококки.

Д иплококки (от лат. diplos – двойной). Деление происходит в одной плоскости с образованием пар клеток, имеющих либо бобовидную, либо ланцетовидную форму. Например, возбудитель гонореи Neisseria gonorrhoeae, возбудитель пневмонии Streptococcus pneumoniae (рис. 13).

Рисунок 14. Стрептококки.

С трептококки (от лат. streptos – цепочка). Деление клеток происходит в одной плоскости, но размножающиеся клетки сохраняют между собой связь и образуют различной длины цепочки, напоминающие нити бус. Многие стрептококки являются патогенными для человека и вызывают различные заболевания: скарлатину, ангину, гнойные воспаления и другие. Например, Streptococcus pyogenes (рис. 14).

Стафилококки (от лат. staphyle – гроздь винограда). Клетки делятся в нескольких плоскостях, а образующиеся клетки располагаются скоплениями, напоминающими гроздья винограда. Стафилококки вызывают более 100 различных заболеваний человека. Они наиболее частые возбудители гнойных воспалений. Например, Staphylococcus aureus (рис. 15).

Рисунок 15. Золотистый стафилококк.

Рисунок 16. Тетракокки.

Т етракокки (от лат. tetra – четыре). Деление происходит в двух взаимно перпендикулярных плоскостях с образованием тетрад. Патогенные для человека виды встречаются очень редко (рис. 16).

Рисунок 17. Сарцины.

С арцины (от лат. sarcina – связка, тюк). Деление происходит в трех взаимно перпендикулярных плоскостях с образованием пакетов (тюков) из 8, 16, 32 и большего числа особей. Особенно часто встречаются в воздухе (рис. 17).

Рисунок 18. Палочковидные бактерии.

Цилиндрическая, или палочковидная форма характерна для большинства бактерий (греч. bacteria – палочка; лат. bacillum – палочка). Палочковидные бактерии подразделяются на образующие эндоспоры и не образующие эндоспоры. Палочковидные бактерии различаются по длине, поперечному диаметру, форме концов клеток, расположению (рис. 18).

Эти формы различаются количеством и характером завитков, длиной и толщиной клеток. Они подразделяются на вибрионы (лат. vibrare – колебание, дрожание), которые имеют вид изогнутой палочки или запятой (рис. 19); спириллы(лат. spiro – изгиб) – это спирально изогнутые клетки, имеющие большой поперечный диаметр и малое число высоких завитков (рис. 20); спирохеты (лат. spiro – изгиб, греч. сhaite – хохол, грива) (рис. 21) – это изгибающиеся тонкие спирально изогнутые клетки, напоминающие по форме синусоиду (рис. 22).

Рисунок 19. Вибрионы

Рисунок 20. Спириллы.

Рисунок 21. Бледная трепонема.

Рисунок 22. Синусоида.

Рост численности вирусов и бактерий

Рисунок 23. Репродукция вируса.

Размножение вирусов протекает с исключительно высокой скоростью: так при попадании в верхние дыхательные пути одной вирусной частицы вируса гриппа уже через 8 часов количество инфекционного потомства достигает 10³, а концу первых суток – 10²³. Высочайшая скорость размножения вируса гриппа объясняет столь короткий инкубационный период 1-2 суток. Быстроте репродукции вируса благоприятствует распространение многих сотен вирионов, подготовленных лишь одной зараженной клеткой.

Цикл репродукции аденовируса продолжается 14 и более часов. В одной клетке образуется до 1000 вирусных частиц, при этом клетка разрушается. В свою очередь новые вирусные частицы, попав в новые клетки, становятся способными к созданию других вирионов и т.д. Таким образом только один вирион через двое суток после попадания в клетку человека способен дать потомство около 1 млрд. вирионов. То есть размножение вируса подчиняется формуле n-ого члена геометрической прогрессии, где, где q = 1000.

Геометрическая прогрессия – последовательность чисел ( членов прогрессии ) b ₁, b _2, b ₃,…, в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число q ( знаменатель прогрессии ), где b ₁ ≠ 0, q ≠ 0, b ₂= b ₁ q , b ₃= b ₂ q ,…, b _n = b _{n -1} q

Бактерии в благоприятных условиях растут очень быстро. Как простейшие одноклеточные организмы, бактерии размножаются делением. Достигая своих максимальных габаритов, клетка начинает процесс деления. Спустя определённое время, одна бактерия разделившись по середине, оставляет одну свою полноценную и самостоятельную копию. В благоприятной среде процесс деления протекает особенно динамично. Попадая в благоприятные для развития условия, бактерия делится, образуя две дочерние клетки; у некоторых бактерий деления повторяются через каждые 20 минут и возникают все новые и новые поколения бактерий. Произведём некоторые расчёты, составим числовую последовательность из получившегося числа бактерий: 1, 2, 4, 8, 16, 32, 64… . Заметим, что данная последовательность образует геометрическую прогрессию со знаменателем, равным 2. Отметим, что через час четвёртый член последовательности будет равен 8, через 2 часа – седьмой член последовательности будет равен 64 и т.д. Через 6 часов 19-ый член такой прогрессии будет равен 262144 и т.д. (рис. 24).

Рисунок 24. Размножение бактерий делением надвое.

Бактерии и вирусы представляют собой геометрические тела, поверхности которых используются с наибольшей выгодой для проникновения в клетки человека: бактерии- сферические, спиралевидные, палочковидные клетки, снабжённые несколькими жгутиками, что позволяет быстро передвигаться; вирусы – принимают форму додекаэдра и икосаэдра, которые представляют собой лучшее приближение к сфере.

Размножение вирусов и бактерий подчиняется законам геометрической прогрессии, что тобусловливает высокую скорость распространения инфекционных заболеваний.

Голубев Д.Б. Размышления и споры о вирусах [Текст] / Д.Б. Голубев, В.З. Солоухин – М.: Молодая гвардия, 1989. – 226с.

Лысак В.В. Микробиология [Текст] / В.В. Лысак. – Минск.: БГУ, 2007. – 426 с.; ISBN 985-485-709-3.

Орлова О.Г. Morbillivirus – вирус кори. Общая характеристика и диагностика инфекции [Текст] / О.Г. Орлова, О.В. Рыбальченко, Е.М. Ермоленко. – СПб.: СпецЛит, 2014. – 32с; ISBN: 978-5-299-00620-9