21 задание огэ по математике шпоры
Решение уравнений
В данном задании необходимо решить уравнение степени больше двух — это может быть биквадратное или кубическое уравнение. Ниже мы приводим алгоритмы решения типовых заданий!
- Определить тип уравнения.
- Перенести правую часть уравнения в левую.
- Привести уравнение к виду, при котором можно его многочлен слева разложить на множители.
- Разложить на множители.
- Приравнять каждый множитель к нулю
- Решить полученные уравнения.
- Записать ответ.
1. Уравнение четвертой степени.
2. Перенесем правую часть уравнения в левую:
x 4 — (4x — 5) 2 = 0
3. Уравнение уже приведено к виду, при котором можно его левую часть разложить на множители.
4. Данное уравнение разложим на множители по формуле разности квадратов. Получим:
(х 2 – (4х-5))( х 2 + (4х-5)) = 0, или (х 2 – 4х+5)(х 2 + 4х-5) = 0.
5. Приравняем каждый множитель к нулю:
х 2 – 4х+5 = 0 и х 2 + 4х-5 = 0
6. Решим каждое из уравнений по формулам дискриминанта и корней:
Для первого уравнения:
D = b 2 -4ac = 16-20 = — 4, это означает, что первое уравнение х 2 – 4х+5 = 0 не имеет корней.
Для второго уравнения:
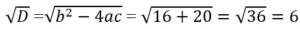
Определим корни второго уравнения:
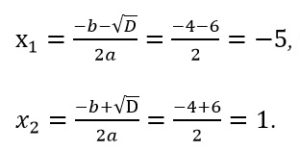
Получили два корня: -5; 1.
- Определить тип уравнения.
- Найти делители свободного члена уравнения.
- Определить среди делителей один из корней.
- Выполнить деление кубического многочлена на выражение х-а, где а – найденный корень.
- Записать получившийся в результате деления квадратный трехчлен и составим уравнение.
- Решить уравнение.
- Записать ответ.
1. Перед нами уравнение третьей степени общего типа.
2. Найдем делители свободного члена данного уравнения. Это числа: 1; -1; 2; -2; 3; -3; 4; -4; 6; -6; 12; -12;.18; -18; 36; -36.
3. Рассмотрим числа 1; -1; 2; -2; 3; -3. Это наименьшие среди найденных делителей. Подставим их по очереди в уравнение вместо х:
Мы нашли один корень.
4. Теперь выполним деление кубического многочлена на x-3, воспользовавшись схемой Горнера, имеем:
| 1 | 4 | -9 | -36 | |
| 3 | 1 | 7 | 12 | 0 |
Искать квадратный трехчлен можно другим способом, выполнив деление многочлена столбиком:
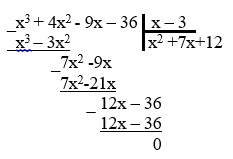
5. После деления получаем квадратный трехчлен:
Составим квадратное уравнение для вычисления оставшихся двух корней:
6. Решим его с помощью формул корней и дискриминанта
7. Получили три корня 3; -3; -4.
- Определить тип уравнения.
- Найти делители свободного члена уравнения.
- Определить среди делителей один из корней.
- Выполнить деление кубического многочлена на выражение х-а, где а – найденный корень.
- Записать получившийся в результате деления квадратный трехчлен и составим уравнение.
- Решить уравнение.
- Записать ответ.
1. Перед нами кубическое уравнение общего вида.
2. Найдем делители свободного члена уравнения. Это числа: 1; -1 и 2; -2.
3. Определим один из корней кубического уравнения среди делителей свободного члена .Для этого подставим каждый из этих делителей вместо x и проверим, какой их них является корнем:
4. Теперь выполним деление кубического многочлена на x-1, воспользовавшись схемой Горнера, имеем:
| 1 | 2 | -1 | -2 | |
| 1 | 1 | 3 | 2 | 0 |
Искать квадратный трехчлен можно другим способом, выполнив деление многочлена столбиком:
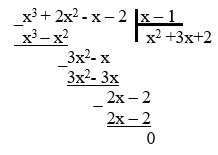
5. Получаем квадратный трехчлен
6. Составим и решим квадратное уравнение для вычисления оставшихся двух корней. Для этого воспользуемся формулами корней квадратного уравнения и дискриминантом.
7. Получили три корня -2; -1; 1.
Ответ: -2; -1; 1.
- Выполняем замену выражения с х на альтернативную переменную. Это позволит упростить уравнение и привести его к форме обычного квадратного.
- Решаем полученное квадратное уравнения.
- Переходим обратно к выражению с х, для которого была выполнена замена.
- Находим искомые корни уравнения.
Это уравнение можно решить с помощью т.Виета. Согласно теореме, имеем:
Возвращаемся к переменной х. Поскольку (х–2) 2 =а, то получим:

это уравнение корней не имеет, т.к. нельзя извлечь корень из отрицат.числа
Ответ: 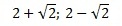
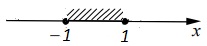
Решите систему уравнений
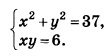
- Из 2-го уравнения выражаем у через х.
- Подставляем полученное выражение для у в 1-е уравнение.
- В полученном ур-нии с одной переменной (х) выполняем тождественные преобразования. Приводим его к квадратичному виду.
- Выполняем замену х 2 на а. Решаем полученное квадратное ур-ние.
- Возвращаемся от а к х. Находим все значения (корни) для х.
- Определяем соответствующие им значения для у.
- Фиксируем в ответе пары соответствующих корней.
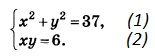
Из (2) выражаем у через х:
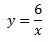
Полученное выражение для у подставляем в (1):
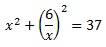
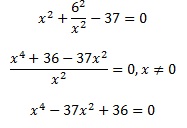
Теперь возвращаемся к уравнению, в котором у выражено через х. И вычисляем соответствующие значения для у:
Выберите книгу со скидкой:

Математика. Сложение и вычитание. Уровень 3 Kumon
350 руб. 472.00 руб.

Математика. Готовлюсь к школе с наклейками
350 руб. 130.00 руб.

Математика. Новый полный справочник школьника для подготовки к ЕГЭ
350 руб. 222.00 руб.

СПЛОШНОЕ УЧЕНИЕ. ЗАНИМАТЕЛЬНАЯ МАТЕМАТИКА
350 руб. 204.00 руб.

Смешная математика (математика с наклейками)
350 руб. 56.00 руб.

Посчитаем, поиграем (математика с наклейками)
350 руб. 56.00 руб.

Математика до школы (математика с наклейками)
350 руб. 56.00 руб.

МОЯ РАБОЧАЯ ТЕТРАДЬ. ПЕРВАЯ МАТЕМАТИКА
350 руб. 35.00 руб.

Все формулы мира: Как математика объясняет законы природы
350 руб. 980.00 руб.

Математика космоса: Как современная наука расшифровывает Вселенную
350 руб. 860.00 руб.

350 руб. 116.00 руб.

Игра случая: математика и мифология совпадения
350 руб. 600.00 руб.
БОЛЕЕ 58 000 КНИГ И ШИРОКИЙ ВЫБОР КАНЦТОВАРОВ! ИНФОЛАВКА



- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы
- Юргенсон Вероника АлександровнаНаписать 38709 05.04.2016
Номер материала: ДБ-011356
- Другое
- 9 класс
- Другие методич. материалы
Добавляйте авторские материалы и получите призы от Инфоурок
Еженедельный призовой фонд 100 000 Р
-
05.04.2016 371
-
05.04.2016 4282
-
05.04.2016 819
-
05.04.2016 3245
-
05.04.2016 2683
-
05.04.2016 1494
-
05.04.2016 517
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Формулы, правила, свойства. Можно использовать для сдачи ЕГЭ и ОГЭ по математике.
Для начала шпаргалка в компактном виде:
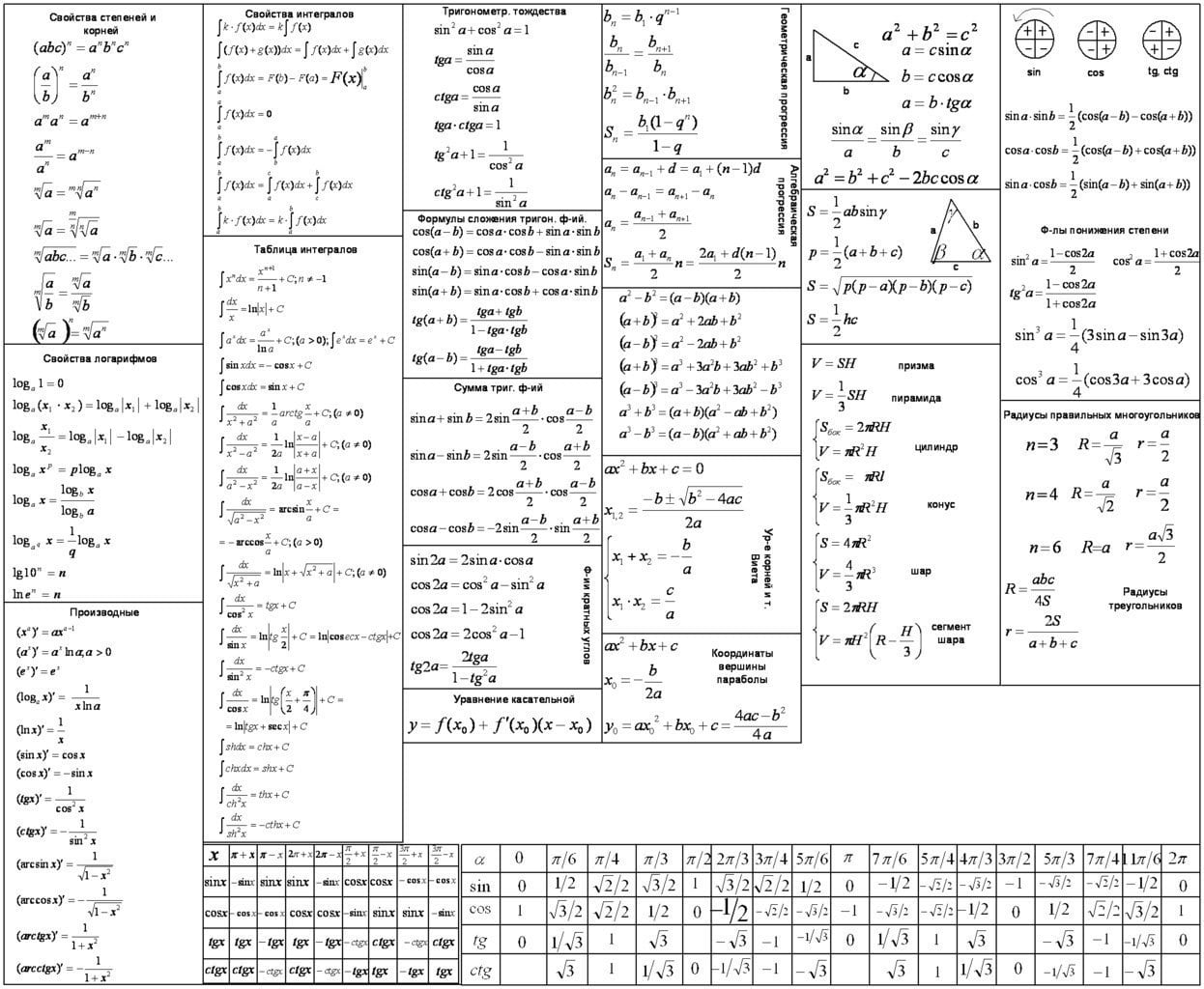
Формулы сокращенного умножения
(а+b) 2 = a 2 + 2ab + b 2
(а-b) 2 = a 2 – 2ab + b 2
a 3 – b 3 = (a-b)( a 2 + ab + b 2 )
a 3 + b 3 = (a+b)( a 2 – ab + b 2 )
(a + b) 3 = a 3 + 3a 2 b+ 3ab 2 + b 3
(a – b) 3 = a 3 – 3a 2 b+ 3ab 2 - b 3
Свойства степеней
a m/n = (a≥0, n ε N, m ε N)
a - r = 1/ a r (a>0, r ε Q)
a m · a n = a m + n
a m : a n = a m – n (a≠0)
Первообразная
Если F’(x) = f(x), то F(x) – первообразная
x n = x n +1 /n+1 + C
a x = a x / ln a + C
cos x = sin x + C
1/ sin 2 x = – ctg x + C
1/ cos 2 x = tg x + C
sin x = – cos x + C
Геометрическая прогрессия
q – знаменатель прогрессии
b n = b1 · q n – 1 – n-ый член прогрессии
Модуль
-a, если a Формулы cos и sin
sin (x + π) = -sin x
cos (x + π) = -cos x
sin (x + 2πk) = sin x
cos (x + 2πk) = cos x
sin (x + π/2) = cos x
Объемы и поверхности тел
1. Призма, прямая или наклонная, параллелепипед V = S·h
2. Прямая призма SБОК = p·h, p – периметр или длина окружности
3. Параллелепипед прямоугольный
V = a·b·c; P = 2(a·b + b·c + c·a)
P – полная поверхность
4. Куб: V = a 3 ; P = 6 a 2
S = 1/3 S·h; S – площадь основания
6. Пирамида правильная S =1/2 p·A
A – апофема правильной пирамиды
7. Цилиндр круговой V = S·h = πr 2 h
8. Цилиндр круговой: SБОК = 2 πrh
9. Конус круговой: V=1/3 Sh = 1/3 πr 2 h
10. Конус круговой: SБОК = 1/2 pL= πrL
Тригонометрические уравнения
sin x = 1, x = π/2 + 2 πn
sin x = -1, x = – π/2 + 2 πn
cos x = 0, x = π/2 + 2 πn
cos x = 1, x = 2πn
cos x = -1, x = π + 2 πn
Теоремы сложения
cos (x +y) = cosx ·cosy – sinx ·siny
cos (x -y) = cosx ·cosy + sinx ·siny
sin (x +y) = sinx ·cosy + cosx ·siny
sin (x -y) = sinx ·cosy – cosx ·siny
tg (x ±y) = tg x ± tg y/ 1 - + tg x ·tg y
ctg (x ±y) = tg x - + tg y/ 1± tg x ·tg y
sin x ± sin y = 2 cos (x±y/2)· cos (x - +y/2)
cos x ± cosy = -2 sin (x±y/2)· sin (x - +y/2)
1 + cos 2x = 2 cos 2 x; cos 2 x = 1+cos2x/2
1 – cos 2x = 2 sin 2 x; sin 2 x = 1- cos2x/2
a,b – основания; h – высота, c – средняя линия S = (a+b/2)·h = c·h
а – сторона, d – диагональ S = a 2 = d 2 /2
a – сторона, d1, d2 – диагонали, α – угол между ними S = d1d2/2 = a 2 sinα
9. Правильный шестиугольник
a – сторона S = (3√3/2)a 2
S = (L/2) r = πr 2 = πd 2 /4
Правила дифференцирования
( f (x) + g (x) )’ = f ’(x) + g’(x)
(tg x)’ = 1/ cos 2 x
(ctg x)’ = – 1/ sin 2 x
(f (kx + m))’ = kf ’(kx + m)
Уравнение касательной к графику функции
Площадь S фигуры, ограниченной прямыми x = a , x = b
Формула Ньютона-Лебница
| t | π/4 | π/2 | 3π/4 | π |
| cos | √2/2 | 0 | -√2/2 | 1 |
| sin | √2/2 | 1 | √2/2 | 0 |
| t | 5π/4 | 3π/2 | 7π/4 | 2π |
| cos | -√2/2 | 0 | √2/2 | 1 |
| sin | -√2/2 | -1 | -√2/2 | 0 |
| t | 0 | π/6 | π/4 | π/3 |
| tg | 0 | √3/3 | 1 | √3 |
| ctg | - | √3 | 1 | √3/3 |
sin x = b x = (-1) n arcsin b + πn
cos x = b x = ± arcos b + 2 πn
tg x = b x = arctg b + πn
ctg x = b x = arcctg b + πn
Теорема синусов : a/sin α = b/sin β = c/sin γ = 2R
Теорема косинусов : с 2 =a 2 +b 2 -2ab cos y
Неопределенные интегралы
∫ x n dx = (x n +1 /n+1) + C
∫ sin x dx = – cos x + C
∫ cos x dx = sin x + C
∫ dx/sin 2 x = -ctg + C
∫ dx/cos 2 x = tg + C
∫ x r dx = x r+1 /r+1 + C
Логарифмы
| Градус | 0 | 30 | 45 | 60 |
| sin | 0 | 1/2 | √2/2 | √3/2 |
| cos | 1 | √3/2 | √2/2 | 1/2 |
| tg | 0 | √3/3 | 1 | √3 |
| t | π/6 | π/3 | 2π/3 | 5π/6 |
| cos | √3/2 | 1/2 | -1/2 | -√3/2 |
| sin | 1/2 | √3/2 | √3/2 | 1/2 |
| 90 | 120 | 135 | 150 | 180 |
| 1 | √3/2 | √2/2 | 1/2 | 0 |
| 0 | -1/2 | -√2/2 | -√3/2 | -1 |
| - | -√3 | -1 | √3/3 | 0 |
| t | 7π/6 | 4π/3 | 5π/3 | 11π/6 |
| cos | -√3/2 | -1/2 | 1/2 | √3/2 |
| sin | -1/2 | -√3/2 | -√3/2 | -1/2 |
Формулы двойного аргумента
cos 2x = cos 2 x – sin 2 x = 2 cos 2 x -1 = 1 – 2 sin 2 x = 1 – tg 2 x/1 + tg 2 x
sin 2x = 2 sin x · cos x = 2 tg x/ 1 + tg 2 x
tg 2x = 2 tg x/ 1 – tg 2 x
ctg 2x = ctg 2 x – 1/ 2 ctg x
sin 3x = 3 sin x – 4 sin 3 x
cos 3x = 4 cos 3 x – 3 cos x
tg 3x = 3 tg x – tg 3 x / 1 – 3 tg 2 x
sin s cos t = (sin (s+t) + sin (s+t))/2
sin s sin t = (cos (s-t) – cos (s+t))/2
cos s cos t = (cos (s+t) + cos (s-t))/2
Формулы дифференцирования
x’ = 1 (sin x)’ = cos x
(kx + m)’ = k (cos x)’ = – sin x
(1/x)’ = – (1/x 2 ) ( ln x)’ = 1/x
(e x )’ = e x ; (x n )’ = nx n-1 ;(log a x)’=1/x ln a
Площади плоских фигур
1. Прямоугольный треугольник
S = 1/2 a·b (a, b – катеты)
2. Равнобедренный треугольник
S = (a/2)·√ b 2 – a 2 /4
3. Равносторонний треугольник
S = (a 2 /4)·√3 (a – сторона)
4. Произвольный треугольник
a,b,c – стороны, a – основание, h – высота, A,B,C – углы, лежащие против сторон; p = (a+b+c)/2
S = 1/2 a·h = 1/2 a 2 b sin C =
a 2 sinB sinC/2 sin A= √p(p-a)(p-b)(p-c)
a,b – стороны, α – один из углов; h – высота S = a·h = a·b·sin α
cos (x + π/2) = -sin x
Формулы tg и ctg
tg x = sin x/ cos x; ctg x = cos x/sin x
ctg (x + πk) = ctg x
ctg (x ± π) = ± ctg x
tg (x + π/2) = – ctg x
ctg (x + π/2) = – tg x
sin 2 x + cos 2 x =1
1 + tg 2 x = 1/ cos 2 x
1 + ctg 2 x = 1/ sin 2 x
tg 2 (x/2) = 1 – cos x/ 1 + cos x
cos 2 (x/2) = 1 + cos x/ 2
sin 2 (x/2) = 1 – cos x/ 2
P = 4 πR 2 = πD 2
V = πh 2 (R-1/3h) = πh/6(h 2 + 3r 2 )
SБОК = 2 πRh = π(r 2 + h 2 ); P= π(2r 2 + h 2 )
V = 1/6 πh 3 + 1/2 π(r 2 + h 2 )· h;
14. Шаровой сектор:
V = 2/3 πR 2 h’ где h’ – высота сегмента, содержащего в секторе
Формула корней квадратного уравнения
ax 2 + bx + c = 0 (a≠0)
Если D=0, то x = -b/2a (D = b 2 -4ac)
Если D>0, то x1,2 = -b± /2a
Арифметическая прогрессия
a n+1 = a n + d, где n – натуральное число
d – разность прогрессии;
a n = a 1 + (n – 1)·d – формула n-го члена
Радиус описанной окружности около многоугольника
R = a/ 2 sin 180/n
Радиус вписанной окружности
L = 2 πR S = πR 2
Площадь конуса
Тангенс угла - отношение противолежащего катета к прилещащему. Котангенс – наоборот.
Скачать шпаргалки по математике
Скачать всё это в компактном виде: matematika-shpory.doc.
Рекомендуем:
В 2020 году структура ОГЭ по математике претерпела некоторые изменения. Ниже рассмотрим эти изменения подробнее.
Справочные материалы (выдаются на экзамене каждому)
ОГЭ 2020 по математике состоит из двух частей.
- В первой части 20 заданий (1 – 20) базового уровня сложности, каждое из которых оценивается в 1 балл .
- Во второй части 6 заданий (21 – 26) повышенного и высокого уровня сложности, каждое из которых оценивается в 2 балла .
Всего за экзамен можно набрать 32 балла.
Время, которое отводится на экзамен – 235 минут .
Структура ОГЭ 2020 по математике: первая часть
Первая часть состоит из:
Ответом к каждому заданию первой части является число, цифра или последовательность цифр. Ответы на задания первой части проверяются компьютером.
Структура ОГЭ 2020 по математике: вторая часть
Вторая часть состоит из двух модулей:
Ответом к каждому заданию второй части является письменное решение, которое проверяется двумя независимыми экспертами. Они проставляют в протокол оценки за каждое задание второй части. В случае, если оценки двух экспертов расходятся, назначается третий.
Выставление оценок за работу
- Оценка за экзаменационную работу выставляется по следующим критериям:
| Количество баллов | Оценка |
| 0 – 7 | 2 |
| 8 – 14 | 3 |
| 15 – 21 | 4 |
| 22 – 32 | 5 |
- Оценка по алгебре выставляется по следующим критериям:
| Количество баллов за модуль алгебра | Оценка |
| 0 – 4 | 2 |
| 5 – 10 | 3 |
| 11 – 15 | 4 |
| 16 – 20 | 5 |
- Оценка по геометрии выставляется по следующим критериям:
| Количество баллов за модуль геометрия | Оценка |
| 0 – 2 | 2 |
| 3 – 4 | 3 |
| 5 – 7 | 4 |
| 8 – 12 | 5 |
Результаты ОГЭ, в частности, ОГЭ по математике, влияют на дальнейшую судьбу 9-классника:
- для кого-то баллы, набранные на ОГЭ, важны для поступления в профильный класс или лицей,
- для кого-то это возможность получить аттестат и поступить в техникум,
- для кого-то это возможность улучшить годовую оценку по предмету.
В любом случае, успешная сдача экзамена – необходимый шаг, который каждому нужно совершить в своей жизни.
И это несложно!

Видео-уроки на канале Ёжику Понятно. Подпишись!

В 2020 ОГЭ будет предполагать сдачу четырех экзаменов, два из которых являются обязательными (русский язык и математика), а два на усмотрение учащегося. Положительная сдача экзамена необходима для получения аттестата о получении основного общего образования. В данной статье мы рассмотрим структуру сдачи экзамена по математике, а также нововведения и полезные советы.
Дата проведения ОГЭ по математике 2020
Обращаем внимание, что это является не финальным расписанием, а лишь проектом, который может претерпеть изменения.
- 21 апреля (вторник) – математика;
- 12 мая (вторник) – математика;
- 16 мая (суббота) – по всем учебным предметам;
- 9 июня (вторник) – математика;
- 24 июня (среда) – математика;
- 25 июня (четверг) – по всем учебным предметам;
- 30 июня (вторник) – по всем учебным предметам;
- 10 сентября (четверг) – математика;
- 17 сентября (четверг) – математика;
- 21 сентября (понедельник) – по всем учебным предметам;
Как устроен экзамен ОГЭ по Математике
Задания КИМ 2020 года по математике претерпели изменения, однако формат остается прежним.
Итак, рассмотрим эти изменения:
- Добавлен новый вид заданий для ОГЭ по математике — с 1 по 5 номера. Необходимо ознакомиться с представленными рисунком и текстом в начале, на основе которых и выполняются задачи. Их нельзя назвать сложными, однако они требуют внимательности.
- Остальные номера соответствуют определенным задачам из прошлогодних КИМов, некоторые с незначительными изменениями.
Работа по математике состоит из двух частей, включающих в себя 26 заданий:
- В первой части 20 номеров (1 — 20) базового уровня сложности.
- Во второй части 6 номеров (21 — 26) повышенного и высокого уровня сложности.
К 1-20 заданиям ответ необходимо записать в виде цифр или числовой последовательности. К 21-26 — даётся развёрнутый ответ.
Всего за экзамен можно набрать 32 балла.
Время, которое отводится на экзамен — 235 минут.
На экзамене в каждом КИМе предоставляются справочные материалы по алгебре и геометрии, которые включают в себя следующие формулы:
- Формула корней квадратного уравнения;
- Формула разложения на множители квадратного трехчлена;
- Формула n -го члена арифметической прогрессии;
- Формула суммы первых n членов арифметической прогрессии;
- Формула n -го члена геометрической прогрессии;
- Формула суммы первых n членов геометрической прогрессии;
- Таблица квадратов двузначных чисел.
- Сумма углов выпуклого n -угольника;
- Радиус r окружности, вписанной в правильный треугольник;
- Радиус R окружности, описанной около правильного треугольника;
- Теорема синусов;
- Теорема косинусов;
- Формула длины l окружности;
- Формула длины l дуги окружности;
- Формула площади S параллелограмма;
- Формула площади S треугольника;
- Формула площади S трапеции.
Также можно и нужно использовать черновик. Все записи, сделанные на черновике, не рассматриваются при оценивании, поэтому можно смело записывать на листах все, что необходимо, и не бояться исправлять ошибки.
Баллы ОГЭ по математике
За успешное выполнение заданий по математике ОГЭ-2020 учащийся сможет получить 32 тестовых балла:
| Задания | Баллы |
| 1-20 | 1 |
| 21-26 | 2 |
Для перевода тестового балла ОГЭ по математике в пятибалльную отметку ФИПИ рекомендует пользоваться следующей таблицей соответствия:
| Тестовый балл | Отметка |
| 0-7 | “2” (не сдал) |
| 8-14 | “3” |
| 15-21 | “4” |
| 22-32 | “5” |
Важно! Для прохождения аттестационного порога необходимо набрать не менее 8 баллов, из которых не менее 2 баллов должны быть получены за решение заданий по геометрии (номера 16–20, 24–26).
Как готовиться и на что обратить внимание
Все задания КИМа разделяются на два модуля:
- Алгебра — 14 номеров в первой части и 3 — во второй части.
- Геометрия — 6 номеров в первой части и 3 — во второй части.
Если говорить о подготовке к математике с нуля, то сразу же смотрим, на какие темы разбиваются модули.
- Базовые темы
- Уравнения
- Неравенства
- Текстовые задачи
- Тригонометрия
- Функции и графики
- Продвинутая теория
- Планиметрия
- Стереометрия
Разумеется, подготовка должна быть выстроена “от простого к сложному”, т.к. без знания, например, темы “биссектриса”, вы не сможете решить многие более сложные задачи.
Для самостоятельного изучения теории математики вы можете использовать школьные учебники и интернет-ресурсы. Для решения заданий из КИМов рекомендуем сборники под редакцией Ф.Ф. Лысенко. Если вы понимаете, что необходимо обратиться к специалисту, то всегда можете заручиться поддержкой школьного учителя, либо взять уроки у репетитора или онлайн-занятия. В последнем случае вы не ограничены местом жительства, временем и дорогой. Под руководством компетентных специалистов вы сможете освоить не только азы этой науки, но и получить более углубленные знания, полезные советы и хитрости подготовки и сдачи экзамена.
Обязательно заведите тетрадь, в которой будете конспектировать всю полезную информацию: формулы, доказательства, признаки, свойства и т.д.
Теорию необходимо сразу же закреплять практикой путем прорешивания вариантов ОГЭ из сборников, которые представлены в виде тематических и типовых. В тематических для каждой темы подобраны все виды заданий по ОГЭ, а в типовых — варианты представлены в том виде, в котором они будут на экзаменах. Начать подготовку лучше с тематических сборников.
Советы по подготовке к ОГЭ по Математике
Какой бы способ обучения вы не выбрали – самостоятельно или с репетитором – советы по подготовке будут полезными.
Теория нужна и важна.
Без основательного знания теоретических основ невозможно перейти к практике и, соответственно, к решению заданий ОГЭ.
Не спешите переходить сразу к сложным задачам КИМа, начните с более простых вопросов, которые, по сути своей, служат базовыми знаниями.
Практика.
Владение теорией, безусловно, важный пункт, но не забывайте практиковаться: решение практических заданий поможет не только лучше понять тему, но и закрепит полученные знания.
Не забывайте про формулы.
Без знания формул невозможно решение многих заданий, поэтому обязательно законспектируйте необходимые формулы и впоследствии выучите их.
Официальные шпаргалки.
Вместе с КИМами на экзамене выдаются справочные материалы (см. выше). Если научиться правильно ими пользоваться, то не придется запоминать абсолютно все формулы.
Видео лекций и вебинаров.
В интернете существует большое количество видеороликов, посвященных разбору каждого типа заданий КИМа. Вы можете выбрать лектора, язык которого наиболее доступен лично для вас.
Не забывайте о времени.
При решении полных вариантов КИМов обращайте внимание на время, ведь время экзамена ограничено, и важно уметь его правильно распределять.
Проверяйте.
Обязательно проверяйте все действия, в т.ч. вычислительные, а также соответствие вашего решения или ответа условиям задач, т.к. из-за невнимательности можно потерять баллы. Также их можно потерять за неполный ответ.
На какие задания обратить внимание
Задания 1-5. Несмотря на простоту номеров, многие школьники совершают в них ошибки из-за невнимательности. Обязательно читайте условия задач, чтобы не пропустить важные факты. Если необходимо, выписывайте все на черновик, чертите на рисунках в КИМах.
Задание 11. Установление соответствия между графиками функций и формулами, которые их задают. Часто учащиеся просто пытаются наугад подставить цифры. Однако тут всего лишь нужно немного поразмыслить логически. Попробуйте подставить значения x и y.
Задание 13. Задача прикладного содержания. Из несложной формулы необходимо выразить одну из величин, найти ее значение, а ответ записать в указанных единицах измерения. Сложность здесь как раз заключается в переходе от одной размерности к другой.
Задание 21. При решении алгебраических уравнений или неравенств обязательно обращайте внимание на все решения. Очень часто ученик либо теряет решение, либо, наоборот, получает постороннее решение. Оба варианта лишают 1-2 баллов. Также не стоит забывать, что при умножении неравенства на отрицательное число, знак неравенства меняется.
Задание 22. Как правило, у большого количества школьников данная задача вызывает затруднение. В качестве обязательного совета — делайте и заполняйте таблицу известными величинами и переменными. Это позволит вам иначе взглянуть на задание и составить необходимые уравнения.
Задание 23. Построение графика функции. Для выполнения этого номера нужно знать свойства функций (линейная, квадратичная, либо функция, описывающая обратно пропорциональную зависимость). Также необходимо практиковаться в правильном построении графиков этих функций и ознакомиться с правилами преобразования графиков. Зачастую попадаются задания, в которых формулу исходной функции можно преобразовать, что значительно упрощает её. Однако здесь необходимо помнить, что область определения исходной и получившейся функции могут не совпадать.
Задание 26. Этот номер заслуженно один из самых сложных в экзамене по математике, т.к. требует широкого спектра знаний. С большой долей вероятности потребуются дополнительные построение, знание утверждений, которые практически не используются в школьном курсе, и, конечно, умение выражать свои мысли математически грамотно.
Читайте также:


