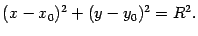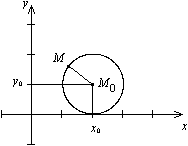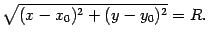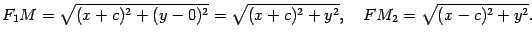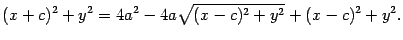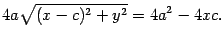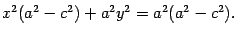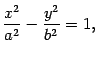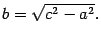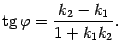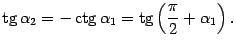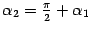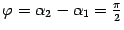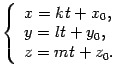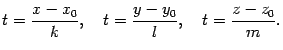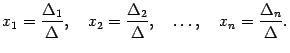Алгебра и геометрия шпоры 1 курс 1 семестр
Шпаргалки по математике, алгебре и геометрии Шпаргалки по физике / Шпаргалки по химии
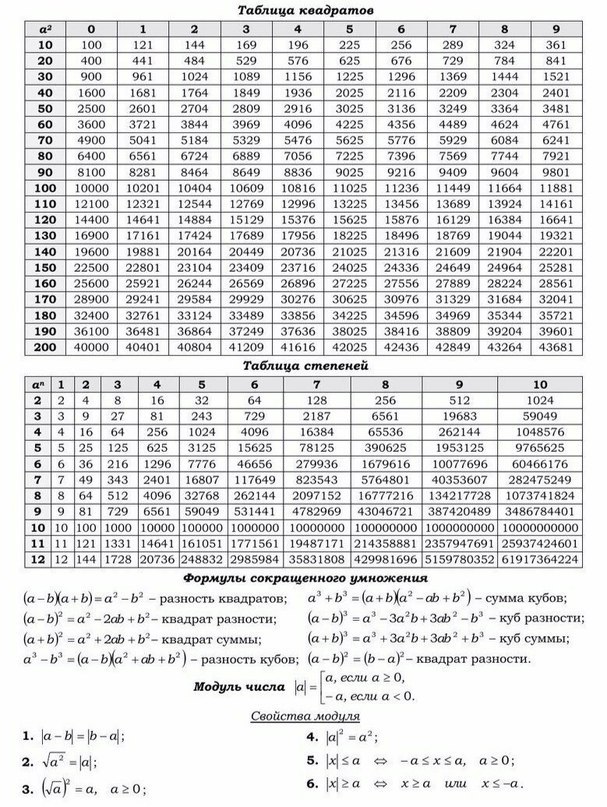
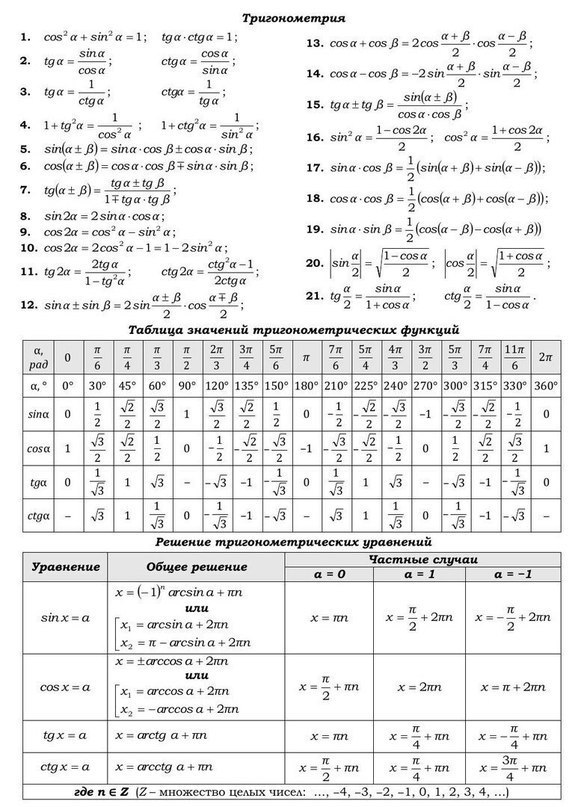
| Таблица квадратов. Таблица степеней. Формулы сокращенного умножения. Модуль числа. Свойства модуля: | Уравнения и неравенства с модулем. Последовательности и прогрессии. Метод кординат на плоскости. Скалярное произведение векторов. Расстояние между точками. | Тригонометрия - основные формулы. Таблица значений тригонометрических функций. Решение тригонометрических уравнений: | Четность и нечетность тригонометрических функций. Обратные тригонометрические функции. Формулы приведения. Знаки тригонометрических функций. Показательные уравнения и неравенства. |
 |  |  |  |
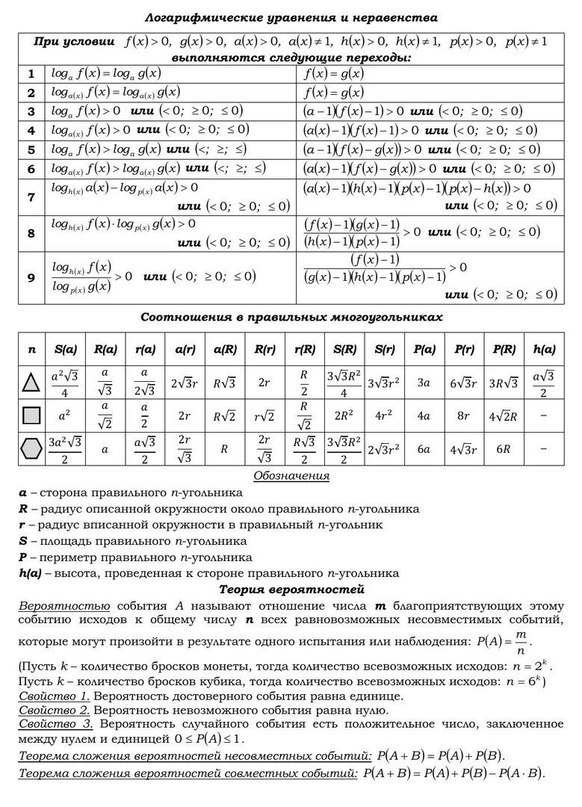
| Корень n-ой степени. Степени. Иррациональные уравнения и неравенства. Логарифм, свойства логарифмов | Логарифмические уравнения и неравенства. Соотношения в правильных многоугольниках. Теория вероятностей. Теоремы сложения вероятностей. | Логарифмические уравнения и неравенства. | Производная. Правила дифференцирования. Производная сложной функции. Уравнение касательной к графику функции в точке. |
 |  |  |  |
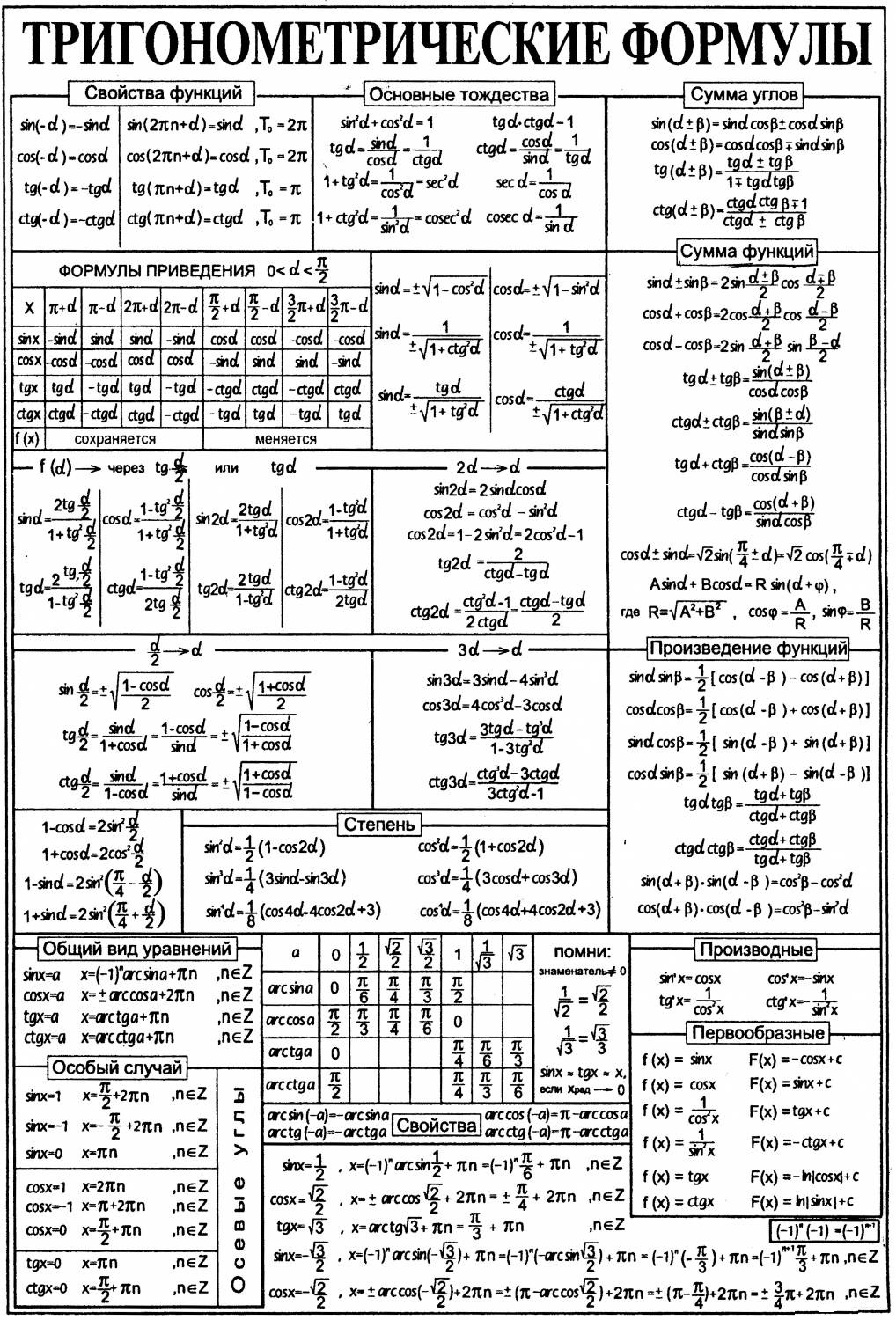
| Тригонометрические формулы. Свойства функций, основные тождества, сумма углов. Сумма функций, формулы приведения, особые случаи, степени, половинные, двойные и тройные углы. Обратные функции. | |||
 |
| Набор 2 - Алгебра. Линейная алгебра. | |||
| Свойства степеней. Формулы сокращенного умножения. Свойства арифметических корней. Модуль. Начала математического анализа: прогрессии арифметическая и геометрическая. Производная. Первообразная и интеграл. Среднее арифметическое и среднее геометрическое. | Тригонометрия. Основные формулы. Арксинус, арккосинус, арктангенс, арккотангенс. Четность функций. Значения тригонометрических функций некоторых углов. | Графики некоторых элементарных функций. Логарифмы. Решение квадратных, иррациональных, показательных, тригонометрических уравнений, уравнений с модулем | Квадратные неравенства. Неравенства с модулем. Логарифмические неравенства. Неравенства с модулем. Иррациональные неравенства. Показательные неравенства. Комбинаторика и бином Ньютона. |
 |  |  |  |
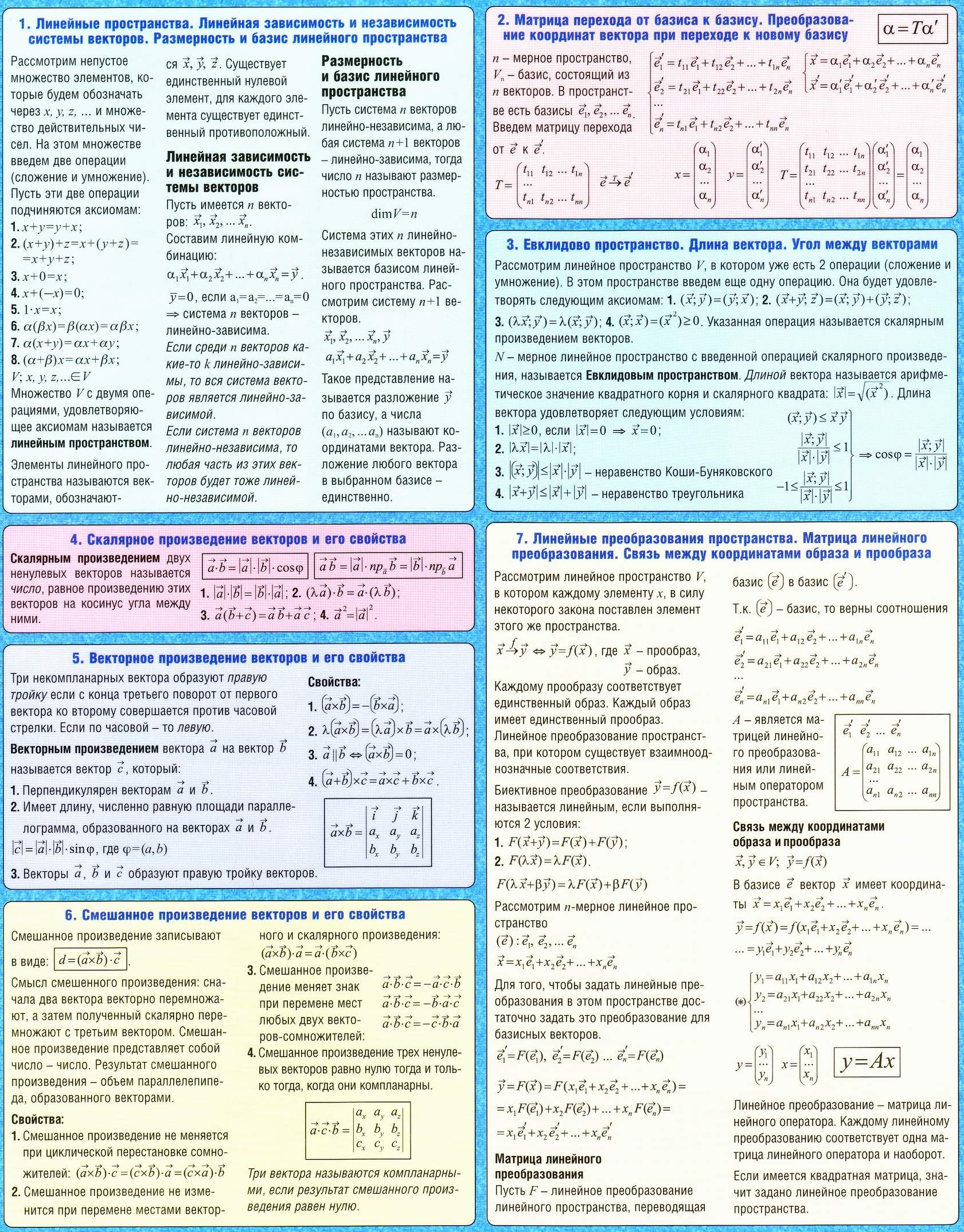
| Определение комплексного числа. Геометрическая интерпретация комплексного числа. Тригонометрическая форма комплексного числа. Показательная форма комплексного числа. Действия с комплексными числами. Последовательности, пределы последовательности. Теоремы о пределах числовых последовательностей. | Определение предела числовой функции. Односторонние пределы. Свойства пределов. Непрерывные функции и их свойства. Точки разрыва и их классификации. Замечательные пределы. Важные пределы. Теоремы о среднем. Правило Лопиталя. | Линейные пространства. Линейная зависимость и независимость системы векторов. Размерность и базис линейного пространства. Скалярное и векторное произведение векторов. Смешанное произведение векторов. Матрица перехода от базиса к базису. Преобразование координат вектора при переходе к новому базису. Евклидово пространство. Длина вектора. Угол между векторами. Линейные преобразования пространства. Матрица линейного преобразования. Связь между координатами образа и прообраза. | Связь между координатами одного и того же линейного оператора в разных базисах. Угол между прямой и плоскостью. Расстояние от точки до плоскости. Характеристические уравнения линейного оператора. Собственные векторы линейного оператора и их свтойства. Поверхности второго порядка. Плоскость в пространстве. Виды углов в пространстве. Уравнения плоскости. |
 |  |  |  |
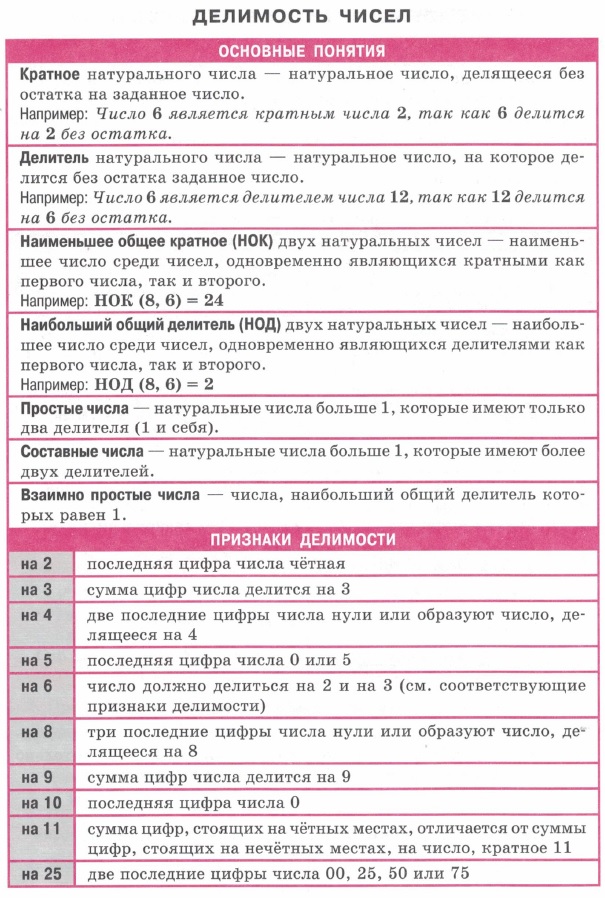
| Делимость чисел. Кратное. Делитель. НОК. НОД Простые и составные числа. Взаимно простые числа. | Числовые последовательности, члены, способы задания. Арифметическая и геометрическая прогрессии. Формулы. Характеристические свойства | Числа. Множества натуральных, целых, рациональных, действительных, иррациональных чисел. Арифметические действия с дробями. Модуль - свойства. | Решение квадратных уравнений. Формулы дискриминанта. Решение неполных квадратных уравнений. Теорема Виета. Алгоритм решения квадратного неравенства. |
 |  |  |  |
| Основные свойства функций. Понятие функции. Четность и нечетность. Периодичность. Нули функции. Промежутки знакопостоянства. Монотонность (возрастание, убывание). Асимптоты. Алгоритм описания фукнкции. |
Преобразование графиков функций у= f(x) в y=-f(x); y=f(-x); y=-f(-x); y=f(x-a); y=f(x)+b; y=f(ax); y=kf(x); y=|f(x)|; y=f(|x|). Построение графика обратной функции Степенные функции y=xn и y=x1/n, n∈Z. Свойства, графики. Квадратичная функция. Свойства степеней. Свойства арифметических корней. Формулы сокращенного умножения. Примеры значения степенных функций. Неравенства, понятия, строгие, нестрогие, решение. Свойства неравенств. Решение линейных неравенств. Решение квадратных неравенств. Метод интервалов при решении неравенств. Решение показательных неравенств. Решение логарифмическмх неравенств. Решение иррациональных неравенств. Решение неравенств с модулем. Часто применяемые неравенства Интегрирование функций. Понятие и основное свойство первообразной. Неопределенный интеграл. Правила интегрирования. Определенный интеграл. Формула Ньютона-Лейбница. Свойства и геометрический смысл определенного интеграла. Физический смысл определенного интеграла Уравнения прямой на плоскости. Общее уравнение прямой. Уравнение прямой "в отрезках". Уравнение прямой с угловым коэффициентом. Уравнение пучка прямых, проходящих через точку. Уравнение прямой, проходящей через 2 точки. Нормальное уранение прямой. Консультации и техническая Лектор проф. А.Л.Городенцев, преподаватели доц. Н.С.Маркарян, доц. Йен Маршалл Помимо записок лекций, которые мало-помалу будут появляться ниже, для подготовки к экзаменам и выполнения контрольных работ рекомендуются следующие учебники: Записки лекций
Задачи семинаров Листок 1: векторы, точки и прямые на координатной плоскости. Выдаётся с 1 сентября. Листок 2: увеличиваем размерность. Выдаётся с 20 сентября. Листок 3: примеры векторных пространств и базисов. Выдаётся с 28 сентября. Листок 4 Евклидова геометрия (выдается с 7 октября) Листок 5: аффинные и ортогональные преобразования. Выдаётся с 20 октября Контрольная работа № 1: евклидова геометрия в R 2 и в R 3 . Состоялась 27 сентября. Контрольную можно доделать дома и сдать 28 сентября перед семинаром по геометрии. Решения, сданные 28 сентября, оцениваются с весом 80% от номинала . Домашняя контрольная работа N2: евклидова геометрия в R 3 и в R 4 . Выдана 8 ноября. Номер Вашего варианта — это Ваш порядковый номер в алфавитном списке всех студентов 1-го курса (см., к примеру, список с результатами коллоквиума). Работу необходимо сдать 15 ноября перед занятием по геометрии . Домашняя контрольная работа N3: линейная оптимизация. Выдана 20 декабря. Номер Вашего варианта — тот же, что и в предыдущей контрольной (если он превышал 50, свяжитесь со мною лично). Работу необходимо сдать 27 декабря перед зачётом по геометрии .
По этому курсу происходят письменный зачёт (после 2-го модуля) и письменный экзамен (после 3-го модуля) и, соответственно, ставятся 2 итоговых отметки в зачётку (полсле 2-го и после 3-го модуля). Правила рассчёта итоговой отметки таковы. В каждом из 4-х видов деятельности — решение задач из листков, решение задач из контрольных, ответы на коллоквиумах, решение задач из зачётной (соотв. экзаменационной) работы — вычисляется процентная доля выполненных заданий от общего суммарного количества заданий дававшихся в этом виде деятельности за оцениваемый период (первые 2 модуля и 3-й модуль соответственно). Например, если за весь третий модуль Вы суммарно вы решили 30 задач из листков, а всего в третьем модуле было задано 100 задач без звёздочек, то Вы набираете за листки 30%. Пусть Вы успешно решили L% задач из листков, K% задач из контрольных, E% задач из экзаменционной (или зачётной) работы и справились с C% заданий коллоквиума. Максимальная оценка 10 баллов ставится во II модуле за L+K+E+C≥300, в III модуле — за L+K+E≥225 . При наборе меньшей суммы оценка уменьшается линейно. Письменный зачёт по материалам 1-го и 2-го модулей был 27 декабря. Вариант задания: (104 kB, PDF). Итоговый письменный экзамен по курсу геометрии был 27 марта. Вариант задания: (57 kB, PDF). Лектор проф. А.Л.Городенцев, преподаватели доц. Н.С.Маркарян, доц. Йен Маршалл Помимо записок лекций, которые мало-помалу будут появляться ниже, для подготовки к экзаменам и выполнения контрольных работ рекомендуются следующие учебники: Записки лекций
Задачи семинаров Листок 1: векторы, точки и прямые на координатной плоскости. Выдаётся с 1 сентября. Листок 2: увеличиваем размерность. Выдаётся с 20 сентября. Листок 3: примеры векторных пространств и базисов. Выдаётся с 28 сентября. Листок 4 Евклидова геометрия (выдается с 7 октября) Листок 5: аффинные и ортогональные преобразования. Выдаётся с 20 октября Контрольная работа № 1: евклидова геометрия в R 2 и в R 3 . Состоялась 27 сентября. Контрольную можно доделать дома и сдать 28 сентября перед семинаром по геометрии. Решения, сданные 28 сентября, оцениваются с весом 80% от номинала . Домашняя контрольная работа N2: евклидова геометрия в R 3 и в R 4 . Выдана 8 ноября. Номер Вашего варианта — это Ваш порядковый номер в алфавитном списке всех студентов 1-го курса (см., к примеру, список с результатами коллоквиума). Работу необходимо сдать 15 ноября перед занятием по геометрии . Домашняя контрольная работа N3: линейная оптимизация. Выдана 20 декабря. Номер Вашего варианта — тот же, что и в предыдущей контрольной (если он превышал 50, свяжитесь со мною лично). Работу необходимо сдать 27 декабря перед зачётом по геометрии .
По этому курсу происходят письменный зачёт (после 2-го модуля) и письменный экзамен (после 3-го модуля) и, соответственно, ставятся 2 итоговых отметки в зачётку (полсле 2-го и после 3-го модуля). Правила рассчёта итоговой отметки таковы. В каждом из 4-х видов деятельности — решение задач из листков, решение задач из контрольных, ответы на коллоквиумах, решение задач из зачётной (соотв. экзаменационной) работы — вычисляется процентная доля выполненных заданий от общего суммарного количества заданий дававшихся в этом виде деятельности за оцениваемый период (первые 2 модуля и 3-й модуль соответственно). Например, если за весь третий модуль Вы суммарно вы решили 30 задач из листков, а всего в третьем модуле было задано 100 задач без звёздочек, то Вы набираете за листки 30%. Пусть Вы успешно решили L% задач из листков, K% задач из контрольных, E% задач из экзаменционной (или зачётной) работы и справились с C% заданий коллоквиума. Максимальная оценка 10 баллов ставится во II модуле за L+K+E+C≥300, в III модуле — за L+K+E≥225 . При наборе меньшей суммы оценка уменьшается линейно. Письменный зачёт по материалам 1-го и 2-го модулей был 27 декабря. Вариант задания: (104 kB, PDF). Итоговый письменный экзамен по курсу геометрии был 27 марта. Вариант задания: (57 kB, PDF). Окружность радиуса R с центром в точке M0(x0, y0) имеет уравнение
Доказательство. Пусть M(x,y) -- текущая точка окружности. По определению окружности расстояние MM0 равно R:
По формуле скалярного произведения для плоскости получаем, что точки окружности и только они удовлетворяют уравнению
Обе части уравнения неотрицательны. Поэтому после возведения их в квадрат получим эквивалентное уравнение. Если в уравнении (12.2) раскрыть скобки и привести подобные члены, то вид его изменится. Однако любое уравнение окружности с помощью тождественных преобразований можно привести к виду (12.2). Для этого достаточно выделить полные квадраты по переменным X и Y. Пусть сумма расстояний от точки эллипса до фокусов равна 2a, а расстояние между фокусами – 2c . Тогда в выбранной системе координат эллипс имеет уравнение
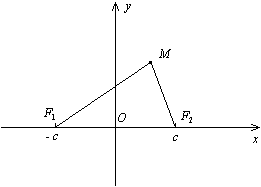
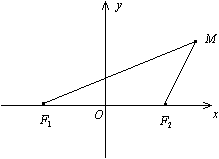
Доказательство. Пусть M(x,y) -- текущая точка эллипса. По определению эллипса F1M+F2M=2a . Из треугольника F1MF2 (рис. 12.3) видно, что F1M+F2M > F1F2 , то есть 2a>2c, a>c, и поэтому число b=sqrt(a^2 - b&2) существует.
Фокусами в выбранной системе координат являются точки F1(-c,0) , F2(c,0). По формуле (10.4) для плоского случая находим
Тогда по определению эллипса
Пренесем один из корней вправо и обе части возведем в квадрат:
После того, как раскроем скобки и приведем подобные члены, приходим к выражению
Разделим обе части этого уравнения на 4 и возведем в квадрат
Раскроем скобку и приведем подобные члены
Учитывая, что b^2= a^2 - c^2, имеем равенство
Наконец, разделив обе части на (a^2)(b^2) , получим исходное уравнение (12.4). Пусть расстояние между фокусами F1 и F2 гиперболы равно 2c , а абсолютная величина разности расстояний от точки гиперболы до фокусов равна 2a . Тогда гипербола в выбранной выше системе координат имеет уравнение
Доказательство. Пусть M(x,y) -- текущая точка гиперболы (рис. 12.9).
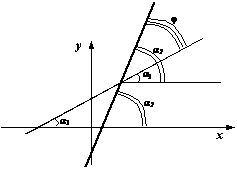
Так как разность двух сторон треугольника меньше третьей стороны, то |F1M – F2M| k1). Тогда, если k1*k2!=-1 , то угол fi между этими прямыми можно найти из формулы
Если k1*k2=-1 , то прямые перпендикулярны Доказательство. Как известно из школьного курса математики, угловой коэффициент в уравнении прямой y=kx+b равен тангенсу угла alfa наклона прямой к оси Ox . Из рис. 11.10 видно, что fi=alfa2-alfa1 .
Так как tg(alfa1)=k1 , tg(alfa2)=k2 , то при k2*k1!=-1 выполняется равенство
что и дает исходную формулу. Если же k1*k2=-1, то tg(alfa1)*tg(alfa2)=-1, откуда
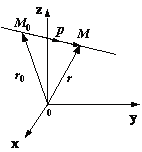
Каноническое уравнение прямой в пространстве. Ненулевой вектор, лежащий на прямой (параллельный ей) называется направляющим вектором прямой Пусть для прямой Y известны ее направляющий вектор p=(k,l,m) и точка M0(x0,y0,z0) , лежащая на этой прямой. Пусть M(x,y,z) -- произвольная (текущая) точка прямой Y . Обозначим через r0 и r радиус-векторы точек M0 и M соответственно (рис. 11.11).
Тогда вектор M0M коллинеарен вектору p и, следовательно, M0M=tp , где t -- некоторое число. Из рис. 11.11 видно, что Это уравнение называется векторным уравнением прямой или уравнением в векторной форме. От векторного соотношения перейдем к соотношениям координат. Так как (x,y,z) -- координаты точки M , то r=(x,y,z) , r0=(x0,y0,z0) , tp=(tk,tl,tm) . Из формулы (11.12) получим
Полученная система уравнений называется параметрическими уравнениями прямой. Выразим параметр t:
Так как во всех трех соотношениях параметр t имеет одно и то же значение, то
Эти уравнения называются каноническими1 уравнениями прямой. Правило Крамера: Если в системе n линейных уравнений с n неизвестными delta !=0 , то система имеет решение и притом единственное. Это решение задается формулами
где A(ij) -- алгебраические дополнения. Тогда из (15.3) следует, что
Заметим, что по формуле (14.13) разложение определителя delta1 по первому столбцу в точности совпадает с первым элементом матрицы-столбца в правой части последнего равенства, разложение определителя delta2 по второму столбцу дает второй элемент матрицы-столбца и т.д. Поэтому: Система линейных уравнений (15.1) является совместной тогда и только тогда, когда ранг матрицы системы A равен рангу расширенной матрицы A* .
Доказательство. Оно распадается на два этапа. Пусть система имеет решение. Покажем, что RgA=RgA* Пусть набор чисел (a1,a2. an) является решением системы. Обозначим через a(i) i -ый столбец матрицы A , i=1,2…n . Тогда a1a1+ a2a2+…+anan=b, то есть столбец свободных членов является линейной комбинацией столбцов матрицы A . Пусть r=RgA . Предположим, что RgA*!=RgA . Тогда по предложению 15.1 RgA*=r+1 . Выберем в A* базисный минор M . Он имеет порядок r+1 . Столбец b свободных членов обязан проходить через этот минор, иначе он будет базисным минором матрицы A . Столбец свободных членов в миноре M является линейной комбинацией столбцов матрицы A . В силу свойств определителя ( предложения 14.13, 14.18) M=a1M1+a2M2+…+anMn , где M(i) -- определитель, который получается из минора M заменой столбца свободных членов на столбец a(i) . Если столбец a(i) проходил через минор M , то в M(i) , будет два одинаковых столбца и, следовательно,M(i)=0 . Если столбец a(i) не проходил через минор M , то M(i) будет отличаться от минора порядка r+1 матрицы A только порядком столбцов. Так как RgA=r , то M(i)=0 . Таким образом,M=a1*0+a2*0+…+an*0=0 , что противоречит определению базисного минора. Значит, предположение, что RgA*!=RgA , неверно. 2. Пусть RgA=RgA* . Покажем, что система имеет решение. Так как RgA=RgA* , то базисный минор M матрицы A является базисным минором матрицы A* . Пусть через минор M проходят столбцы a(i1),a(i2),…,a(ir) . Тогда по теореме о базисном миноре в матрице A* столбец свободных членов является линейной комбинацией указанных столбцов:
Положим x
В силу равенства (15.6) x<1>a<1>+x<2>a<2>+…+x При элементарных преобразованиях ранг матрицы не меняется Доказательство. Пусть ранг матрицы A равен r , A’ -- матрица, получившаяся в результате выполнения элементарного преобразования. Рассмотрим перестановку строк. Пусть M -- минор матрицы A , тогда в матрице A’ есть минор M’ , который или совпадает с M , или отличается от него перестановкой строк. И наоборот, любому минору N’ матрицы A’ можно сопоставить минор матрицы A или совпадающий с N’ , или отличающийся от него порядком строк. Поэтому из того, что в матрице A все миноры порядка r+1 равны нулю, следует, что в матрице A’ тоже все миноры этого порядка равны нулю. И так как в матрице A есть минор порядка r , отличный от нуля, то и в матрице A’ тоже есть минор порядка r , отличный от нуля, то есть RgA’=r . Рассмотрим умножение строки на число a , отличное от нуля. Минору M из матрицы A соответствует минор M’ из матрицы A’ или совпадающий с M , или отличающийся от него только одной строкой, которая получается из строки минора M умножением на число, отличное от нуля. В последнем случае M’=aM . Во всех случаях или M и M’ одновременно равны нулю, или одновременно отличны от нуля. Следовательно, RgA’=r . Пусть к i-ой строке матрицы A прибавлена ее j-ая строка, умноженная на число lamda . Рассмотрим миноры порядка r+1 в матрице A’ . Если через минор M’ не проходит i-ая строка, то он совпадает с минором M , расположенным в тех же строках и столбцах в матрице A , и следовательно, равен нулю. Если через минор M’ проходят и i-ая и j-ая строки, то он получается из минора M , расположенного в тех же строках и столбцах матрицы A , прибавлением к i-ой строке минора M j-ой строки, умноженной на lamda . По свойству определителя M=M’ . Следовательно, M’=0 . Пусть через минор M’ проходит i-ая строка и не проходит j-ая. Тогда M’ отличается от M i-ой строкой. Эта строка в M’ является строкой M , к которой добавлены элементы j-ой строки, умноженные на lamda . По свойствам определителей M’=M+lamda(+-N) , где N -- минор порядка r+1 матрицы A , стоящий в j-ой строке и в тех же строках, что и минор M , исключая i-ую, а знак " +-" связан с возможным изменением порядка строк. Так как все миноры порядка r+1 в матрице A равны нулю, то M’=0 . Итак, в матрице A’ все миноры порядка r+1 равны нулю. Следовательно, RgA’ Соседние файлы в предмете Алгебра и геометрия
Читайте также:
| ||