Что такое капиллярные мениск

Рис. 1.10. Капиллярное впитывание жидкости: а — вертикальный капилляр; 6 — горизонтальный капилляр

Для капиллярного впитывания (рис. 1.10) важной характеристикой является его скорость v, определяемая капиллярным давлением и вязким сопротивлением течению жидкости в капилляре.

Скорость v перемещения мениска в горизонтально расположенном капилляре (или в очень тонком вертикальном капилляре, когда влияние силы тяжести мало) определяется уравнением Пуазейля

где Ар = -2а/г - разность давлений на нижнем и верхнем уровнях столба жидкости в капилляре.

В общем случае, т.е. с учетом изменения составляющей силы тяжести с ростом столба жидкости в капилляре, скорость v для вертикально расположенного капилляра (рис. 1.10, а) изменяется со временем впитывания / в соответствии с соотношением

где г_к - радиус капилляра; г| - коэффициент вязкости жидкости; И(1) — положение мениска в момент времени /; р — плотность жидкости в капилляре.

При впитывании жидкости в горизонтальный капилляр (рис. 1.10, б) соотношение (1.10) преобразуется к виду

Пример 1.4. Определить высоту /г_ж столбика жидкости, которая может удержаться в трубке, если ее полностью заполнить в горизонтальном положении, а затем повернуть вертикально. Диаметр и высота капиллярной трубки равны соответственно и П_к. Краевой угол смачивания равен 0.

Решение. Из баланса давлений вследствие кривизны свободных поверхностей жидкости в капилляре (а их, как указывалось выше, две) и гидростатического давления столба жидкости И_ж находим решение.

Согласно соотношению (1.6) и с учетом вышесказанного

Рис. 1.11. Передвижение жидкости в капилляре переменного сечения

Капиллярное передвижение жидкости может вызывать и градиент капиллярного давления, возникающий в результате различия кривизны поверхностей менисков жидкостного образования в капилляре переменного сечения (рис. 1.11). Для смачивающих жидкостей поток жидкости направлен к мениску с меньшим радиусом кривизны (т.е. в сторону меньшего давления).

Причиной капиллярного передвижения может быть не только градиент кривизны мениска, но и градиент поверхностного натяжения жидкости.

Так, градиент температуры приводит к разности значений поверхностного натяжения и соответственно разности значений капиллярного давления в жидкости (термокапиллярное течение). Этим же объясняется движение капель жидкости и пузырьков газа в неравномерно нагретой среде: под влиянием градиента поверхностного натяжения приходит в движение поверхность пузырьков или капель.

Аналогичный эффект наблюдается и при изменении поверхностного натяжения при адсорбции поверхностно-активных веществ (ПАВ). Они снижают эластичность свободной поверхности жидкости и соответственно ее поверхностное натяжение. Жидкость перемещается в том направлении, где адсорбция ПАВ на ее поверхности меньше (эффект Маранго- ни — Гиббса).

Задачи для самостоятельного решения

• 1.1. Определить плотности воды и нефти при температуре 4°С, если известно, что 10 л воды при этой температуре имеют массу 10 кг, а масса того же объема нефти равна 8,2 кг. Сравнить плотность нефти с плотностью воды.
• 1.2. Цистерна заполнена нефтью плотностью 850 кг/м 3 . Диаметр цистерны 3 м, длина 6 м. Определить массу жидкости в цистерне.
• 1.3. Найти плотность смеси жидкостей, имеющей следующий массовый состав: керосин — 30%, мазут — 70%, если плотность керосина 790 кг/м 3 , а мазута 900 кг/м 3 .
• 1.4. Плотность нефти при температуре 15 °С равна 900 кг/м 3 . Диаметр резервуара 10 м. Нефть заполняет резервуар при этой температуре до высоты 12 м. Коэффициент теплового объемного расширения нефти 6,4 10

4 /град '. Расширение резервуара не учитывать. Определить, насколько поднимется уровень нефти в цилиндрическом резервуаре при увеличении температуры от 15 до 40 °С.

где коэффициенты В и b для данной жидкости имеют постоянное значение и определяются экспериментально. Установлено, что при температуре Г, = 15 °С динамический коэффициент вязкости нефти р, = 0,187 кгДм е), а при температуре Г, = 30 °С р, = 0,0312 кг/(м с). Определить постоянные В и b и вычислить значение р для нефти при температуре 1 = 25 °С.

• 1.9. Вода поступает в насос по всасывающей трубе, работающей под вакуумом. Минимальное абсолютное давление перед входом в насос р- 4 кПа. Температура перекачиваемой воды поднялась до 30 °С. Будет ли наблюдаться в этом случае явление кипения?
• 1.10. Для определения давления насыщенных паров жидкости используются две предварительно заполненные ртутью баромстриче-

Рис. 1. 12. Использование барометрических трубок для измерения давления

скис трубки (рис. 1.12). Одна из них служит барометром, а в другую с помощью пипетки по капле вводят испытываемую жидкость. Безвоздушное пространство над ртутью вскоре заполняется наряду с парами ртути также парами жидкости, а над мениском ртути образуется небольшой слой жидкости высотой Ah. Мениск ртути при этом понизится на величину, соответствующую давлению насыщенных паров жидкости. При температуре опытов 20 °С плотность воды 998,2 кг/м а плотность ртути 13 550 кг/м 3 . Определить давление насыщенных паров воды, если /( = 713 мм, Ah = 200 мм, показание барометра Н = 745 мм рт. ст.

• 1.11. Масса 100 капель спирта, вытекающего из капилляра, равна 0,71 г. Плотность спирта принять равной 0,9 г/см 3 . Определить поверхностное натяжение спирта, если диаметр шейки капли в момент отрыва равен 1 мм.
• 1.12. Глицерин плотностью 1.26 г/см 3 поднялся в капиллярной трубке внутренним диаметром 1 мм на высоту 20 мм. Определить коэффициент поверхностного натяжения глицерина.
• 1.13. Диаметр мыльного пузыря равен 5 мм. Определить, насколько давление воздуха внутри мыльного пузыря больше атмосферного давления. Поверхностное натяжение глицерина принять равным 0,061 Н/м.
• 1.14. В воду опущена на очень малую глубину стеклянная трубка, диаметр внутреннего канала которой равен 1 мм. Найти массу вошедшей в трубку воды. Поверхностное натяжение воды на границе с воздухом принять равным 0,07 Н/м.

Введение

В наш век высоких технологий все большее значение в жизни людей имеют естественные науки. Люди 21 века производят супер производительные компьютеры,смартфоны,все глубже и глубже изучают окружающий нас мир. Я думаю, что люди готовятся к новой научно технической революции, которая изменит наше будущее коренным образом. Но когда произойдут эти изменения никто не знает. Каждый человек своим трудом может приблизить этот день.

Эта научно-исследовательская работа – мой маленький вклад в развитие физики.

Цель исследовательской работы: обосновать с точки зрения физики причину движения жидкости по капиллярам, выявить особенности капиллярных явлений.

Объект исследования: свойство жидкостей, всасываясь, подниматься или опускаться по капиллярам.

Предмет исследования: капиллярные явления в живой и неживой природе.

1. Изучить теоретический материал о свойствах жидкости.
2. Ознакомиться с материалом о капиллярных явлениях.
3. Провести серию экспериментов с целью выяснения причины поднятия жидкости в капиллярах.
4. Обобщить изученный в ходе работы материал и сформулировать вывод.

Прежде чем перейти к изучению капиллярных явлений, надо ознакомиться со свойствами жидкости, которые играют немалую роль в капиллярных явлениях.

Поверхностное натяжение

Внутреннее давление обуславливает втягивание молекул, расположенных на поверхности жидкости, внутрь и тем самым стремится уменьшить поверхность до минимальной при данных условиях. Сила, действующая на единицу длины границы раздела, обуславливающая сокращение поверхности жидкости, называется силой поверхностного натяжения или просто поверхностным натяжением σ .

Поверхностное натяжение различных жидкостей неодинаково, оно зависит от их мольного объёма, полярности молекул, способности молекул к образованию водородной связи между собой и др.

При увеличении температуры поверхностное натяжение уменьшается по линейному закону. На поверхностное натяжение жидкости оказывают влияние и находящиеся в ней примеси. Вещества, ослабляющие поверхностное натяжение, называют поверхностно-активными (ПАВ). По отношению к воде ПАВ являются нефтепродукты, спирты, эфир, мыло и др. жидкие и твёрдые вещества. Некоторые вещества увеличивают поверхностное натяжение. Примеси солей и сахара, например.

Объяснение этому даёт МКТ. Если силы притяжения между молекулами самой жидкости больше сил притяжения между молекулами ПАВ и жидкости, то молекулы жидкости уходят внутрь из поверхностного слоя, а молекулы ПАВ вытесняются на поверхность. Очевидно, что молекулы соли и сахара будут втянуты в жидкость, а молекулы воды вытеснены на поверхность. Таким образом, поверхностное натяжение – основное понятие физики и химии поверхностных явлений – представляет собой одну из наиболее важных характеристик и в практическом отношении. Следует отметить, что всякое серьёзное научное исследование в области физики гетерогенных систем требует измерения поверхностного натяжения. История экспериментальных методов определения поверхностного натяжения, насчитывающая более двух столетий, прошла путь от простых и грубых способов до прецизионных методик, позволяющих находить поверхностное натяжение с точностью до сотых долей процента. Интерес к этой проблеме особенно возрос в последние десятилетия в связи с выходом человека в космос, развитием промышленного строения, где капиллярные силы в различных устройствах часто играют определяющую роль.

Один из таких методов определения поверхностного натяжения основан на поднятии смачивающей жидкости между двумя стеклянными пластинками. Их следует опустить в сосуд с водой и постепенно сближать параллельно друг другу. Вода начнёт подниматься между пластинками – её будет втягивать сила поверхностного натяжения, о которой сказано выше. Легко рассчитать коэффициент поверхностного натяжения σ можно по высоте подъёма воды у и зазору между пластинками d.

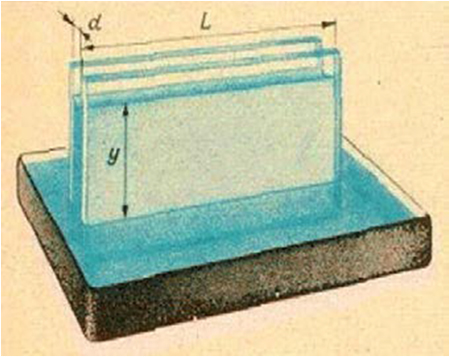
Сила поверхностного натяжения F = 2 σ L, где L – длина пластинки (двойка появилась из-за того, что вода соприкасается с обеими пластинками). Эта сила удерживает слой воды массы m = ρ Ldу, где ρ – плотность воды. Таким образом, 2 σ L = ρ Ldуg. Отсюда можно найти коэффициент поверхностного натяжения σ = 1/2( ρ gdу). (1)Но интереснее сделать так: с одного конца сжать пластинки вместе, а с другого оставить небольшой зазор.

Вода поднимется и образует между пластинками удивительно правильную поверхность. Сечение этой поверхности вертикальной плоскостью – гипербола. Для доказательства достаточно в формулу (1) вместо d подставить новое выражение для зазора в данном месте. Из подобия соответствующих треугольников (см. рис. 2) d = D (x/L). Здесь D – зазор на конце, L – по-прежнему длина пластинки, а x – расстояние от места соприкосновения пластинок до места, где определяется зазор и высота уровня. Таким образом, σ = 1/2( ρ gу)D(x/L), или у = 2 σ L/ ρ gD(1/х). (2)Уравнение (2) действительно является уравнением гиперболы.

Смачивание и несмачивание

Для детального изучения капиллярных явлений следует рассмотреть и некоторые молекулярные явления, обнаруживающиеся на трёхфазной границе сосуществования твёрдой, жидкой, газообразной фаз, в частности рассматривается соприкосновение жидкости с твёрдым телом. Если силы сцепления между молекулами жидкости больше, чем между молекулами твёрдого тела, то жидкость стремится уменьшить границу (площадь) своего соприкосновения с твёрдым телом, по возможности отступая от него. Капля такой жидкости на горизонтальной поверхности твёрдого тела примет форму сплюснутого шара. В этом случае жидкость называется несмачивающей твёрдое тело. Угол θ , образованный поверхностью твёрдого тела и касательной к поверхности жидкости, называется краевым. Для несмачивающей θ > 90°. В этом случае твёрдая поверхность, несмачиваемая жидкостью называется гидрофобной, или олоефильной. Если же силы сцепления между молекулами жидкости меньше, чем между молекулами жидкости и твёрдого тела, то жидкость стремится увеличить границу соприкосновения с твёрдым телом. В этом случае жидкость называется смачивающей твёрдое тело; краевой угол θ 90°. Поверхность же будет носить название гидрофильная. Случай, когда θ = 180°, называется полным несмачиванием. Однако это практически никогда не наблюдается, так как между молекулами жидкости и твёрдого тела всегда действуют силы притяжения. При θ = 0° наблюдается полное смачивание: жидкость растекается по всей поверхности твёрдого тела. Полное смачивание или полное несмачиваение являются крайними случаями. Между ними в зависимости от соотношения молекулярных сил промежуточное положение занимают переходные случаи неполного смачивания.

Смачиваемость и несмачиваемость – понятия относительные: жидкость,смачивающая одно твёрдое тело, может не смачивать другое тело. Например,вода смачивает стекло, но не смачивает парафин; ртуть не смачивает стекло, но смачивает медь.

Смачивание обычно трактуется как результат действия сил поверхностного натяжения. Пусть поверхностное натяжение на границе воздух – жидкость σ 1,2,на границе жидкость – твёрдое тело σ 1,3, на границе воздух – твёрдое тело σ 2,3.

На единицу длины периметра смачивания действуют три силы, численно равные σ 1,2, σ 2,3, σ 1,3, направленные по касательной к соответствующим границам раздела. В случае равновесия все силы должны уравновешивать друг друга. Силы σ 2,3 и σ 1,3 действуют в плоскости поверхности твёрдого тела, сила σ 1,2 направлена к поверхности под углом θ .

Условие равновесия межфазных поверхностей имеет следующий вид: σ 2,3 = σ 1,3 + σ 1,2cos θ или cos θ =( σ 2,3 − σ1 ,3)/ σ 1,2

Величину cos θ принято называть смачиванием и обозначать буквой В.

Определённое влияние на смачивание оказывает состояние поверхности. Смачиваемость резко меняется уже при наличии мономолекулярного слоя углеводородов. Последние же всегда присутствуют в атмосфере в достаточных количествах. Определённое влияние на смачивание оказывает и микрорельеф поверхности. Однако до настоящего времени пока не выявлена единая закономерность влияния шероховатости любой поверхности на смачивание её любой жидкостью. Например уравнение Венцеля-Дерягина cosθ = xcosθ0 связывает краевые углы жидкости на шероховатой ( θ ) и гладкой ( θ 0) поверхностях с отношением х площади истинной поверхности шероховатого тела к её проекции на плоскость. Однако на практике это уравнение не всегда соблюдается. Так, согласно этому уравнению в случае смачивания (θ 90 – к его увеличению (т.е. к большей гидрофобности). Исходя из этого и даются, как правило, сведения о влиянии шероховатости на смачивание.

По мнению многих авторов, скорость растекания жидкости на шероховатой поверхности ниже вследствие того, что жидкость при растекании испытывает задерживающее влияние встречающихся бугорков (гребней) шероховатостей. Необходимо отметить, что именно скорость изменения диаметра пятна, образованного строго дозированной каплей жидкости, нанесённой на чистую поверхность материала, используется в качестве основной характеристики смачивания в капиллярах. Её величина зависит как от поверхностных явлений, так и от вязкости жидкости, её плотности, летучести.

Очевидно, что более вязкая жидкость с прочими одинаковыми свойствами дольше растекается по поверхности и следовательно медленнее протекает по капиллярному каналу.

Капиллярные явления

Капиллярные явления, совокупность явлений, обусловленных поверхностным натяжением на границе раздела несмешивающихся сред (в системах жидкость - жидкость, жидкость - газ или пар) при наличии искривления поверхности. Частный случай поверхностных явлений.

Изучив подробно силы, лежащих в основе капиллярных явлений, стоит перейти непосредственно к капиллярам. Так, опытным путём можно пронаблюдать, что смачивающая жидкость (например, вода в стеклянной трубке) поднимается по капилляру. При этом, чем меньше радиус капилляра, тем на большую высоту поднимается в ней жидкость. Жидкость, не смачивающая стенки капилляра (например, ртуть с стеклянной трубке), опускается ниже уровня жидкости в широком сосуде. Так почему же смачивающая жидкость поднимается по капилляру, а несмачивающая опускается?

Не трудно заметить, что непосредственно у стенок сосуда поверхность жидкости несколько искривлена. Если молекулы жидкости, соприкасающиеся со стенкой сосуда, взаимодействуют с молекулами твёрдого тела сильнее, чем между собой, в этом случае жидкость стремится увеличить площадь соприкосновения с твёрдым телом (смачивающая жидкость). При этом поверхность жидкости изгибается вниз и говорят, что она смачивает стенки сосуда, в котором находится. Если же молекулы жидкости взаимодействуют между собой сильнее, чем с молекулами стенок сосуда, то жидкость стремится сократить площадь соприкосновения с твёрдым телом, её поверхность искривляется вверх. В этом случае говорят о несмачивании жидкостью стенок сосуда.

В узких трубочках, диаметр которых составляет доли миллиметра, искривлённые края жидкости охватывают весь поверхностный слой, и вся поверхность жидкости в таких трубочках имеет вид, напоминающий полусферу. Это так называемый мениск. Он может быть вогнутым, что наблюдается в случае смачивания, и выпуклым при несмачивании. Радиус кривизны поверхности жидкости при этом того же порядка, что и радиус трубки. Явления смачивания и несмачивания в данном случае также характеризуется краевым углом θ между смоченной поверхностью капиллярной трубки и мениском в точках их соприкосновения.

Под вогнутым мениском смачивающей жидкости давление меньше, чем под плоской поверхностью. Поэтому жидкость в узкой трубке (капилляре) поднимается до тех пор, пока гидростатическое давление поднятой в капилляре жидкости на уровне плоской поверхности не скомпенсирует разность давлений. Под выпуклым мениском несмачивающей жидкости давление больше, чем под плоской поверхностью, и это ведёт к опусканию несмачивающей жидкости.

Наличие сил поверхностного натяжения и кривизны поверхности жидкости в капиллярной трубочке ответственно за дополнительное давление под искривленной поверхностью, называемое давлением Лапласа: ∆p = ± 2 σ /R.

Так, условие равновесия жидкости в капиллярной трубочке определяется равенством

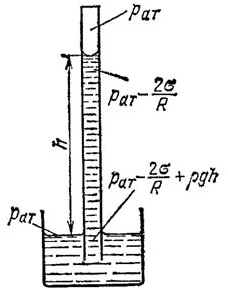
где ρ – плотность жидкости, h – высота её поднятия в трубочке, p₀ – атмосферное давление.

Из данного выражения следует, что h = 2 σ / ρ gR. (2)

Преобразуем полученную формулу, выразив радиус кривизны R мениска через радиус капиллярной трубочки r.

Из рис. 6.18 следует, что r = Rcos θ . Подставляя (1) в (2), получаем: h = 2 σ cos θ / ρ gr.

Полученная формула, определяющая высоту поднятия жидкости в капиллярной трубочке, носит название формулы Жюрена. Очевидно, что чем меньше радиус трубки, тем на большую высоту поднимается в ней жидкость. Кроме того, высота поднятия растёт с увеличением коэффициента поверхностного натяжения жидкости.

Подъём смачивающей жидкости по капилляру можно объяснить и по-другому. Как было сказано ранее, под действием сил поверхностного натяжения поверхность жидкости стремится сократиться. Вследствие этого поверхность вогнутого мениска стремится выпрямиться и сделаться плоской. При этом она тянет за собой частицы жидкости, лежащие под ней, и жидкость поднимается по капилляру вверх. Но поверхность жидкости в узкой трубке плоской оставаться не может, она должна иметь форму вогнутого мениска. Как только в новом положении данная поверхность примет форму мениска, она снова будет стремиться сократиться и т.д. В результате действия этих причин смачивающая жидкость и поднимается по капилляру. Поднятие прекратится, когда сила тяжести Fтяж поднятого столба жидкости, которая тянет поверхность вниз, уравновесит равнодействующую силу F сил поверхностного натяжения, направленных касательно к каждой точке поверхности.

По окружности соприкосновения поверхности жидкости со стенкой капилляра действует сила поверхностного натяжения, равная произведению коэффициента поверхностного натяжения на длину окружности: 2 σπ r, где r – радиус капилляра.

Сила тяжести, действующая на поднятую жидкость,

где ρ – плотность жидкости; h – высота столба жидкости в капилляре; g – устроение силы тяжести.

Подъём жидкости прекращается, когда F_тяж = F или ρπ r^2hg = 2 σπ r. Отсюда высота поднятия жидкости в капилляре h = 2 σ / ρ gR.

В случае несмачивающей жидкости последняя, стремясь сократить свою поверхность, будет опускаться вниз, выталкивая жидкость из капилляра.

Выведенная формула применима и для несмачивающей жидкости. В этом случае h – высота опускания жидкости в капилляре.

Капиллярные явления также весьма распространены в природе и часто используются в практической деятельности человека. Дерево, бумага, кожа, кирпич и очень многие другие предметы, окружающие нас, имеют капилляры. За счет капилляров вода поднимается по стеблям растений и впитывается в полотенце, когда мы им вытираемся. Поднятие воды по мельчайшим отверстиям в куске сахара, забор крови из пальца – это тоже примеры капиллярных явлений.

Кровеносная система человека, начинаясь с весьма толстых сосудов, заканчивается очень разветвленной сетью тончайших капилляров. Могут вызвать интерес, например, такие данные. Площадь поперечного сечения аорты равна 8 см 2 . Диаметр же кровеносного капилляра может быть в 50 раз меньше диаметра человеческого волоса при длине 0,5 мм. В теле взрослого человека имеется порядка 160 млрд капилляров. Их общая длина доходит до 80 тыс. км.

По многочисленным капиллярам, имеющимся в почве, вода из глубинных слоев поднимается к поверхности и интенсивно испаряется. Чтобы замедлить процесс потери влаги, капилляры разрушают путем разрыхления почвы с помощью борон, культиваторов, рыхлителей.

Практическая часть

Возьмем стеклянную трубочку с очень маленьким внутренним диаметром (d

КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ , поверхностные явления на границе жидкости с др. средой, связанные с искривлением ее пов-сти. Искривление пов-сти жидкости на границе с газовой фазой происходит в результате действия поверхностного натяжения жидкости, к-рое стремится сократить пов-сть раздела и придать ограниченному объему жидкости форму шара. Поскольку шар обладает миним. пов-стью при данном объеме, такая форма отвечает минимуму поверхностной энергии жидкости, т.е. ее устойчивому равновесному состоянию. В случае достаточно больших масс жидкости действие поверхностного натяжения компенсируется силой тяжести, поэтому маловязкая жидкость быстро принимает форму сосуда, в к-рый она налита, а ее своб. пов-сть представляется практически плоской. В отсутствие силы тяжести или в случае очень малых масс жидкость всегда принимает сферич. форму (капля), кривизна пов-сти к-рой определяет мн. св-ва в-ва. Поэтому К. я. ярко выражены и играют существ. роль в условиях невесомости, при дроблении жидкости в газовой среде (или распылении газа в жидкости) и образовании систем, состоящих из мн. капель или пузырьков ( эмульсий , аэрозолей , пен ), при зарождении новой фазы капель жидкости при конденсации паров, пузырьков пара при вскипании, зародышей кристаллизации. При контакте жидкости с конденсир. телами (др. жидкостью или твердым телом) искривление пов-сти раздела происходит в результате действия межфазного натяжения. В случае смачивания , напр., при соприкосновении жидкости с твердой стенкой сосуда, силы притяжения, действующие между молекулами твердого тела и жидкости, заставляют ее подниматься по стенке сосуда, вследствие чего примыкающий к стенке участок пов-сти жидкости принимает вогнутую форму. В узких каналах, напр., цилиндрич. капиллярах, образуется вогнутый мениск - полностью искривленная пов-сть жидкости (рис. 1).


Рис. 1. Капиллярное поднятие на высоту h жидкости, смачивающей стенки капилляра радиуса r; q - краевой угол смачивания.

Капиллярное давление. Т. к. силы поверхностного (межфазного) натяжения направлены по касательной к пов-сти жидкости, искривление последней ведет к появлению составляющей, направленной внутрь объема жидкости. В результате возникает капиллярное давление, величина к-рого D p связана со средним радиусом кривизны пов-сти r 0 ур-нием Лапласа:

D p = p 1 - p 2 = 2 s 12 /r 0 , (1)

где p 1 и p 2 - давления в жидкости 1 и соседней фазе 2 (газе или жидкости), s 12 - поверхностное (межфазное) натяжение. Если пов-сть жидкости вогнута (r 0 1 2 и D p 0 > 0) знак D p изменяется на обратный. Отрицат. капиллярное давление, возникающее в случае смачивания жидкостью стенок капилляра, приводит к тому, что жидкость будет всасываться в капилляр до тех пор, пока вес столба жидкости высотой h не уравновесит перепад давления D p. В состоянии равновесия высота капиллярного поднятия определяется ф-лой Жюрена:


где r 1 и r 2 - плотности жидкости 1 и среды 2, g - ускорение силы тяжести, r - радиус капилляра, q - краевой угол смачивания. Для несмачивающих стенки капилляра жидкостей cos q а = [2 s 12 /( r 1 — r 2 )g] 1/2 . Она имеет размерность длины и характеризует линейный размер Z [ а, при к-ром становятся существенными К. я. Так, для воды при 20 °С а = 0,38 см. При слабой гравитации (g : 0) значение а возрастает. На участке контакта частиц капиллярная конденсация приводит к стягиванию частиц под действием пониж. давления D p Уравнение Кельвина. Искривление пов-сти жидкости приводит к изменению над ней равновесного давления пара р по сравнению с давлением насыщ. пара p s над плоской пов-стью при той же т-ре Т. Эти изменения описываются ур-нием Кельвина:


где
- молярный объем жидкости, R - газовая постоянная. Понижение или повышение давления пара зависит от знака кривизны пов-сти: над выпуклыми пов-стями (r 0 > 0) p > p s ; над вогнутыми (r 0 р s . Так, над каплями давление пара повышено; в пузырьках, наоборот, понижено. На основании ур-ния Кельвина рассчитывают заполнение капилляров или пористых тел при капиллярной конденсации . Т. к. значения р различны для частиц разных размеров или для участков пов-сти, имеющей впадины и выступы, ур-ние (3) определяет и направление переноса в-ва в процессе перехода системы к состоянию равновесия. Это приводит, в частности, к тому, что относительно крупные капли или частицы растут за счет испарения (растворения) более мелких, а неровности пов-сти некристаллич. тела сглаживаются за счет растворения выступов и залечивания впадин. Заметные различия давления пара и р-римости имеют место лишь при достаточно малых r 0 (для воды, напр., при r 0 [ 0,1 мкм). Поэтому ур-ние Кельвина часто используется для характеристики состояния коллоидных систем и пористых тел и процессов в них.


Рис. 2. Перемещение жидкости на длину l в капилляре радиуса r; q - краевой угол.

Капиллярная пропитка. Понижение давления под вогнутыми менисками - одна из причин капиллярного перемещения жидкости в сторону менисков с меньшим радиусом кривизны. Частным случаем этого является пропитка пористых тел - самопроизвольное всасывание жидкостей в лиофильные поры и капилляры (рис. 2). Скорость v перемещения мениска в горизонтально расположенном капилляре (или в очень тонком вертикальном капилляре, когда влияние силы тяжести мало) определяется ур-нием Пуазёйля: [Пуазейля:]


где l - длина участка впитавшейся жидкости, h - ее вязкость, D p - перепад давления на участке l , равный капиллярному давлению мениска: D p = — 2 s 12 cos q /r. Если краевой угол q не зависит от скорости v, можно рассчитать кол-во впитавшейся жидкости за время t из соотношения:

l ( t ) = (rt s 12 cos q /2 h ) l/2 . (5)

Если q есть ф-ция v , то l и v связаны более сложными зависимостями. Ур-ния (4) и (5) используют для расчетов скорости пропитки при обработке древесины антисептиками, крашении тканей, нанесении катализаторов на пористые носители, выщелачивании и диффузионном извлечении ценных компонентов горных пород и др. Для ускорения пропитки часто используют ПАВ, улучшающие смачивание за счет уменьшения краевого угла q . Один из вариантов капиллярной пропитки - вытеснение из пористой среды одной жидкости другой, не смешивающейся с первой и лучше смачивающей пов-сть пор. На этом основаны, напр., методы извлечения остаточной нефти из пластов водными р-рами ПАВ, методы ртутной порометрии. Капиллярное впитывание в поры р-ров и вытеснение из пор несмешивающихся жидкостей, сопровождающиеся адсорбцией и диффузией компонентов, рассматриваются физико-химической гидродинамикой . Помимо описанных равновесных состояний жидкости и ее движения в порах и капиллярах, к К. я. относят также равновесные состояния очень малых объемов жидкости, в частности тонких слоев и пленок. Эти К. я. часто наз. К. я. II рода. Для них характерны, напр., зависимость поверхностного натяжения жидкости от радиуса капель и линейное натяжение. К. я. впервые исследованы Леонардо да Винчи (1561), Б. Паскалем (17 в.) и Дж. Жюреном (18 в.) в опытах с капиллярными трубками. Теория К. я. развита в работах П. Лапласа (1806), Т. Юнга (1804), А. Ю. Давыдова (1851), Дж. У. Гиббса (1876), И. С. Громеки (1879, 1886). Начало развития теории К. я. II рода положено трудами Б. В. Дерягина и Л. М. Щербакова. Лит.: Адамсон А., Физическая химия поверхностей, пер. с англ., М., 1979; Хейфец Л. И., Неймарк А. В., Многофазные процессы в пористых средах, М., 1982; Аксельруд Г. А., Альтшулер М. А., Введение в капиллярно-химическую технологию, М., 1983. Н. В. Чураев .