Мениск линза положение главных точек
Условие концентричности отдельной линзы в воздухе определяется равенством ее толщины разности радиусов:
Подставляя это значение толщины в формулу (11.34) для силы толстой линзы, получаем
Логарифмируя формулу (12.3) и дифференцируя по показателю, находим
Обращаясь к формуле (12.3), видим, что в случае, когда радиусы концентрической линзы имеют разные знаки, ее сила положительна. Если же оба радиуса имеют одинаковые знаки, то концентрическая линза станет концентрическим мениском и ее сила получится отрицательной.
Можно рассмотреть случай, когда радиусы толстой линзы будут равны друг другу; тогда первый член в формуле (11.34) обратится в нули сила мениска с равными радиусами выразится формулой
и будет всегда положительной.
Логарифмируя и дифференцируя формулу (12.5) по показателю преломления, определим величину хроматизма мениска с равными радиусами:
Существенно, что хроматизм такого мениска получается больше, чем у тонкой линзы.
Сопоставляя концентрический мениск и мениск с равными радиусами, видим, что при переходе от одного к другому и сила мениска и хроматизм переходят через нуль, только не одновременно.
Д. Д. Максутов обратил внимание на такой переход и поставил задачу получения мениска с исправленным хроматизмом.
Для решения такой задачи продифференцируем общее выражение для силы толстой линзы в воздухе:
Подставляя это значение толщины в общую формулу (11.34) для силы толстой линзы в воздухе, находим
и после сокращений
Формулы (12.11) и (12.13) позволяют определять все величины, характеризующие мениск Максутова.
Отметим ряд свойств мениска Максутова.
1. Мениск свободен от хроматизма положения в широком участке спектра и может рассматриваться как оптическая система, имеющая апохроматическую коррекцию.
2. Он обладает небольшой отрицательной оптической силой и положительной сферической аберрацией.
Изменяя отношение радиусов и соответственно изменяя толщину мениска, можно варьировать величину сферической аберрации при сохранении силы мениска неизменной.
3. Составляя на основании формулы (12.10) равенство
Все это позволяет рассматривать мениск Максутова как коррекционный элемент, позволяющий корригировать отрицательную сферическую аберрацию, не затрагивая исправления других аберраций оптической системы.
Основной трудностью при изготовлении мениска Максутова, как и других концентрических линз, является обеспечение хорошей взаимной центрировки мениска по отношению к его наружному диаметру.
Возвращаясь к рассмотрению концентрической линзы или системы концентрических линз, обратим внимание на то обстоятельство, что любой луч, вошедший по нормали к первой поверхности, выйдет по нормали ко второй или к последней поверхности, не изменяя своего направления. Поэтому для таких лучей будет сохраняться равенство углового увеличения единице.
Если система будет расположена в одной и той же среде, например в воздухе, то тогда и линейное увеличение окажется равным единице.
Таким образом, общий центр поверхностей концентрической линзы или системы концентрических поверхностей может рассматриваться в общем случае как совмещенные узловые точки или как главные точки, если система располагается в одной и той же среде.
Опираясь на это общее свойство концентрических линз, нетрудно получить выражение для оптической силы любого числа концентрических поверхностей.
Рассматривая концентрические системы как совокупность нескольких концентрических линз, совмещенных друг с другом, получаем, что их общая оптическая сила будет равна сумме составляющих сил:
Силу каждой из составляющих сил можно представить в виде
Суммируя силы двух смежных линз, можно предположить, что первый радиус последующей линзы будет равен второму радиусу предыдущей линзы. Тогда две такие линзы могут быть склеены друг с другом, причем образуется сила пары склеенных концентрических линз. В соответствии с этим можно написать
Заметим, что формула (12.19) известна как выражение для радиуса Петцваля в области аберраций третьего порядка.
Рассмотрим коцентрическую систему, составленную из нескольких поверхностей, разделенных средами с различными показателями преломления. Предположим, однако, что первая и последняя среды будут одинаковыми.
Рис. 12.1. К определению сферической аберрации концентрической системы
Очевидно, что система из любого числа концентрических поверхностей, разделенных любыми средами, но находящаяся в одной и той же среде, например в воздухе, будет обладать тем свойством, что расстояние от центра этой системы до входящего в нее луча должно быть равно расстоянию от этого же центра до луча, выходящего из системы.
Обращая подобную систему (т. е. последовательно заменяя первые радиусы, толщины и показатели преломления на последние и т. д. с соответствующим изменением знаков у радиусов на обратные) и сохраняя постоянным относительно центра системы ход входящего в нее луча, мы полностью сохраним и ход луча, выходящего из системы.
Так как не намечалось никаких ограничений для луча, входившего в концентрическую систему, то это свойство обратимости концентрической системы будет сохраняться для любого луча вплоть до момента, с которого прохождение луча через систему станет невозможным.
Простейшими базовыми элементами, определяющими оптическую силу, являются одиночные линзы в воздухе – базовые, или силовые линзы. Работа базовых линз должна наиболее полно использовать их коррекционные возможности для устранения главнейших полевых аберраций – астигматизма, комы, кривизны поверхности изображения. При использовании в базовых линзах только сферических поверхностей, они в некоторых случаях могут быть свободными от астигматизма, комы, сферической аберрации [1], а оптическая система, построенная из элементов, которые не будут обладать аберрациями, получится также свободной от этих же аберраций.
Исследование свойств сферической преломляющей поверхности показало, что такая поверхность получается свободной от астигматизма и комы в тех случаях, когда главный луч проходит через центр сферической поверхности или через ее апланатические точки. Также не будут обладать этими аберрациями сферические поверхности, совмещенные с изображением, и плоские поверхности в параллельном ходе лучей. Поэтому при создании базовых линз возможно устранение у них двух полевых аберраций – астигматизма и комы.
При создании базовых линз мы располагаем четырьмя видами сферических поверхностей: апланатические поверхности; поверхности, расположенные вблизи изображения или близфокальные; поверхности, концентричные зрачку; плоские поверхности.
Некоторые формы базовых линз обладают неисправленной кривизной поля зрения. Поэтому их использование требует введения коррекционных элементов, способных своей положительной кривизной обеспечить устранение общей кривизны поля. Очевидно, эти коррекционные элементы не должны вносить ни астигматизма, ни комы. И, соответственно, для их создания используются те же самые четыре вида поверхностей, свободных от астигматизма и комы (изопланатические поверхности), что и для создания базовых линз.
При использовании в качестве коррекционного элемента для исправления кривизны поля концентрическую линзу, ей придают определенную оптическую силу. Поэтому, варьируя величиной одного из ее радиусов и соответственно изменяя для сохранения силы ее второй радиус, можно влиять на величину сферической аберрации концентрической линзы и тем самым добиваться ее исправления в системах, не затрагивая астигматизма, комы и кривизны поля.
Для всех базовых элементов можно решить задачу исправления сферической аберрации путём введения и использования в них нормальной концентрической поверхности склейки, обладающей положительной сферической аберрацией.
Использование коррекционной концентрической линзы после систем, у которых поверхность изображения концентрична центру выходного зрачка, приводит к отнесению выпрямленного изображения в бесконечность, что равносильно преобразованию корригируемой системы в систему афокальную, или телескопическую. Можно корригировать всю телескопическую систему в отношении сферической аберрации. Оставляя между базовой и коррекционной линзами воздушный промежуток определенной величины, можно обеспечить двойную коррекцию сферической аберрации. Такая телеконцентрическая система может быть применена для перехода из жидкой среды в воздух с размещением материальной диафрагмы (входного зрачка) – на поверхности раздела жидкой и воздушной сред [1].
Используются также компенсационные системы, составленные из двух тонких линз, расположенных на конечном расстоянии друг от друга. Существует два вида компенсационных систем – системы типа телеобъективов с положительной линзой впереди и объективы с увеличенным передним отрезком с отрицательной линзой впереди.
В этих системах представляется возможным любую из линз полагать совмещенной с плоскостью материальной диафрагмы – зрачком входа или выхода. Астигматизм тонких линз, совмещенных с плоскостью материальной диафрагмы, не зависит от формы линз (их прогиба) и остается постоянным, что позволяет воспользоваться прогибом таких линз как коррекционным параметром для устранения комы всей системы. Вместе с тем прогиб тонкой линзы, не совпадающей с плоскостью зрачка, влияет на изменение астигматизма; этим можно воспользоваться для исправления астигматизма всей системы.
Рассмотрим основные виды апланатических точек преломляющей поверхности, представленной на рис.1, для которых устранена сферическая аберрация и соблюдено условие синусов.
 |
| Рис. 1. Сферическая преломляющая поверхность |
Известно, что сферическая преломляющая поверхность может иметь три пары сопряженных апланатических точек.
Первая пара: обе точки совпадают с вершиной поверхности s=s'=0, линейное увеличение b=+1. Вторая пара: обе точки совпадают с центром кривизны, т.е. s=s'=r; b=n/n?.
Третья пара: сопряженные точки расположены на расстояниях ѕ и ѕ' согласно следующим уравнениям:
Формы апланатических менисков. Обратимся к таблице 1, иллюстрирующей четыре формы апланатических менисков, которые могут дать апланатическое изображение точки на оси [1].
Передняя поверхность апланатична к положению предмета, центр второй поверхности совпадает с изображением от первой поверхности

Концентрический мениск – центры обеих поверхностей совпадают с положением предмета.

Обе поверхности действуют апланатически.

Центр передней поверхности совпадает с положением предмета, вторая поверхность апланатична к предмету

В качестве фронтальных компонентов в объективах с плоским полем часто применяются "толстые" мениски [2], которые позволяют исправить коэффициент Петцваля. Их особенностью является то, что изображение осевой точки предмета после преломления на первой поверхности совпадает с апланатической точкой третьего типа второй поверхности. Вторая поверхность мениска не вносит сферической аберрации, комы и астигматизма, в то время как первая поверхность, если предмет не расположен в ее центре кривизны, вносит эти аберрации. Кома и сферическая аберрация практически не достигают больших значений, так как рабочее расстояние объективов, в особенности высокоапертурных, невелико. Астигматизм, вносимый первой поверхностью, может достигать значительных величин, поскольку из условия исправления коэффициента Петцваля она обладает значительной кривизной.
 |
| Рис. 2. Фронтальный мениск |
На рис.2 изображен "толстый" фронтальный мениск. Предмет находится в точке S на расстоянии s1 от первой поверхности, а его изображение после преломления на первой поверхности совпадает с апланатической точкой второй поверхности. Буквами А1, А2 и А3 обозначены апланатические точки первой поверхности (первого, второго и третьего типа). Величина линейного поля у объективов микроскопа, в особенности сильных, невелика, а астигматизм мениска достаточно точно определяется аберрациями 3-го порядка.
Расположение предмета в апланатических точках первой поверхности нецелесообразно: в точке А1 отсутствует рабочее расстояние, так как s1=0; в точке А2 астигматизм близок к максимальной величине; в точке А3 апертура для последующей части не снижается, так как в этом случае линейное увеличение мениска равно единице.
При расчете объективов со средней или большой числовой апертурой целесообразно расположение предмета вблизи первой апланатической точки А1. Если s1=(0.1÷0.3)·r1, то увеличение фронтального мениска находится в пределах V=(2÷3)x, а астигматизм при этом вдвое меньше максимальной величины. Оптические материалы, используемые во фронтальных менисках, для достижения наибольших значений линейного увеличения и наилучшей коррекции хроматических аберраций должны иметь высокие значения показателя преломления и коэффициента средней дисперсии.
В качестве элементов последующей части можно использовать двух и трёхсклеенные компоненты. Исследование свойств трехлинзовых склеенных компонентов представляет особый интерес в связи с разработкой оптических систем с уменьшенным вторичным спектром. На базе этих компонентов могут быть получены схемные решения объективов микроскопов с форсированными оптическими характеристиками: повышенными числовыми апертурами и уменьшенной вуалирующей засветкой (объективы для исследования в отраженном свете). Трехлинзовый склеенный компонент по сравнению с двухлинзовым обладает лишним коррекционным параметром – оптической силой третьей линзы. Если рассматривается система с исправленным и уменьшенным вторичным спектром, целесообразно связать оптическую силу третьей линзы с величиной вторичного спектра [3]. Тогда оказывается возможным выразить основные параметры трехлинзового склеенного компонента через хроматические коэффициенты и постоянные оптических материалов. Расчет этих величин позволяет по заданным значениям аберраций третьего порядка и хроматическим аберрациям выбрать для компонента материалы линз и расположить их в нужном порядке.
При этом возможно выполнение расчета систем следующих типов:
- трёхлинзовые склеенные компоненты, составленные из трех различных материалов при n2≠n3≠n4 (базовые элементы для трехцветных апохроматов). При расчете трехлинзовых компонентов первого типа выбираются оптические материалы, предпочтительные для разработки трехцветных апохроматов: из группы лангкронов – флюорит или фторфосфатное стекло; из группы лангфлинтов – ТФ2, ТФ5; из группы курцфлинтов – ОФ4, СТК19. Сочетания этих материалов дают наименьшие значения оптических сил линз;
- трёхлинзовые склеенные компоненты, составленные из материалов, относительные частные дисперсии которых лежат на одной прямой;
- трёхлинзовые склеенные компоненты, наружные линзы которых выполнены из одного стекла при n2=n4 (базовые элементы для двухцветных апохроматов и систем с уменьшенным вторичным спектром). При расчёте трёхлинзовых компонентов с одинаковыми показателями преломления в наружных линзах выбираются материалы, рекомендуемые для расчета двухцветных апохроматов: в качестве лангкронов – флюорит, а в качестве курцфлинтов – ОФ4, СТК19, а также ряд обычных флинтов для разработки систем с уменьшенным вторичным спектром.
Вопросам расчета трехсклеенных апохоматических компонентов посвящен ряд работ ведущих оптотехников. В работе [4] изложен способ габаритного расчета такого компонента, даны рекомендации по выбору оптических материалов и приведен примерный алгоритм аберрационной коррекции.
В последующей части объектива часто также используются мениски конечной толщины, предложенные Богехольдом [5]. Применение этого элемента позволяет не только уменьшить сумму Петцваля, но и реализовать условие компактности габаритных размеров оптических систем планобъективов, высота которых стандартизирована.
 |
| Рис.3. Принципиальная схема последующей части объектива |
На рис.3 изображена принципиальная схема последующей части объектива, содержащая компенсационную систему (условно обозначенную совмещенными главными плоскостями НкНк') и мениск. Положение плоскости предмета компенсационной системы sк известно из расчета фронтальной части объектива; положение плоскости изображения определяется как sк'≈sк*vк, где vк – увеличение компенсационной системы.
При анализе аберрационных свойств мениска в качестве переменных параметров можно использовать увеличение мениска vм и его передний отрезок sм. Если принять, что положение последней поверхности мениска совпадает с опорной плоскостью объектива, а объектив рассчитан для работы с конечной длиной тубуса, то можно получить соотношения радиусов кривизны поверхностей через значения углов и высот первого параксиального луча:
α1 = 1/ νм
h1 = - sм'/ νм
α2 = (- sм' + sм νм)/ νмd
h2 = - sм
α3 = 1
Толщина мениска d может быть использована в качестве коррекционного параметра.
При этом справедливы следующие соображения:
- для выбранного увеличения νм существует область конструктивных решений, определяемая отрезком sм, в которой радиусы кривизны менисков имеют приемлемые для практической реализации значения;
- коррекционные возможности менисков в отношении компенсации остаточных аберраций фронтальных систем весьма ограничены. Хроматизм увеличения значителен и противоположен по знаку хроматизму увеличения фронтальной части;
- увеличение отрезка sм при выбранном значении νм целесообразно не только для усиления компенсационных свойств мениска, но и для снижения относительных отверстий компонентов компенсационной системы.
Для определения хроматических аберраций мениска вычисляются хроматические коэффициенты C1 и C2 для наружных поверхностей мениска:
C1 = (α1 - α2)/ ν;
C2 = (α2 - 1)/ ν.
Если при введении в мениск радиуса ахроматизации rскл считать, что кроновая и флинтовая линзы выполнены из марок стекол, имеющих равные значения показателей преломления для основной длины волны, то хроматический коэффициент склеенной поверхности, разделяющей две среды с равными показателями преломления для основной длины волны, будет определяться выражением:
Cскл = (n–1)(1/ν3 –1/ν2)(α2–hскл/rскл).
где hскл – высота первого параксиального луча на склеенной поверхности,
hскл=h1–α2d1, где d1 – толщина первой линзы, выбираемая по конструктивным соображениям; ν2 , ν3 – коэффициенты дисперсии материалов.
Для получения компенсационного для фронтальной части хроматизма увеличения последующей части необходимы большие значения хроматического коэффициента Cскл, что приводит к отрицательной хроматической разности положений и увеличивает тем самым коррекционную нагрузку системы.
Введение разности показателей преломления для основной длины волны в материалах кроновой и флинтовой линз мениска не изменяет заметным образом состояние его аберрационной коррекции.
В результате исследования свойств отдельных элементов объективов построение последующей части планобъектива представляется как процесс оптимизации параметров компенсационной системы и мениска конечной толщины.
Линзы, как правило, имеют сферическую или близкую к сферической поверхность. Они могут быть вогнутыми, выпуклыми или плоскими (радиус равен бесконечности). Обладают двумя поверхностями, через которые проходит свет. Они могут сочетаться по-разному, образуя различные виды линз (фото приведено далее в статье):
- Если обе поверхности выпуклые (изогнуты наружу), центральная часть толще, чем по краям.
- Линза с выпуклой и вогнутой сферами называется мениском.
- Линза с одной плоской поверхностью носит название плоско-вогнутой или плоско-выпуклой, в зависимости от характера другой сферы.
Как определить вид линзы? Остановимся на этом подробнее.
Собирающие линзы: виды линз
Независимо от сочетания поверхностей, если их толщина в центральной части больше, чем по краям, они называются собирающими. Имеют положительное фокусное расстояние. Различают следующие виды собирающих линз:
- плоско-выпуклые,
- двояковыпуклые,
- вогнуто-выпуклые (мениск).
Рассеивающие линзы: виды линз
Если их толщина в центре тоньше, чем по краям, то они носят название рассеивающих. Имеют отрицательное фокусное расстояние. Существуют такие виды рассеивающих линз:
- плоско-вогнутые,
- двояковогнутые,
- выпукло-вогнутые (мениск).

Базовые понятия
Лучи от точечного источника расходятся из одной точки. Их называют пучком. Когда пучок входит в линзу, каждый луч преломляется, изменяя свое направление. По этой причине пучок может выйти из линзы в большей или меньшей степени расходящимся.
Некоторые виды оптических линз изменяют направление лучей настолько, что они сходятся в одной точке. Если источник света расположен, по меньшей мере, на фокусном расстоянии, то пучок сходится в точке, удаленной, по крайней мере, на ту же дистанцию.
Действительные и мнимые изображения
Точечный источник света называется действительным объектом, а точка сходимости пучка лучей, выходящего из линзы, является его действительным изображением.
Важное значение имеет массив точечных источников, распределенных на, как правило, плоской поверхности. Примером может служить рисунок на матовом стекле, подсвеченный сзади. Другим примером является диафильм, освещенный сзади так, чтобы свет от него проходил через линзу, многократно увеличивающую изображение на плоском экране.
В этих случаях говорят о плоскости. Точки на плоскости изображения 1:1 соответствуют точкам на плоскости объекта. То же относится и к геометрическим фигурам, хотя полученная картинка может быть перевернутой по отношению к объекту сверху вниз или слева направо.
Схождение лучей в одной точке создает действительное изображение, а расхождение – мнимое. Когда оно четко очерчено на экране – оно действительное. Если же изображение можно наблюдать, только посмотрев через линзу в сторону источника света, то оно называется мнимым. Отражение в зеркале – мнимое. Картину, которую можно увидеть через телескоп – тоже. Но проекция объектива камеры на пленку дает действительное изображение.

Фокусное расстояние
Фокус линзы можно найти, пропустив через нее пучок параллельных лучей. Точка, в которой они сойдутся, и будет ее фокусом F. Расстояние от фокальной точки до объектива называют его фокусным расстоянием f. Параллельные лучи можно пропустить и с другой стороны и таким образом найти F с двух сторон. Каждая линза обладает двумя F и двумя f. Если она относительно тонка по сравнению с ее фокусными расстояниями, то последние приблизительно равны.
Дивергенция и конвергенция
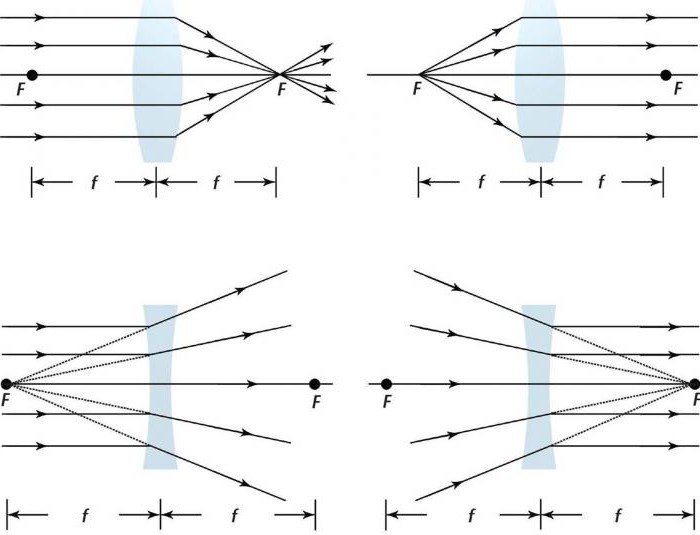
Положительным фокусным расстоянием характеризуются собирающие линзы. Виды линз данного типа (плоско-выпуклые, двояковыпуклые, мениск) сводят лучи, выходящие из них, больше, чем они были сведены до этого. Собирающие объективы могут формировать как действительное, так и мнимое изображение. Первое формируется только в случае, если расстояние от линзы до объекта превышает фокусное.
Отрицательным фокусным расстоянием характеризуются рассеивающие линзы. Виды линз этого типа (плоско-вогнутые, двояковогнутые, мениск) разводят лучи больше, чем они были разведены до попадания на их поверхность. Рассеивающие линзы создают мнимое изображение. И только когда сходимость падающих лучей значительна (они сходятся где-то между линзой и фокальной точкой на противоположной стороне), образованные лучи все еще могут сходиться, образуя действительное изображение.
Важные различия
Луч, который с расстоянием отдаляется от оптической оси, называется расходящимся. А тот, который к ней становится ближе, носит название сходящегося. Лучи, параллельные оптической оси, имеют нулевое схождение или расхождение. Таким образом, когда говорят о схождении или расхождении одного луча, его соотносят с оптической осью.
Некоторые виды линз, физика которых такова, что луч отклоняется в большей степени к оптической оси, являются собирающими. В них сходящиеся лучи сближаются еще больше, а расходящиеся отдаляются меньше. Они даже в состоянии, если их сила достаточна для этого, сделать пучок параллельным или даже сходящимся. Аналогично рассеивающая линза может развести расходящиеся лучи еще больше, а сходящиеся – сделать параллельными или расходящимися.

Увеличительные стекла
Линза с двумя выпуклыми поверхностями толще в центре, чем по краям, и может использоваться в качестве простого увеличительного стекла или лупы. При этом наблюдатель смотрите через нее на мнимое, увеличенное изображение. Объектив камеры, однако, формирует на пленке или сенсоре действительное, как правило, уменьшенное в размерах по сравнению с объектом.
Способность линзы изменять сходимость света называется ее силой. Выражается она в диоптриях D = 1 / f, где f – фокусное расстояние в метрах.
У линзы с силой 5 диоптрий f = 20 см. Именно диоптрии указывает окулист, выписывая рецепт очков. Скажем, он записал 5,2 диоптрий. В мастерской возьмут готовую заготовку в 5 диоптрий, полученную на заводе-изготовителе, и отшлифуют немного одну поверхность, чтобы добавить 0,2 диоптрии. Принцип состоит в том, что для тонких линз, в которых две сферы расположены близко друг к другу, соблюдается правило, согласно которому общая их сила равна сумме диоптрий каждой: D = D1 + D2.

Труба Галилея
Во времена Галилея (начало XVII века), очки в Европе были широко доступны. Они, как правило, изготавливались в Голландии и распространялись уличными торговцами. Галилео слышал, что кто-то в Нидерландах поместил два вида линз в трубку, чтобы удаленные объекты казались больше. Он использовал длиннофокусный собирающий объектив в одном конце трубки, и короткофокусный рассеивающий окуляр на другом конце. Если фокусное расстояние объектива равно fo и окуляра fe, то дистанция между ними должна быть fo-fe, а сила (угловое увеличение) fo/fe. Такая схема называется трубой Галилея.
Телескоп обладает увеличением 5 или 6 крат, сравнимым с современными ручными биноклями. Этого достаточно для многих захватывающих астрономических наблюдений. Можно без проблем увидеть лунные кратеры, четыре луны Юпитера, кольца Сатурна, фазы Венеры, туманности и звездные скопления, а также слабые звезды в Млечном Пути.

Телескоп Кеплера
Кеплер услышал обо всем этом (он и Галилей вели переписку) и построил еще один вид телескопа с двумя собирающими линзами. Та, у которой большое фокусное расстояние, является объективом, а та, у которой оно меньше – окуляром. Расстояние между ними равно fo + fe, а угловое увеличение составляет fo/fe. Этот кеплеровский (или астрономический) телескоп создает перевернутое изображение, но для звезд или луны это не имеет значения. Данная схема обеспечила более равномерное освещение поля зрения, чем телескоп Галилея, и была более удобна в использовании, так как позволяла держать глаза в фиксированном положении и видеть все поле зрения от края до края. Устройство позволяло достичь более высокого увеличения, чем труба Галилея, без серьезного ухудшения качества.
Оба телескопа страдают от сферической аберрации, в результате чего изображения не полностью сфокусированы, и хроматической аберрации, создающей цветные ореолы. Кеплер (и Ньютон) считал, что эти дефекты невозможно преодолеть. Они не предполагали, что возможны ахроматические виды линз, физика которых станет известна лишь в XIX веке.

Зеркальные телескопы
Грегори предположил, что в качестве объективов телескопов можно использовать зеркала, так как в них отсутствует цветная окантовка. Ньютон воспользовался этой идеей и создал ньютоновскую форму телескопа из вогнутого посеребренного зеркала и положительного окуляра. Он передал образец Королевскому обществу, где тот находится и по сей день.
Однолинзовый телескоп может проецировать изображение на экран или фотопленку. Для должного увеличения требуется положительная линза с большим фокусным расстоянием, скажем, 0,5 м, 1 м или много метров. Такая компоновка часто используется в астрономической фотографии. Людям, незнакомым с оптикой, может показаться парадоксальной ситуация, когда более слабая длиннофокусная линза дает большее увеличение.
Сферы
Высказывались предположения, что древние культуры, возможно, имели телескопы, потому что они делали маленькие стеклянные шарики. Проблема состоит в том, что неизвестно, для чего они использовались, и они, конечно, не могли бы лечь в основу хорошего телескопа. Шарики могли применяться для увеличения мелких объектов, но качество при этом вряд ли было удовлетворительным.
Фокусное расстояние идеальной стеклянной сферы очень короткое и формирует действительное изображение очень близко от сферы. Кроме того, аберрации (геометрические искажения) значительные. Проблема кроется в расстоянии между двумя поверхностями.
Однако если сделать глубокую экваториальную канавку, чтобы блокировать лучи, которые вызывают дефекты изображения, она превращается из очень посредственной лупы в прекрасную. Такое решение приписывается Коддингтону, а увеличитель его имени можно приобрести сегодня в виде небольших ручных луп для изучения очень маленьких объектов. Но доказательств того, что это было сделано до 19-го века, нет.
Читайте также:


