Основные элементарные функции и их графики шпора
Дата добавления: 2014-04-28 ; просмотров: 21840 ; Нарушение авторских прав
Определение 2. Основными элементарными функциями принято называть степенную, показательную, логарифмическую, тригонометрические и обратные тригонометрические функции. Ниже приведены графики этих функций, которые наглядно характеризуют их основные свойства.
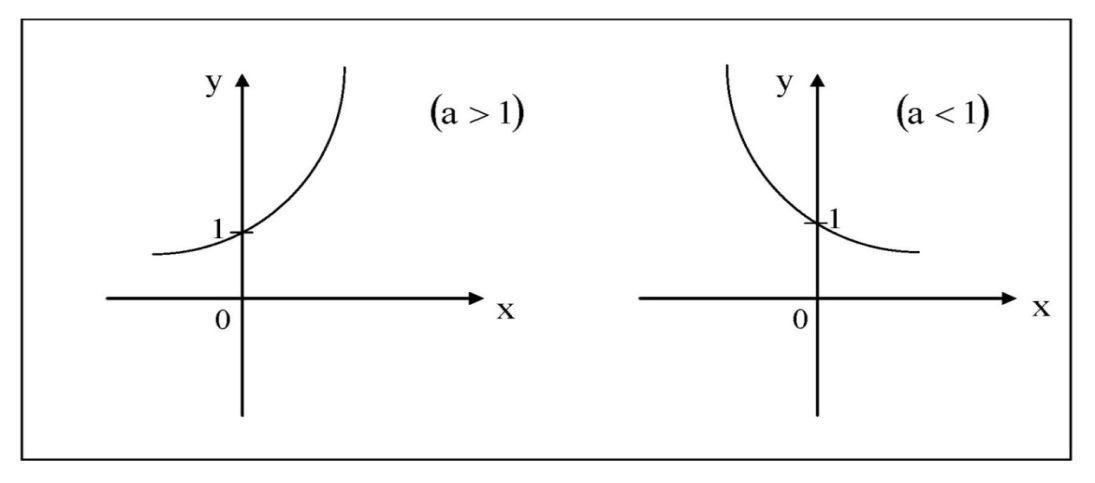
1) Показательная функция y = α x , a>0, a¹ 1;
2) Степенная функция y = x α , α ∈ R .
Графики степенных функций, соответствующих различным показателям степени, представлены на рис. 2

3) Логарифмическая функция y = logax, a> 0, a¹ 1;

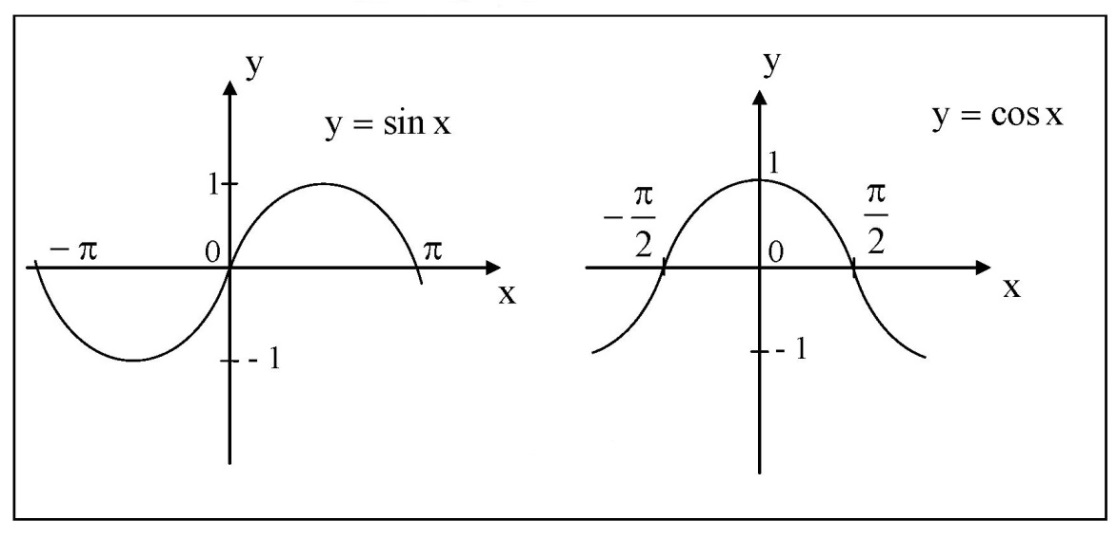
4) Тригонометрические функцииy = sinx, y = cosx,
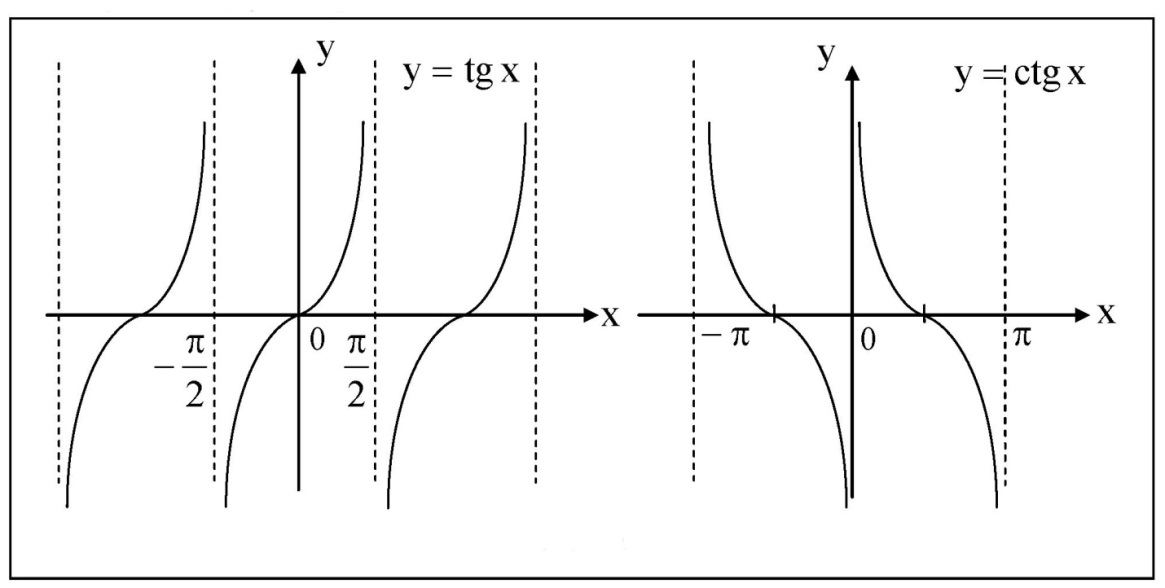
y = tgx, y = ctgx
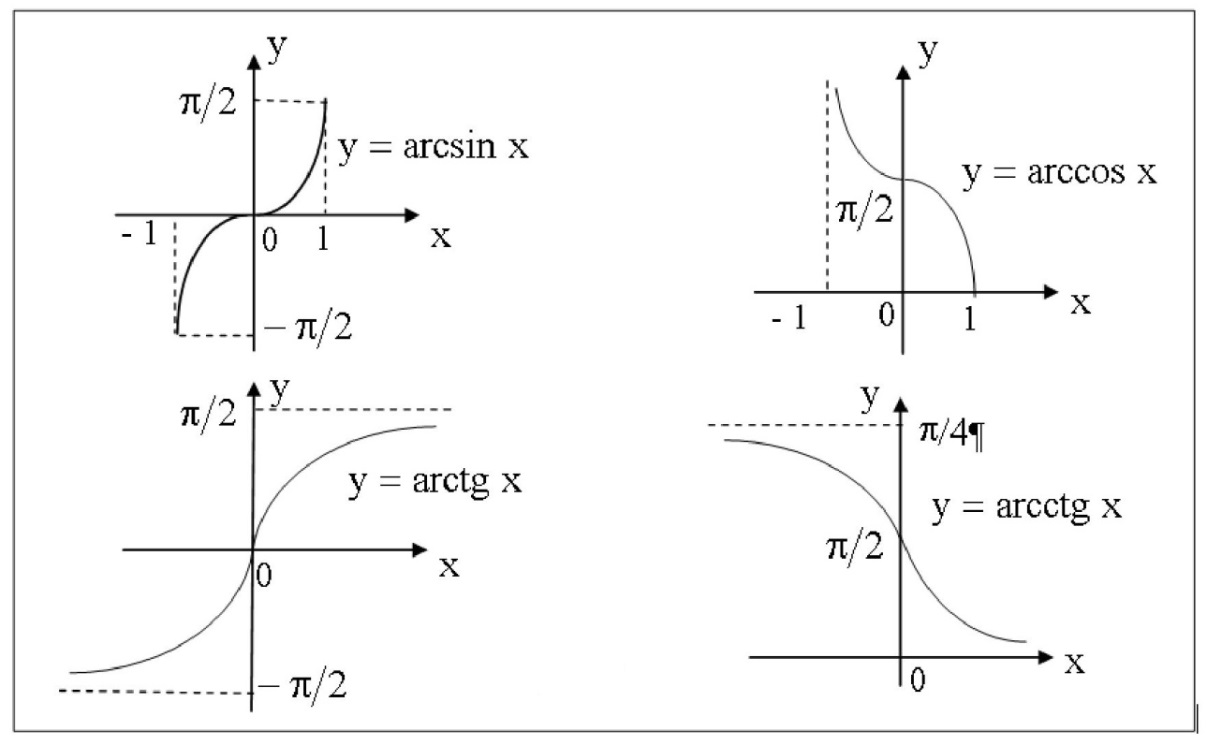
5) Обратные тригонометрические функции
y = arcsinx, D (f) = [-1; 1], E (f) = 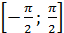
;
y = arccos x, D (f ) = [- 1; l], E (f) = 
;
y = arctg x, D (f) = R, E (f) = 
;
y = arcctg x, D (f) = R, E (f) = 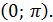
Функция, задаваемая одной формулой, составленной из основных элементарных функций и постоянных величин с помощью конечного числа арифметических операций сложения, вычитания, умножения, деления и операций взятия функции от функции, называется элементарной функцией.
Примерами элементарных функций являются:
у = ax + b–линейная функция a,b∈ R;
у = ax + bx + c– квадратичная функция a, b, с ∈ R;
у = 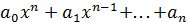
– целая рациональная функция или многочлен степениn, 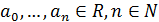
;
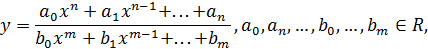
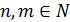
– дробно‒рациональная функция; частным случаем дробно‒рациональной функции является дробно‒линейная функция 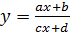
, 
.
Примерами неэлементарных функций могут служить
у =sinx = 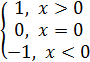
, у = 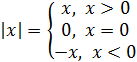
Данный методический материал носит справочный характер и относится к широкому кругу тем. В статье приведен обзор графиков основных элементарных функций и рассмотрен важнейший вопрос – как правильно и БЫСТРО построить график. В ходе изучения высшей математики без знания графиков основных элементарных функций придётся тяжело, поэтому очень важно вспомнить, как выглядят графики параболы, гиперболы, синуса, косинуса и т.д., запомнить некоторые значения функций. Также речь пойдет о некоторых свойствах основных функций.
Я не претендую на полноту и научную основательность материалов, упор будет сделан, прежде всего, на практике – тех вещах, с которыми приходится сталкиваться буквально на каждом шагу, в любой теме высшей математики. Графики для чайников? Можно сказать и так.
По многочисленным просьбам читателей кликабельное оглавление:
Кроме того, есть сверхкраткий конспект по теме
– освойте 16 видов графиков, изучив ШЕСТЬ страниц!
Серьёзно, шесть, удивился даже я сам. Данный конспект содержит улучшенную графику и доступен за символическую плaту, демо-версию можно посмотреть здесь. Файл удобно распечатать, чтобы графики всегда были под рукой. Спасибо за поддержку проекта!
И сразу начинаем:
Как правильно построить координатные оси?
На практике контрольные работы почти всегда оформляются студентами в отдельных тетрадях, разлинованных в клетку. Зачем нужна клетчатая разметка? Ведь работу, в принципе, можно сделать и на листах А4. А клетка необходима как раз для качественного и точного оформления чертежей.
Любой чертеж графика функции начинается с координатных осей.
Чертежи бывают двухмерными и трехмерными.
Сначала рассмотрим двухмерный случай декартовой прямоугольной системы координат:
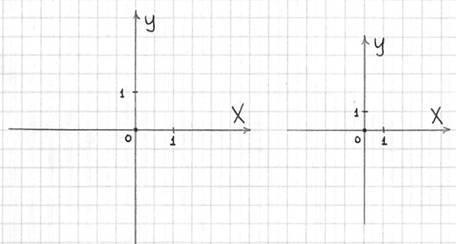
3) Задаем масштаб по осям: рисуем ноль и две единички. При выполнении чертежа самый удобный и часто встречающийся масштаб: 1 единица = 2 клеточки (чертеж слева) – по возможности придерживайтесь именно его. Однако время от времени случается так, что чертеж не вмещается на тетрадный лист – тогда масштаб уменьшаем: 1 единица = 1 клеточка (чертеж справа). Редко, но бывает, что масштаб чертежа приходится уменьшать (или увеличивать) еще больше
Кстати, о сантиметрах и тетрадных клетках. Правда ли, что в 30 тетрадных клетках содержится 15 сантиметров? Отмерьте в тетради для интереса 15 сантиметров линейкой. В СССР, возможно, это было правдой… Интересно отметить, что если отмерить эти самые сантиметры по горизонтали и вертикали, то результаты (в клетках) будут разными! Строго говоря, современные тетради не клетчатые, а прямоугольные. Возможно, это покажется ерундой, но, чертить, например, окружность циркулем при таких раскладах очень неудобно. Если честно, в такие моменты начинаешь задумываться о правоте товарища Сталина, который отправлял в лагеря за халтуру на производстве, не говоря уже об отечественном автомобилестроении, падающих самолетах или взрывающихся электростанциях.
Дополнительно: вИдение прямоугольной системы координат глазами аналитической геометрии освещается в статье Линейная (не) зависимость векторов. Базис векторов, подробную информацию о координатных четвертях можно найти во втором параграфе урока Линейные неравенства.
Трехмерный случай
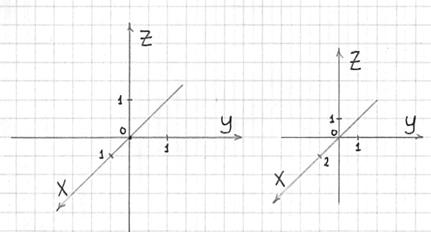
Здесь почти всё так же.
2) Подписываем оси.
. Для чего нужны все эти правила? Правила существуют для того, чтобы их нарушать. Чем я сейчас и займусь. Дело в том, что последующие чертежи статьи будут выполнены мной в Экселе, и, координатные оси будут выглядеть некорректно с точки зрения правильного оформления. Я бы мог начертить все графики от руки, но чертить их на самом деле жуть как неохота Эксель их начертит гораздо точнее.
Графики и основные свойства элементарных функций
График линейной функции
Берем еще какую-нибудь точку, например, 1.
При оформлении заданий координаты точек обычно сводятся в таблицу:
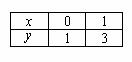
А сами значения рассчитываются устно или на черновике, калькуляторе.
Две точки найдены, выполним чертеж:
Не лишним будет вспомнить частные случаи линейной функции:
Построение прямой – самое распространенное действие при выполнении чертежей.
Прямая линия детально рассматривается в курсе аналитической геометрии, и желающие могут обратиться к статье Уравнение прямой на плоскости.
График квадратичной, кубической функции, график многочлена
При изучении пределов функций желательно понимать геометрический смысл предела.
Я не случайно так подробно расписал свойства функции, все вышеперечисленные вещи полезно знать и помнить при построении графиков функций, а также при исследовании графиков функций.
В этом примере мы рассмотрим важный технический вопрос: Как быстро построить параболу? В практических заданиях необходимость начертить параболу возникает очень часто, в частности, при вычислении площади фигуры с помощью определенного интеграла. Поэтому чертеж желательно научиться выполнять быстро, с минимальной потерей времени. Я предлагаю следующий алгоритм построения.
Сначала находим вершину параболы. Для этого берём первую производную и приравниваем ее к нулю:
Если с производными плохо, следует ознакомиться с уроком Как найти производную?
В каком порядке находить остальные точки, думаю, будет понятно из итоговой таблицы:

Углублённые знания о кривой можно получить на уроке Гипербола и парабола.
Кубическая парабола

Функции-многочлены 4-й, 6-й и других четных степеней имеют график принципиально следующего вида:
Он представляет собой одну из ветвей параболы. Выполним чертеж:
То есть, график функции полностью находится в первой координатной четверти.

График гиперболы
Такая прямая (к которой бесконечно близко приближается график какой-либо функции) называется асимптотой.
Будет ГРУБОЙ ошибкой, если при оформлении чертежа по небрежности допустить пересечение графика с асимптотой.
Указанную закономерность места жительства гиперболы нетрудно проанализировать с точки зрения геометрических преобразований графиков.

Детальную геометрическую информацию о рассмотренной линии можно найти в статье Гипербола и парабола.
График показательной функции

Должен сказать, что второй случай встречается на практике реже, но он встречается, поэтому я счел нужным включить его в данную статью.
График логарифмической функции

Если позабылось, что такое логарифм, пожалуйста, обратитесь к школьным учебникам.
Графики тригонометрических функций
С чего начинаются тригонометрические мучения в школе? Правильно. С синуса
Данная линия называется синусоидой.
График косинуса
Поэтому почти все свойства синуса справедливы и для косинуса. За некоторым, но существенным исключением.
Графики тангенса и котангенса
Графики обратных тригонометрических функций
Свойства арккотангенса вы вполне сможете сформулировать самостоятельно. Отмечу, что арккотангенс, как и арккосинус, не является четной или нечетной функцией.
Пожалуй, для начала хватит. К этой странице придется частенько обращаться в ходе изучения самых различных разделов курса высшей математики.
Ну что, смертнички, полетаем? =)
Тогда надеваем парашюты и готовимся к преобразованиям графиков.
(Переход на главную страницу)
Набор функций, которые мы можем построить достаточно невелик. Однако, большинство функций строятся с помощью четырёх арифметических операций и суперпозиций (или, по-другому, комбинаций) основных элементарных функций.
К числу основных элементарных функций относятся:
1. Прямая задаётся уравнением $y=x$ и её график имеет вид:
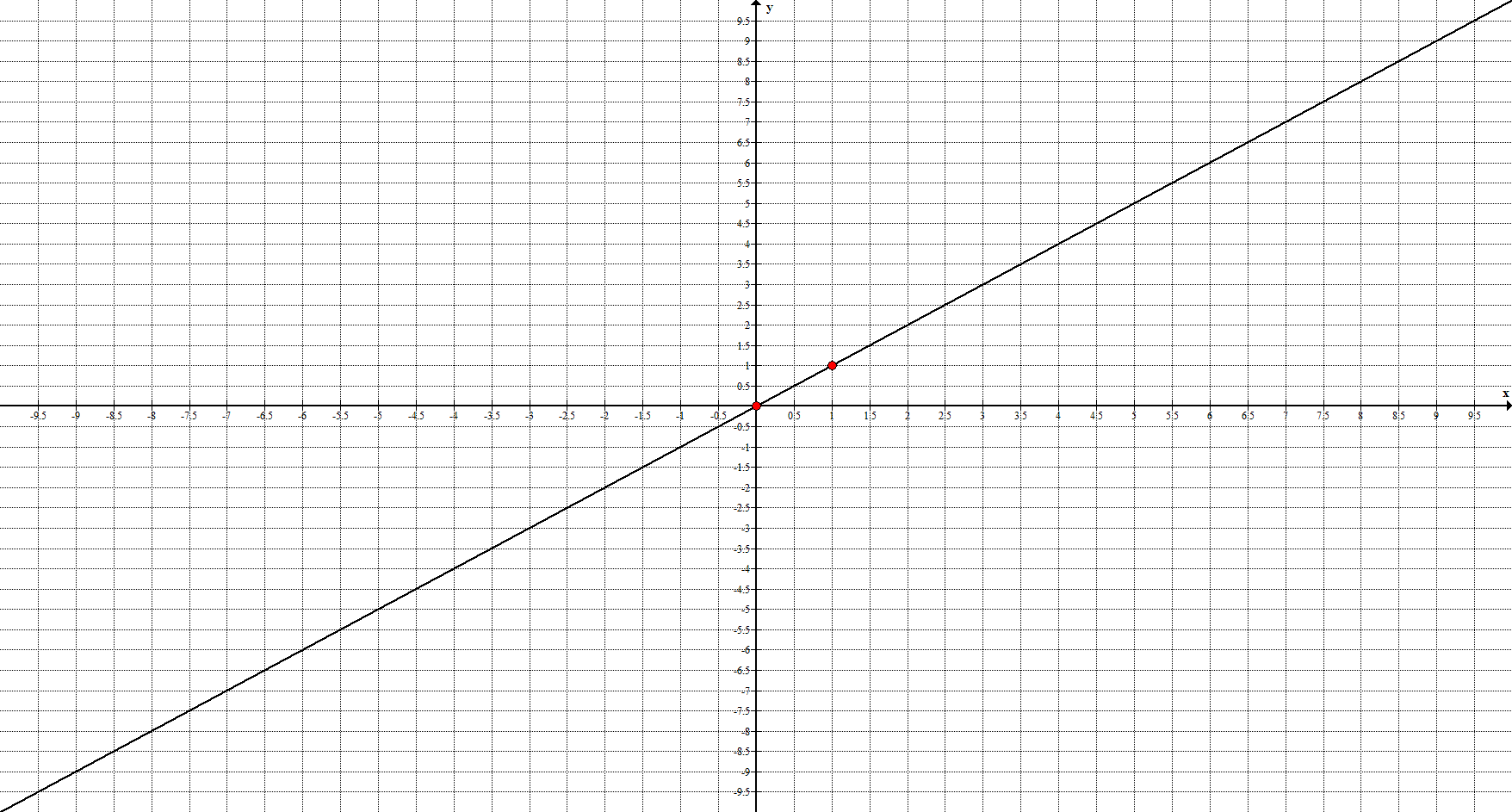
Ключевые точки: $(0;0), \ (1;1)$
2. Гипербола (или обратная пропорциональность) задаётся уравнением $y=\frac<1>
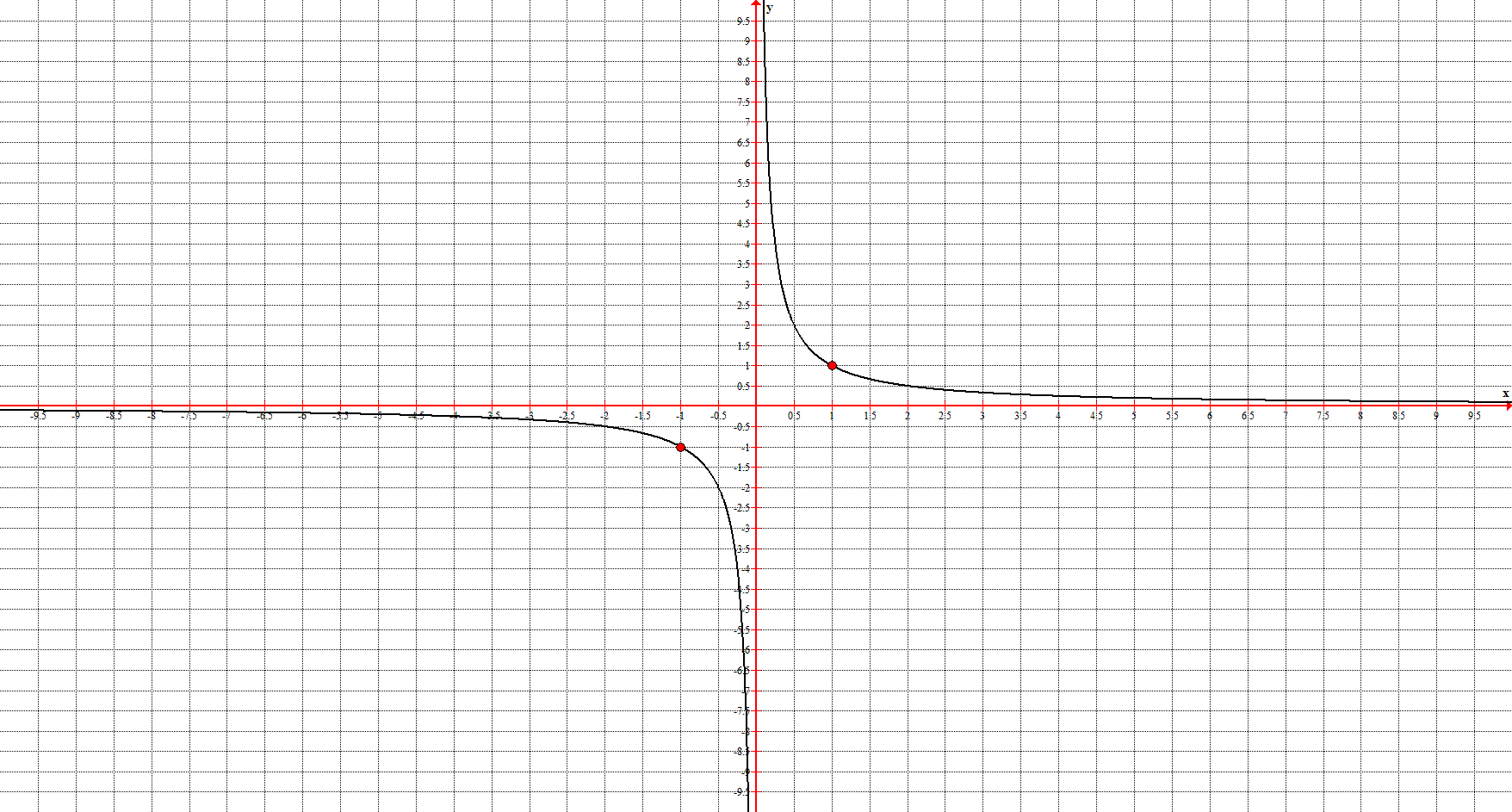
Асимптоты: $x=0, \ y=0$
Ключевые точки: $(-1;1), \ (1;1)$
3. Парабола задаётся уравнением $y=x^2$ и её график имеет вид:
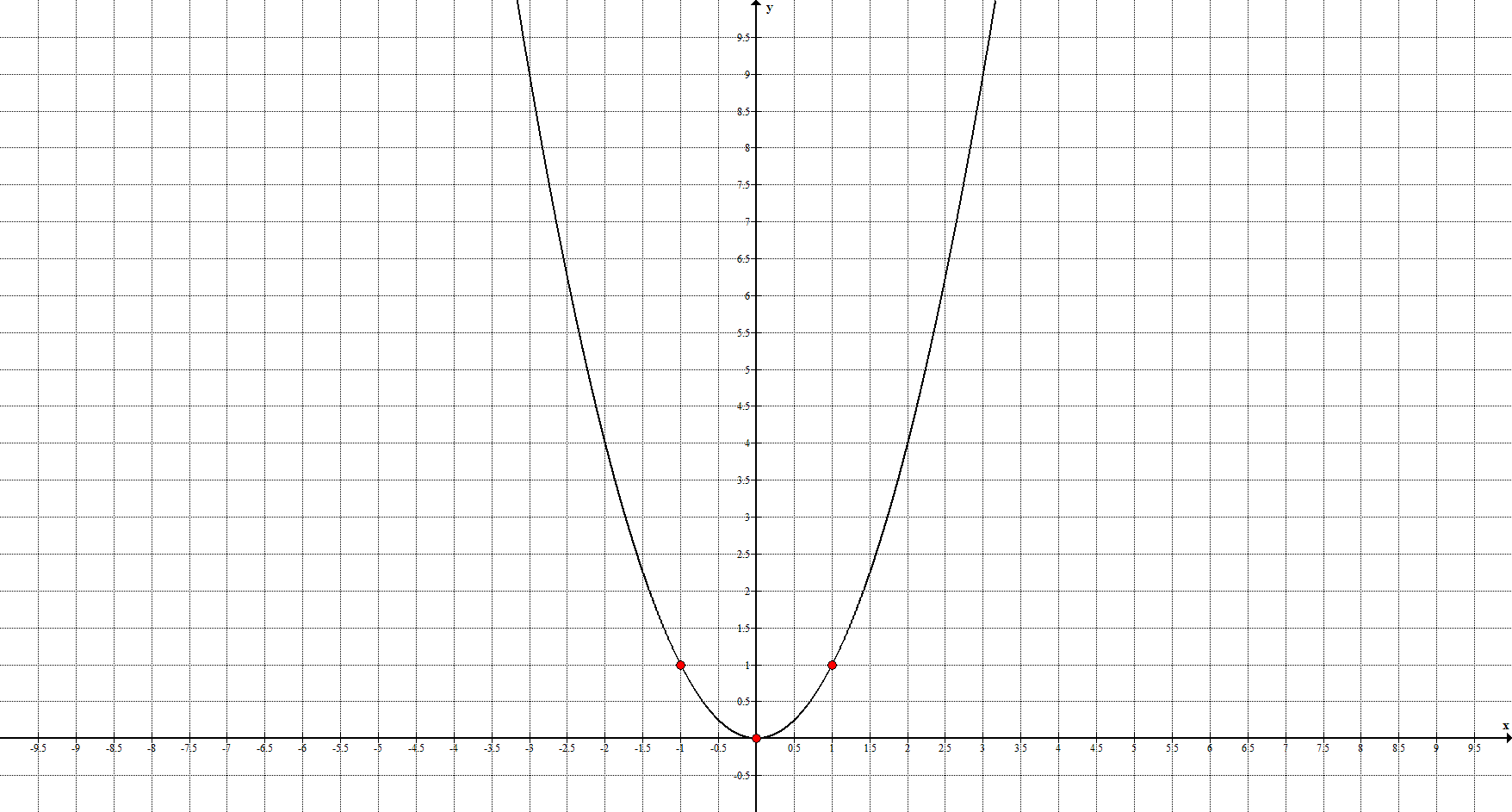
Ключевые точки: $(-1;1), \ (0;0), \ (1;1)$
4. Кубическая парабола задаётся уравнением $y=x^3$ и её график имеет вид:
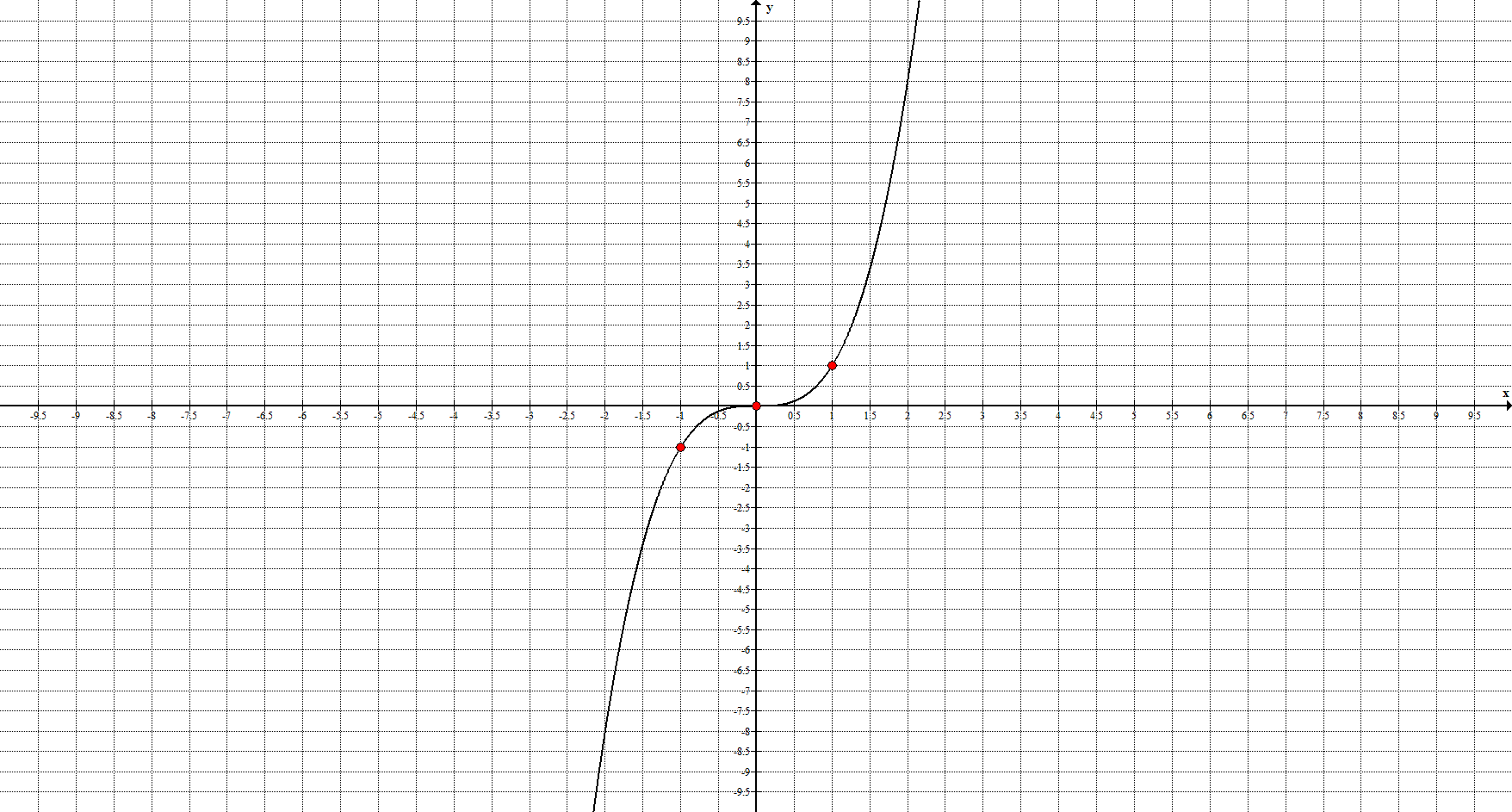
Ключевые точки: $(-1;-1), \ (0;0), \ (1;1)$
5. Коренная функция задаётся уравнением $y=\sqrt
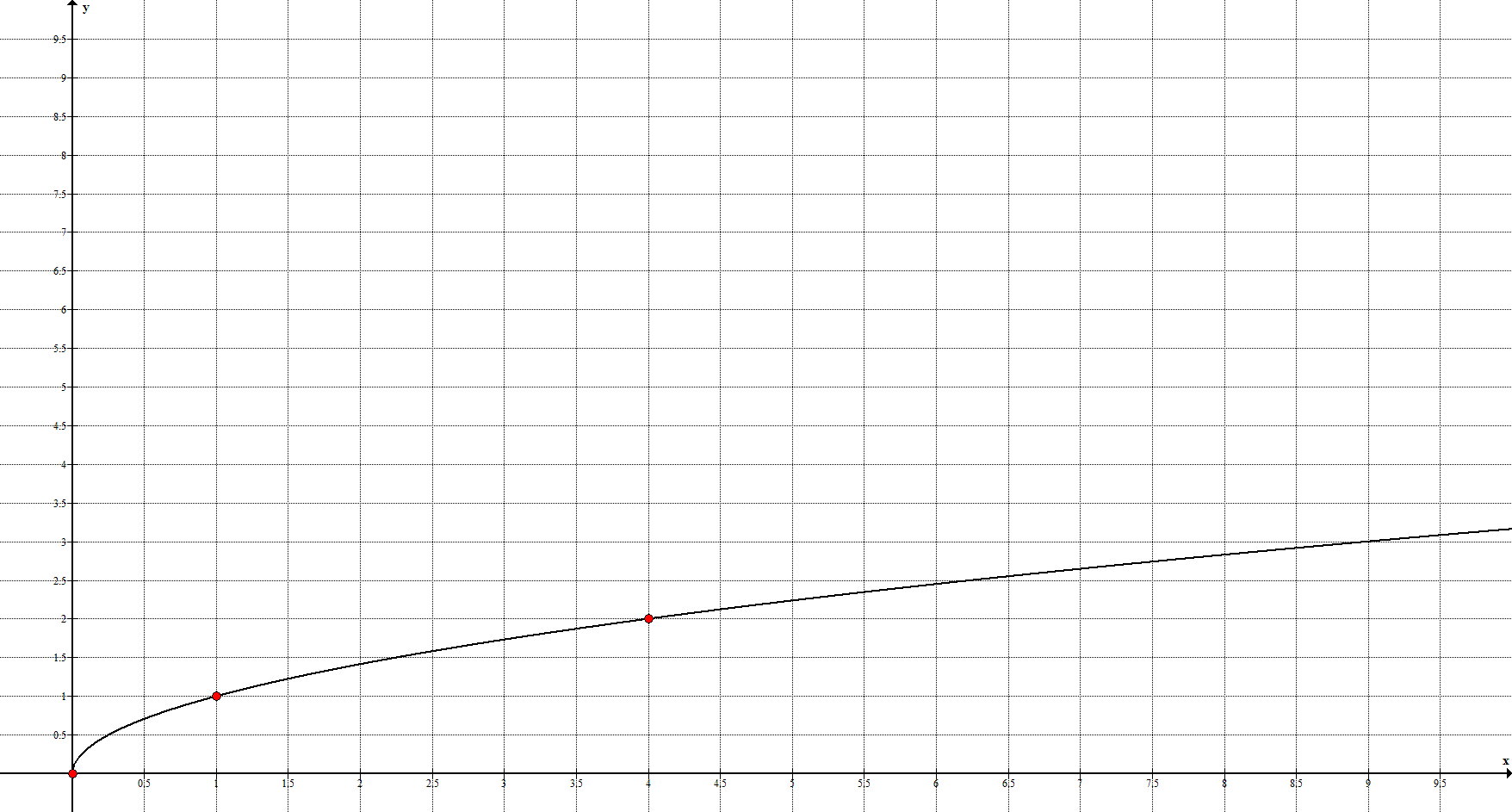
Ключевые точки: $(0;0), \ (1;1), \ (4;2)$
6. Показательная функция задаётся уравнением $y=a^
6*. Экспонента (показательная функция с основанием e) задаётся уравнением $y=e^
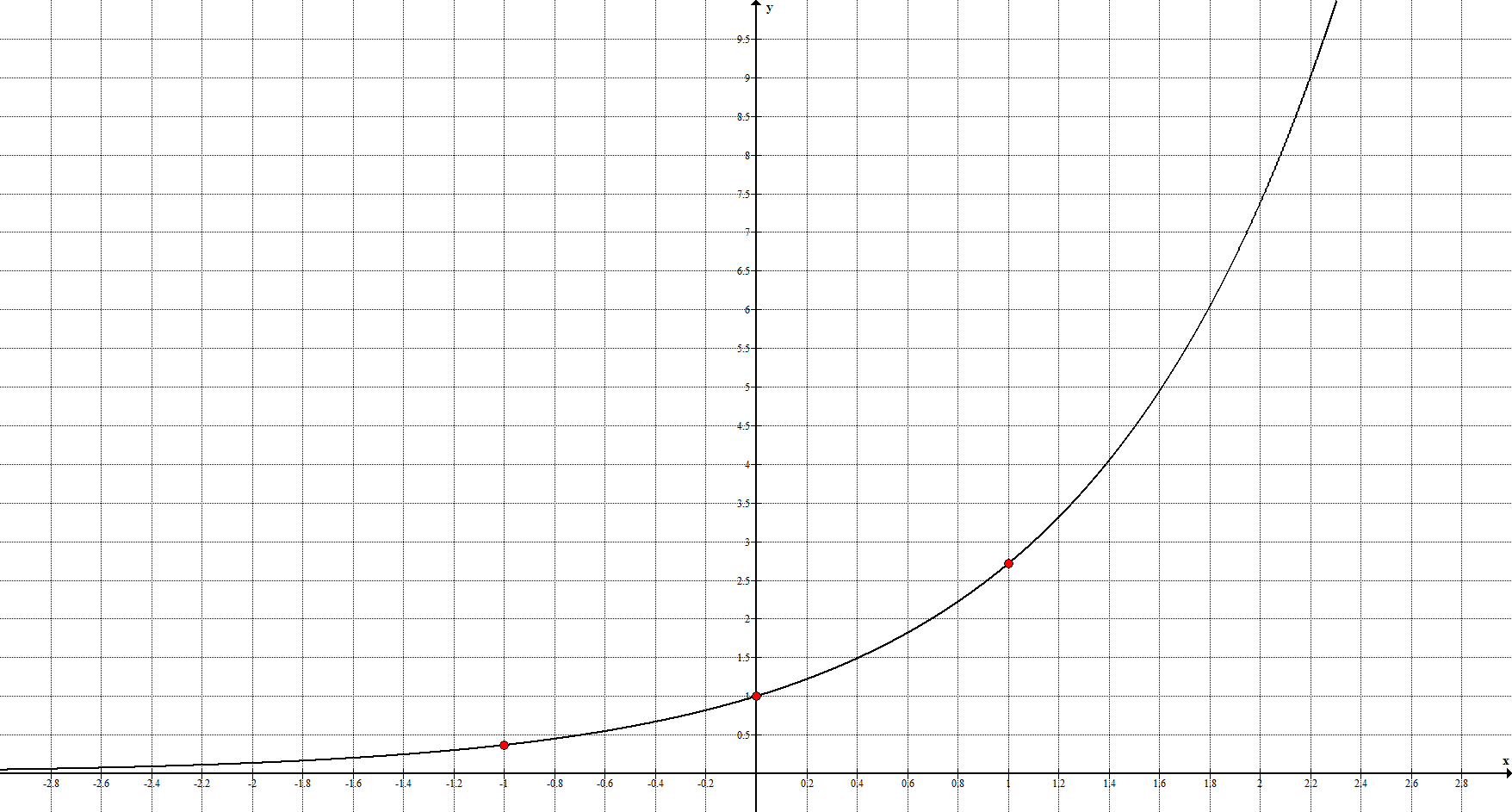
Ключевые точки: $\left(-1;\frac<1>
7. Логарифмическая функция задаётся уравнением $y=\log_
7*. Десятичный логарифм задаётся уравнением $y=\lg
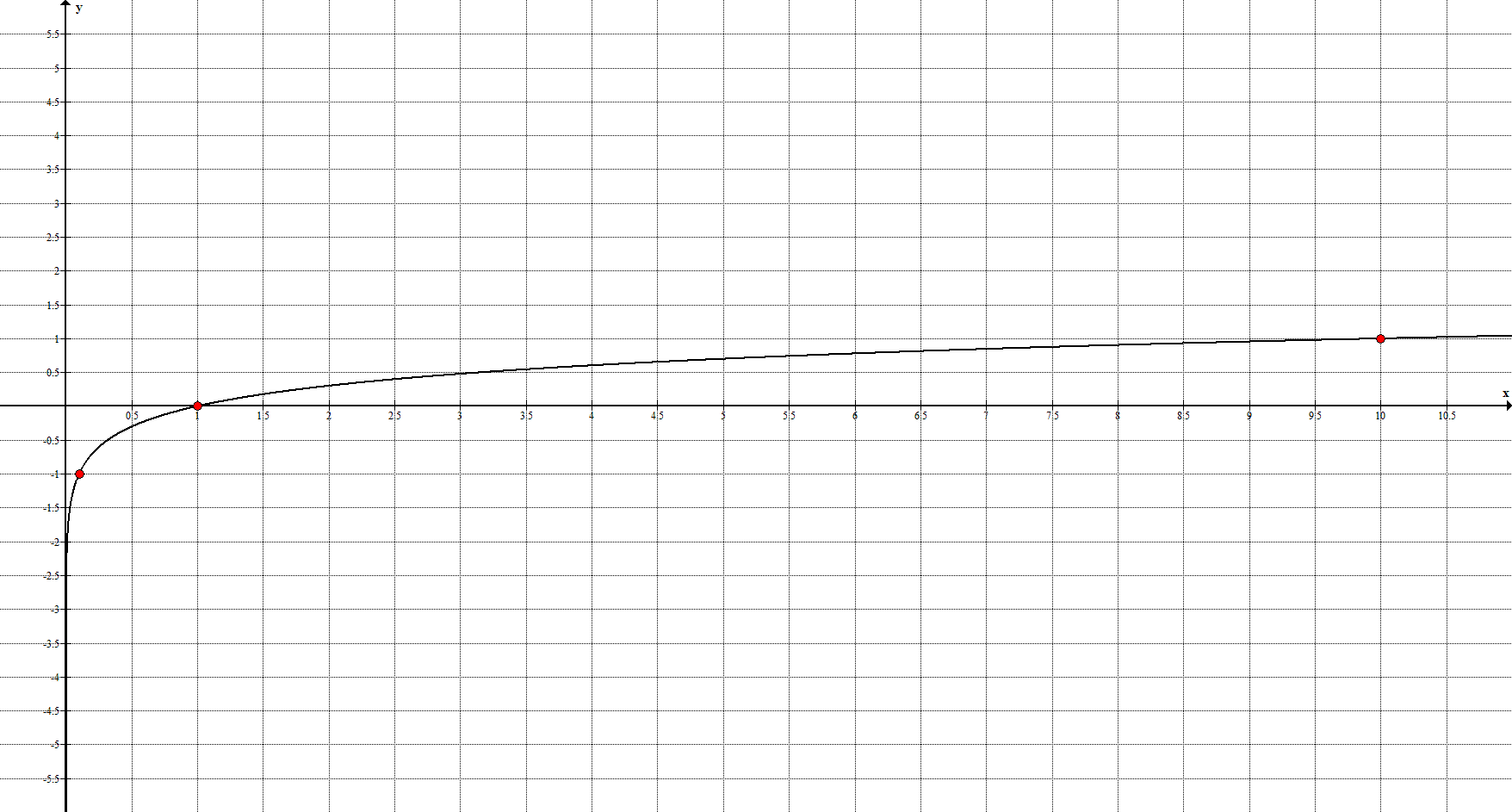
Ключевые точки: $(0,1; -1), \ (0;1), \ (10;1)$
7**. Натуральный логарифм задаётся уравнением $y=\ln
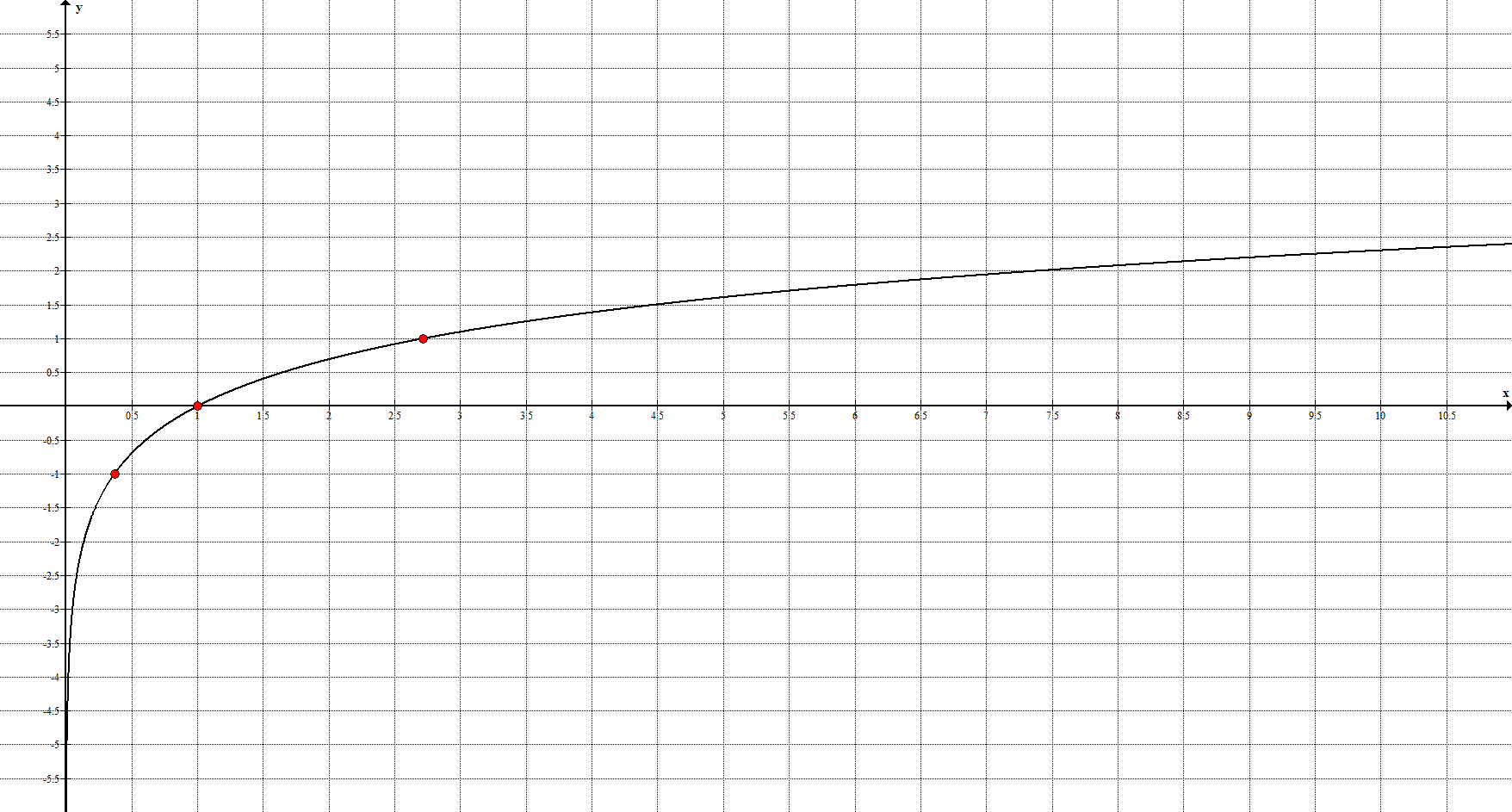
Ключевые точки: $\left(\frac<1>
8. Тригонометрические функции задаются уравнением $y=\sin
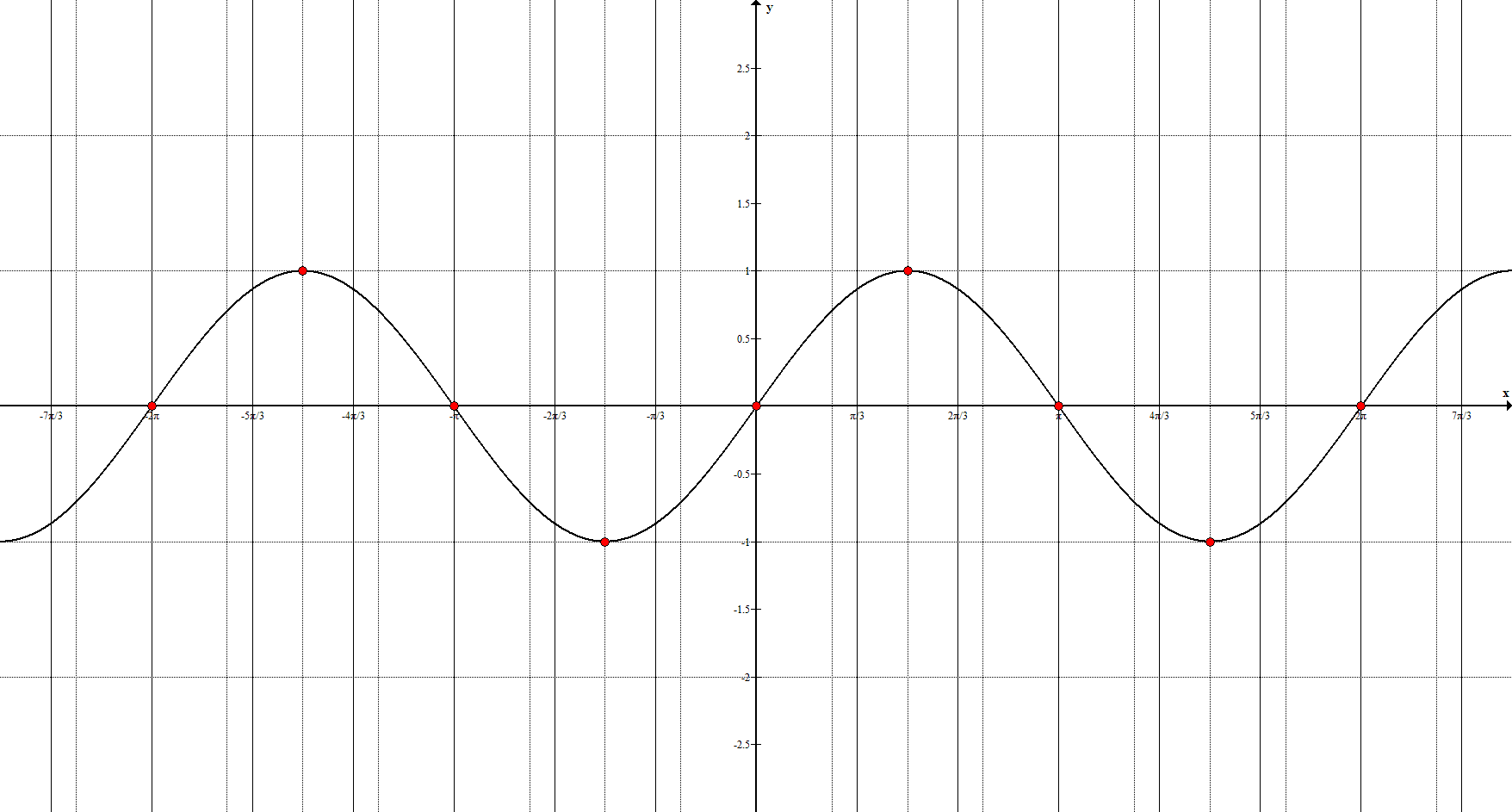
Синус
Ключевые точки: $(-2\pi; 0), \ \left(-\frac<3\pi><2>; 1\right), \ (-\pi;0), $
$\left(-\frac<\pi><2>; -1\right), \ (0;0), \ \left(\frac<\pi><2>; 1\right), \ (\pi; 0), \ \left(\frac<3\pi><2>; -1\right), \ (2\pi; 0)$
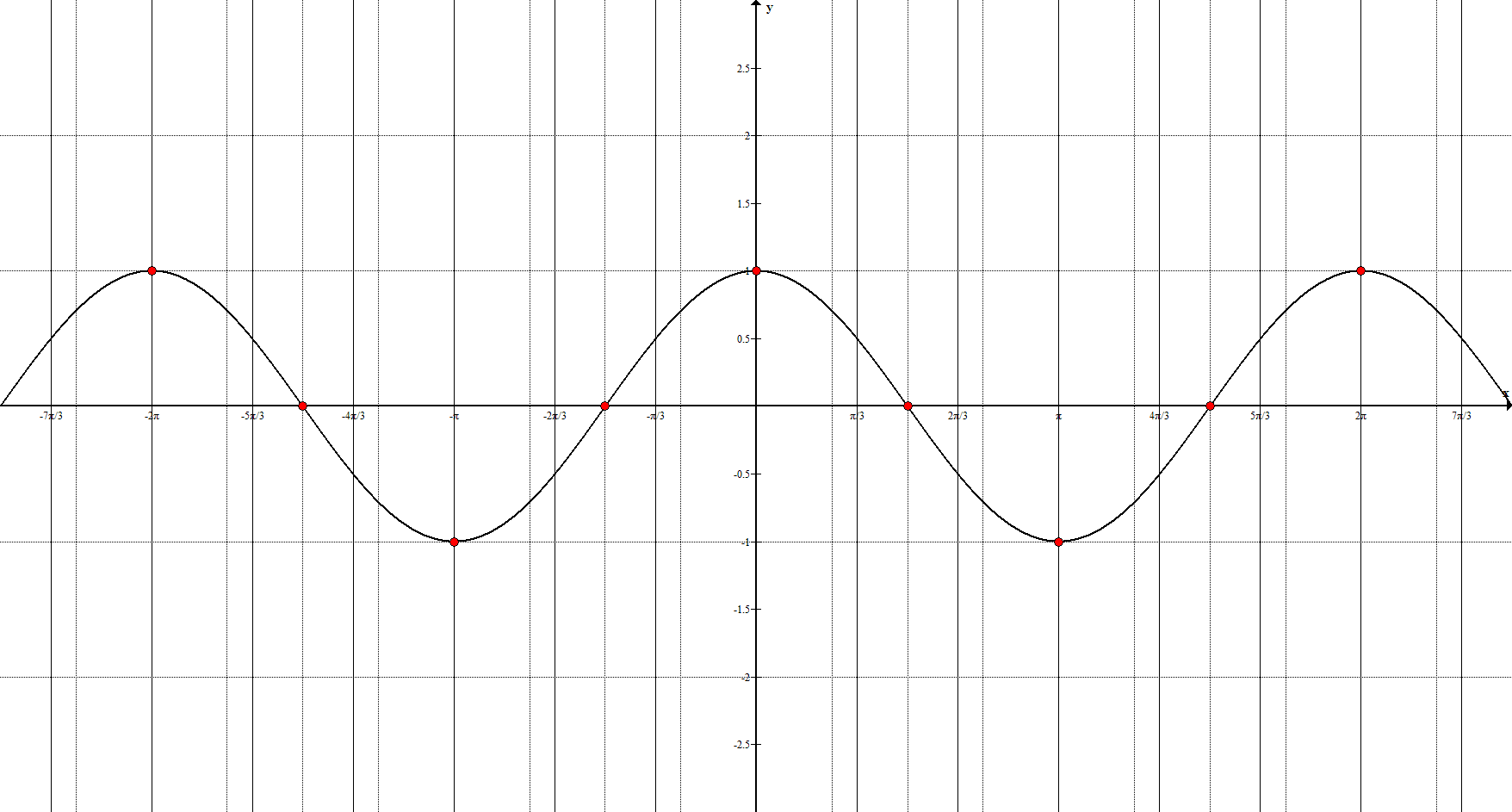
Косинус
Ключевые точки: $(-2\pi; 1), \ \left(-\frac<3\pi><2>; 0\right), \ (-\pi;-1), $
$\left(-\frac<\pi><2>; 0\right), \ (0;1), \ \left(\frac<\pi><2>; 0\right), \ (\pi;-1), \ \left(\frac<3\pi><2>; 0\right), \ (2\pi; 1)$
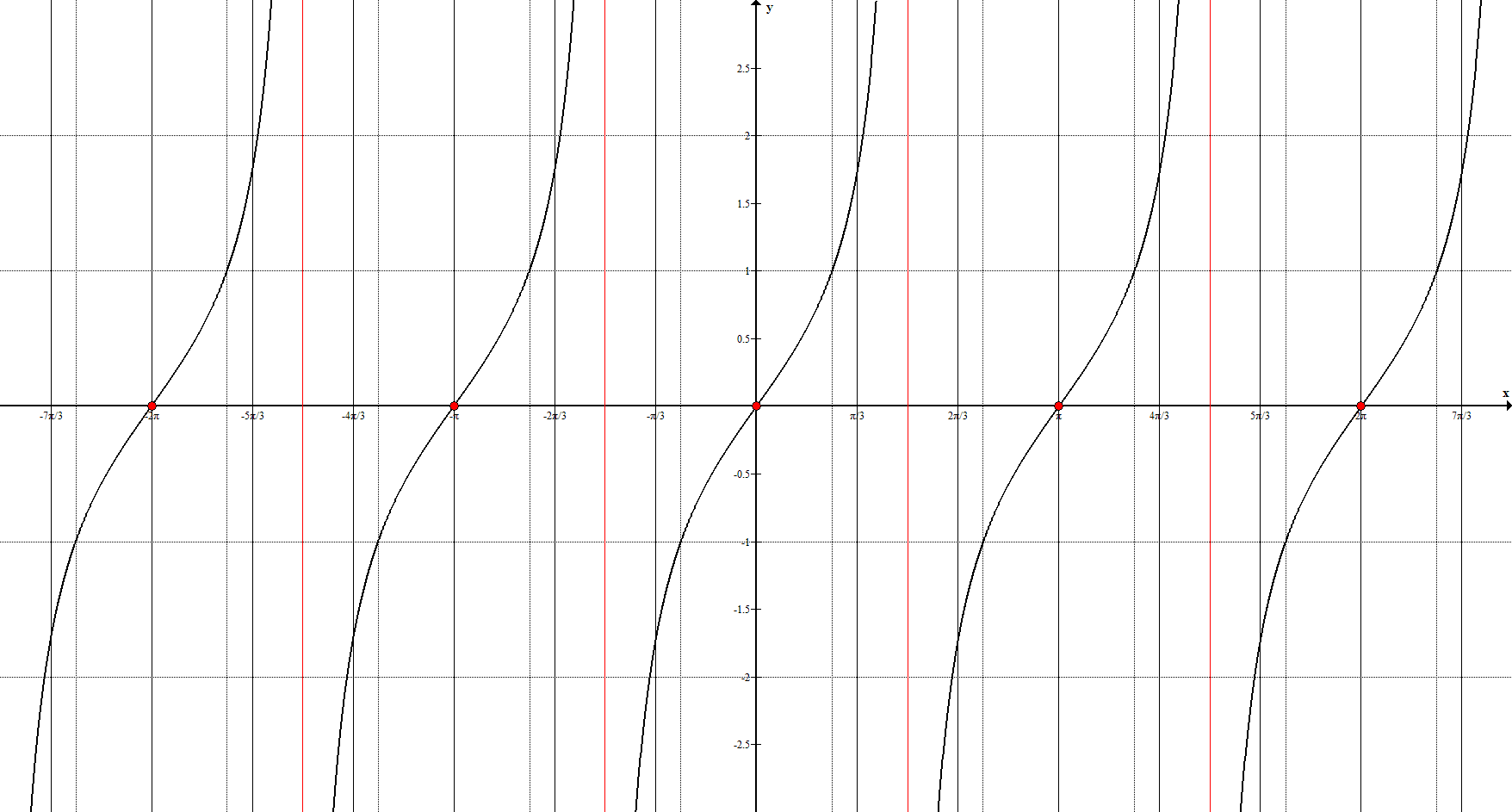
Тангенс
Асимптоты: $x=\frac<\pi><2>+\pi n, n \in Z$
Ключевые точки: $(-2\pi ;0), \ (-\pi ;0), \ (0;0), \ (\pi ;0), \ (2\pi ;0)$
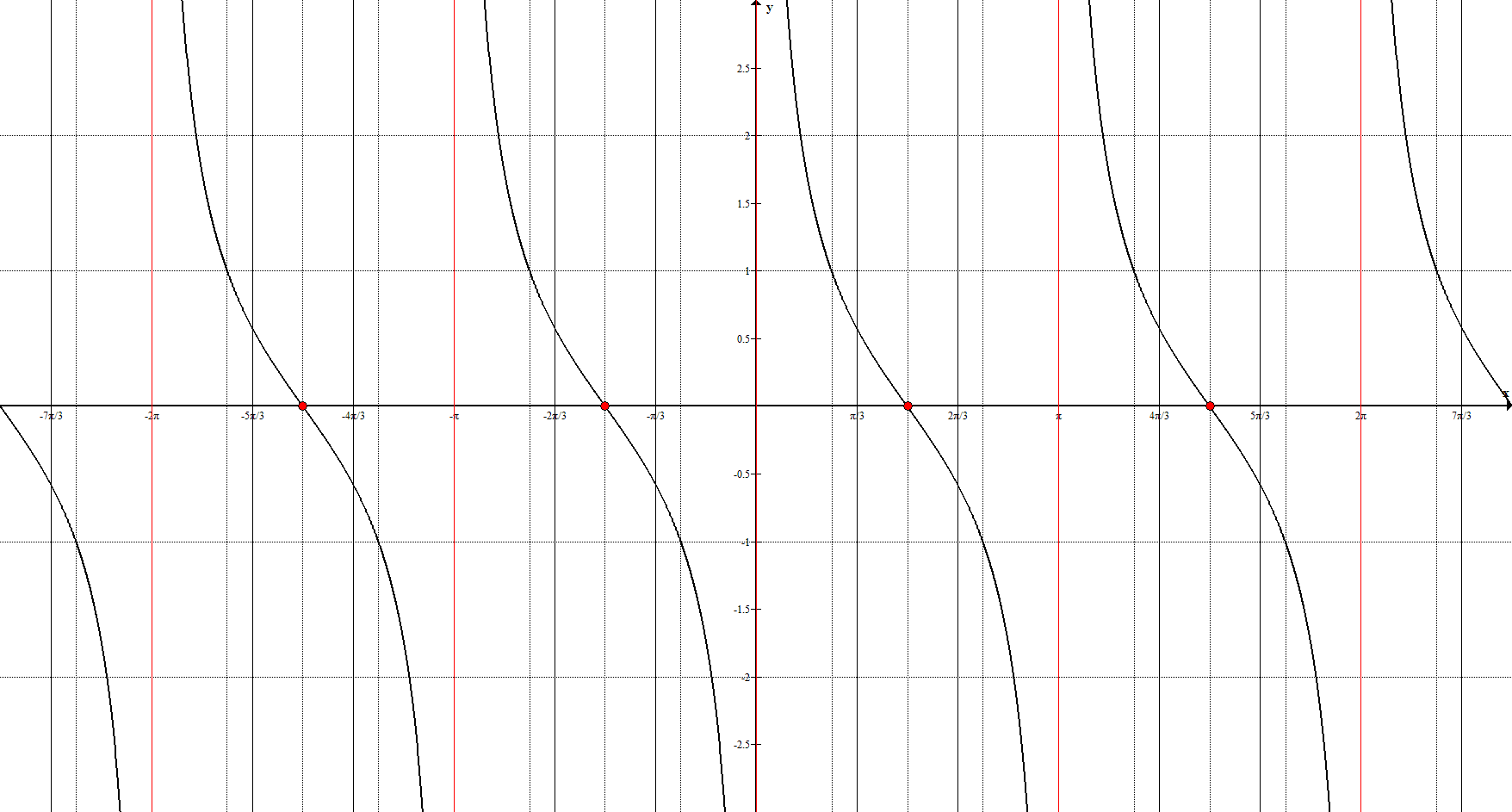
Котангенс
Асимптоты: $x=\pi n, n \in Z$
Ключевые точки: $\left(-\frac<3\pi><2>; 0\right), \ \left(-\frac<\pi><2>; 0\right), \ \left(\frac<\pi><2>; 0\right), \ \left(\frac<3\pi><2>; 0\right)$
9. Обратные тригонометрические функции задаются уравнением $y=\arcsin
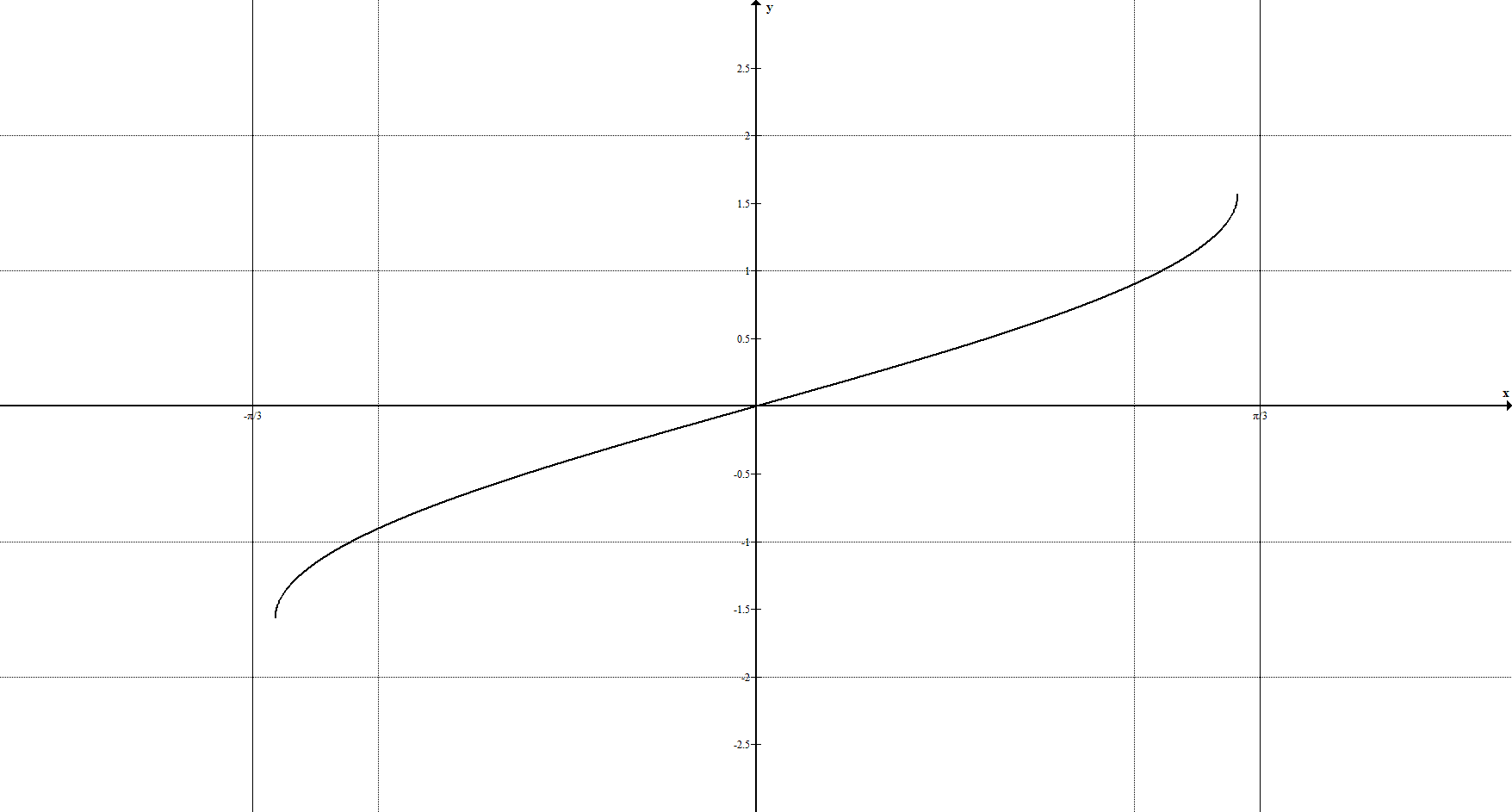
Арксинус 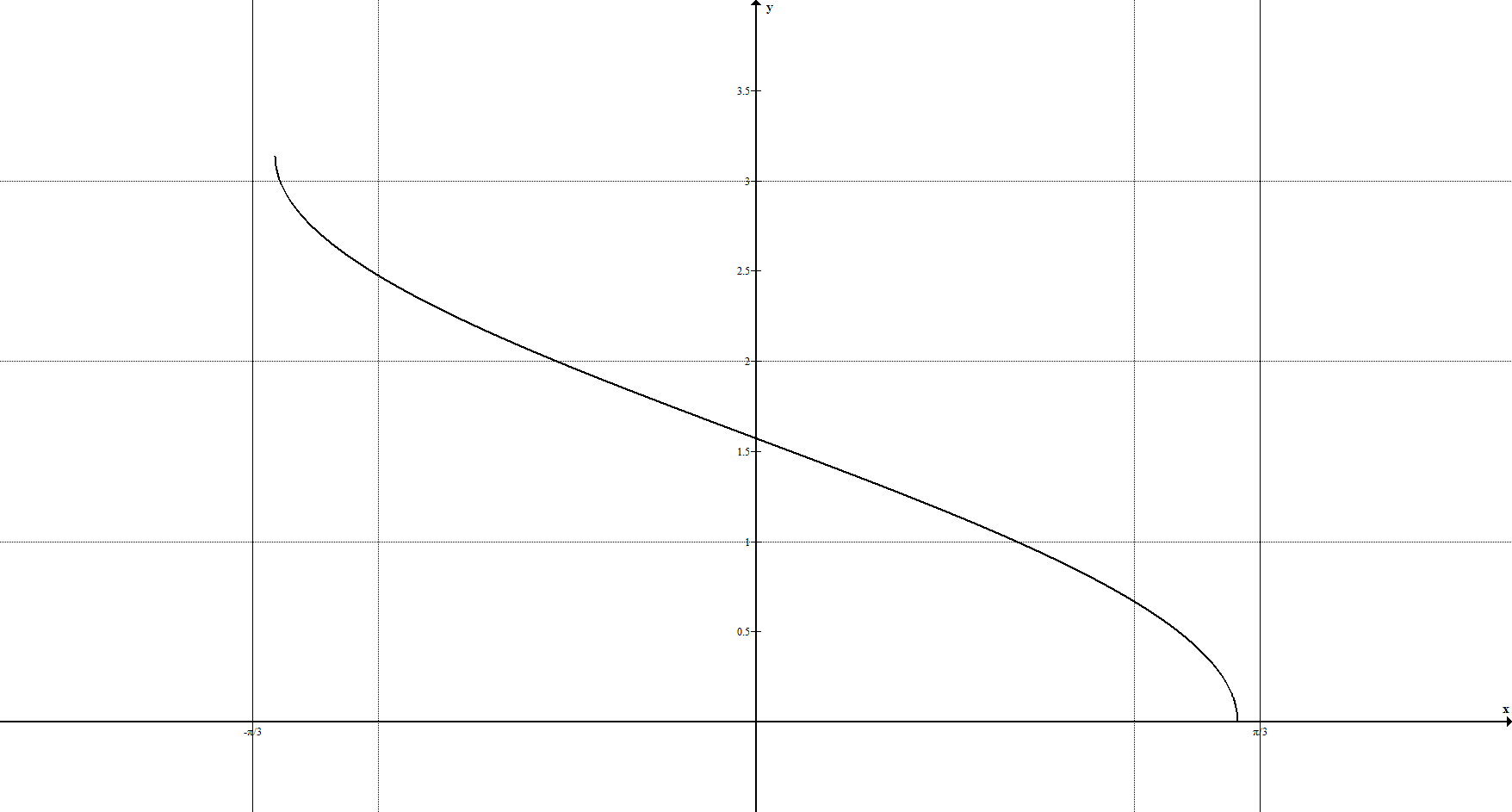
Арккосинус 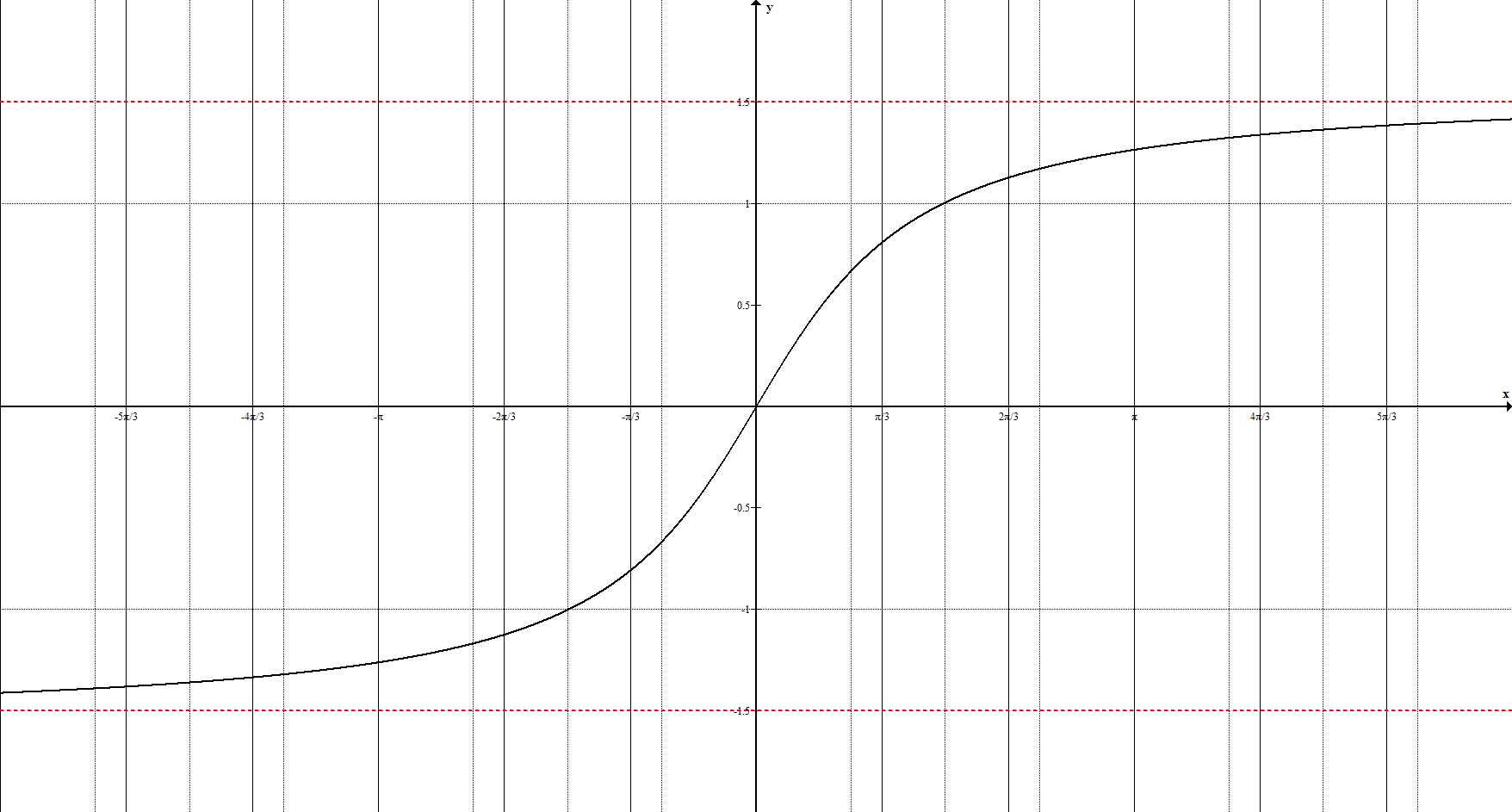
Арктангенс 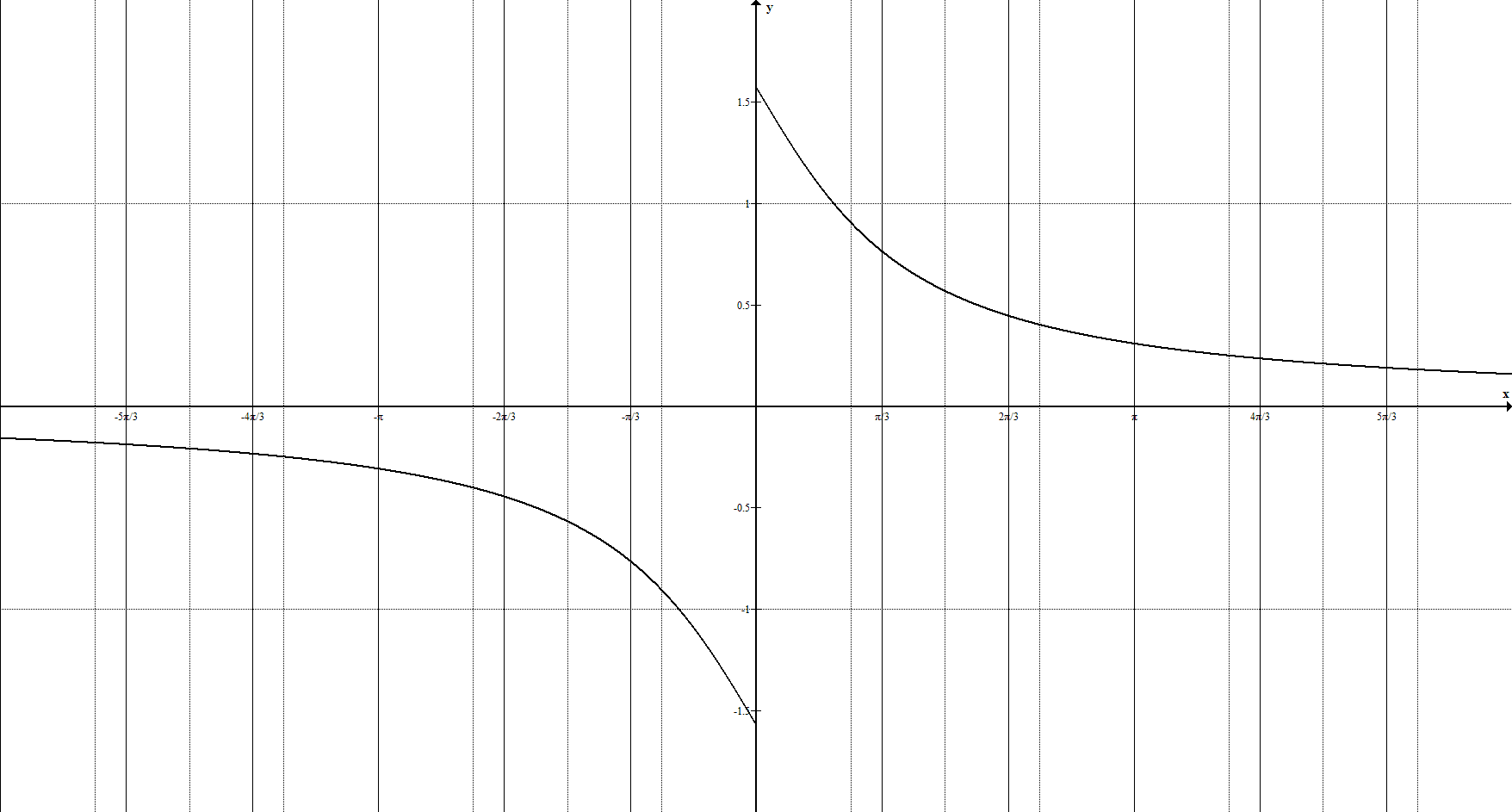
Арккотангенс
Методические материалы для подготовки к ЕГЭ по математике
Элементарные функции и их графики
Составила учитель математики
Коваленко И.Н.

















Выберите книгу со скидкой:

Математика. Сложение и вычитание. Уровень 3 Kumon
350 руб. 472.00 руб.

Математика. Готовлюсь к школе с наклейками
350 руб. 130.00 руб.

Математика. Новый полный справочник школьника для подготовки к ЕГЭ
350 руб. 222.00 руб.

СПЛОШНОЕ УЧЕНИЕ. ЗАНИМАТЕЛЬНАЯ МАТЕМАТИКА
350 руб. 204.00 руб.

Смешная математика (математика с наклейками)
350 руб. 56.00 руб.

Посчитаем, поиграем (математика с наклейками)
350 руб. 56.00 руб.

Математика до школы (математика с наклейками)
350 руб. 56.00 руб.

МОЯ РАБОЧАЯ ТЕТРАДЬ. ПЕРВАЯ МАТЕМАТИКА
350 руб. 35.00 руб.

Все формулы мира: Как математика объясняет законы природы
350 руб. 980.00 руб.

Математика космоса: Как современная наука расшифровывает Вселенную
350 руб. 860.00 руб.

350 руб. 116.00 руб.

Игра случая: математика и мифология совпадения
350 руб. 600.00 руб.
БОЛЕЕ 58 000 КНИГ И ШИРОКИЙ ВЫБОР КАНЦТОВАРОВ! ИНФОЛАВКА



- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы
- Коваленко Инна НиколаевнаНаписать 3967 04.06.2016
Номер материала: ДБ-110183
- Алгебра
- 11 класс
- Конспекты
Добавляйте авторские материалы и получите призы от Инфоурок
Еженедельный призовой фонд 100 000 Р
-
04.06.2016 6403
-
04.06.2016 1016
-
04.06.2016 357
-
04.06.2016 383
-
04.06.2016 332
-
04.06.2016 252
-
04.06.2016 442
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Элементарные функции и их графики
Прямая пропорциональность. Линейная функция.
Обратная пропорциональность. Гипербола.
Квадратичная функция. Квадратная парабола.
Степенная функция. Показательная функция.
Логарифмическая функция. Тригонометрические функции.
Обратные тригонометрические функции.
Пропорциональные величины. Если переменные y и x прямо пропорциона льны , то функциональная зависимость между ними выражается уравнением:
y = k x ,
где k - постоянная величина ( коэффициент пропорциональности ).
Линейная функция. Если переменные y и x связаны уравнением 1-ой степени:
A x + B y = C ,
где по крайней мере одно из чисел A или B не равно нулю, то графиком этой функциональной зависимости является прямая линия. Если C = 0, то она проходит через начало координат, в противном случае - нет. Графики линейных функций для различных комбинаций A , B , C показаны на рис.9.
Обратная пропорциональность. Если переменные y и x обратно пропорциональны , то функциональная зависимость между ними выражается уравнением:
y = k / x ,
где k - постоянная величина.
Основные характеристики и свойства гиперболы:
- функция монотонная ( убывающая ) при x 0 и при x > 0, но не
монотонная в целом из-за точки разрыва x = 0 ( подумайте, почему ? );
- функция неограниченная, разрывная в точке x = 0, нечётная, непериодическая;
- нулей функция не имеет.
Изобразите, пожалуйста, квадратную параболу для случая a > 0, D > 0 .
Основные характеристики и свойства квадратной параболы:
значений: … (ответьте, пожалуйста, на этот вопрос сами !);
- функция в целом не монотонна, но справа или слева от вершины
ведёт себя, как монотонная;
- функция неограниченная, всюду непрерывная, чётная при b = c = 0,
Показательная функция. Функция y = a x , где a - положительное постоянное число, называется показательной функцией. Аргумент x принимает любые действительные значения ; в качестве значений функции рассматриваются только положительные числа, так как иначе мы имеем многозначную функцию. Так, функция y = 81 x имеет при x = 1/4 четыре различных значения: y = 3, y = - 3, y = 3 i и y = - 3 i (проверьте, пожалуйста !). Но мы рассматриваем в качестве значения функции только y = 3. Графики показательной функции для a = 2 и a = 1/2 представлены на рис.17. Они проходят через точку ( 0, 1 ). При a = 1 мы имеем график прямой линии, параллельной оси Х, т. e . функция превращается в постоянную величину, равную 1. При a > 1 показательная функция возрастает, a при 0 a
область значений: y > 0 ;
- функция монотонна: возрастает при a > 1 и убывает при 0 a
- функция неограниченная, всюду непрерывная, непериодическая;
- нулей функция не имеет.
Логарифмическая функция. Функция y = log a x , где a – постоянное положительное число, не равное 1, называется логарифмической. Эта функция является обратной к показательной функции; её график ( рис.18 ) может быть получен поворотом графика показательной функции вокруг биссектрисы 1-го координатного угла.
Основные характеристики и свойства логарифмической функции:
- это монотонная функция: она возрастает при a > 1 и убывает при 0 a
- функция неограниченная, всюду непрерывная, непериодическая;
- у функции есть один ноль: x = 1.
Тригонометрические функции. При построении тригонометрических функций мы используем радианную меру измерения углов. Тогда функция y = sin x пред ставляется графиком ( рис.19 ). Эта кривая называется синусоидой.
Из этих графиков очевидны характеристики и свойства этих функций:
имеющие так называемые интервалы монотонности , внутри которых они
ведут себя, как монотонные функции ( см. графики рис.19 и рис.20 );
Графики функций y = tan x и y = cot x показаны соответственно на рис.21 и рис .22
Функции y = arcsin x и y = arccos x обладают следующими характеристиками и свойствами:
- функции ограниченные, непериодические, непрерывные и монотонные
( y = arcsin x – возрастающая функция; y = arccos x – убывающая );
- каждая функция имеет по одному нулю ( x = 0 у функции y = arcsin x и
x = 1 у функции y = arccos x ).
Функции y = arctan x и y = arccot x имеют следующие характеристики и свойства:
- функции ограниченные, непериодические, непрерывные и монотонные
( y = arctan x – возрастающая функция; y = arccot x – убывающая );
- только функция y = arctan x имеет единственный ноль ( x = 0 );
функция y = arccot x нулей не имеет.
Читайте также:


