Отношения между понятиями шпора
§ 5. Логические отношения между понятиями
Так как все предметы находятся во взаимодействии и взаимообусловленности, то и понятия, отражающие данные предметы, также находятся в определенных отношениях. Конкретные виды отношений устанавливаются в зависимости от содержания и объема понятий, которые сравниваются.
В логических отношениях могут находиться только сравнимые понятия. В зависимости от того, как соотносятся их объемы, понятия делятся на две группы: совместимые и несовместимые.
Совместимые - это такие понятия, объемы которых совпадают полностью или частично. Несовместимые - это понятия, объемы которых не совпадают ни в одном элементе, но которые могут быть включены частично или полностью в объем общего для них понятия. На представленной схеме показаны виды совместимых и несовместимых понятий.

Отношения между понятиями принято иллюстрировать при помощи кругов Эйлера (круговых схем), названных так в честь Леонардо Эйлера (1707-1783) - одного из крупнейших математиков XVIII века, родившегося в Швейцарии, но весь свой талант отдавшего России. Каждый круг обозначает объем понятия, а любая точка внутри круга - предмет, входящий в его объем. Круговые схемы позволяют наглядно представить отношения между различными понятиями, лучше осмыслить и усвоить эти отношения.
Рассмотрим совместимые понятия.
В отношениях равнозначности находятся совместимые понятия, объемы которых полностью совпадают. В таких понятиях мыслится один и тот же предмет или класс однородных предметов. Однако содержание этих понятий различно, так как каждое из них отражает только определенную сторону (существенный признак) данного предмета или класса однородных предметов.

В отношении пересечения находятся совместимые понятия, у которых объемы частично совпадают. Частично совпадает и содержание данных понятий.

В отношении подчинения находятся совместимые понятия, объем одного из которых полностью входит в объем другого, составляя его часть.

Объем первого понятия шире объема второго понятия: кроме кражи личного имущества граждан в него входит также кража государственного, кооперативного имущества.
Из двух понятий, находящихся в отношении подчинения, понятие с большим объемом (подчиняющее) является родовым, или родом по отношению к понятию с меньшим объемом (подчиненному), а последнее по отношению к первому называется видовым, или видом. Родовидовые отношения лежат в основе логических операций ограничения и обобщения понятий, деления объема понятий и некоторых видов определения.
Перейдем к рассмотрению несовместимых понятий.
При иллюстрации отношений между несовместимыми понятиями возникает потребность во введении более широкого по объему понятия, которое включало бы объемы несовместимых понятий.
В отношении соподчинения находятся два или более непересекающихся понятий, принадлежащих общему родовому понятию.


В отношении противоположности находятся понятия, которые являются видами одного и того же рода, и при этом одно из них содержит какие-то признаки, а другое эти признаки отрицает и заменяет противоположными признаками.

В отношении противоречия находятся такие два понятия, которые являются видами одного и того же рода, и при этом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, исключает, не заменяя их никакими другими признаками.
Таким образом, уяснение логической структуры понятий, определение их видов и отношений между сравнимыми понятиями дает возможность перейти к рассмотрению логических действий, или операций над понятиями.
Вот эти категории:
1. Субстанция (substantia).
2. Количество (quantitas).
3. Качество (qualitas).
4. Отношение (relatio).
5. Место (ubi).
6. Время (quando).
7. Положение (situs).
8. Обладание (habitus).
9. Действие (actio).
10. Страдание (passio).
Под эти десять категорий, по мнению Аристотеля, подходит всё то, что можно мыслить. Если мы желаем высказать о тех или других вещах что-либо самое общее, то мы не можем о них высказать ничего другого, кроме того, что они суть или субстанции, или что они обозначают качество, отношение, место и т.п. Других точек зрения, кроме тех, которые содержатся в категориях, не существует. Таким образом, можно сказать, что категории представляют собой наиболее общие классы всего мыслимого.
В новейшей философии в качестве наиболее общих классов мыслимого философы различают вещь, свойство, отношение. Всё, о чём мы можем мыслить, есть или вещь (субстанция), или это есть свойство (атрибут), или, наконец, это есть отношение.
Под вещами мы понимаем то, что обладает большим или меньшим постоянством формы. Например, таким постоянством обладают камень, дерево, жидкость в сосуде и т.п. Кусок камня сегодня обладает той же формой, какой он обладал вчера: нам представляется, что такое постоянство будет ему присуще и впоследствии.
Вещи мы представляем или имеющими известные свойства или качества, или совершающими известные действия, или находящимися в известном состоянии. Например, то, что кусок железа имеет известную тяжесть, есть его свойство, или качество. Если кусок железа накалён, то это есть его состояние: если кусок железа плавится или движется, то это есть известный процесс, состояние. Свойства, действия, состояния мы представляем принадлежащими известной вещи как известной носительнице их. Но в то же время мы их мыслим как элементы, из которых состоит вещь: мы мыслим железо как нечто, имеющее известную тяжесть, твёрдость, способность накаляться, приходить в движение и т.п. Качество, действие, состояние мы будем называть одним общим именем – свойства вещи.
Одна вещь может мыслиться нами находящейся в различных отношениях к другой вещи. Одна вещь может быть больше, чем другая (пространственное отношение); одна вещь может быть причиной другой вещи (причинное отношение); одна вещь может возникнуть раньше, чем другая (временное отношение), и т.п.
Всё, что мы можем мыслить, мы должны мыслить под одной из этих категорий, т.е. всё, что мы мыслим, мы должны мыслить или как вещь, или как свойство вещи, или как отношение. Эти три наиболее общих понятия мы и считаем категориями.
Этим исчерпывается вопрос о категориях.
Отношения между понятиями. Рассмотрим логические отношения, существующие между понятиями.
4. Противные и противоречащие понятия. На эти два различных класса понятий, очень сходных по своим внешним свойствам, но в то же время совершенно различных по существу, следует обратить особенное внимание и хорошенько продумать их различие, так как при оперировании с ними легко впасть в ошибку.
Кругом символизируется какое-нибудь одно понятие A, и вне его ставится другое понятие B, которое есть не-A, причём это понятие B может быть поставлено где угодно, лишь бы не внутри круга, не в его объёме; это второе понятие по своим свойствам называется понятием отрицательным или неопределённым (notio negativa seu indefinita).
Что такое категория? Какие категории признавал Аристотель? Какие следует признавать категории? Что такое вещь, свойство, отношение? Что такое подчинение понятий? Приведите примеры. Что такое соподчинение понятий? Приведите примеры. Какие понятия называются равнозначащими? Приведите примеры. Какие понятия называются противными или противоположными? Приведите примеры. Какие понятия называются противоречащими? Приведите примеры. Что такое скрещивающиеся понятия? Приведите примеры. Какие понятия несравнимые? Что необходимо для того, чтобы понятая можно было сравнивать?

А мы продолжаем:
Все вещи, явления объективного мира находятся во всеобщей связи и взаимозависимости. И наши понятия являясь отражением объективного мира, находятся во взаимной связи друг с другом, в том или ином отношении друг к другу.
Такие понятия, которые по своему содержанию находятся в далёком отношении друг к другу, называются несравнимыми понятиями.
Все остальные понятия являются сравнимыми. Они делятся на две группы:
1) совместимые понятия и
2) несовместимые понятия.
Если объёмы двух (или более) понятий совпадают полностью или частично, то это будут совместимые понятия, если же не совпадают, то это будут несовместимые понятия.
Заметим, что в том и другом случае имеются в виду объёмы понятий, следовательно, отношения между понятиями, которые будут рассматриваться далее, — это отношения по объёму.
Рассмотрим группу совместимых понятий.
ОТНОШЕНИЕ ТОЖДЕСТВА. Есть понятия, которые могут различаться по своему содержанию, но в которых мыслится один и тот же предмет. Такие понятия находятся в отношении тождества.
ОТНОШЕНИЕ ПОДЧИНЕНИЯ. При отношении подчинения одно понятие (менее общее) входит в объём другого понятия (более общего).
Более общее (родовое) понятие называется подчиняющим, а менее общее (видовое) называется подчинённым понятием.
Отношение подчинения понятий не следует смешивать с отношением части и целого.
Такие понятия, объёмы которых частично совпадают, называются перекрещивающимися понятиями.
Между несовместимыми понятиями также существуют три вида отношений:
ОТНОШЕНИЕ СОПОДЧИНЕНИЯ. Когда одному и тому же родовому понятию подчинены несколько видовых понятий, то эти видовые понятия находятся между собой в отношении соподчинения.
Отношение соподчинения есть отношение между видами, объединёнными общим родом.
Объёмы соподчинённых понятий не совпадают друг с другом, но все они входят в объём одного и того же родового понятия.
ОТНОШЕНИЕ ПРОТИВОПОЛОЖНОСТИ. В отношении противоположности находятся такие два понятия, которые по своему содержанию противоположны друг другу, но оба входят в объём одного и того же родового понятия.
Каждое из противоположных понятий не только отрицает своим содержанием другое, противоположное понятие, но и утверждает взамен другого, противоположного, нечто новое, несовместимое с ним.
![]()
Книга друг человека

![]()
Вот читаешь серьезные книжки, а там.

![]()
Как Обучается Искусственный Интеллект
Как все алгоритмы вокруг нас учатся выполнять свою работу?
Сриниваса Рамануджан Айенгор - друг чисел.

Привет,Пикабу! Сегодня я хотел бы рассказать историю одного удивительнейшего ученого XX века - Рамануджана. Удивительна она потому, что этот человек смог добиться огромных результатов в области теории чисел и математического анализа, не имея при этом высшего образования, пройдя путь из простого бухгалтера в одного из талантливейших математиков того времени.
Рамануджан Сриниваса родился 22 декабря 1887 года Ченнаи, Мадрасское президентство, на юге Индии, в тамильской семье, принадлежал Рамануджан к каста брахманов.
В 1913 году известный профессор Кембриджского университета Годфри Харди получил письмо от Рамануджана, в котором Рамануджан сообщал, что он не заканчивал университета, а после средней школы занимается математикой самостоятельно. К письму были приложены формулы, автор просил их опубликовать, если они интересны, поскольку сам он беден и не имеет для публикации достаточных средств. Между кембриджским профессором и индийским клерком завязалась оживленная переписка, в результате которой у Харди накопилось около 120 формул, не известных науке. По настоянию Харди в 27-летнем возрасте Рамануджан переехал в Кембридж. Там он стал профессором университета, его выбрали в Лондонское королевское общество. Печатные труды с его формулами выходили один за другим, вызывая удивление, а подчас и недоумение коллег.
Годфри Харди:

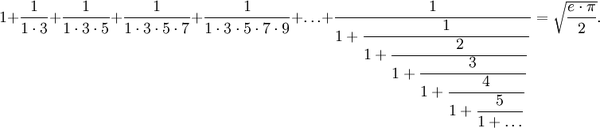
Математикам хорошо известна формула вычисления числа pi , полученная Рамануджаном в 1910 году путём разложения арктангенса в ряд Тейлора:
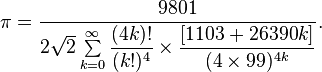
Но самой известной его работой, совместная с профессором Харди, является работа по асимптотике разбиения натуральных чисел. То есть представление какого-либо натурального числа N в виде суммы других натуральных чисел.
Например, <3,1,1>или <3,2>— разбиения числа 5, поскольку 5 = 3 + 1 + 1 = 3 + 2. Всего существует p(5) = 7 разбиений числа 5: <1,1,1,1,1>, <2,1,1,1>, <2,2,1>, <3,1,1>, <3,2>, <4,1>, <5>.
Формула Харди-Рамануджана:
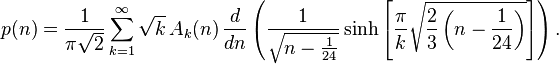
Сфера его математических интересов была очень широка. Это магические квадраты, квадратура круга, бесконечные ряды, гладкие числа, разбиения чисел, гипергеометрические функции, специальные суммы и функции, ныне носящие его имя, определённые интегралы, эллиптические и модулярные функции. + множество формул,теорем и равенств в теории чисел.
Сам Рамануджан говорил, что формулы ему во сне внушает богиня Намагири Тхайяр.
Умер в Мадрасском президентстве вскоре после возвращения в Индию. Причиной ранней (в возрасте 32 лет) смерти мог быть туберкулёз, усугубленный последствиями недоедания, истощения и стресса.
Предметы мира находятся друг с другом во взаимосвязи и взаимообусловленности. Поэтому и понятия, отражающие эти предметы, также находятся в определенных отношениях. Далекие друг от друга по своему содержанию понятия, не имеющие общих признаков, называются несравнимыми (например, “поэма” и “колодец”; “невоспитанность” и “радуга”), остальные понятия называются сравнимыми.
Совместимые понятия могут быть в отношениях равнозначности, пересечения и подчинения.


Отношениями равнозначности, пересечения и подчинения исчерпываются все случаи совместимости между понятиями.
Несовместимые понятия могут быть в отношениях соподчинения, противоположности и противоречия.
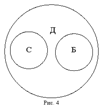
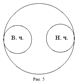

Отношениями соподчинения, противоположности и противоречия исчерпываются все случаи несовместимости между понятиями.
Итак, в логике выделяется шесть вариантов отношений между понятиями. Для удобства их запоминания они представлены в табл. 2.

Как нам уже известно, отношения между понятиями изображаются круговыми схемами Эйлера. Причём до сих пор мы изображали схематично отношения между двумя понятиями, но это можно сделать и с большим числом понятий.


Указанные четыре понятия находятся в отношении последовательного подчинения: дедушка – это обязательно отец, а отец – не обязательно дедушка; любой отец – это обязательно мужчина, однако не всякий мужчина является отцом; наконец, мужчина – это обязательно человек, но человеком может быть не только мужчина.

Попробуйте самостоятельно прокомментировать эту схему, установив все имеющиеся на ней виды отношений между понятиями.
Определите отношения между понятиями
1. Игрушка, заводная игрушка, кукла, заводной автомобиль, пистолет

2. Стихийное бедствие, землетрясение, явление природы, наводнение, гроза
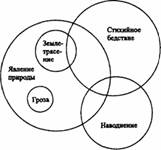
Подытоживая всё сказанное, отметим, что отношения между понятиями – это отношения между их объёмами. Значит, для того чтобы можно было установить отношения между понятиями, их объём должен быть резким, а содержание, соответственно, ясным, т. е. эти понятия должны быть определёнными.
Проверьте себя:
1. Какие понятия называются в логике совместимыми, а какие – несовместимыми? Приведите по пять примеров совместимых и несовместимых понятий.
2. В каких отношениях могут быть совместимые понятия? Что представляют собой отношения равнозначности, пересечения и подчинения между понятиями? Что такое видовые и родовые понятия?
3. В каких отношениях могут быть несовместимые понятия? Что представляют собой отношения соподчинения, противоположности и противоречия между понятиями? Чем отличается противоположность от соподчинения и противоречие от противоположности?
4. Каким образом изображаются отношения между понятиями?
5. В каком отношении находятся понятия, обозначающие часть и целое? Почему между этими понятиями не может быть отношения подчинения?
6. Определите, в каких отношениях находятся следующие понятия:
двоечник и студент,
композитор и человек,
город и деревня,
треугольник и сторона треугольника,
школа №5 и учебное заведение,
знаменитый человек и немецкий писатель,
дом и крыша дома,
собака и кошка,
умный человек и неумный человек,
физика и химия,
столица и населённый пункт,
книга и интересная книга,
телевизор и планета солнечной системы,
растение и крапива,
окружность и круг,
Николай II и последний русский царь,
олимпийские игры и спортивные состязания.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Так как все предметы находятся во взаимодействии и взаимообусловленности, то и понятия, отражающие данные предметы, также находятся в определённых отношениях. Конкретные виды отношений устанавливаются в зависимости от содержания и объёма понятий.
По содержанию могут быть два вида отношений между понятиями – сравнимость и несравнимость.
В логических отношениях могут находиться только сравнимые понятия. Логический анализ несравнимых понятий невозможен.
В зависимости от того, как соотносятся объёмы сравнимых понятий, понятия делятся на две группы: совместимые и несовместимые.
Совместимые– это такие понятия, объёмы которых совпадают полностью или частично.Несовместимые – это понятия, объёмы которых не совпадают ни в одном элементе, но которые могут быть включены частично или полностью в объём общего для них понятия. Отношения между понятиями разделяются на отношения совместимости и несовместимости.
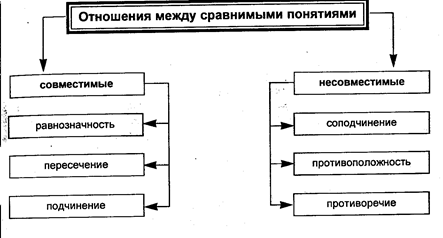
Отношения между понятиями принято иллюстрировать при помощи кругов Эйлера (круговых схем), названных так в честь Леонарда Эйлера (1707 – 1783) – одного из крупнейших математиков XVIII века, родившегося в Швейцарии, но весь свой талант отдавшего России. Каждый круг обозначает объём понятия, а любая точка внутри круга – предмет, входящий в его объём. Круговые схемы позволяют наглядно представить отношения между различными понятиями, лучше осмыслить и усвоить эти отношения.
Типы отношений совместимости понятий:
1). В отношенияхравнозначности (тождественности) находятся совместимые понятия, объёмы которых полностью совпадают. В таких понятиях мыслится один и тот же предмет или класс однородных предметов. Однако содержание этих понятий различно, так как каждое из них отражает только определённую сторону (существенный признак) данного предмета или класса однородных предметов.
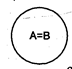
2). В отношенииподчинения (субординации) находятся совместимые понятия, объём одного из которых полностью входит в объём другого, составляя его часть, не исчерпывая всего его содержания.

Объём первого понятия шире объёма второго понятия: кроме кражи личного имущества граждан в него входит также кража государственного, кооперативного имущества; есть другие металлы, кроме золота; берёза – один из видов деревьев.
Предельно общие понятия являются только родовыми, единичные понятия – только видовыми, остальные могут быть и теми, и другими. Родовидовые отношения лежат в основе логических операций ограничения и обобщения понятий, деления объёма понятий и некоторых видов определения.
3). В отношениипересечения (перекрещивания) находятся совместимые понятия, у которых объёмы частично совпадают. Частично совпадает и содержание данных понятий.

При иллюстрации отношений междунесовместимыми понятиями возникает потребность во введении более широкого по объёму понятия, которое включало бы объёмы несовместимых понятий.
Типы отношений несовместимости понятий:
1). В отношении соподчинения (координации) находятся два или более непересекающихся понятий, принадлежащих общему родовому понятию.
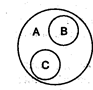
2). В отношениипротивоположности (контрарности) находятся понятия, которые являются видами одного и того же рода, и при этом содержат взаимоисключающие признаки.

3). В отношениипротиворечия (контрадикторности) находятся такие два понятия, которые являются видами одного и того же рода, и при этом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, исключает, не заменяя их никакими другими признаками.

Итак, в логике выделяется шесть вариантов отношений между понятиями. Любые два сравнимых понятия обязательно находятся в одном из шести указанных случаев отношений.
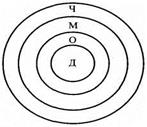
Как видим, указанные четыре понятия находятся в отношении последовательного подчинения: дедушка – это обязательно отец, а отец – не обязательно дедушка; любой отец – это обязательно мужчина, однако не всякий мужчина является отцом; и, наконец, мужчина – это обязательно человек, но человеком может быть не только мужчина.

Знание отношений между понятиями имеет огромное значение для их правильного употребления в устной и письменной речи, отражения действительных отношений между самими вещями, обозначаемыми понятиями. Содержание равнозначных понятий может меняться (от негативной оценки к нейтральной или положительной, и наоборот). Один и тот же человек может обозначаться по-разному: фамилия (Петров), местоимение (он), социальный статус (студент), ситуация (потерпевший).
Логические ошибки в отношениях между понятиями:
1) использование неравнозначных понятий в качестве равнозначных: плебисцит (опрос общественного мнения) и референдум (опрос, имеющий юридическую силу) – одинаковы по процедуре проведения;
Таким образом, уяснение логической структуры понятий, определение их видов и отношений между сравнимыми понятиями даёт возможность перейти к рассмотрению логических действий, или операций над понятиями.

Скорее всего, немногие люди задумываются над тем, что они мыслят и рассуждают с помощью понятий. Понятия подобны воздуху: мы их не замечаем, но при этом не можем без них размышлять. Каждый ребёнок естественно научается думать с их помощью в семь-восемь лет, переходя от оперирования с конкретными предметами к оперированию с идеями. Тем не менее, это не означает, что каждый умеет правильно ими пользоваться, а ведь без этого умения путь к логичному рассуждению закрыт. Вот почему в этом уроке, мы расскажем, что такое понятия, какие бывают виды понятий, как разные понятия соотносятся друг с другом и как с ними правильно обращаться.
Содержание
Что такое понятие?
С точки зрения логики, понимать слово означает быть в состоянии указать, какие именно предметы им обозначаются, то есть уметь устанавливать относительно любого предмета, можно ли его назвать данным словом или нет. Каким образом этого достичь? Через образование понятия.
Понятие – это логическая мыслительная операция, которая по определённым признакам выделяет предметы из множества и объединяет их в один класс.
Виды понятий
Содержание и объём понятия ложатся в основу разделения понятий на разные виды.
Вся эта довольно сложная типология понятий нужна для того, чтобы мы могли с лёгкостью производить над понятиями операции и определять в каких отношениях друг к другу они находятся.
Отношения между понятиями
Понятия не изолированы друг от друга, наоборот, они находятся во множестве связей с другими понятиями. Умение выявлять эти связи очень важно, так как оно позволяет выявить, когда наш собеседник или автор текста ошибается в употреблении понятий или даже осознанно ими манипулирует. Примерами такой манипуляции могут послужить использование понятий, объёмы которых не равны, как взаимозаменяемых, незаметный переход к понятию с меньшим объёмом для облегчения доказательства своей позиции и т.д.
Логики делят отношения между понятиями на фундаментальные и производные. Фундаментальные отношения первичны, с помощью их различных комбинаций можно задать все остальные отношения. Всего выделяют три фундаментальных отношения: совместимость, включение и исчерпывание.
Понятия совместимы, если пересечение их объёмов непусто. Соответственно, если пересечение их объёмов пусто, то понятия несовместимы.
Понятие А включается в понятие В, если каждый элемент объёма А также является элементом объёма В.
Понятия находятся в отношении исчерпывания, если и только если каждый предмет из универсума рассмотрения является элементом объема либо первого, либо второго понятия.
В результате комбинирования этих фундаментальных отношений можно задать пятнадцать производных отношений между понятиями. Мы расскажем только о тех из них, которые оперируют с непустыми и неуниверсальными понятиями. Их всего шесть.
Равнообъёмность – это отношение, при котором объёмы двух понятий полностью совпадают.
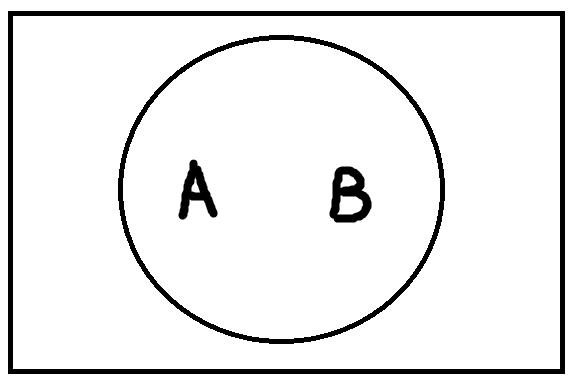
Подчинение возникает тогда, когда объём одного понятия полностью входит в объём другого понятия.
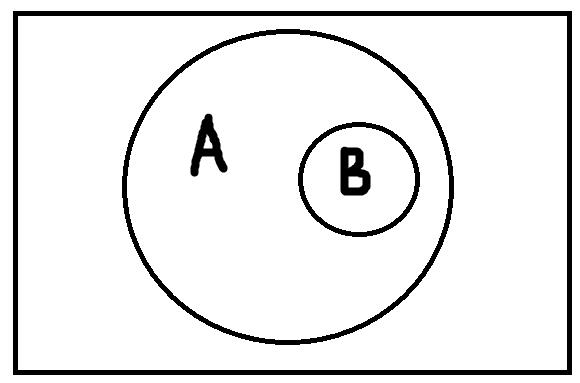
Пересечение – это отношение, при котором объёмы понятий пересекаются, но полностью не совпадают.
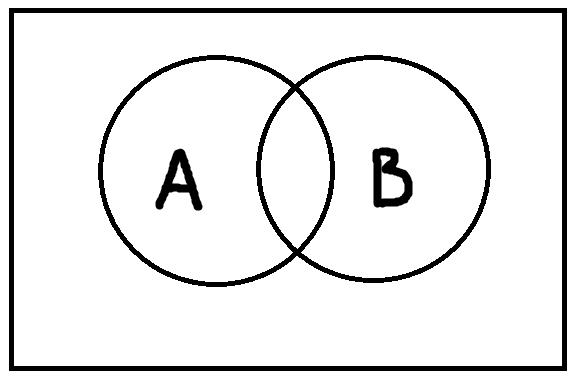
Дополнительность – это такое отношение, когда два понятия пересекаются и при этом исчерпывают собой весь универсум рассмотрения.

Противоречие – это отношение, при котором объёмы понятий не пересекаются и исчерпывают весь универсум.
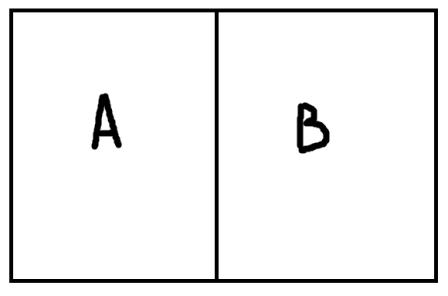
Соподчинение возникает, когда объёмы понятий не пересекаются, но при этом не исчерпывают собой весь универсум рассмотрения.
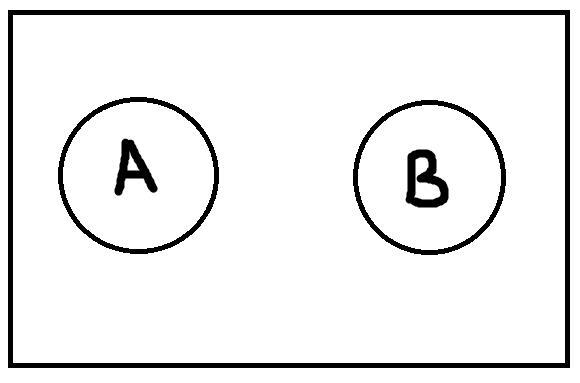
Операции над понятиями
Главная цель операций над понятиями – образование нового понятия, со своим собственным объёмом и содержанием, из имеющихся других или более понятий. Основные операции, совершаемые над понятиями, называются булевыми операциями. Такое наименование они получили в честь английского математика и логика Дж. Буля, который разработал своеобразную логическую математику. Правда, операции, совершаемые над понятиями, похожи на те операции, которые мы научились выполнять с числами в начальной школе. К ним относятся: пересечение, объединение, вычитание, симметрическая разность, дополнение.
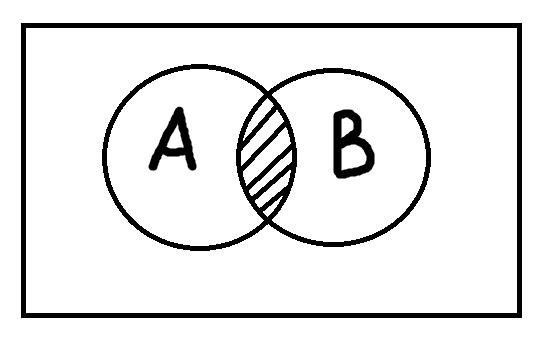
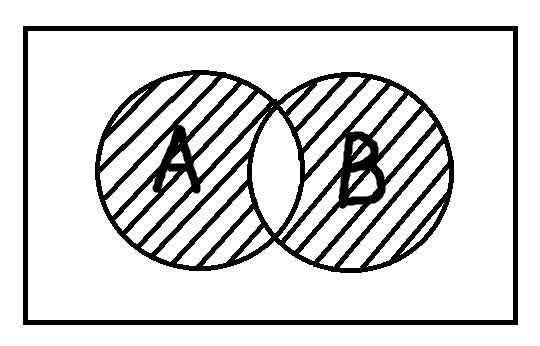
Пересечение понятий – это операция, в ходе которой берутся два или более понятий и как бы накладываются друг на друга. В результате в месте пересечения их объёмов образуется новое понятие, элементами которого будут те предметы, которые одновременно обладают отличительными признаками всех пересечённых понятий. Чтобы представить это наглядно, посмотрим на рисунки:
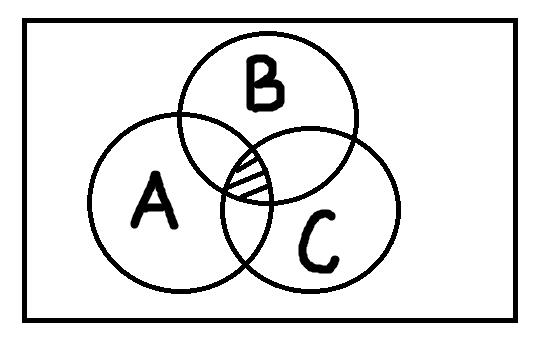
Объединение понятий подобно сложению: мы берём несколько понятий, соединяем их объёмы и тем самым образуем новое понятие, элементами которого будут те предметы, которые обладают хотя бы одним из отличительных признаков объединённых понятий.
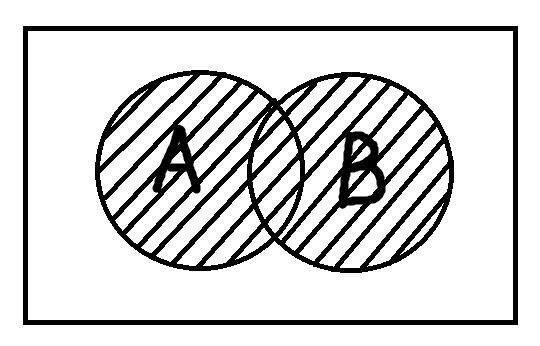
Вычитание понятий опять же очень похоже на математическое вычитание. При вычитании берётся два или более понятий и из объёма одного отнимаются объёмы оставшихся. Таким образом, образуется новое понятие, элементами объёма которого будут предметы, обладающие отличительным признаком первого понятия, но не обладающие отличительными признаками тех понятий, которые из него вычитались.
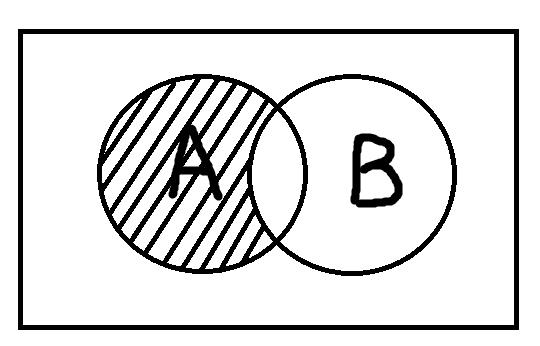
Симметрическая разность – это операция, в некотором смысле обратная пересечению. Нужно точно также взять два или более понятий, наложить их друг на друга, но новое понятие, образованное в результате этого наложения, будет содержать только те элементы, которые обладают не более чем одним отличительным признаком изначальных понятий.
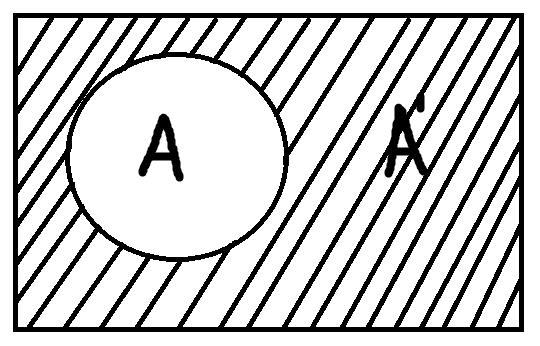
Дополнение – это операция, в ходе которой берётся понятие, а затем его объём как бы вычитается из всего универсума рассмотрения. Так создаётся новое понятие, элементами которого будут только те предметы, которые не обладают отличительным признаком изначально взятого понятия.
Помимо булевых операций над понятиями можно проводить ещё целый ряд операций: ограничение, обобщение, деление.
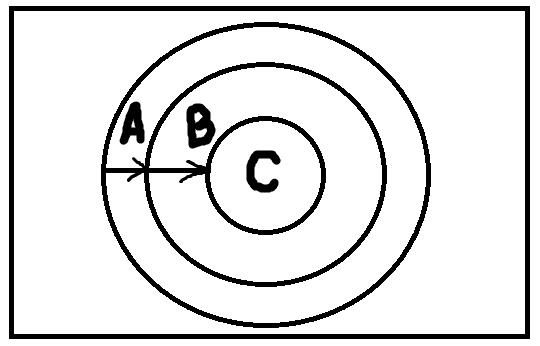
Ограничение – это операция, представляющая собой как бы сужение понятия. Ограничить понятие А означает перейти к понятию В, такому что его объём будет строго включаться в объём понятия А. Причём этот переход от А к В представляет собой переход от родового понятия к видовому.
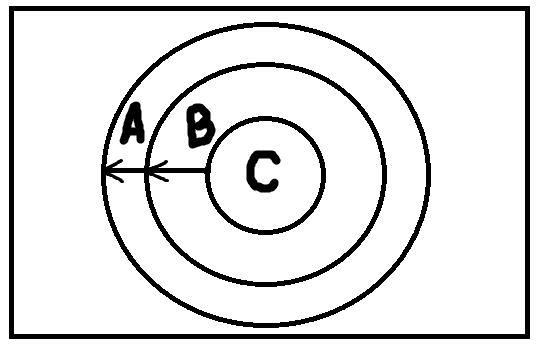
Обобщение – это операция, обратная ограничению. На этот раз мы не сужаем, а расширяем понятие. Обобщить понятие В означает перейти к понятию А, так что объём понятия В будет строго включаться в объём понятия А. Здесь совершается переход от видового понятия к родовому.
Деление – это операция, состоящая в том, что берётся понятие, выделяется какая-то характеристика и на основе варьирования этой характеристики исходное понятие делится на несколько частей, в результате чего получается набор новых понятий. Исходное понятие называют делимым понятием. Те понятия, которые образуются после деления – членами деления. Характеристику, на основе которой осуществляется деление – основанием деления.
Чтобы деление было правильным, необходимо соблюдать следующие условия:
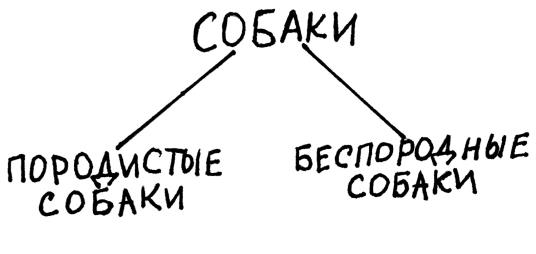
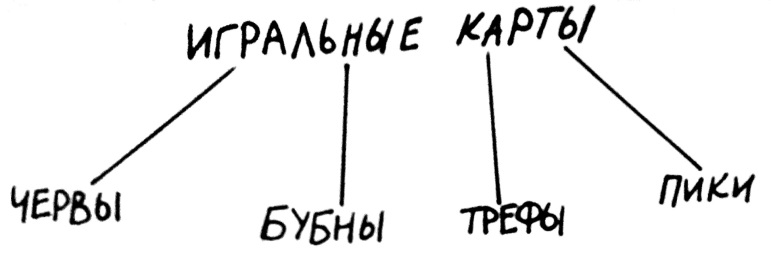
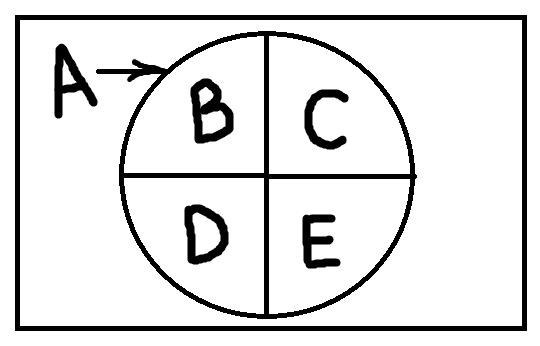
Классификация. Операция деления лежит в основе составления классификаций и типологий. Классификация осуществляется посредством последовательного деления понятия на его виды, видов – на подвиды и т.д. Классификация, прежде всего, важна в научном познании. Она может выступать как результатом изучения какой-то предметной области (всеобщая классификация растений и животных Карла Линнея), так и двигателем исследований (периодическая таблица химических элементов Менделеева). Кроме того, классификации очень важны в обучении: люди гораздо легче воспринимают информацию, если она разложена по полочкам. Часто даже сами того не замечая, мы пользуемся классификациями и в повседневной жизни: ранжирование сотрудников в офисе, организация одежды в шкафу, распределение товаров по отделам в магазине – вот только несколько примеров.
Правильно выполненная классификация подобна перевёрнутому дереву (на мой взгляд, скорее, перевёрнутому кусту). Вершина классификации – исходное делимое понятие – называется корнем. Линии, расходящиеся от неё, подобны веткам. Они ведут к членам деления, от которых в свою очередь также расходятся ветки к новым понятиям. Каждое понятие в классификации называют таксоном. Таксоны группируются по ярусам. На первом ярусе находится корень классификации А. На втором ярусе – таксоны В1-Вn, образованные с помощью первой операции деления. На третьем ярусе – таксоны С1-Сn, образованные в результате второй операции деления и т.д. Каждый ярус может содержать любое количество таксонов.
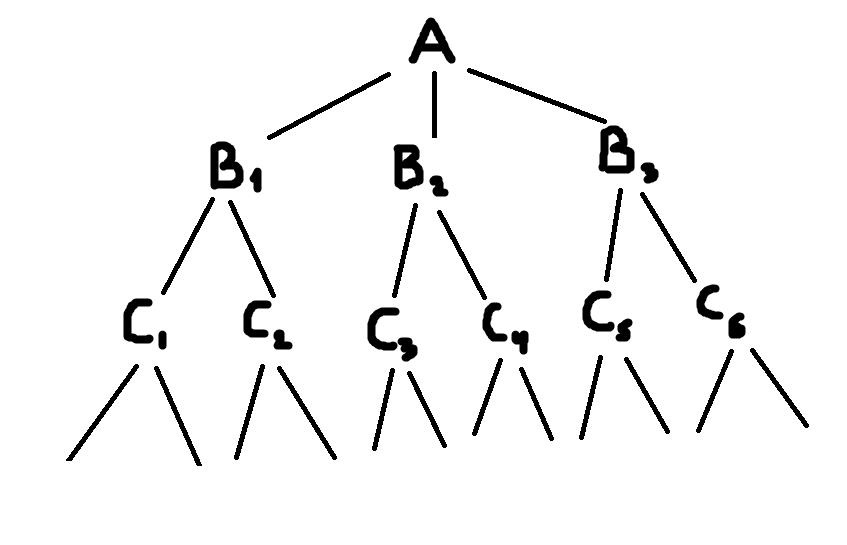
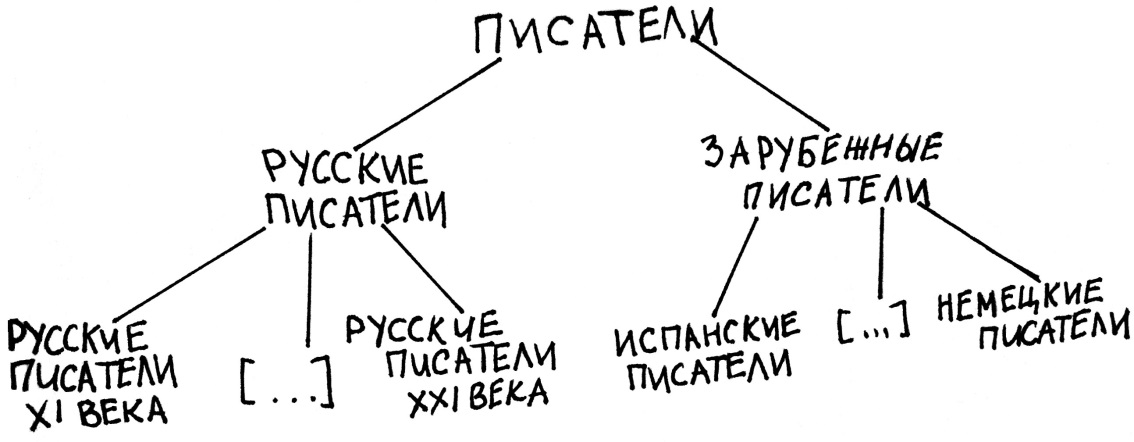
Знаком […] обозначены пропущенные члены деления. Дальше каждый таксон может быть разделён ещё по какому-то своему признаку. Главное в каждом отдельном делении соблюдать перечисленные выше правила.
Упражнения
Попробуйте представить эту классификацию животных в виде дерева. Считаете ли вы, что она выполнена правильно? Если да, то докажите, что ни одно из правил деления в ней не нарушено. Если нет, то объясните, какие именно правила нарушены. Каким образом эту классификацию можно было бы исправить?
Кот. Прости, пожалуйста, за нескромность. Я тебя давно вот о чем хотел спросить…
Кот. Как можешь ты есть колючки?
Кот. В траве попадаются, правда, съедобные стебельки. А колючки… сухие такие!
Осел. Ничего. Люблю острое.
Кот. Не пробовал есть?
Муж: Милая, ты не права.
Жена: Ах, я не права. Значит, я лгу. Я лгу, значит, я плохой человек, то есть нелюдь. Ты хочешь сказать, что я животное? Мама, он меня скотиной назвал!
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.
Читайте также:


