Прочность на изгиб костей

Сельскохозяйственная биология, 2008, № 6, с. 122-125.

МЕТОДИКА ОПРЕДЕЛЕНИЯ ПРОЧНОСТИ КОСТЕЙ ЖИВОТНЫХ С ИСПОЛЬЗОВАНИЕМ ИСПЫТАТЕЛЬНЫХ МАШИН

Н.В. САХНО

Предложена методика определения прочности костей на изгиб с помощью испытательных машин разной конструкции. Использовали имеющиеся установки промышленного производства без их адаптации. Для расчета предела прочности костей на изгиб применили формулу, позволяющую количественно описать равномерное распределение прилагаемой нагрузки к поперечному сечению трубчатых костей. С использованием описанной методики сравнили показатели устойчивости костей на изгиб, сжатие и растяжение у лабораторных животных.

Ключевые слова: остеосинтез, трубчатые кости, биомеханические свойства кости.

В настоящее время имеются данные о том, что прочность костей зависит от вида, возраста, пола, а также условий содержания животного (1, 2). Кроме того, у лактирующих коров выявлены суточные морфометрические изменения костей (3), что также, по нашему мнению, может влиять на их устойчивость к травмированию. Результаты определения прочности костей у животных разных видов вариабельны и до конца не систематизированы. Это, в частности, обусловлено трудоемкостью исследований костной ткани.

Существует методика определения силы внешнего травматического воздействия, для которой расчетная и экспериментальная сила удара различаются незначительно (не более ошибки электротензометрического измерения силы в эксперименте). Однако для проведения исследований по этой методике требуется дорогостоящее и труднодоступное оборудование (4).

Данные о повреждении костных структур представлены в достаточном объеме на примере поперечного сдавливания трубчатых костей и при сжатии плоских костей (5). В то же время нарушение целостности кости возникает чаще при прямом приложении травмирующей силы, провоцирующей сгибательное воздействие на кость (6). При этом приведенные данные о механическом повреждении трубчатых костей под воздействием изгибающей силы в поперечном направлении и под острым углом (5) характеризуют лишь биомеханику компенсаторной перестройки костной ткани, предшествующей возникновению переломов.

Следует также отметить, что при использовании трупного материала для исследования механических свойств кости неизбежно возникают ошибки, поскольку живая кость обладает иными характеристиками и неодинаково реагирует на нагрузки разной интенсивности.

Целью нашей работы была разработка методики определения предельной устойчивости трубчатых костей при нагрузке на изгиб для изучения биомеханических свойств костной ткани и выбора оптимального способа иммобилизации отломков костей в зависимости от характера перелома.

Описание методики. Поскольку в организме независимо от места и угла приложения травмирующей силы вся кость принимает нагрузку, то нами были адаптированы условия испытаний предела прочности костей на изгиб. Расстояние между опорами, на которые укладывали кость перед нагрузкой, составляло 2/3 ее длины. Оставшейся части кости было достаточно для обеспечения относительного покоя в заданном положении до воздействия травмирующей силы, а также исключения соскальзывания с опор при изгибании во время приложения силы. При этом отсутствие фиксации концов кости позволяло принимать прилагаемую нагрузку и перераспределять по всему испытуемому образцу (кости). Условия испытаний были максимально приближены к возникающим при действии травмирующей силы, формирующей переломы по типу сгибания, так как силовое воздействие было плавным с ускорением 20 МПа/с.

Исследуемые кости тщательно препарировали от мышц, сухожилий, связок и жировой ткани. К определению прочности приступали не позже 12-16 ч после эвтаназии. Кости укладывали горизонтально на опоры испытательной установки УИМ-10. Расстояние между опорами изменяли в зависимости от длины образца. Силовое воздействие было направлено сверху непосредственно по центру диафиза кости перпендикулярно к длинной оси, что максимально приближает воздействие к условиям, возникающим при незначительной кинетической энергии травмирующего агента, и дает возможность объективно оценить предельно допустимую нагрузку.

Результаты испытаний фиксировали в момент нарушения целостности кости. Образцы, полученные от собак, испытывали на установке УИМ-10, от кошек (во избежание погрешности измерений) — МИП-1-50035.

Нарушение целостности как интактных костей, так и костей после консолидации отломков происходило в средней трети диафиза. Поэтому условия испытаний позволяли определить прочность регенерата после косых переломов с соответствующей локализацией, что необходимо для оценки сроков и качества перестройки костной ткани при восстановлении биомеханических свойств. На основании определения морфометрических показателей в месте повреждения костей рассчитывали предел прочности на изгиб.

Как известно, максимальное нормальное напряжение при плоском поперечном изгибе определяется отношением максимального изгибающего момента в рассматриваемом сечении к моменту сопротивления сечения относительно оси x (8):

где Fmax — максимальная нагрузка в момент излома кости; L — расстояние между опорами, на которых расположена исследуемая кость; D — наружный диаметр диафиза кости в месте перелома; d — внутренний диаметр диафиза кости в месте перелома.

Предел прочности на изгиб свежих костей животных соответствовал условному напряжению при наибольшей нагрузке, предшествующей их разрушению. Известно, что кость как материал с относительно низкой эластичностью, обладающий небольшим модулем упругости, в момент деформации прогибается незначительно (5).

На 1-е сут после эвтаназии у собак прочность трупной кости, находившейся при комнатной температуре и влажности воздуха практически не изменялась. По истечении 2-3 нед хранения трупной кости в таких же условиях ее прочность может увеличиться (отмечалось повышение упругости на 5 %). В этом случае исследуемая большая берцовая кость по реакции при нагрузке на изгиб приближалась к свежей малой берцовой кости, предел прочности которой можно оценить, лишь значительно сократив расстояние между опорами, что вносит погрешность в определение. В дальнейшем на фоне интенсивной потери влаги кость, освобожденная от мягких тканей, становится хрупкой. Можно заключить, что в живом организме прочность костей максимизируется благодаря содержащейся в них влаге, необходимой для метаболических процессов.

Сравнивая прочность интактных (контроль) и травмированных (опыт) больших берцовых костей собак на 180-е сут после остеосинтеза не установили достоверных различий. При этом нагрузка, вызвавшая перелом костей после остеосинтеза, как правило, была выше контроля, однако рассчитанная прочность — ниже. Для длины кости, расстояния между опорами, диаметра диафиза и костномозгового канала на месте перелома кости, величины нагрузки, вызвавшей перелом, и расчетной прочности показатели (контроль/опыт, M±m) составляли соответственно 179,00±5,10/172,20±5,70; 119,34±3,40/119,46±3,81; 12,20±0,66/14,20±1,16; 5,20±0,49/5,80±0,37 мм; 117,20±18,00/154,00±17,69 кг; 20,49±2,06/17,31±1,89 кг/мм 2 и 200,84±20,17/169,66±18,55 МПа.

Возможная причина выявленного снижения прочности ранее травмированных костей — уменьшение диаметра костномозгового канала за счет эндостальной костной мозоли при увеличении диаметра диафиза вследствие формирования периостальной. То есть компактный слой диафиза в этих костях все еще был толще относительно интактных и выдерживал более высокую нагрузку, что в расчете на 1 мм2 его поверхности (согласно приведенной выше формуле) давало несколько бoльшие значения устойчивости на изгиб.

Следует также отметить высокую устойчивость костей голени (большой и малой берцовой) к нагрузкам. Как указывалось выше, предел прочности малой берцовой кости при нагрузке на изгиб оценить практически невозможно из-за ее высокой деформационной способности. Кости голени представляют собой промежуточное звено в тазовой конечности и испытывают довольно значительные функциональные нагрузки. То есть прочность кости зависит от расположения в скелете и естественных нагрузок.

При анализе прочности длинных трубчатых костей скелета у разных видов животных оказалось, что предел прочности на изгиб отдельных костей периферического скелета кошек превышает исследуемый показатель у собак в 1,3-1,7 раза. Для длины кости, расстояния между опорами, диаметра диафиза и костномозгового канала на месте перелома кости, величины нагрузки, вызвавшей перелом, и расчетной прочности показатели (интактная большая берцовая кость/интактная плечевая кость, M±m) составляли соответственно 113,00±1,64/94,17±1,01 мм (Р ≤0,05); 75,32±0,89/62,80±0,68 мм (Р ≤ 0,05); 7,30±0,42/7,20±0,48; 3,20±0,10/3,60±0,07 мм (Р ≤ 0,05); 66,00±1,52/58,80±0,89 кг (Р ≤ 0,05) и 36,59±6,81/27,12±4,92 кг/мм 2 .

Отметим, что у кошек компактный слой диафиза большой берцовой кости был в среднем в 2,03 раза тоньше, чем у собак, а диаметр диафиза значительно снижал объем кости, противодействующий нагрузке.

Более высокая устойчивость костей у кошек, вероятно, связана с большей нагрузкой в процессе эволюции (несмотря на относительно небольшую массу большинства представителей кошачьих): прыжками, падениями с высоты, способностью животных приземляться на конечности независимо от положения тела в момент падения и т.д.

Таким образом, методика адаптации условий испытаний предела прочности костей на изгиб на установках, используемых при контроле качества промышленных изделий, позволяет оценить биомеханические свойства кости у разных видов животных. Оказалось, что предел прочности костей у интактных и ранее травмированных собак (после остеосинтеза) достоверно не различался. Это позволяет сделать заключение о стабильности использованного способа иммобилизации отломков при косых переломах, обеспечивающего формирование к 6 мес после остеосинтеза регенерата, равноценного по прочности интактной кости.

Л И Т Е Р А Т У Р А

METHOD OF DETERMINATION OF BONE STRENGTH IN ANIMALS WITH USE OF TESTING MACHINE

N.V. Sakhno

The technique for determination of bone strength on the bend with the help of industrial test-ing machines (without adaptation) of different construction was proposed. For the calculation of bone bending strength the author uses the formula which permits to describe the uniform distribution of a load to cross-section of tubular bones. With the application of this method the parameters of bones strength on the bend, the pressure and the stretching in laboratorial animals have been compared.

Key words: osteosynthesis, the tubular bones, biomechanical qualities of the bone.

Поступила в редакцию 17 апреля 2007 года

Для характеристики прочностных свойств костей используют четыре вида механического воздействия на кость: сжатие, изгиб, растягивание и кручение.

Прочность костей на сжатие:т.е. в направлении обычной при их жизни нагрузки - достаточно велика: в продольном (нагрузка идет сверху вниз) направлении несущая способность костей следующая:

1. Бедренной кости более 4500 кг.- у мужчин и 3900 кг.- у женщин;

2. Большеберцовой кости более 3500 кг.- у мужчин и 2800 кг.- у женщин;

3. Плечевой кости более 2500 кг.- у мужчин и 2100 кг.- у женщин;

4. Лучевой кости 900 кг. - у мужчин и около 800 кг у женщин;

Прочность костей на изгиб:в переднезаднем направлении, т.е. в направлении перпендикулярно вертикально стоящей кости значительно меньше:

1. Бедренная кость выдерживает изгиб под нагрузкой 250 кг.

2. Большеберцовая кость выдерживает изгиб под нагрузкой 260 кг.

3. Плечевая кость выдерживает изгиб под нагрузкой 130 кг.

4. Лучевая кость выдерживает изгиб под нагрузкой 50 кг.

5. Более мелкие кости обладают и меньшей прочностью (Jamada, 1970).

Прочность костей на растяжение:при растягивающей продольной силе кость выдерживает напряжение 15 300 кг/см 2 . Подобная характеристика делает нашу кость прочнее дуба и почти равна чугуна.

Прочность костей на скручивание: при обычной ходьбе момент скручивающих сил могут достигать 1 530 кг/см 2 . Это величина несколько раз меньше предела прочности костей: для разрушения большеберцовой кости момент скручивающей силы должен достигать 14 280 кг/см 2 . Это цифры считаются сниженными т.к. были получены на трупном материале.

Подвижное соединение костей (суставы)

Сустав – элемент ОДА, обеспечивающий соединение костных звеньев и создающий подвижность костей друг относительно друга. Суставы являются наиболее совершенными видами соединения костей. У человека их около 200.

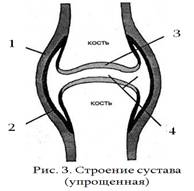
Сустав образуют суставные поверхности сочлененных костных звеньев. Между суставными поверхностями имеется суставная полость, в которую поступает синовиальная жидкость. Окружает сустав суставная капсула, состоящая из плотной соединительной ткани.

Основной функцией суставов является обеспечение подвижности костных звеньев друг относительно друга. С этой целью поверхность суставов смачивается синовиальной жидкостью (смазкой), которая выделяется суставным хрящом при увеличении нагрузки на сустав. При уменьшении нагрузки синовиальная жидкость поглощается суставным хрящом. Чтобы компенсировать разрушение суставного хряща при трении в нем постоянно происходят процессы регенерации. С позиции медико-биологических наук в спорте кости скелета человека чаще всего выступают в виде стержней, соединенных одни или несколькими суставами образующих при этом кинематические цепи. В теле человека почти 200 суставов. Более 100 костей могут перемешаться относительно друг друга благодаря наличию суставов. Различают непрерывное и прерывное соединение костей.

Суставами соединяются кости, которые выполняют функцию движения. В каждом суставе различают (см. рис. 3):

v суставная сумка (1)

v синовиальная оболочка (2)

v суставный хрящ (3)

v полость с синовиальной жидкостью (4).

5. Суставы классифицируют по следующим принципам:

По числу суставных поверхностей различают:

Простой сустав - имеющий только две суставные поверхности, например межфаланговые суставы.

Сложный сустав - имеющий более двух сочленовных поверхностей, например локтевой сустав. Сложный сустав состоит из нескольких простых сочленений, в которых движения могут совершаться отдельно.

Комплексный сустав - содержащий внутрисуставной хрящ, который разделяет сустав на две камеры (двухкамерный сустав). Деление на камеры происходит или полностью, если внутрисуставной хрящ имеет форму диска (например, в височно-нижнечелюстном суставе), или неполностью, если хрящ приобретает форму полулунного мениска (например, в коленном суставе).

Комбинированный сустав представляет комбинацию нескольких изолированных друг от друга суставов, расположенных отдельно друг от друга, но функционирующих вместе. Таковы, например, оба височно-нижнечелюстных сустава, проксимальный и дистальный лучелоктевые суставы и др.

5.1 По форме и функции суставных поверхностей различают:

Трехосные суставы - осуществляется движение вокруг трех осей. Одна из суставных поверхностей образует выпуклую, шаровидной формы головку, другая вогнутую суставную впадину. Различают:

1. Шаровидные (Плечевой сустав)

2. Чашеобразные (Тазобедренный сустав)

Двухосные суставы - осуществляется движение вокруг двух осей. Сочленовные поверхности представляют отрезки эллипса: одна из них выпуклая, овальной формы с неодинаковой кривизной в двух направлениях, другая соответственно вогнутая. Они обеспечивают движения вокруг 2 горизонтальных осей, перпендикулярных друг другу: вокруг фронтальной - сгибание и разгибание и вокруг сагиттальной - отведение и приведение. Связки в эллипсовидных суставах располагаются перпендикулярно осям вращения, на их концах. Различают:

1. Седловидные (запястнопястный сустав)

2. Эллипсоидные (затылочная кость и I шейным позвонком)

Одноосные суставы-цилиндрическая суставная поверхность, ось которой располагается вертикально, параллельно длинной оси сочленяющихся костей или вертикальной оси тела, обеспечивает движение вокруг одной вертикальной оси. Различают:

1. Плоские (суставы между суставными отростками позвонков);

2. Цилиндрические (сочленение между локтевой и лучевой костями);

3. Блоковидные (межфаланговые суставы)

Для тренера, кроме знаний в анатомии важно знать и углы движений суставов, характеризующие границы подвижности суставов. Необходимо подчеркнуть, что подвижность в суставах зависит от следующих факторов:

1. от краев суставных поверхностей;

2. от растяжимости связок;

3. от связности со стороны мышц.

Трения в суставах

В суставах чрезвычайно низок коэффициент трения, составляющий приблизительно 0,01. По современным научным представлениям, низкие коэффициенты трения в суставах объясняются трем причинами:

Первая причина: микроскопические исследования показывают, что внешне гладкая поверхность гиалинового хряща напоминает губку с очень тонкими порами, пропитанную синовиальной жидкостью, которую можно из неё выжать. В месте контакта губчатых хрящей большую площадь занимает не сам хрящ, а жидкость, заключенная в порах. Пока жидкость не выдавилась из пор, трение контактируемых поверхностей невелико. Выдавливание происходит значительно медленнее, чем всасывание после освобождения поверхностей. Это обусловлено тем, что жидкость на участке контакта частей одного сустава движется преимущественно вдоль соприкасающихся поверхностей, тогда как в освободившиеся поверхности она входит в перпендикулярном к ним направлении.

Вторая причина: состоит в особенностях самой синовиальной жидкости. Синовия отличается от плазмы крови в основном тем, что в ней имеется "присадка" - гиалуроновая кислота (полисахарид с длинными цепями). Этот разбавленный раствор обладает некоторыми упругими свойствами.

Третья причинам: при сжатии его между гладкими поверхностями он выдавливается в стороны лишь до некоторого минимального расстояния. Дальше поверхности перестают сближаться, а при освобождении даже слегка отходят друг от друга. При сжатии синовии между хрящевыми губками молекулы гиалуроновой кислоты проходят в поры много хуже, чем растворяющаяся плазма. Концентрация полимеров в месте контакта возрастает и это ещё в большей степени способствует удержанию поверхностей от непосредственного контакта.

Четвертая причина: выявлено, что с увеличением скорости движения в суставе вязкость синовии снижается, и трение в суставе уменьшается. Это явление обусловлено дроблением содержащихся в синовии полимерных молекул. При уменьшении скорости цепочки молекул полисахарида вновь восстанавливаются

Расчеты показали, что при ходьбе работа против сил трения в тазобедренном суставе эквивалентна работе по подъему тела человека на высоту равную 0,32 мм. Эта значит, что величина энергии на преодоление трения в соединениях опорного аппарата сравнительно невелика даже при значительных нагрузках.

Дата добавления: 2018-08-07 ; просмотров: 744 ;

Аннотация научной статьи по математике, автор научной работы — Ткач Г. Ф.

Данная статья посвящена проблеме математического и компьютерного моделирования прочностных характеристик костей скелета животных разного возраста с учетом медицинских аспектов и использованием достижений в смежных областях технической науки, в том числе известных решений классических задач и их применимости в конкретных условиях. Компьютерное моделирование модели кости при помощи программного обеспечение PRO/Engineer позволяет наглядно продемонстрировать сложную зависимость распределения нагрузки в кости, при которой возникают предельные напряжения (разрыв). Представленная математическая модель оценки механической прочности кости крыс разного возраста подтверждена экспериментальными исследованиями.

TECHNIQUE OF MATHEMATICAL AND COMPUTER MODELING TO DEFINE MECHANICAL FLEXURAL STRENGTH OF HUMERAL BONE IN ANIMALS OF DIFFERENT AGE

The article is devoted to the mathematical and computer calculating and modeling of strength-related characteristics of skeletal bones in animals of different age taking into account the medical aspects and the achievements in mechanical science. Computer modeling of bones by means of the PRO/Engineer software allows to create visually difficult dependence of loading distribution in a bone subjected to ultimate strength. This mathematical model helps estimate mechanical strength of bones in rats of different age that is confirmed by experiments.

УДК 004.925.8:539.413:616.717.5/6-053-092.9 Ткач Г.Ф.

МЕТОДИКА МАТЕМАТИЧЕСКОГО И КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ ОПРЕДЕЛЕНИЯ МЕХАНИЧЕСКОЙ ПРОЧНОСТИ НА ИЗГИБ ПЛЕЧЕВОЙ КОСТИ ЖИВОТНЫХ РАЗНОГО ВОЗРАСТА

Медицинский институт Сумского государственного университета, Украина

Данная статья посвящена проблеме математического и компьютерного моделирования прочностных характеристик костей скелета животных разного возраста с учетом медицинских аспектов и использованием достижений в смежных областях технической науки, в том числе известных решений классических задач и их применимости в конкретных условиях. Компьютерное моделирование модели кости при помощи программного обеспечение РКО/Епдтеег позволяет наглядно продемонстрировать сложную зависимость распределения нагрузки в кости, при которой возникают предельные напряжения (разрыв). Представленная математическая модель оценки механической прочности кости крыс разного возраста подтверждена экспериментальными исследованиями.

Ключевые слова: математическое моделирование,

Кость является физиологически динамической системой не только в период роста и восстановления, но и в течении всей жизни. У взрослого человека кость содержит 30% органических и 70% неорганических веществ[1]. Именно от этих соединений зависит ее твердость и гибкость. Сочетание же твердости и эластичности называют прочностью кости [11].

В современной науке для удобства изучения явлений часто используют компьютерные модели, которые реально повторяют все их свойства. Математическое моделирование находит всё большее и большее применение в различных областях медицины, в частности морфологии [4,10].

Механические испытания образцов композитных материалов, к которым относятся кости, вызывают затруднения, поскольку им присущи такие свойства как хрупкость и вязкость одновременно [3,12]. В лабораторных условиях можно провести эксперименты, дающие связь между приложенной силой и возникшими изменениями в образце до разрушения [8,9]. Сложная геометрия кости, неоднородность и анизотропия ее упругих свойств приводят к тому, что даже простое давление на кость, например, сжатие вдоль

кости скелета, физические нагрузки, крысы, продольной оси, приводит к сложным ее деформациям [3,7].

Вот почему проблема прочностных характеристик костей скелета является сложной и многогранной. Ее можно рассматривать с позиций медицины, материаловедения, механики и пр. Во многих областях науки эта задача уже ставилась и в определенной мере исследована [5,13]. Морфологические особенности формирования повреждений длинных трубчатых костей при сложных напряженно-деформированных состояниях (с позиций биомеханики) изучены недостаточно, а математическое моделирование процессов разрушения в современной медицине носит эпизодический характер[6].

Цель работы - построение математической модели плечевой кости крыс разного возраста и определение с помощью математических расчетов процесса ее разрушения в условиях статической нагрузки.

Материал и методы

Исследования проведены на плечевых костях 60-ти белых крыс-самцов неполовозрелого (3 и 4-х мес.), репродуктивного (6 и 8 мес.) и старческого (20 и 22 мес.) возрастов. Содержание животных и эксперименты проводились согласно положениям "Европейской конвенции о защите позвоночных животных, которые используются для экспериментов и других научных целей" (Страсбург, 1985). Животных выводили из эксперимента путем передозировки парами эфира и проводили скелетирование их плечевых костей.

Для проведения опытов использовали установку, показанную на рисунке 1

Исследуемую кость 1 располагали на двух призмах 3 так, как схематично показано на рис.

2. Для измерения прогиба использовали микрометр 2, который жестко закреплен на не-деформируемом элементе.

Рис. 1. Опытная установка.

поперечном сечении кости при изгибе.

Силу, под действием которой будет изгибаться кость, прилагали строго посередине между опорами. Нагрузку на кость постепенно увеличивали с помощью грузов, накладывая их на нагрузочное приспособление. Полученные данные обрабатывались статистически на персональном компьютере с использованием пакета прикладных программ. Достоверность расхождения экспериментальных и контрольных данных оценивали с использованием критерия Стьюдента, достоверной считали вероятность ошибки меньше 5% (р Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Физически это означает, что поперечное сечение можно представить как тонкую, абсолютно жесткую пластинку, получающую в результате деформации испытываемого образца линейное смещение и углы поворота. Перемещение точки А поперечного сечения вдоль оси 7. по гипотезе плоских сечений будет следующим:

(Рх Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

где Е - модуль упругости материала, ат - коэффициент теплового линейного расширения, АТ - изменение температуры материала. Для оси 7 из уравнения (в) следует, что

сг = Е ■ £ - Е ■ ат ■ АТ , ч 1 , (г)

а с учетом равенства (б) получим

Величина 0 представляет собой деформацию элемента, совпадающего с осью испытываемого образца (геометрическим местом центров тяжести сечения).

йсрх Л Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

йсрх _ Мх \рЕ-у-ат-М■

жесткость при растя-

жесткость при изгибе

Так как кость имеет постоянный модуль упругости, то

Г=[ Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Так как действует только одна сила, то будет действовать в этой же плоскости только один

момент. Учитывая что У , У и

то, что реакции опор и моменты действуют в одной плоскости, получим окончательную формулу для определения предела прочности при из-

Максимальный изгибающий момент находим

по формуле: 4 как показано на эпю-

На основании закона Гука из формулы

^ найдем радиус кривизны продольной оси в момент разрушения кости, как показано на рис. 4:

Е - модуль упругости.

- прогиб при изгибе, измеренный с помощью микрометра (рис. 2)

Полученные формулы позволяют теоретически обосновать проекцию и координату приложения силы, а также возникновение и формирование морфологической картины разрушения длинных трубчатых костей, сечение которых

может быть круглой, треугольной, квадратной формы и в каждом конкретном случае имеет свою специфику при механическом воздействии. Этот процесс сложный и многогранный.

Результаты и их обсуждение: Для наглядности распределения напряжений при изгибе был использован модуль программного обеспечение РКО/Епдтеег, где кроме наглядного процесса распределения нагрузки определяем место разрыва и нагрузку, при которой возникают предельные напряжения (разрыв) [4].

Рис. 5 Эпюры изгибающего момента М и поперечной силы Р.

Frxne 5 of 8 Sire^i v..n Mses ¡WCSi !kg / inn sec""2> i De'orirecl

Рис. 6. Распределение напряжений в кости при ее испытании на изгиб, с помощью программного

Результат программного моделирования дал определенную перспективу для дифференциальной диагностики скорости распределение напряжений в кости при ее испытании на изгиб, а также конфигураций истинного разрушения и в компьютерной модели.

Представленные результаты исследования и их краткое теоретическое обоснование не пре-

Расчетные данные костей

тендуют на полноту изложения механизмов локального разрушения длинных костей скелета, как многослойного биокомпозитного материала. В настоящей работе предпринята попытка построения математической модели разрушения костей скелета в месте приложения силы, которая подтверждена экспериментальными исследованиями представленными в таблице 1.

; разного возраста при их испытаниях на изгиб.

Рассчитываемые параметры ед.изм. неполовозрелые половозрелые старые

95 дней 115 дней 180 дней 200 дней 600 дней 660 дней

Приложенная нагрузка в момент разрыва Р н 81,4±0,13 89,2±0,24 99,4±0,31 103,0±0,28 92,3±0,46 81,4±0,21

Прогиб У мм 0,07±0,002 0,08±0,001 0,08±0,002 0,07±0,001 0,05±0,002 0,04±0,001

Момент сопр. попер, сечения W мм куб. 13,00±0,04 14,63±0,05 17,28±0,07 18,15±0,07 19,30±0,09 19,12±0,04

Изгибающий момент М Н*мм 407,00±25,7 460,80±31,3 542,37±37,4 570,56±25,4 524,69±37,3 461,04±36,7

Предел прочности на изгиб о МПа(Н/м м кв.) 31,31 ±0,25 31,50±0,19 31,39±0,18 31,44±0,23 27,19±0,44 24,11±0,32

Радиус кривизны г мм 39,73±0,47 42,97±0,52 47,81 ±0,28 47,84±0,33 53,46±0,28 59,51±0,62

Таким образом, представленная математическая модель, подтвержденная экспериментальными исследованиями, с учетом индивидуальной пространственной геометрии плечевой кости и предложенная методика компьютерного построения расчетной модели весьма специфичны и могут быть использованы в качестве определения биомеханических и прочностных характеристик костей скелета.

Математическое моделирование сложно-напряженного деформированного состояния длинной трубчатой кости является перспективным методом исследования, позволяющим определять механические закономерности и адаптационные изменения в костной ткани при снижении и увеличении механической нагрузки на кость в различных условиях.

Перспективы дальнейших разработок в данном направлении. Математическое моделирование конструкций костей скелета и определение прочностных характеристик при изгибе, растяжении, сжатии и кручении в норме и в условиях нарушений водно - солевого обмена организма в возрастном аспекте.

1. Аврунин A.C. Уровни организации минерального матрикса костной ткани и механизмы, определяющие параметры их форми-

рования/ А.С. Аврунин, P.M. Тихилов, А.Б. [и др.] // Морфология. - 2005. - Т. 127, №2. - С. 78-82.

Баженов В.А. Численные методы в механике / Баженов В.А., Дащенко А.Ф., Оробей В.Ф., Сурьянинов Н.Г. - Одесса : «СТАНДАРТЫ), 2005. — 563 с.

Дж. Герман. Механика разрушения кости / Дж. Герман, Г. Либо-виц. - М. : Мир, 1976. Т.7, 4.2. - 469 с.

Зинковский А.Б. Биомеханическое компьютерное моделирование опорно-двигательного аппарата человека: основные задачи и приложения / А.Б. Зинковский, А.А Иванов, В.А. Шолуха // Науч. ведомости СПбГТУ. - 1998 - № 2-3 - С.143-148. Костенко Н.А. Сопротивление материалов / Н.А. Костенко, С.В. Балясникова, Ю.Э. Болошановская. - М.: Изд-во Высшая школа, 2004,- 430с.

Леонова Е. Н. Морфология разрушения диафизов длинных трубчатых костей под воздействием острого индентора при различных условиях опирания: автореф. дис. на соискание ученой степени канд. мед. наук: спец. 14.00.24 - "Судебная медицина" / Е. Н. Леонова - М. 2009. -20с

Образцов И.Ф. Проблемы прочности в биомеханике: Учебное пособие / И.Ф Образцов, И С Абрамович, А.С. Барер. - М. : Изд-во В. Школа, 1988. - 311 с.

Персов.Б.3. Расчет и проектирование экспериментальных установок / Персов.Б.3. - СПбГУ: НИЦ, 2006. - 348 с. ("Регулярная и хаотическая динамика", Институт компьютерных исследований)

Саргсян А.Е. Сопротивление материалов, теории пластичности и упругости: учебник / Саргсян А.Е. - [2-е изд.]. - М. : Высшая школа, 2000. -. 290 с.

Чирков О.Ю. Подходы к математическому моделированию разрушения биокомпозита, являющегося условным аналогом костей свода черепа / О.Ю. Чирков, В.А. Клевно, В.Б. Маркин // Альманах судебной медицины. - 2001. - №2. - С.38-43. Hart R.T. Theories of bone modeling and remodeling, in Bone Mechanics / R.T. Hart, D.T. Davy. - S.C.Cowin, Ed., CRC Press, Boca Raton, FL, 1989. - chap. 11.-P. 253-277.

Stephen C. Cowin. Bone mechanics handbook / C.Stephen Cowin. - Florida: Corporate Blvd., Boca Raton, 2001,- 1934 p. Yuehuei H. An. Mechanical testing of bone and the bone - implant interface/ H. An.Yuehuei, A. Robert Draughn. - Florida Corporate Blvd., Boca Raton, 2001. - 625 p.

МЕТОДИКА МАТЕМАТИЧНОГО I КОМПЬЮТЕРНОГО МОДЕЛЮВАННЯ ВИЗНАЧЕННЯ МЕХАН1ЧН01 ТРИВКОСТ1 НА ЗГИН ПЛЕЧОВО! К1СТКИ ТВАРИН Р13НОГО В1КУ ТКАЧ Г.Ф.

Ключов1 слова: математичне моделювання, кютки скелета, ф1зичы навантаження, щури.

Резюме: Стаття присвячена проблем! математичного й комп'ютерного моделювання тривкюних характеристик кюток скелета тварин р1зного в1ку з урахуванням медичних аспекте \ використанням дося-гнень у сум1жних областях техычноТ науки, у тому числ1 вщомих р1шень класичних задач та Тх застосу-вання в конкретних умовах. Комп'ютерне моделювання модел1 кюток за допомогою програмного за-безпечення РКО/Епдтеег дозволяе наочно вщтворити складну залежнють розподту навантаження в кютц1, при якш виникають граничш напруги (розрив). Розроблена математична модель оцшки мехашч-но'Г мщносп кютки щур1в р1зного в1ку, яка пщтверджена експериментальними дослщженнями.

TECHNIQUE OF MATHEMATICAL AND COMPUTER MODELING TO DEFINE MECHANICAL FLEXURAL STRENGTH OF HUMERAL BONE IN ANIMALS OF DIFFERENT AGE Tkach G.F.

Keywords: mathematical model, skeletal bones, physical loads, rats.

УДК: [612.821.3/.5: 612.82]:37.011.32(055)

Ткаченко Е.В., Алиреза Шадфард, Мортеза Фазели Ниаки, Хамед Сартипи Носратолла, Соболь А.

ИЗУЧЕНИЕ ПРОЦЕССОВ ТЕРМИН00БРА30ВАНИЯ И ОЦЕНКА УРОВНЯ ИНТЕЛЛЕКТА У ИРАНСКИХ СТУДЕНТОВ В ЗАВИСИМОСТИ ОТ ИХ ПРОФИЛЯ МЕЖП0ЛУШАРН0Й АСИММЕТРИИ

В статье приведены результаты изучения коэффициента интеллекта и процессов терминооб-разования у Иранских студентов УМСА. Нами получены следующие результаты. Истинные левши и амбидекстры обладали более высоким коэффициентом интеллекта, чем скрытые и ложные левши и правши. Определение терминов оказалось легче всего для амбидекстров; сравнение и различение терминов - для правшей; обнаружение логических связей - для правшей и амбидекстров. В построении свободных классификаций лидировали истинные и скрытые левши, а также амбидекстры. Полученные результаты могут быть объяснены с точки зрения различий в выполнении когнитивных операций правым и левым полушарием головного мозга с учётом по-лушарного доминирования у выделенных субпопуляциях студентов.

Ключевые слова: интеллект, правши, левши, амбидекстры, межполушарная асимметрия.

Известно, что в психологии и физиологии су- тестами и зависит от биологического интеллекта ществует несколько подходов к анализу приро- и социокультурных факторов (воспитания, обу-

1) Биологический интеллект - генетически детерминированная биологическая база когнитивного функционирования и всех его индивидуальных различий. Биологический интеллект, возникая на основе нейрофизиологических и биохимических факторов, непосредственно связан с деятельностью коры больших полушарий.

2) Психометрический интеллект - измеряется

чения, местных культуральных особенностей региона временного или постоянного проживания индивида).

3) Социальный или практический - интеллектуальные способности, проявляющиеся в повседневной жизни [7]. Он зависит от психометрического интеллекта, личностных особенностей, обучения, социоэкономического статуса.

Иногда биологический интеллект обозначают как интеллект А, социальный как интеллект Б. Очевидно, что интеллект Б гораздо шире, чем А, и включает его в себя.

Ещё в середине прошлого века с появлением первых экспериментальных приёмов измерения простых психофизиологических показателей (различительная сенсорная чувствительность, время реакции и т.д.) в психологии возникло направление, ставящее своей целью найти простые физиологические процессы или свойства, которые могут лежать в основе индивидуальных различий по интеллекту. Идея использования простых, имеющих физиологическую природу показателей для оценки индивидуальных различий по интеллекту идёт от Френсиса Гальто-на. Он рассматривал интеллект как биологическое образование, которое нужно измерять с помощью физиологических индикаторов. Рекомендовалось в качестве коррелята интеллекта и

Читайте также: