У кого есть шпоры по технической механике
Уравновешенные силы:
Система сил, под действием которой свободное твердое тело может находится в покое, называется уравновешенной.
Аксиомы статики:
а) Аксиома о уравновешенных силах (о абсолютном твердом теле) - две одинаковые силы, приложенные к абс. твердому телу и действуют вдоль одной прямой в противоположных направлениях назыв. уравновешенными силами. б) Аксиома о прибавлении или вычитании уравновешенной системы сил - действие системы сил на твердое тело не меняется, если если прибавить к ней уравновешенные силы. в) Аксиома сложения сил - силы, которые действуют на точку, можно складывать как векторы или аналитично. г) Аксиома о опорах (связи) и их реакции - силы могут быть активными и пассивными. Первые стремятся вызвать ускорение матер. точек. Другие - ограничивают движение. Они возникают как реакции системы на движение или на действие активных сил. Движение матер. точек может быть свободным или ограниченным. Во втором случае тело или точка назыв. несвободной. Все, что ограничивает движение тел в пространстве называется опорой (связью). д) Аксиома о освобождении от связи (опоры) - механическое состояние системы материальных точек не изменится, если освободить ее от связей, меняя их силами, действие которых такое же, как и связей (опор). Эти силы назыв. реакциями связей - пассивные силы, которые направлены в противоположную сторону относительно ограничения движения.
Момент силы относительно точки.
Вращательный эффект силы характеризуется ее эффектом. Моментом силы относительно центра О называется величина, равная взятому с соотв. знаком произведению модуля силы на длину плеча.
Момент силы относительно оси.
Моментом силы относительно оси называется скалярная величина, равная моменту проэкции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью.
Пара сил, момент пары. Свойства пар сил.
Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абс. твердое тело. Моментом пары наз. величина, равная взятому с соотв. знаком произведению модуля одной из сил пары на ее плечо (Понятие момента силы связано с точкой, относительно к-рой берется момент. Момент пары определяется только ее моментом и плечом; ни с какой точкой плоскости эта величина не связана). Св-ва : сумма моментов сил пары относительно точки не зависит от выбора точки и всегда равняется моменту пары, Пара сил не имеет равнодействующей - нельзя уравновесить одной силой.
Сложение пар сил.
Система пар, лежащих в одной плоскости, эквивалентна одной паре, лежащей в той же плоскости и имеющей момент, равный алгебраической сумме моментов слагаемых пар.
Теорема Вариньона.
О моменте равнодействующей - момент равнодействующей плоской системы сходящихся сил относительно любого центра равен алгебраической сумме моментов слагаемых сил относительно того же центра.
Виды нагрузок.
а) Сосредоточенная, б) Рассредоточенная равномерная и неравномерная, в) Пара сил - момент.
Параллельный перенос сил. Приведение системы сил к одному центру.
Силу можно переносить в любую точку тела, к-рая называется точкой приведения, если прибавить при этом пару сил (в точку приведения).
Главный вектор и главный момент произвольной системы сил.
Все силы, которые действуют на тело можно привести к одной точке, при этом вместо сил имеем эквивалентную систему сил, которая состоит из главного вектора и главного момента (пара сил). Частные случаи приведения произвольной системы сил к одному центру - а) главный момент равен равнодействующей, если главный момент М=0, б) Fгол=0, Мгол<>0, в) Fгол<>0, Мгол<>0, Мгол перпендик. Fгол - плоская система сил. г) Мгол<>0 Fгол<>0 Мгол || Fгол - силовой винт. е) Fгол=0, Мгол=0 - равновесие тела.
Условия равновесия произвольной пространственной системы сил.
S - сумма, Мгол = S Мi(F) = 0; Fгол = S Fi = 0;
Написать проекции на все оси.
Условия равновесия произвольной плоской системы сил.
а)Одной проекции силы нет, зато есть один момент с индексом этой оси б) есть два момента - нет двух сил в) Все моменты равны нулю.
Формы условий равновесия. .
Центр параллельных сил - это точка приложения равнодействующей системы параллельных сил.
Центр тяжести однородного тела.
Центр тяжести плоской фигуры.
Трение скольжения, угол трения.
Закон Кулона-Амонтона - F=fN. Угол трения - это угол, тангенс к-рого равен коэффициенту трения - предельный угол силы к нормали пов-ти, чтобы тело поехало.
Кинематика:
Теоремы о скоростях.
а) Проекции скоростей (абсол. твердого тела) двух точек на прямую, которая проходит через них равны. б) Скорость любой точки складывается из скорости какой-либо другой точки, принятой за полюс, и скорости ее вращения вокруг этой точки.
Мгновенный центр скоростей. Связь скоростей точек с мгновенными радиусами при п.п.д.
МЦС - это точка в плоскости движения, скорость к-рой в данный момент времени равна нулю.
Способы определения мгновенного центра скоростей.
Динамика точки и системы:
Основное уравнение динамики для свободной и несвободной материальной точки в векторной, координатной и естественной формах.
Теорема – о независимом действии сил – если на точку действует несколько сил или равнодействующая то точка будет двигаться с ускорением = сумме ускорений, к-рые возникают при действии каждой силы отдельно.
Вывести и сформулировать принцип Даламбера для точки.
ma = F + N; F + N + (-ma) = 0; Ф = -ma; - сила инерции.
Решение второй задачи динамики точки.
Это - зная силы найти закон движения. а) Показываем начальное и конечное положение тела. б) Направляем ось х из начального в конечное положение, ось у – перпендикулярно х с начального положения, в) Показываем тело в свободном положении и действующие на него силы, г) составляем дифур движения точки в проекции на ось х, д) интегрируем это уравнение, е) находим постоянные интегрирования с начальных условий и неизвестные величины. That all.
Две основные меры механического движения точки.
Импульс (кол-во движения) и кинетическая энергия.
Работа силы, когда тело вращается.
Теорема об изменении кинетической энергии точки.
Изменение кинетической энергии точки при некотором ее перемещении равно сумме работ внешних сил, которые действуют на этом перемещении на точку.
Идеальные связи – сумма возможных работ реакций которых равна нулю.
Возможные перемещения, возможная работа силы.
Возможное перемещение – это бесконечно малые перемещения точек мех. системы, которые мы представляем и которые разрешены связями. Возможные работы находятся по таким же правилам как и действительные, но вместо дифференциалов записываются их вариации.
Принцип Лагранжа-Даламбера (Общее уравнение динамики)
Связи, классификация связей.
а) геометрические (без производных), б) кинематические (дифференциальные rj’=V), в) интегрируемые (это кинемат. К-рые можно привести к геометрич. rj=s), г) односторонние, д) двухсторонние, е) нестационарные –f(t).
Принцип возможных перемещений.
Необходимыми и достаточными условиями для равновесия мех. системы, к которой приложены двусторонние, стационарные и идеальные связи, есть равенство нулю суммы возможных работ всех активных сил на любых возможных перемещениях из положения равновесия.
Обобщенные координаты, скорости, силы.
Обобщенная сила – это коэффициент при вариации обобщенной координаты в выражении возможной работы.





Описание книги "Техническая механика. Шпаргалка"
Описание и краткое содержание "Техническая механика. Шпаргалка" читать бесплатно онлайн.
Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.
Техническая механика. Шпаргалка
1. Аксиомы и понятие силы статики
Теоретическая механика – это наука о механическом движении твердых материальных тел и их взаимодействии. Механическое движение понимается как перемещение тел в пространстве и во времени по отношению к другим телам, в частности, к Земле.
Статика изучает условия равновесия тел под действием сил.
Кинематика рассматривает движение тел как перемещение в пространстве; характеристики тел и причины, вызывающие движение, не рассматриваются.
Динамика изучает движение тел под действием сил.
Сила – это мера механического взаимодействия материальных тел между собой. Взаимодействие характеризуется величиной и направлением, т. е. сила – это величина векторная, характеризующаяся точкой приложения, направлением (линией действия), величиной (модулем).
Силы, действующие на тело (или систему сил), делят на внешние и внутренние. Внешние силы бывают активные и реактивные. Активные силы вызывают перемещение тела, реактивные стремятся противодействовать перемещению тела под действием внешних сил.
Системой сил называют совокупность сил, действующих на тело.
Эквивалентная система сил – система сил, действующая так же, как заданная.
Уравновешенной (эквивалентной нулю) системой сил называется такая система, которая, будучи приложенной к телу, не изменяет его состояния.
Систему сил, действующих на тело, можно заменить одной равнодействующей, действующей так, как система сил.
Все теоремы и уравнения статики выводятся из нескольких исходных положений, называемых аксиомами.
Первая аксиома. Под действием уравновешивающей системы сил абсолютно твердое тело или материальная точка находятся в равновесии или движутся равномерно и прямолинейно (закон инерции).
Вторая аксиома. Две силы, равные по модулю и направленные по одной прямой в разные стороны, уравновешиваются.
Третья аксиома. Не нарушая механического состояния тела, можно добавить или убрать уравновешивающую систему сил (принцип отбрасывания системы сил, эквивалентной нулю).
Четвертая аксиома (правило параллелограмма сил). Равнодействующая двух сил, приложенных к одной точке, приложена к той же точке и является диагональю параллелограмма, построенного на этих силах как на сторонах.
Пятая аксиома. При взаимодействии тел всякому действию соответствует равное и противоположно направленное противодействие.
Следствие из второй и третьей аксиом. Силу, действующую на твердое тело, можно перемещать вдоль линии ее действия.
2. Связи и реакции связей
Все тела делятся на свободные и связанные.
Свободные тела – это тела, перемещение которых не ограничено.
Связанные тела – это тела, перемещение которых ограничено другими телами.
Тела, ограничивающие перемещение других тел, называют связями.
Силы, действующие от связей и препятствующие перемещению, называют реакциями связей. Реакция связи всегда направлена с той стороны, куда нельзя перемещаться.
Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей).
Связи делятся на несколько типов.
Связь – гладкая опора (без трения) – реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре.
Гибкая связь (нить, веревка, трос, цепь) – груз подвешен на двух нитях. Реакция нити направлена вдоль нити от тела, при этом нить может быть только растянута.
Жесткий стержень – стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня. Стержень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи.
Возможным перемещением точки называется такое бесконечно малое мысленное перемещение, которое допускается в данный момент.
Шарнирная опора. Шарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров.
Подвижный шарнир. Стержень, закрепленный на шарнире, может поворачиваться вокруг шарнира, а точка крепления может перемещаться вдоль направляющей (площадки). Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, так как не допускается только перемещение поперек опорной поверхности.
Неподвижный шарнир. Точка крепления перемещаться не может.
Стержень может свободно поворачиваться вокруг оси шарнира. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Ее изображают в виде двух составляющих: горизонтальной и вертикальной (Rx, Ry).
Под действием внешних сил в опоре возникают реактивная сила и реактивный момент Мz, препятствующий повороту.
Реактивная сила представляется в виде двух составляющих вдоль осей координат:
3. Определение равнодействующей геометрическим способом
Система сил, линии действия которых пересекаются в одной точке, называется сходящейся.
Необходимо определить равнодействующую системы сходящихся сил (F1; F2; F3;…; Fn), где n – число сил, входящих в систему.
В соответствии со следствиями из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными к одной точке.
Используя свойство векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил.
При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.
Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называется геометрическим.
Многоугольник сил строится в следующем порядке.
1. Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпал с началом последующего.
2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.
3. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.
Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.
Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.
Если в системе три силы, образуется треугольник сил.
Геометрическим способом пользуются, если в системе три силы. При решении задач на равновесие тело считается абсолютно твердым (отвердевшим).
Задачи решаются в следующем порядке.
1. Определить возможное направление реакций связей.
2. Вычертить многоугольник сил системы, начиная с известных сил, в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура).
3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.
4. Для уточнения определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.
4. Определение равнодействующей аналитическим способом
Проекция сил на ось определяется отрезком оси, отсекаемой перпендикулярами, опущенными на ось из начала и конца вектора.
Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением сил. Проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси.
Проекция силы на две взаимно перпендикулярные оси.
Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определим равнодействующую аналитическим способом. Выберем систему координат, определим проекции всех заданных векторов на эти оси. Складываем проекции всех векторов на оси х и у.

Техническая механика. Шпаргалка
1. Аксиомы и понятие силы статики
Теоретическая механика – это наука о механическом движении твердых материальных тел и их взаимодействии. Механическое движение понимается как перемещение тел в пространстве и во времени по отношению к другим телам, в частности, к Земле.
Статика изучает условия равновесия тел под действием сил.
Кинематика рассматривает движение тел как перемещение в пространстве; характеристики тел и причины, вызывающие движение, не рассматриваются.
Динамика изучает движение тел под действием сил.
Сила – это мера механического взаимодействия материальных тел между собой. Взаимодействие характеризуется величиной и направлением, т. е. сила – это величина векторная, характеризующаяся точкой приложения, направлением (линией действия), величиной (модулем).
Силы, действующие на тело (или систему сил), делят на внешние и внутренние. Внешние силы бывают активные и реактивные. Активные силы вызывают перемещение тела, реактивные стремятся противодействовать перемещению тела под действием внешних сил.
Системой сил называют совокупность сил, действующих на тело.
Эквивалентная система сил – система сил, действующая так же, как заданная.
Уравновешенной (эквивалентной нулю) системой сил называется такая система, которая, будучи приложенной к телу, не изменяет его состояния.
Систему сил, действующих на тело, можно заменить одной равнодействующей, действующей так, как система сил.
Все теоремы и уравнения статики выводятся из нескольких исходных положений, называемых аксиомами.
Первая аксиома. Под действием уравновешивающей системы сил абсолютно твердое тело или материальная точка находятся в равновесии или движутся равномерно и прямолинейно (закон инерции).
Вторая аксиома. Две силы, равные по модулю и направленные по одной прямой в разные стороны, уравновешиваются.
Третья аксиома. Не нарушая механического состояния тела, можно добавить или убрать уравновешивающую систему сил (принцип отбрасывания системы сил, эквивалентной нулю).
Четвертая аксиома (правило параллелограмма сил). Равнодействующая двух сил, приложенных к одной точке, приложена к той же точке и является диагональю параллелограмма, построенного на этих силах как на сторонах.
Пятая аксиома. При взаимодействии тел всякому действию соответствует равное и противоположно направленное противодействие.
Следствие из второй и третьей аксиом. Силу, действующую на твердое тело, можно перемещать вдоль линии ее действия.
2. Связи и реакции связей
Все тела делятся на свободные и связанные.
Свободные тела – это тела, перемещение которых не ограничено.
Связанные тела – это тела, перемещение которых ограничено другими телами.
Тела, ограничивающие перемещение других тел, называют связями.
Силы, действующие от связей и препятствующие перемещению, называют реакциями связей. Реакция связи всегда направлена с той стороны, куда нельзя перемещаться.
Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей).
Связи делятся на несколько типов.
Связь – гладкая опора (без трения) – реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре.
Гибкая связь (нить, веревка, трос, цепь) – груз подвешен на двух нитях. Реакция нити направлена вдоль нити от тела, при этом нить может быть только растянута.
Жесткий стержень – стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня. Стержень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи.
Возможным перемещением точки называется такое бесконечно малое мысленное перемещение, которое допускается в данный момент.
Шарнирная опора. Шарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров.
Подвижный шарнир. Стержень, закрепленный на шарнире, может поворачиваться вокруг шарнира, а точка крепления может перемещаться вдоль направляющей (площадки). Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, так как не допускается только перемещение поперек опорной поверхности.
Неподвижный шарнир. Точка крепления перемещаться не может.
Стержень может свободно поворачиваться вокруг оси шарнира. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Ее изображают в виде двух составляющих: горизонтальной и вертикальной (Rx, Ry).
Под действием внешних сил в опоре возникают реактивная сила и реактивный момент Мz, препятствующий повороту.
Реактивная сила представляется в виде двух составляющих вдоль осей координат:
3. Определение равнодействующей геометрическим способом
Система сил, линии действия которых пересекаются в одной точке, называется сходящейся.
Необходимо определить равнодействующую системы сходящихся сил (F1; F2; F3;…; Fn), где n – число сил, входящих в систему.
В соответствии со следствиями из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными к одной точке.
Используя свойство векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил.
При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.
Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называется геометрическим.
Многоугольник сил строится в следующем порядке.
1. Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпал с началом последующего.
2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.
3. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.
Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.
Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.
Если в системе три силы, образуется треугольник сил.
Геометрическим способом пользуются, если в системе три силы. При решении задач на равновесие тело считается абсолютно твердым (отвердевшим).
Задачи решаются в следующем порядке.
1. Определить возможное направление реакций связей.
2. Вычертить многоугольник сил системы, начиная с известных сил, в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура).
3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.
4. Для уточнения определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА шпаргалка
. . . . . . . .29. Составное движение точки
30. Основные понятия динамики.
1. Основные понятия
Основные законы механики
Свободное падение тела
2. Сходящиеся силы на плоскости
без учета сопротивления воздуха.
3. Равнодействующая сходящихся
Движение тела, брошенного
сил на плоскости. Леммы
под углом к горизонту без учета
4. Теория пар сил, лежащих в одной
Движение падающего тела
плоскости. Момент силы
с учетом сопротивления воздуха . . . . . .
относительно точки на плоскости . . . .
Колебательное движение точки.
5. Система сил, произвольно
. . . . . . .расположенных на плоскости
6. Условия равновесия сил,
материальной точки, апериодическое
приложенных к рычагу.
движение точки. Явление биений.
Сцепление и трение скольжения
7. Система сходящихся сил
в пространстве. Уравнение
и его малые колебания . . . . . . . . . . . . . . .
. .8. Теория пары сил в пространстве
. . . . . . . .движения материальной точки
9. Главные моменты системы сил . . . .
Система материальных точек . . . . . .
Твердое тело. Моменты инерции
системы сил к главному вектору
. . . . . . . . . . . . . .и к главному моменту
. . .39. Центробежные моменты инерции
40. Теорема о движении центра масс
пространственных систем сил.
Сложение параллельных сил
в пространстве. Центр тяжести тела .
движения механической системы . . . . .
Импульс силы и его проекции
для определения положения
Центр тяжести некоторых
линий, плоских фигур и тел
Моменты количества движения
Основные понятия кинематики . . .
материальной точки относительно
. . . . . . . . . . .центра и относительно оси
Работа. Теоремы о работе силы . . . .
Классификация движений точки
Работа сил тяжести,
по ускорениям ее движения
Движение. Путь. Скорость
и касательное ускорение точки . . . . .
об изменении кинетической
. . . . . . . . . .энергии материальной точки
Силовое поле. Потенциальное
силовое поле и силовая функция.
.и центростремительного ускорений
Плоское движение твердого тела
Мгновенный центр скоростей
и вращательного движения
и подвижной центроиды . . . . . . . . . . . .
Теорема об ускорениях точек
плоской фигуры и ее следствия.
и его малые колебания
Динамика плоского движения
Определение ускорений точек
Понятие о гироскопе . . . . . . . . . . . . .
и угловых ускорений звеньев
Потеря кинетической энергии
при ударе двух тел
Общее уравнение динамики.
Ускорения точек твердого тела
Принцип возможных перемещений
при сферическом движении . . . . . . . .
в случае движения системы.
Теорема о скоростях точек
свободного твердого тела и ее
общего уравнения динамики
следствия. Теорема об ускорениях
точек свободного твердого тела . . . . .

1. Основные понятия
и аксиомы статики
Статика — это раздел теоретической механики, в коF тором устанавливаются методы преобразования одF них систем сил в другие, им эквивалентные, а также условия равновесия различных систем сил, действуюF щих на твердое тело.
Материальная точка — это простейшая модель маF териального тела любой формы, размеры которого достаточно малы и которое можно принять за геометF рическую точку, имеющую определенную массу.
Механическая система — это любая совокупность материальных точек.
Абсолютно твердое тело — это механическая система, расстояние между точками которой не измеF няется при любых взаимодействиях.
Сила — это одна из векторных мер действия одного материального объекта на другой рассматриваемый объект. Сила характеризуется числовым значением, а также точкой приложения и направлением действия. Это в е кторная величина и обозначается она, наприF
Система сил — это совокупность сил, действующих на рассматриваемое тело.
Система сил, эквивалентная нулю (равновесная система сил), — это такая система сил, действие коF торой на твердое тело или точку, находящиеся в покое или движущиеся по инерции, не приводит к изменеF нию его состояния.
Существуют следующие аксиомы.
1. О равновесии системы двух сил. Для равновеF сия системы 2Fх сил, приложенных к точкам твердого тела, необходимо и достаточно, чтобы эти силы были
3а 3. Равнодействующая сходящихся сил на плоскости.
Леммы о нулевых стержнях
Равнодействующая сила при равновесии системы R =0 представляет собой замыкающую силового мноF гоугольника, или векторную сумму сил, однако, с друF гой стороны,
Следовательно, условия равновесия системы схоF дящихся сил в аналитической форме будут
Иными словами, для равновесия системы сходяF щихся сил, действующих на твердое тело, необходиF мо и достаточно, чтобы суммы проекции этих сил на каждую из двух прямоугольных координат осей, лежаF щих в плоскости, были равны нулю.
Фермы — это конструкции, которые состоят из прямолинейных стержней, соединенных между собой шарнирами и образующих неизменяемую геометриF ческую фигуру.
Существует определенная зависимость между коF личеством стержней ( n ) и количеством шарниров ( k ). В основном треугольнике имеются 3 стержня и 3 узла. При этом для образования одного узла требуются
2а 2. Сходящиеся силы на плоскости
Система сходящихся сил — это такая система сил, линии действия которых пересекаются в одной точке — центре пучка. П у сть задана произвольная система сходящихся сил F 1 , F 2 , . F n , приложенных к твердому телу. Сложение двух сходящихся сил
графически осуществляется по правилу параллелоF грамма,
П о правилу параллелограмма складываем силы R 12 и F 3 , и получаем их равнодействующую
R 123 = R 12 + F 3 = F 1 + F 2 + F 3 ;
Для плоской системы сходящихся сил одну из коордиF натных осей (обычно OZ ) выбирают перпендикулярF ной силам. Таким образом, каждая из сил пучка даст проекцию на эту ось, равную нулю, а значит, будет равна нулю и проекция равнодействующей силы на ось OZ . После этого проецируют векторы векторF ного равенства на прямоугольные оси координат. ТогF да в соответствии с теоремой о проекции замыкающей получится
R x = ∑ F ix , R y = ∑ F iy .
4а 4. Теория пар сил, лежащих в одной плоскости. Момент силы
относительно точки на плоскости
Система двух равных по модулю параллельных сил, направленных в противоположные стороны, называется п а рой сил . Пара сил, как правило, прилагается к телу ( F 1 , F 2 ), которое должно вращаться. Плоскость, в коF торой расположены пары сил, называется плоскос$ тью действия пары сил N . Кратчайшее расстояние между линиями действия сил пары называется пле$ чом пары h . Алгебраический момент пары сил —
это взятое со знаком плюс или минус произведение одной из сил пары на плечо пары сил:
M = M ( F 1 , F 2 ) =± Fd .
Алгебраический момент пары сил имеет знак плюс, если пара сил стремится вращать тело против часовой стрелки, и знак минус, если пара сил стремится враF щать тело по часовой стрелке. Алгебраический моF мент пары сил не зависит от переноса сил пары вдоль своих линий действия и может быть равен нулю, если линии действия пары сил совпадают. Произведение модуля силы на плечо силы относительно этой точки
называют алгебраическим моментом пары отно$
сительно точки. Плечо пары h относительно точ$ ки — это кратчайшее расстояние между этой точкой и линией действия силы. Две пары сил называются
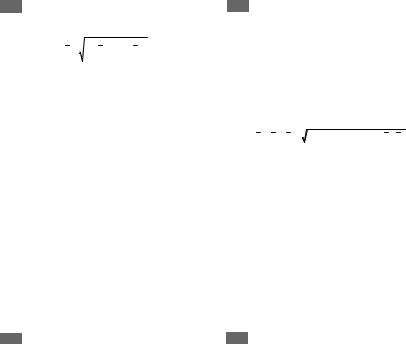
2б По проекциям определяют модуль равнодейстF вующей силы и косинусы углов ее с осями коорF
динат по формулам
R = ( ∑ F ix ) 2 +( ∑ F iy ) 2
cos ( R x , x ) = R x / R , cos ( R y , y ) = R y / R .
Следовательно, си с тема n сходящихся сил эквиваF лентна одной силе R , которая и является равнодейF ствующей этой системы сил. Процесс последовательF ного применения правила параллелограмма означает по сути построение многоугольника из заданных сил . Этот силовой многоугольник называют замкнутым .
Геометрическое условие равновесия системы сходящихся сил. Для равновесия системы сходяF щихся сил необходимо и достаточно, чтобы равнодейF ствующая сила равнялась нулю R = 0.
Теорема о трех силах. Если твердое тело под дейF ствием трех сил, две из которых пересекаются в одной точке, находится в равновесии, то линии действия таF ких трех сил пересекаются в одной точке. Для случая трех сходящихся сил при равновесии силовой треF угольник, построенный из трех сил, должен быть замкF нутым.
4б эквивалентными , если их действие на твердое тело одинаково при прочих равных условиях, а также если они имеют одинаковые по модулю и наF
правлению векторные моменты.
Теорема об эквивалентности пары сил. Пару сил, действующую на твердое тело, можно заменить друF гой парой сил, расположенной в той же плоскости действия и имеющей одинаковый с первой парой алF гебраический момент.
Пару сил как жесткую фигуру можно поворачивать
и переносить в плоскости ее действия как угодно. У пары сил можно изменять плечо и силы, сохраняя при этом алгебраический момент пары и плоскость действия. Эти операции над парами сил не изменяют их действия на твердое тело.
Теорема о сумме алгебраических моментов пары сил. Пары сил, действующие на твердое тело
и расположенные в одной плоскости, можно привести к одной паре сил, алгебраический момент которой раF вен сумме алгебраических моментов составляющих пар сил:
Пары сил, расположенные в параллельных плосF костях, также складываются, поскольку их предвариF тельно можно перенести в одну плоскость. Если сложеF ние выполнять графически, когда векторные моменты пары сил находятся в одной плоскости, то векторный момент эквивалентной пары сил будет иметь вид заF мыкающей векторного многоугольника, построенного из векторных моментов заданных пар сил.
1б равны по модулю и действовали вдоль одной прямой, проходящей через точки их приложеF
ния, в противоположных направлениях.
2. О добавлении системы сил, эквивалентной ну$ лю. Если на твердое тело действует система сил, то
к ней можно добавить систему сил, эквивалентную нулю.
3. Аксиома параллелограмма сил. Две силы, дейF ствующие в одной точке твердого тела или на одну маF териальную точку, можно заменить одной равнодейF ствующей силой, равной по модулю и направлению диагонали параллелограмма, построенного на заданF ных силах:
R = F + F = F 2 + F 2 + 2 F 2 F 2 cos F , F .
1 2 1 2 1 2 1 2
4. Аксиома о равенстве сил действия и противо$ действия. Всякой силе действия есть равная протиF воположная сила противодействия.
Несвободное твердое тело — это тело, не имеюF щее возможность совершать в рассматриваемый моF мент любые перемещения в пространстве.
Аксиома связи: всякую связь можно отбросить или заменить силой, реакцией связей или систе$ мой сил . Реакция связи — это сила, с которой связь действует на систему материальных точек или тверF дое тело. Сила реакции связи направлена в сторону, противоположную направлению перемещения рассматF риваемого тела.
3б 2 стержня. Значит, для образования ( k – 3) узлов нужно 2( k – 3). Общее число стержней:
Нулевыми называются стержни, ненагруженные силой, на концах которых находятся точечные шарниF ры и весом которых можно пренебречь.
Способ вырезания узлов заключается в том, что каждый узел вырезается из фермы и рассматриваетF ся отдельно, как находящийся в равновесии. Система сил, действующих на стержень, — это плоская систеF ма сходящихся сил, которая находится в равновесии. Построение силовых многоугольников всегда начиF нают с узла, в котором сходятся 2 стержня. Каждый последующий узел следует выбирать так, чтобы в нем сходилось не более двух стержней с неизвестными усилиями. Если усилия разрезанных стержней направF лены по стержням в сторону узла, то их называют сжи$ мающими , а если наоборот — растягивающими .
Леммы о нулевых стержнях.
1. Если в узле, не нагруженном внешними силами, сходятся три стержня, и которых два направлены вдоль одной прямой, то усилие в третьем стержне равно нулю, т. е. он является нулевым.
2. Стержень находится в равновесии под действием двух сил, приложенных в шарнирах, где силы равны по величине и противоположны по направлению, т. е. его реакция также будет направлена по оси стержня.

5а 5. Система сил, произвольно расположенных на плоскости
Приведение силы к заданному центру. Силу можно переносить параллельно самой себе в любую точку твердого тела, добавляя при этом пару сил, векF торный момент которой равен векторному моменту переносимой силы относительно новой точки прилоF жения силы.
Теорема Пуансо. Любую произвольную систему сил, действующих на твердое тело, можно в общем случае привести к силе и паре сил.
Главный вектор системы сил — это вектор, котоF рый равен векторной сумме этих сил. Главный вектор системы сил изображается вектором, замыкающим силовой многоугольник, построенный на силах:
Главный момент системы сил относительно точ$ ки тела — это сумма векторных моментов всех сил системы относительно этой точки. Главный момент L 0 равняется сумме векторных моментов присоединеF ния пар:
Уравнения равновесия системы сил, произ$ вольно расположенных на плоскости. Пусть кажF дая из сил расположена в одной плоскости с осями координат ОX , ОY , и потому ее моменты относительF
7а 7. Система сходящихся сил в пространстве. Уравнение
Система сходящихся сил — это такая система сил, линии действия которых пересекаются в одной точке — центре пучка. Для аналитического опредеF ления равнодействующей силы выбирают систему прямоугольных осей координат. Проецируя векторы векторного равенства на прямоугольные оси коордиF нат, получают
Читайте также:


