Все формулы по статистике с описанием шпора

Статистическая группировка

Формула Стерджесса (для определения оптимального числа групп):

где n — число групп;

N - число единиц совокупности.

Величина равного интервала:

где x_max, x_min — наибольшее и наименьшее значения признака,

Относительные показатели

Относительные показатели динамики называются темпами роста. (ОПД)

ОПД =	Текущий показатель
Предшествующий или базисный показатель

Относительный показатель плана (ОПП)

ОПП =	Показатель, планируемый на (i +1) период
Показатель, достигнутый в i-м периоде

Относительный показатель реализации плана (ОПРП)

ОПРП =	Факт текущего периода
План текущего периода

Относительный показатель структуры (ОПС)

ОПС =	Показатель, характеризующий часть совокупности
Показатель всей совокупности в целом

Относительные показатели координации (ОПК)

ОПК =	Показатель, характеризующий i-ю часть совокупности
Показатель, характеризующий часть совокупности, выбранную в качестве базы сравнения

Относительный показатель интенсивности (ОПИ)

ОПИ=	Показатель, характеризующий явление А
Показатель, характеризующий среду распространения явления А

Относительный показатель сравнения (ОПСр)

ОПСр =	Показатель, характеризующий объект А
Показатель, характеризующий объект Б

Темпы прироста рассчитываются по следующим формулам:

Цепной

Базисный

Средние величины

Средняя арифметическая:

-простая (невзвешенная)

-взвешенная

Средняя гармоническая:

-средняя гармоническая простая

-средняя гармоническая взвешенная

Средняя геометрическая.

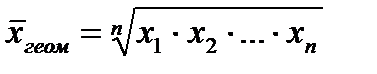
Средняя хронологическая.

Х=(
х₁ + х₂ +х₃+…+х _n_-1+
х _n) : (n-1)

Средняя квадратическая.

Мода

хм₀ — нижняя граница модального интервала;

h — величина модального интервала;

f_Мо — частота модального интервала;

f_Мо-1 — частота интервала, предшествующего модальному;

f_Мо+1 — частота интервала, следующего за модальным.

Медиана

x₀ — нижняя граница интервала, в котором находится медиана;

- сумма частот или число членов ряда;

f_M_е_-1 —накопленная частота в интервале, предшествующем медианному;

f_Me — частота в медианном интервале;

h — величина интервала;

k — число групп.

Абсолютные показатели вариации

Размах вариации

Среднее линейное отклонение

По формуле средней арифметической простой

По средней арифметической взвешенной

;

Дисперсия

Дисперсия обозначается греческой буквой
(сигма) в квадрате и равна

При равенстве весов или когда они равны 1,

Среднее квадратическое отклонение:

равно корню квадратному из суммы квадратов отклонений индивидуальных значений признака от их средней, т.е. из дисперсии:

Тема 1: Группировка статистических данных

Определение числа групп (если группи-ка по непрер. приз-ку или дискрет. со многими знач-ями)

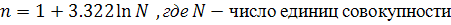
Определение величины равного интервала:

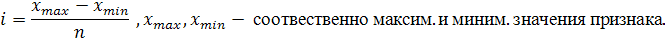
Тема 2: Абсолютные и относительные величины

Относительные величины:

1) относит. вел-на структуры:

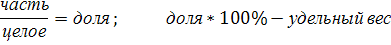
2) относит. вел-на планового задания:

3) относит. вел-на выполнения плана:

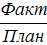
4) относит. вел-на динамики или темп роста:

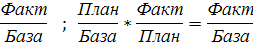
5) относит. вел-на сравнения

6) относит. вел-на интенсивности (пример: фондоотдача = объем/стоимость (один год))

Тема 3: Средние величины и показатели вариации

Средняя арифметическая

простая: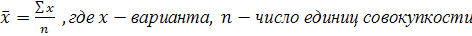

взвешенная: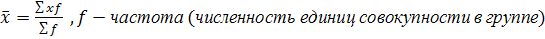

Средняя гармоническая

простая: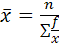

взвешенная: 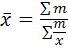, сумма значений признака по группе

Свойства средн. арифметической:

если каждую вари-ту х умен-ть или увел-ть на одно и то же число, то ср. вел-на умен-ется или увел-ется на это же число;

если каждую вари-ту х умен-ть или увел-ть в одно и то же число раз, то ср. вел-на умен-ется или увел-ется в одно и то же число раз;

если каждую частоту f умен-ть или увел-ть в одно и то же число раз, то ср. вел-на не изменится.

Ср. вел-на зависит от вар-ты х и структуры совок-сти, кот. харак-ется долями d.

Ряд распределения имеет 3 центра:

1) ср. аримет-кое;

2) мода – наиболее часто встречающаяся вар-та [M₀];

3) медиана – вар-та, стоящая в середине ряда распре-ния. Сначала находят N медианы, кот. равен n/2, если число еди-ц совок-сти n – чётное, или 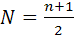, если число еди-ц совок-сти нечетное [M_e].

Осн. пока-ли вариации:

1) размах вариации:

2) ср. линейное отклонение (ср. арифм-кая из абсолют. откл-ний отдел. значений)

Для несгруппир. данных: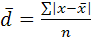

Для сгруппир. данных: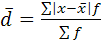

3) ср. квадратическое отклонение (хар-ет ср. абсол. откл-ние вар-ты от ср. вел-ны)

Для несгруппир. данных: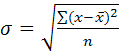

Для сгруппир. данных:

4) Дисперсия – квадрат среднеквадр-ного откл-ния

Для несгруппир. данных: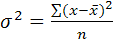

Для сгруппир. данных: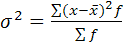

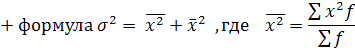
Общая дисперсия: (для сгрупп.) (для несгрупп.)

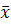
– ср. вел-на резул. приз-ка в сово-сти, 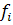- частота (в совокупности!)

Внутригрупповая дисперсия: 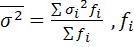- кол-во вариант в группе i

Междугрупповая дисперсия: 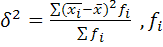- кол-во вариант в группе i

Правило сложения дисперсий: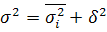

Не имеет еди-ц измерения.

5) Коэффициент вариации хар-ет ср. относит. откл-ние вар-ты от ср. вел-ны.

Способ моментов

Часто мы сталкиваемся с расчетом средней арифметической упрощенным способом.

В этом случае используются свойства средней величины. Метод упрощенного расчета называется способом моментов, либо способом отсчета от условного нуля.

Способ моментов предполагает следующие действия:

1) Выбирается начало отсчета (из х) – условный нуль (A). Обычно как можно ближе к середине распре-ния.

2) Находятся отклонения вариантов от условного нуля ().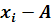

4) Если эти отклонения содержат общий множитель (k), то рассчитанные

отклонения делятся на этот множитель.

Способ моментов:

Средняя: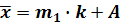

Дисперсия: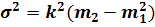

Тема 4: Выборочное наблюдение

Обозначения в теории выборки:

N – числи-ль генер. выборки

n – числи-ль генер. выборки

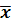
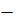
генер. средняя (оценивают)

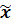
– выбор. средняя (рассчитывают)

p – генер. доля (оценивают)

w – выбор. доля (рассчитывают)

P(t) – задаваемый уровень веро-сти

Генер. средняя: 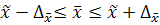с задан. уровнем вероя-сти P(t)

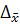
– ошибка выборки для ср. вел-ны

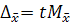
, t – критерий надеж-сти, его вел-на зав-т от уровня задан. вероя-сти P(t)

Если 1) P(t) = 0,683, то t=1; 2) P(t) = 0,954, то t=2 ; 3) P(t) = 0,997, то t=3

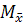
– среднеквадр. ошибка выборки

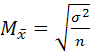
– верна для повторного отбора в выборке.

- для бесповторного отбора

Доказано: 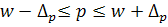с задан. уровнем вероя-сти P(t)

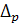
– ошибка выборки для доли

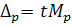
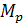
, – среднеквадр. ошибка выборки для доли

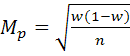
–для повторного отбора

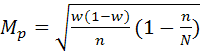
- для бесповторного отбора

Выборочное наблюдение – наблюдение с помощью специальных методов отбора
Обследование основного массива – наблюдение за частью наиболее крупных единиц в исследуемой совокупности
Монографическое наблюдение или обследование – подробное описание отдельных единиц наблюдения в статистической совокупности (изучение новых методов управления, инновационных подходов и т.п.)

Способы опроса – Саморегистрация, Экспедиционный опрос, Корреспондентский опрос
Мониторинг — специальное организованное систематическое наблюдение за состоянием явлений и процессов, объектов совокупности (процесс непрерывного слежения)
Процесс статис наблюдения — определяется цель статистического наблюдения, устанавливается объект и единица наблюдения, разрабатывается инструментарий, определяется круг признаков «характеризующих единицу наблюдения, по которым производится регистрация данных, разрабатывается программа статистического наблюдения , обосновывается вид и метод проведения наблюдения, разрабатывается инструкция для заполнения бланков
Программа стат иссл – содержит конкретные вопросы, на которые необходимо дать ответ в статистическом формуляре
Объект наблюдения совокупность социально — экономических процессов, подлежащих обследованию.
Единица наблюдения – элемент совокупности, по которому собирается необходимые данные
Критический момент – момент, по состоянию, на которое собирается информация
Методы контроля — Счетный (арифметический) – повторение расчетов и проверка итоговых сумм, четко устанавливается наличие ошибок. Может выполнятся непрофессионалами. Логический проводится путем сопоставления данных с данными прошлых периодов, по аналогичным объектам, территориям, по разноименным показателям, относящимся к одному объекту. Выполняется профессионалами.
Ошибки — По источнику происхождения(преднамеренные (злостные), непреднамеренные) По характеру:(случайные, систематические, презентативности (представительности)
Случайные ошибки — регистратора, небрежность в заполнении документации, неточность измерительных приборов, использование неверных формул средних и индексов Данные ошибки имеют свойство взаимопогашаться

Систематические ошибки — погрешности измерительных приборов, округление данных, забывчивость опрашиваемых и т.п. Данные ошибки имеют свойство накапливаться Сводка статистических данных — систематизация и обобщение материалов статистического наблюдения, подсчет числа единиц в группах и подгруппах, выделенных при группировке, и подведение итогов по количественным признакам ГРУППИРОВКА СТАТИСТИЧЕСКИХ ДАННЫХ — это расчленение единиц статистической совокупности на группы, однородные в каком – либо существенном отношении. Различают три вида группировки в зависимости от решаемых ими задач Задачи статистической группировки- 1 задача. Разделение совокупности на качественно однородные группы – выявление социально-экономических типов. Это группировки типологические (например, предприятий по формам собственности, продукции по видам, населения по социальным группам и т.п.) 2 задача. Характеристика структуры явления и структурных сдвигов. Это структурная группировка. Например, изучение структуры населения по полу, возрасту и т.п. 3 задача. Изучение взаимосвязей между отдельными признаками изучаемого явления. Такие группировки называются аналитическими (например, группировка рабочих по нормам выработки для установления влияния на размер заработной платы)

Разновидности группировочных признаков – атрибутивный, количественный

Относительная величина координации — соотношение между частями ( i, j, …) целого. В качестве базы сравнения принимается значение показателя, преобладающего в общем объеме совокупности.

Относительная величина наглядности — Соотношение одноименных показателей, относящихся к одному и тому же периоду (моменту) времени, но по разным объектам или территориям (a,b)
Относительные величины интенсивности — Являются именованными числами и показывают итог числителя, приходящийся на одну, десять или сто единиц показателя. Например, производительность труда
Средняя величина — обобщающий показатель, характеризующий типичный уровень варьирующего (изменяющегося) количественного признака на единицу совокупности в определенных условиях места и времени
Условия расчета средних 1)Расчет должен осуществляться по качественно однородной совокупности2)Для исчисления средних должны быть использованы массовые данные Средняя величина именована, т.е. имеет ту же единицу измерения, что и осредняемый показатель

Свойства средней арифметической 1. Сумма отклонений индивидуальных значений признака от средней арифметической равна 0. 2. Если все осредняемые варианты уменьшить или увеличить на постоянное число А, то средняя арифметическая уменьшится или увеличится на эту же величину. 3. Если все варианты значений признака уменьшить или увеличить в А раз, то средняя также соответственно уменьшится или увеличится в А раз. 4. Если все веса уменьшить или увеличить в А раз, то средняя арифметическая не изменится. Вариация — колеблемость, многообразие, изменяемость величины признака у единиц совокупности Ряды показателей:первичные;ранжированные, вариационные Первичный ряд

i	1	2	3	…	n
xi	x1	x2	x3	…	xn

Дискретный ряд i=1…k

xi	x1	x2	x3	…	n
ni	n1	n2	n3	…	xn

xi-1—xi	x0-x1	x1-x2	x2-x3	…	xk-1-xk
ni	n1	n2	n3	…	nk

Динамический ряд -это ряд показателей, изменяющихся во времени y1 y2 y3 … yn –- уровни динамического ряда Виды рядов: моментные(на определенную дату); интервальные(в каком-либо году) Расчет цепных и базисных показателей динамики: абсолютный прирост, относ прирост, темп прироста – отношение абсолютного прироста к абсолютному уровню, принятому за базу (к предыдущему уровню ряда), Абсолютное значение одного % прироста –отношение абсолютного прироста к темпу прироста

1. Расчет среднего абсолютного уровня

для интервального ряда

а) с равноотстоящими уровнями (yi – уровни ряда,n – число интервалов)

для моментного ряда

а) с равноотдаленными моментами в случае периодического учета пользуются формулой средней хронологической (n-число моментов учета):

для моментного ряда

с неравноотдаленными моментами в случае непрерывного учета:

для моментного ряда

с неравноотдаленными моментами в случае периодического учета пользуются формулой средней хронологической взвешенной

Расчет среднего абсолютного прироста

Расчет среднего темпа роста

а) для интервального ряда с равными интервалами (Tpi – цепные темпы роста k – число цепных темпов n – число интервалов времени)

Укрупнение интервалов динамического ряда. Первоначальный ряд динамики преобразуется и заменяется другим, показатели которого относятся к большим по продолжительности периодам времени. Вновь созданный ряд может содержать либо абсолютные величины за укрупненные по продолжительности промежутки времени (получается путем суммирования уровней первичного ряда абсолютных величин), либо средние величины.

Метод скользящей средней. Суть метода заключается в замене абсолютных данных средними арифметическими за определенные периоды. Расчет средних ведется способом скольжения, т.е. постепенным исключением из принятого периода скольжения первого уровня и включением следующего. При этом предварительно выбирают интервал сглаживания (обычно нечетное число уровней – 3,5,…). Расчет удобно представить в таблице.

Аналитическое выравнивание динамических рядов Основное содержание данного метода заключается в том, что основная тенденция развития ytрассчитывается как функция времени: yti = f(ti)Определение теоретических (расчетных) уровней yti производится на основе адекватной математической функции, которая наилучшим образом отображает тенденцию ряда динамики.

Формулы по статистике

Группировка статистических данных и ее роль в анализе информации_ 2

Абсолютные, относительные, средние величины_ 2

Относительные величины_ 2

Средние величины_ 2

Статистические распределения и их характеристики_ 3

Показатели вариации (колеблемости) признака_ 4

Сложение дисперсий_ 4

Показатель асимметрии_ 5

Показатель эксцесса (островершинности) 5

Кривые распределения 5

Выборочное наблюдение 6

Формулы ошибок простой случайной выборки_ 7

Формулы для определения численности простой и случайной выборки_ 7

Типичная выборка_ 7

Серийная выборка_ 8

Малые выборки_ 8

Корреляционная связь_ 8

Уравнение регрессии_ 9

Ряды динамики_ 10

Показатели динамики_ 10

Средние показатели динамики_ 10

Семестр 2 (Индексы) 11

Группировка статистических данных и ее роль в анализе информации

Абсолютные, относительные, средние величины

Относительные величины (ОВ) динамики характеризуют изменение явления во времени. (Коэффициент роста)

ОВ координации отражают отношение численности двух частей единого целого, т. е. показывают, сколько единиц одной группы приходится в среднем на одну, на 10 или на 100 единиц другой изучаемой совокупности.

ОВ наглядности (сравнения) отражают результаты сопоставления одноименных показателей, относящихся к одному и тому же периоду времени, но к разным объектам или территориям (например, сравнивается годовая производительность труда по 2-м предприятиям)

Степенные средние общего типового расчета:

Медиана – значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части.

Квартель

Дециль

Показатели вариации (колеблемости) признака

Среднее линейное отклонение – на сколько в среднем отличаются индивидуальные значения признака от среднего его значения.

Среднее квадратическое отклонение

Дисперсия

Коэффициент вариации (используется для характеристики однородности совокупности по исследуемому признаку)

Сложение дисперсий

Корреляционное отношение

Критерий согласия К. Пирсона ( Для проверки близости теоретического и эмпирического распределений, для проверки соответствия эмпирического распределения закону нормального распределения)

Критерий согласия Романовского

Если к Критерий Колмогорова

Распределение Пуассона (теоретические частоты)

Выборочное наблюдение

N – объем генеральной совокупности

N – объем выборочной совокупности (число единиц, попавших в выборку)

Р – генеральная доля (доля единиц, обладающих данным признаком в генеральной совокупности)

W – выборочная доля

S – среднее квадратическое отклонение признака в выборочной совокупности.

Неравенство Чебышеба

Теорема Ляпунова

Дает количественную оценку ошибки. При неограниченном объеме из генеральной совокупности с Р расхождения выборочной и генеральной средней равна интегралу Лапласа

Р – гарантированная вероятность

T – коэффициент доверия, зависящий от Р

Средняя ошибка (n>30) при случайной повторной выборке:

При случайной бесповторной выборке:

Формулы ошибок простой случайной выборки

Способ отбора единиц

Средняя ошибка μ:

Предельная ошибка Δ:

Доверительные интервалы для генеральной средней –

Доверительные интервалы для генеральной доли –

Доверительная вероятность – функция от t, вероятность находится по приложению3

Способ отбора единиц

Численность выборки (n):

*В случае, когда частость w даже приблизительно неизвестна, в расчет вводят максимальную величину дисперсии доли, равную 0,25 (если w=0,5, то w(1-w)=0,25).

Применяется в тех случаях, когда из генеральной совокупности можно выделить однокачественные группы единиц (или однородные), затем из каждой группы случайно отобрать определенное число единиц в выборку.

Стандартная среднеквадратическая ошибка:

- средняя из внутригрупповых

Бесповторный отбор -

Отбор единиц при типичной выборке из каждой типичной группы:

Вместо случайного отбора единиц совокупности осуществляется отбор групп (серий, гнезд). Внутри отобранных серий производится сплошное наблюдение.

Средняя стандартная ошибка:

Для оценки однородности совокупности – коэффициент вариации по факторным признакам

Линейный коэффициент корреляции

Оценка существенности линейного коэффициента корреляции

A, b,c, d – частоты взаимного сочетания (комбинации) двух альтернативных признаков, n – общая сумма частот

Выработка - W = Q/T, W – выработка, Q – физический объем реализованной продукции/услуг, T – затраты живого труда (среднесписочная численность работников/рабочих)

Трудоемкость (показатель, обратный выработке) - t = 1/W = T/Q Трудоемкость характеризует величину затрат рабочего времени на единицу произведенной продукции.

Индекс динамики выработки переменного состава , определяющий отношение выработки отчетного периода к выработке базисного периода - Iw = W1/W0

Этот индекс характеризует изменение производительности труда под влиянием всех факторов, а именно: НТП, человеческого фактора (квалификация и т. п.) и др.

Индекс динамики трудоемкости - It = t1/t0

Индекс динамики трудоёмкости характеризует изменение трудоёмкости в отчетном периоде по сравнению с базисным, и его величина зависит от изменения трудоёмкости производимой продукции и от изменения объемов производства этой продукции.

IQ = IW * IT – система связанных индексов, которая позволяет определить влияние интенсивных и экстенсивных факторов на изменение объема продукции, услуг.

Влияние интенсивного (качественного) и экстенсивного (количественного) факторов на абсолютное изменение физического объема продукции/услуг. Под экстенсивным фактором обычно понимают абсолютное изменение основных фондов. Под интенсивным – абсолютное изменение показателя фондоотдачи.

Читайте также: