Все шпоры по механике





Описание книги "Техническая механика. Шпаргалка"
Описание и краткое содержание "Техническая механика. Шпаргалка" читать бесплатно онлайн.
Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.
Техническая механика. Шпаргалка
1. Аксиомы и понятие силы статики
Теоретическая механика – это наука о механическом движении твердых материальных тел и их взаимодействии. Механическое движение понимается как перемещение тел в пространстве и во времени по отношению к другим телам, в частности, к Земле.
Статика изучает условия равновесия тел под действием сил.
Кинематика рассматривает движение тел как перемещение в пространстве; характеристики тел и причины, вызывающие движение, не рассматриваются.
Динамика изучает движение тел под действием сил.
Сила – это мера механического взаимодействия материальных тел между собой. Взаимодействие характеризуется величиной и направлением, т. е. сила – это величина векторная, характеризующаяся точкой приложения, направлением (линией действия), величиной (модулем).
Силы, действующие на тело (или систему сил), делят на внешние и внутренние. Внешние силы бывают активные и реактивные. Активные силы вызывают перемещение тела, реактивные стремятся противодействовать перемещению тела под действием внешних сил.
Системой сил называют совокупность сил, действующих на тело.
Эквивалентная система сил – система сил, действующая так же, как заданная.
Уравновешенной (эквивалентной нулю) системой сил называется такая система, которая, будучи приложенной к телу, не изменяет его состояния.
Систему сил, действующих на тело, можно заменить одной равнодействующей, действующей так, как система сил.
Все теоремы и уравнения статики выводятся из нескольких исходных положений, называемых аксиомами.
Первая аксиома. Под действием уравновешивающей системы сил абсолютно твердое тело или материальная точка находятся в равновесии или движутся равномерно и прямолинейно (закон инерции).
Вторая аксиома. Две силы, равные по модулю и направленные по одной прямой в разные стороны, уравновешиваются.
Третья аксиома. Не нарушая механического состояния тела, можно добавить или убрать уравновешивающую систему сил (принцип отбрасывания системы сил, эквивалентной нулю).
Четвертая аксиома (правило параллелограмма сил). Равнодействующая двух сил, приложенных к одной точке, приложена к той же точке и является диагональю параллелограмма, построенного на этих силах как на сторонах.
Пятая аксиома. При взаимодействии тел всякому действию соответствует равное и противоположно направленное противодействие.
Следствие из второй и третьей аксиом. Силу, действующую на твердое тело, можно перемещать вдоль линии ее действия.
2. Связи и реакции связей
Все тела делятся на свободные и связанные.
Свободные тела – это тела, перемещение которых не ограничено.
Связанные тела – это тела, перемещение которых ограничено другими телами.
Тела, ограничивающие перемещение других тел, называют связями.
Силы, действующие от связей и препятствующие перемещению, называют реакциями связей. Реакция связи всегда направлена с той стороны, куда нельзя перемещаться.
Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей).
Связи делятся на несколько типов.
Связь – гладкая опора (без трения) – реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре.
Гибкая связь (нить, веревка, трос, цепь) – груз подвешен на двух нитях. Реакция нити направлена вдоль нити от тела, при этом нить может быть только растянута.
Жесткий стержень – стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня. Стержень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи.
Возможным перемещением точки называется такое бесконечно малое мысленное перемещение, которое допускается в данный момент.
Шарнирная опора. Шарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров.
Подвижный шарнир. Стержень, закрепленный на шарнире, может поворачиваться вокруг шарнира, а точка крепления может перемещаться вдоль направляющей (площадки). Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, так как не допускается только перемещение поперек опорной поверхности.
Неподвижный шарнир. Точка крепления перемещаться не может.
Стержень может свободно поворачиваться вокруг оси шарнира. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Ее изображают в виде двух составляющих: горизонтальной и вертикальной (Rx, Ry).
Под действием внешних сил в опоре возникают реактивная сила и реактивный момент Мz, препятствующий повороту.
Реактивная сила представляется в виде двух составляющих вдоль осей координат:
3. Определение равнодействующей геометрическим способом
Система сил, линии действия которых пересекаются в одной точке, называется сходящейся.
Необходимо определить равнодействующую системы сходящихся сил (F1; F2; F3;…; Fn), где n – число сил, входящих в систему.
В соответствии со следствиями из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными к одной точке.
Используя свойство векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил.
При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.
Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называется геометрическим.
Многоугольник сил строится в следующем порядке.
1. Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпал с началом последующего.
2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.
3. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.
Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.
Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.
Если в системе три силы, образуется треугольник сил.
Геометрическим способом пользуются, если в системе три силы. При решении задач на равновесие тело считается абсолютно твердым (отвердевшим).
Задачи решаются в следующем порядке.
1. Определить возможное направление реакций связей.
2. Вычертить многоугольник сил системы, начиная с известных сил, в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура).
3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.
4. Для уточнения определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.
4. Определение равнодействующей аналитическим способом
Проекция сил на ось определяется отрезком оси, отсекаемой перпендикулярами, опущенными на ось из начала и конца вектора.
Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением сил. Проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси.
Проекция силы на две взаимно перпендикулярные оси.
Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определим равнодействующую аналитическим способом. Выберем систему координат, определим проекции всех заданных векторов на эти оси. Складываем проекции всех векторов на оси х и у.
Уравновешенные силы:
Система сил, под действием которой свободное твердое тело может находится в покое, называется уравновешенной.
Аксиомы статики:
а) Аксиома о уравновешенных силах (о абсолютном твердом теле) - две одинаковые силы, приложенные к абс. твердому телу и действуют вдоль одной прямой в противоположных направлениях назыв. уравновешенными силами. б) Аксиома о прибавлении или вычитании уравновешенной системы сил - действие системы сил на твердое тело не меняется, если если прибавить к ней уравновешенные силы. в) Аксиома сложения сил - силы, которые действуют на точку, можно складывать как векторы или аналитично. г) Аксиома о опорах (связи) и их реакции - силы могут быть активными и пассивными. Первые стремятся вызвать ускорение матер. точек. Другие - ограничивают движение. Они возникают как реакции системы на движение или на действие активных сил. Движение матер. точек может быть свободным или ограниченным. Во втором случае тело или точка назыв. несвободной. Все, что ограничивает движение тел в пространстве называется опорой (связью). д) Аксиома о освобождении от связи (опоры) - механическое состояние системы материальных точек не изменится, если освободить ее от связей, меняя их силами, действие которых такое же, как и связей (опор). Эти силы назыв. реакциями связей - пассивные силы, которые направлены в противоположную сторону относительно ограничения движения.
Момент силы относительно точки.
Вращательный эффект силы характеризуется ее эффектом. Моментом силы относительно центра О называется величина, равная взятому с соотв. знаком произведению модуля силы на длину плеча.
Момент силы относительно оси.
Моментом силы относительно оси называется скалярная величина, равная моменту проэкции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью.
Пара сил, момент пары. Свойства пар сил.
Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абс. твердое тело. Моментом пары наз. величина, равная взятому с соотв. знаком произведению модуля одной из сил пары на ее плечо (Понятие момента силы связано с точкой, относительно к-рой берется момент. Момент пары определяется только ее моментом и плечом; ни с какой точкой плоскости эта величина не связана). Св-ва : сумма моментов сил пары относительно точки не зависит от выбора точки и всегда равняется моменту пары, Пара сил не имеет равнодействующей - нельзя уравновесить одной силой.
Сложение пар сил.
Система пар, лежащих в одной плоскости, эквивалентна одной паре, лежащей в той же плоскости и имеющей момент, равный алгебраической сумме моментов слагаемых пар.
Теорема Вариньона.
О моменте равнодействующей - момент равнодействующей плоской системы сходящихся сил относительно любого центра равен алгебраической сумме моментов слагаемых сил относительно того же центра.
Виды нагрузок.
а) Сосредоточенная, б) Рассредоточенная равномерная и неравномерная, в) Пара сил - момент.
Параллельный перенос сил. Приведение системы сил к одному центру.
Силу можно переносить в любую точку тела, к-рая называется точкой приведения, если прибавить при этом пару сил (в точку приведения).
Главный вектор и главный момент произвольной системы сил.
Все силы, которые действуют на тело можно привести к одной точке, при этом вместо сил имеем эквивалентную систему сил, которая состоит из главного вектора и главного момента (пара сил). Частные случаи приведения произвольной системы сил к одному центру - а) главный момент равен равнодействующей, если главный момент М=0, б) Fгол=0, Мгол<>0, в) Fгол<>0, Мгол<>0, Мгол перпендик. Fгол - плоская система сил. г) Мгол<>0 Fгол<>0 Мгол || Fгол - силовой винт. е) Fгол=0, Мгол=0 - равновесие тела.
Условия равновесия произвольной пространственной системы сил.
S - сумма, Мгол = S Мi(F) = 0; Fгол = S Fi = 0;
Написать проекции на все оси.
Условия равновесия произвольной плоской системы сил.
а)Одной проекции силы нет, зато есть один момент с индексом этой оси б) есть два момента - нет двух сил в) Все моменты равны нулю.
Формы условий равновесия. .
Центр параллельных сил - это точка приложения равнодействующей системы параллельных сил.
Центр тяжести однородного тела.
Центр тяжести плоской фигуры.
Трение скольжения, угол трения.
Закон Кулона-Амонтона - F=fN. Угол трения - это угол, тангенс к-рого равен коэффициенту трения - предельный угол силы к нормали пов-ти, чтобы тело поехало.
Кинематика:
Теоремы о скоростях.
а) Проекции скоростей (абсол. твердого тела) двух точек на прямую, которая проходит через них равны. б) Скорость любой точки складывается из скорости какой-либо другой точки, принятой за полюс, и скорости ее вращения вокруг этой точки.
Мгновенный центр скоростей. Связь скоростей точек с мгновенными радиусами при п.п.д.
МЦС - это точка в плоскости движения, скорость к-рой в данный момент времени равна нулю.
Способы определения мгновенного центра скоростей.
Динамика точки и системы:
Основное уравнение динамики для свободной и несвободной материальной точки в векторной, координатной и естественной формах.
Теорема – о независимом действии сил – если на точку действует несколько сил или равнодействующая то точка будет двигаться с ускорением = сумме ускорений, к-рые возникают при действии каждой силы отдельно.
Вывести и сформулировать принцип Даламбера для точки.
ma = F + N; F + N + (-ma) = 0; Ф = -ma; - сила инерции.
Решение второй задачи динамики точки.
Это - зная силы найти закон движения. а) Показываем начальное и конечное положение тела. б) Направляем ось х из начального в конечное положение, ось у – перпендикулярно х с начального положения, в) Показываем тело в свободном положении и действующие на него силы, г) составляем дифур движения точки в проекции на ось х, д) интегрируем это уравнение, е) находим постоянные интегрирования с начальных условий и неизвестные величины. That all.
Две основные меры механического движения точки.
Импульс (кол-во движения) и кинетическая энергия.
Работа силы, когда тело вращается.
Теорема об изменении кинетической энергии точки.
Изменение кинетической энергии точки при некотором ее перемещении равно сумме работ внешних сил, которые действуют на этом перемещении на точку.
Идеальные связи – сумма возможных работ реакций которых равна нулю.
Возможные перемещения, возможная работа силы.
Возможное перемещение – это бесконечно малые перемещения точек мех. системы, которые мы представляем и которые разрешены связями. Возможные работы находятся по таким же правилам как и действительные, но вместо дифференциалов записываются их вариации.
Принцип Лагранжа-Даламбера (Общее уравнение динамики)
Связи, классификация связей.
а) геометрические (без производных), б) кинематические (дифференциальные rj’=V), в) интегрируемые (это кинемат. К-рые можно привести к геометрич. rj=s), г) односторонние, д) двухсторонние, е) нестационарные –f(t).
Принцип возможных перемещений.
Необходимыми и достаточными условиями для равновесия мех. системы, к которой приложены двусторонние, стационарные и идеальные связи, есть равенство нулю суммы возможных работ всех активных сил на любых возможных перемещениях из положения равновесия.
Обобщенные координаты, скорости, силы.
Обобщенная сила – это коэффициент при вариации обобщенной координаты в выражении возможной работы.
- Заговоры (15)
- Нумерология (11)
- Мудры (8)
- Обряды (4)
- Фотошоп (3)
- Фоны (1)
- Юмор (3)
- Ритуал (2)
- Льготы (1)
- Поиск пропавших (1)
- Купить (1)
- Оракул "Мудрые ответы на вечные вопросы" (1)
- Интерактивная 3D модель Вселенной (1)
- Гадания (97)
- Детям (72)
- Запоминалки (16)
- Поделки (11)
- Шпаргалки (6)
- Обучалки (6)
- Библиотека (6)
- ЕГЭ (3)
- ГДЗ (2)
- Самоучители (1)
- Переводчик (1)
- Здоровье (44)
- Нетрадиционно (10)
- Красота (10)
- Диагностика (6)
- Рецепты (2)
- Справочники (2)
- Народная медицина (1)
- Игры (1)
- Интересно (107)
- Гороскоп (33)
- Техники (11)
- Магия (8)
- 10 минут магических заклинаний (Александер Скай) (4)
- Мантры (4)
- Сюрприз (2)
- Луна (2)
- Замки из бумаги (1)
- Интерьер (25)
- Строим (9)
- Украшаем (6)
- ИНТЕРЬЕРНЫЕ СТИЛИ (3)
- Картинки (24)
- Магический квадрат (6)
- Музыка (10)
- Обереги (51)
- Куклы (13)
- Амулеты, талисманы (12)
- Отдых (14)
- Пейзаж (3)
- ПК (17)
- Религия (39)
- Молитвы (20)
- Святые (2)
- Ангелы (2)
- Сны Пресвятой Богородицы (1)
- Святые места (1)
- Рецепты (27)
- Ритуал (16)
- Денежные (5)
- Снятие порчи (3)
- Праздничные (2)
- Рукоделье (71)
- Вышивка (15)
- Украшения (7)
- Вязание крючком (9)
- Вязание спицами (6)
- Поделки (28)
- Руны (89)
- Значение рун (4)
- Ссылки (20)
- Стихи (8)
- Тест (103)
- Новый Акрополь (3)
- Кокология (3)
- Хиромантия (4)

Шпаргалки по физике. Здесь мы собрали лучшие шпаргалки по физике. Значения всех фундаментальных констант, абсолютно все формулы механики, молекулярной физики, электричества, теории волн, оптики. Самый полный справочник по формулам физики. Лучше просто не бывает
При изучении физики приходится сталкиваться с огромным количеством формул, без знания которых немыслимо решение задач по физике. Все формулы физики запомнить практически не возможно и важно знать, где найти ту или иную формулу. В учебнике по физике формулы размещены по соответствующим разделам среди текстовой информации, поэтому поиск формул там может занять большее время, чем в сети Интернет. Достаточно ввести в строку поиска "Формулы по физике" или такие конкретные запросы, как "Законы Ньютона" или "Закон всемирного тяготения" – и поисковик выдаст все сайты, содержащие необходимые Вам формулы.
Представленные ниже шпаргалки содержат очень много формул по физике, поэтому для Вашего удобства мы приводим список шпаргалок, которые есть в разделе. Щелкните по названию шпаргалки с формулами по физике для быстрого перехода к ее описанию и ссылки для скачивания. Итак, лучшие шпаргалки по физике на наш взгляд:
1. Физика. Все формулы (абсолютно все формулы физики)
2. Основные формулы физики (только основные физические формулы)
Данная шпаргалка включает в себя все формулы по физике, которые изучаются в средней школе. Надо отметить, что многие из них могут не разбираться на уроках физики в обычных классах, однако в классах с физико-математическим уклоном они встречаются. Так или иначе, любой школьник найдет в этой шпаргалке нужную формулу. Также эта шпаргалка, включающая все физические формулы, будет очень полезна студентам младших курсов.

Скачать шпаргалку (1.4 Мб, формат .doc)
Данная шпаргалка по физике включает в себя формулы физики по следующим темам:
- Фундаментальные константы
- Система единиц
- Механика
- Кинематика
- Скорость и ускорение
- Равномерное движение
- Равнопеременное движение
- Криволинейное движение
- Вращательное движение
- Динамика и статика
- Первый закон Ньютона
- Второй закон Ньютона
- Третий закон Ньютона
- Основной закон динамики для неинерциальных систем отчета
- Силы разной природы
- Закон всемирного тяготения
- Сила трения
- Закон Гука
- Динамика и статика вращательного движения
- Закон сохранения импульса
- Потенциальная и кинетическая энергия. Мощность
- Закон сохранения энергии
- Кинематика
- Молекулярная физика. Свойства газов и жидкостей
- Уравнение состояния
- Уравнение состояния (уравнение Менделеева- Клайперона)
- Полная внутренняя энергия системы
- Основное уравнение молекулярно-кинетической теории
- Закон Дальтона для давления смеси газов
- Броуновское движение
- Среднеквадратичная скорость молекул
- Наиболее вероятная скорость молекул
- Средняя арифметическая скорость молекул
- Закон Максвелла для распределения молекул идеального газа по скоростям
- Среднее число соударений молекулы за 1 секунду
- Средняя длинна свободного пробега молекул
- Средний путь молекулы за время t
- Барометрическая формула
- Распределение Больцмана
- Термодинамика
- Первое начало термодинамики
- Работа газа
- Уравнение адиабаты
- Теплоемкость
- Тепловой баланс
- Тепловое расширение
- Тепловые машины
- Гидростатика, гидродинамика
- Давление на глубине
- Плотность
- Сила Архимеда
- Гидравлический пресс
- Закон сообщающихся сосудов
- Уравнение неразрывности
- Уравнение Бернулли
- Сила и энергия поверхностного натяжения
- Высота подъема жидкости в капилляре
- Уравнение состояния
- Электрические и электромагнитные явления
- Электростатика
- Закон Кулона
- Напряженность электрического поля
- Принцип суперпозиции полей
- Теорема Гаусса
- Теорема о циркуляции
- Потенциал
- Электроемкость уединенного проводника
- Плоский конденсатор
- Электроемкость заряженного шара
- Электроемкость сферического конденсатора
- Батарея конденсаторов
- Дипольный момент
- Поляризованность диэлектрика
- Диэлектрическая восприимчивость
- Диэлектрическая проницаемость
- Теорема Гаусса для диэлектриков
- Электродинамика. Постоянный ток
- Закон Ома
- Закон Джоуля–Ленца
- Правило Кирхгофа для узлов
- Правило Кирхгофа для контуров
- Параллельное соединение проводников
- Последовательное соединение
- Законы электролиза
- Первый закон Фарадея
- Второй закон Фарадея
- Электромагнетизм
- Сила Лоренца
- Сила Ампера, действующая на проводник длиной l
- Магнитная индукция поля в точке
- Магнитная индукция в центре витка
- Индукция внутри соленоида
- Индукция поля проводника на расстоянии R от оси
- Связь между магнитной индукцией и напряженностью магнитного поля
- Принцип суперпозиции магнитных полей
- Сила взаимодействия двух проводников
- Магнитный поток
- Энергия магнитного поля
- ЭДС индукции в замкнутом контуре
- ЭДС самоиндукции
- Электростатика
- Колебания и волны. Оптика. Акустика
- Механические и электромагнитные колебания
- Уравнение гармонических колебаний
- Полная энергия колеблющейся точки
- Сложение колебаний
- Затухающие колебания
- Переменный ток
- Импеданс цепи
- Упругие волны
- Скорость волны в газе, в твердом теле
- Уравнение плоской волны
- Интерференция
- Фазовая v и групповая u скорости
- Эффект Доплера
- Электромагнитные волны
- Фазовая скорость
- Оптика
- Разность хода
- Скорость света в среде
- Закон преломления
- Формула линзы
- Увеличение линзы
- Механические и электромагнитные колебания
- Квантовая физика и теория относительности
- Энергия фотона
- Фотоэффект
- Полная энергия
- Атомная физика
- Закон распада
Шпаргалка "Основные формулы физики" включает в себя формулы, которые наиболее часто используются при решении задач по физике. Здесь нет экзотических физичеких формул, которые не изучаются в школе, равно как и нет формул по физике, которые используются только при углубленном изучении предмета. Однако в большинстве случаев этих формул достаточно для решения базовых школьных задач по физике. Формулы набраны понятным, четким шрифтом, каждая тема в отдельной табличке. Можно распечатать и разрезать, очень удобно.

Скачать шпаргалку (0.1 Мб, формат .gif)
Данная шпаргалка по физике включает в себя формулы по физике на следующие темы:
- Кинематика
- Динамика
- Законы сохранения
- Механика жидкостей
- Колебания и волны
- Основы МКТ
- Термодинамика
- Оптика
- Электростатика
- Постоянный ток
- Электромагнитные колебания
- Индукция
- Квантовая физика
- Ядерные реакции
- Основы СТО
Более 2000 тестов с видео-решениями по математике. Более 1000 - по физике.
Подготовка к ЕГЭ. Подготовка к ОГЭ (бывший ГИА).
Формулы, теоремы, решение типовых заданий…
На нашем WiKi-справочнике есть разделы по: геометрии, стереометрии, алгебре, физике и др.
Проверьте себя самостоятельно!
Насколько хорошо Вы (или ваши дети) знают предмет?
А Вы готовы к контрольной?
Телефоны:
- +7 (910) 874 73 73
- +7 (905) 194 91 19
- +7 (831) 247 47 55







За одного скидка 15%
За двоих скидка 30%!
+7 (910) 874-73-73
Формулы по физике для ЕГЭ
Шпаргалка с формулами по физике для ЕГЭ
и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
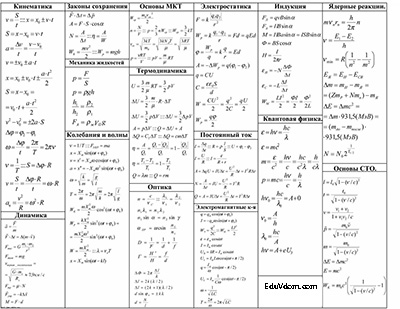
Для начала картинка, которую можно распечатать в компактном виде.
А потом вордовский файл, который содержит все формулы чтобы их распечатать, которые находятся внизу статьи.
Механика
- Давление Р=F/S
- Плотность ρ=m/V
- Давление на глубине жидкости P=ρ∙g∙h
- Сила тяжести Fт=mg
- 5. Архимедова сила Fa=ρж∙g∙Vт
- Уравнение движения при равноускоренном движении
X=X0+υ0∙t+(a∙t 2 )/2 S= (υ 2 -υ0 2 ) /2а S= (υ+υ0) ∙t /2
- Уравнение скорости при равноускоренном движении υ=υ0+a∙t
- Ускорение a=(υ-υ0)/t
- Скорость при движении по окружности υ=2πR/Т
- Центростремительное ускорение a=υ 2 /R
- Связь периода с частотой ν=1/T=ω/2π
- II закон Ньютона F=ma
- Закон Гука Fy=-kx
- Закон Всемирного тяготения F=G∙M∙m/R 2
- Вес тела, движущегося с ускорением а↑ Р=m(g+a)
- Вес тела, движущегося с ускорением а↓ Р=m(g-a)
- Сила трения Fтр=µN
- Импульс тела p=mυ
- Импульс силы Ft=∆p
- Момент силы M=F∙ℓ
- Потенциальная энергия тела, поднятого над землей Eп=mgh
- Потенциальная энергия упруго деформированного тела Eп=kx 2 /2
- Кинетическая энергия тела Ek=mυ 2 /2
- Работа A=F∙S∙cosα
- Мощность N=A/t=F∙υ
- Коэффициент полезного действия η=Aп/Аз
- Период колебаний математического маятника T=2π√ℓ/g
- Период колебаний пружинного маятника T=2 π √m/k
- Уравнение гармонических колебаний Х=Хmax∙cos ωt
- Связь длины волны, ее скорости и периода λ= υТ
Молекулярная физика и термодинамика
- Количество вещества ν=N/ Na
- Молярная масса М=m/ν
- Cр. кин. энергия молекул одноатомного газа Ek=3/2∙kT
- Основное уравнение МКТ P=nkT=1/3nm0υ 2
- Закон Гей – Люссака (изобарный процесс) V/T =const
- Закон Шарля (изохорный процесс) P/T =const
- Относительная влажность φ=P/P0∙100%
- Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
- Работа газа A=P∙ΔV
- Закон Бойля – Мариотта (изотермический процесс) PV=const
- Количество теплоты при нагревании Q=Cm(T2-T1)
- Количество теплоты при плавлении Q=λm
- Количество теплоты при парообразовании Q=Lm
- Количество теплоты при сгорании топлива Q=qm
- Уравнение состояния идеального газа PV=m/M∙RT
- Первый закон термодинамики ΔU=A+Q
- КПД тепловых двигателей η= (Q1 - Q2)/ Q1
- КПД идеал. двигателей (цикл Карно) η= (Т1 - Т2)/ Т1
Электростатика и электродинамика – формулы по физике
- Закон Кулона F=k∙q1∙q2/R 2
- Напряженность электрического поля E=F/q
- Напряженность эл. поля точечного заряда E=k∙q/R 2
- Поверхностная плотность зарядов σ = q/S
- Напряженность эл. поля бесконечной плоскости E=2πkσ
- Диэлектрическая проницаемость ε=E0/E
- Потенциальная энергия взаимод. зарядов W= k∙q1q2/R
- Потенциал φ=W/q
- Потенциал точечного заряда φ=k∙q/R
- Напряжение U=A/q
- Для однородного электрического поля U=E∙d
- Электроемкость C=q/U
- Электроемкость плоского конденсатора C=S∙ε∙ε0/d
- Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
- Сила тока I=q/t
- Сопротивление проводника R=ρ∙ℓ/S
- Закон Ома для участка цепи I=U/R
- Законы послед. соединения I1=I2=I, U1+U2=U, R1+R2=R
- Законы паралл. соед. U1=U2=U, I1+I2=I, 1/R1+1/R2=1/R
- Мощность электрического тока P=I∙U
- Закон Джоуля-Ленца Q=I 2 Rt
- Закон Ома для полной цепи I=ε/(R+r)
- Ток короткого замыкания (R=0) I=ε/r
- Вектор магнитной индукции B=Fmax/ℓ∙I
- Сила Ампера Fa=IBℓsin α
- Сила Лоренца Fл=Bqυsin α
- Магнитный поток Ф=BSсos α Ф=LI
- Закон электромагнитной индукции Ei=ΔФ/Δt
- ЭДС индукции в движ проводнике Ei=Вℓυsinα
- ЭДС самоиндукции Esi=-L∙ΔI/Δt
- Энергия магнитного поля катушки Wм=LI 2 /2
- Период колебаний кол. контура T=2π ∙√LC
- Индуктивное сопротивление XL=ωL=2πLν
- Емкостное сопротивление Xc=1/ωC
- Действующее значение силы тока Iд=Imax/√2,
- Действующее значение напряжения Uд=Umax/√2
- Полное сопротивление Z=√(Xc-XL) 2 +R 2
Оптика
- Закон преломления света n21=n2/n1= υ1/ υ2
- Показатель преломления n21=sin α/sin γ
- Формула тонкой линзы 1/F=1/d + 1/f
- Оптическая сила линзы D=1/F
- max интерференции: Δd=kλ,
- min интерференции: Δd=(2k+1)λ/2
- Диф.решетка d∙sin φ=k λ
Квантовая физика
- Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=Uзе
- Красная граница фотоэффекта νк = Aвых/h
- Импульс фотона P=mc=h/ λ=Е/с
Физика атомного ядра
- Закон радиоактивного распада N=N0∙2 - t / T
- Энергия связи атомных ядер
- t=t1/√1-υ 2 /c 2
- ℓ=ℓ0∙√1-υ 2 /c 2
- υ2=(υ1+υ)/1+ υ1∙υ/c 2
- Е = mс 2
Читайте также:


