Заказать шпоры для 9 класса по математике
Выберите шпаргалки












Заказ успешно принят.
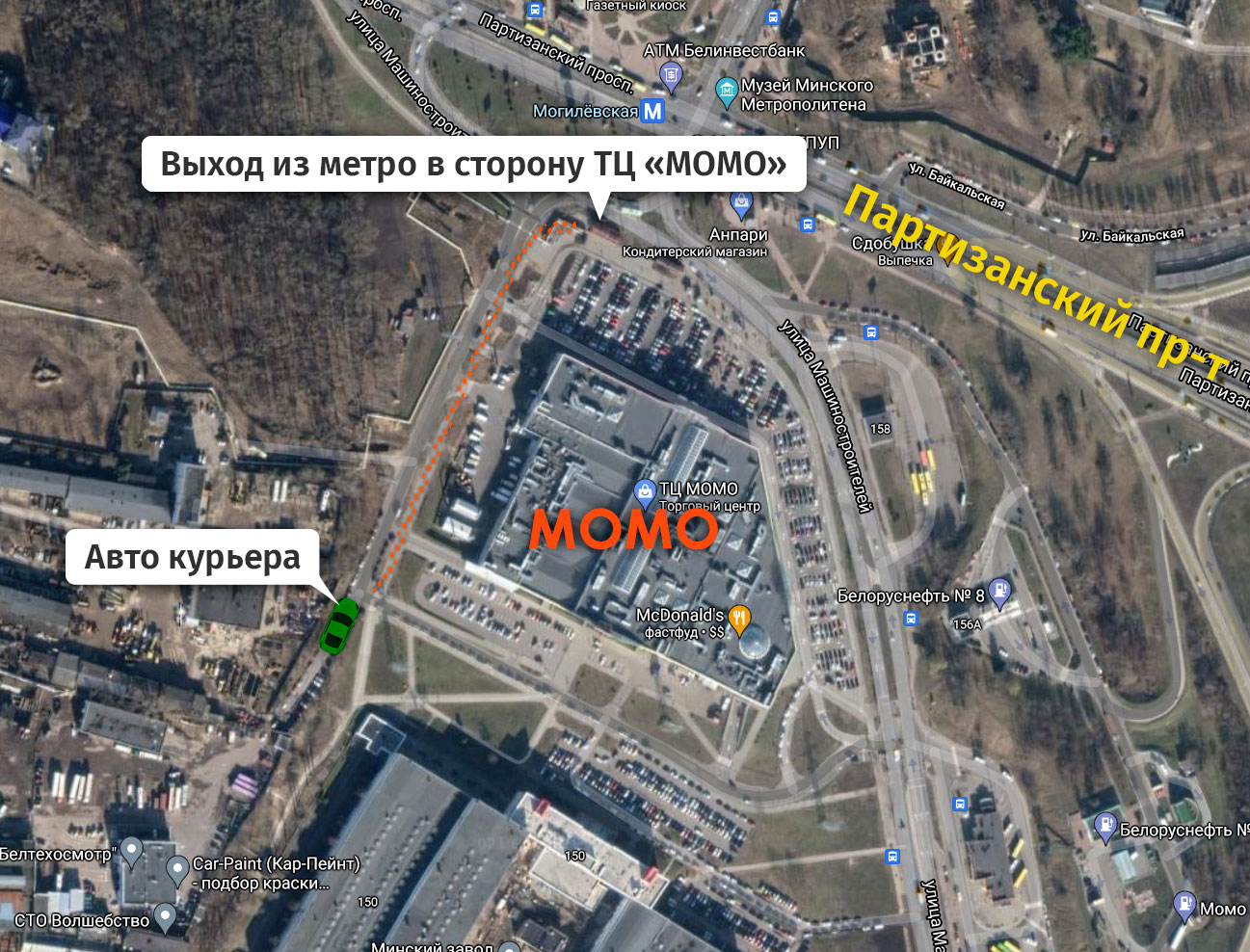
После этого вам нужно подъехать на ст.м. Могилёвская в выбранный день и подойти к точке, указанной на схеме (см. ниже), где будет стоять авто курьера. Если по каким-либо причинам вы не можете найти курьера, наберите его по номеру +375 29 6451262.
Выберите дату:
Схема: (нажмите для увеличения)
Если у вас есть промокод, введите его здесь.
Стоимость с учётом скидки — << priceDiscount | currency >> руб.
Стоимость пересылки — около 3-4 руб. Стоимость доставки — 10 руб.
Шаг 1. Вы оформляете заказ на нашем сайте.
Шаг 2. Заказ отсылаем в течение 48 часов после оформления. Затем посылка идет 2-3 дня в областные центры и 3-4 дня в остальные населённые пункты.
Шаг 3. После этого вы получаете смс на указанный при оформлении заказа номер со ссылкой на отслеживание вашей посылки.
Шаг 4. Когда посылка придёт в ваше почтовое отделение, на следующий день в ваш почтовый ящик придёт бумажное извещение. С извещением вам нужно подойти на вашу почту, захватив с собой паспорт, и вручить извещение работнику почты. Работник почты попросит внести соответствующую оплату и выдаст вашу посылку.
Шаг 1. Вы оформляете заказ на нашем сайте по Минску.
Шаг 3. Если не можете найти курьера, набираете его по номеру +375 29 6451262 и забираете шпаргалки.
Если по каким-либо причинам у вас не получается забрать шпоры в оговоренное время — сообщите нам, и мы подберём для вас другой день.
На этот вопрос мы постараемся ответить тезисно в четырёх блоках.
Оплата шпаргалок происходит только при их получении.
Печать на шпаргалках выполняется в типографии на профессиональном принтере с высокой чёткостью печати.
Естественно экзамены может сдать каждый ученик, но при этом сдать и не получить стресса могут разве что единицы. О вашем спокойствии на экзаменах позаботимся мы! У вас всегда будет под рукой хорошая подсказка.
Не стоит терять шанс получить оценку в аттестат немного выше, чем планирвоалось, ведь это поможет вам поступит в желаемый ВУЗ.
По Минску шпаргалки разносим курьером (бесплатно). Осуществляем доставку почтой в любой город Беларуси: Минск, Гродно, Могилёв, Брест, Витебск, Гомель и в другие города и посёлки РБ.
Шпоры для белорусских школ, актуальные на 2020 год. 9 и 11 классы, базовые и повышенные уровни. Доставляем почтой в любой город и по Минску. Материал в шпаргалках подготовлен на основе сборников, утверждённых Министерством образования в 2020 г.
Формулы, правила, свойства. Можно использовать для сдачи ЕГЭ и ОГЭ по математике.
Для начала шпаргалка в компактном виде:
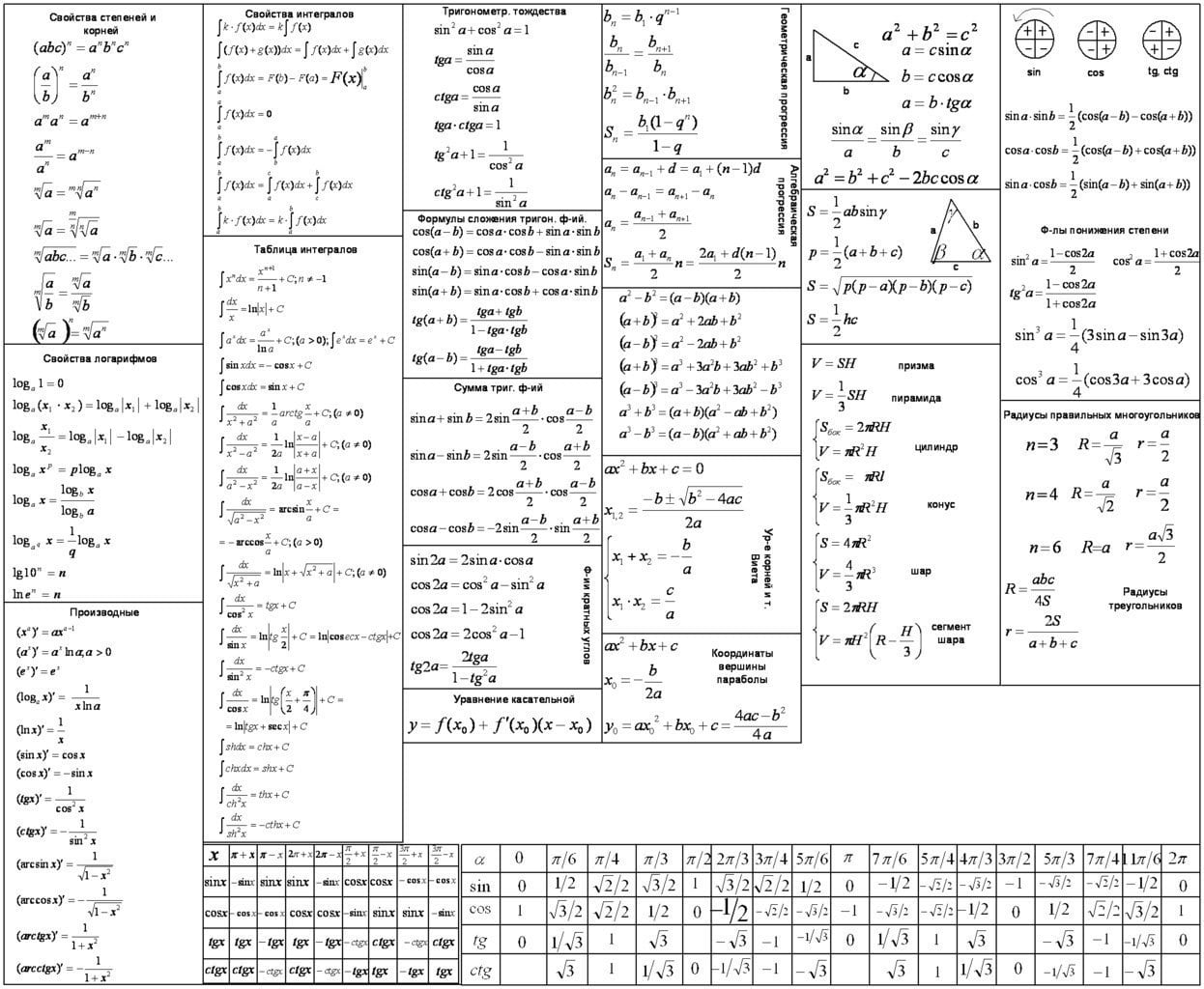
Формулы сокращенного умножения
(а+b) 2 = a 2 + 2ab + b 2
(а-b) 2 = a 2 – 2ab + b 2
a 3 – b 3 = (a-b)( a 2 + ab + b 2 )
a 3 + b 3 = (a+b)( a 2 – ab + b 2 )
(a + b) 3 = a 3 + 3a 2 b+ 3ab 2 + b 3
(a – b) 3 = a 3 – 3a 2 b+ 3ab 2 - b 3
Свойства степеней
a m/n = (a≥0, n ε N, m ε N)
a - r = 1/ a r (a>0, r ε Q)
a m · a n = a m + n
a m : a n = a m – n (a≠0)
Первообразная
Если F’(x) = f(x), то F(x) – первообразная
x n = x n +1 /n+1 + C
a x = a x / ln a + C
cos x = sin x + C
1/ sin 2 x = – ctg x + C
1/ cos 2 x = tg x + C
sin x = – cos x + C
Геометрическая прогрессия
q – знаменатель прогрессии
b n = b1 · q n – 1 – n-ый член прогрессии
Модуль
-a, если a Формулы cos и sin
sin (x + π) = -sin x
cos (x + π) = -cos x
sin (x + 2πk) = sin x
cos (x + 2πk) = cos x
sin (x + π/2) = cos x
Объемы и поверхности тел
1. Призма, прямая или наклонная, параллелепипед V = S·h
2. Прямая призма SБОК = p·h, p – периметр или длина окружности
3. Параллелепипед прямоугольный
V = a·b·c; P = 2(a·b + b·c + c·a)
P – полная поверхность
4. Куб: V = a 3 ; P = 6 a 2
S = 1/3 S·h; S – площадь основания
6. Пирамида правильная S =1/2 p·A
A – апофема правильной пирамиды
7. Цилиндр круговой V = S·h = πr 2 h
8. Цилиндр круговой: SБОК = 2 πrh
9. Конус круговой: V=1/3 Sh = 1/3 πr 2 h
10. Конус круговой: SБОК = 1/2 pL= πrL
Тригонометрические уравнения
sin x = 1, x = π/2 + 2 πn
sin x = -1, x = – π/2 + 2 πn
cos x = 0, x = π/2 + 2 πn
cos x = 1, x = 2πn
cos x = -1, x = π + 2 πn
Теоремы сложения
cos (x +y) = cosx ·cosy – sinx ·siny
cos (x -y) = cosx ·cosy + sinx ·siny
sin (x +y) = sinx ·cosy + cosx ·siny
sin (x -y) = sinx ·cosy – cosx ·siny
tg (x ±y) = tg x ± tg y/ 1 - + tg x ·tg y
ctg (x ±y) = tg x - + tg y/ 1± tg x ·tg y
sin x ± sin y = 2 cos (x±y/2)· cos (x - +y/2)
cos x ± cosy = -2 sin (x±y/2)· sin (x - +y/2)
1 + cos 2x = 2 cos 2 x; cos 2 x = 1+cos2x/2
1 – cos 2x = 2 sin 2 x; sin 2 x = 1- cos2x/2
a,b – основания; h – высота, c – средняя линия S = (a+b/2)·h = c·h
а – сторона, d – диагональ S = a 2 = d 2 /2
a – сторона, d1, d2 – диагонали, α – угол между ними S = d1d2/2 = a 2 sinα
9. Правильный шестиугольник
a – сторона S = (3√3/2)a 2
S = (L/2) r = πr 2 = πd 2 /4
Правила дифференцирования
( f (x) + g (x) )’ = f ’(x) + g’(x)
(tg x)’ = 1/ cos 2 x
(ctg x)’ = – 1/ sin 2 x
(f (kx + m))’ = kf ’(kx + m)
Уравнение касательной к графику функции
Площадь S фигуры, ограниченной прямыми x = a , x = b
Формула Ньютона-Лебница
| t | π/4 | π/2 | 3π/4 | π |
| cos | √2/2 | 0 | -√2/2 | 1 |
| sin | √2/2 | 1 | √2/2 | 0 |
| t | 5π/4 | 3π/2 | 7π/4 | 2π |
| cos | -√2/2 | 0 | √2/2 | 1 |
| sin | -√2/2 | -1 | -√2/2 | 0 |
| t | 0 | π/6 | π/4 | π/3 |
| tg | 0 | √3/3 | 1 | √3 |
| ctg | - | √3 | 1 | √3/3 |
sin x = b x = (-1) n arcsin b + πn
cos x = b x = ± arcos b + 2 πn
tg x = b x = arctg b + πn
ctg x = b x = arcctg b + πn
Теорема синусов : a/sin α = b/sin β = c/sin γ = 2R
Теорема косинусов : с 2 =a 2 +b 2 -2ab cos y
Неопределенные интегралы
∫ x n dx = (x n +1 /n+1) + C
∫ sin x dx = – cos x + C
∫ cos x dx = sin x + C
∫ dx/sin 2 x = -ctg + C
∫ dx/cos 2 x = tg + C
∫ x r dx = x r+1 /r+1 + C
Логарифмы
| Градус | 0 | 30 | 45 | 60 |
| sin | 0 | 1/2 | √2/2 | √3/2 |
| cos | 1 | √3/2 | √2/2 | 1/2 |
| tg | 0 | √3/3 | 1 | √3 |
| t | π/6 | π/3 | 2π/3 | 5π/6 |
| cos | √3/2 | 1/2 | -1/2 | -√3/2 |
| sin | 1/2 | √3/2 | √3/2 | 1/2 |
| 90 | 120 | 135 | 150 | 180 |
| 1 | √3/2 | √2/2 | 1/2 | 0 |
| 0 | -1/2 | -√2/2 | -√3/2 | -1 |
| - | -√3 | -1 | √3/3 | 0 |
| t | 7π/6 | 4π/3 | 5π/3 | 11π/6 |
| cos | -√3/2 | -1/2 | 1/2 | √3/2 |
| sin | -1/2 | -√3/2 | -√3/2 | -1/2 |
Формулы двойного аргумента
cos 2x = cos 2 x – sin 2 x = 2 cos 2 x -1 = 1 – 2 sin 2 x = 1 – tg 2 x/1 + tg 2 x
sin 2x = 2 sin x · cos x = 2 tg x/ 1 + tg 2 x
tg 2x = 2 tg x/ 1 – tg 2 x
ctg 2x = ctg 2 x – 1/ 2 ctg x
sin 3x = 3 sin x – 4 sin 3 x
cos 3x = 4 cos 3 x – 3 cos x
tg 3x = 3 tg x – tg 3 x / 1 – 3 tg 2 x
sin s cos t = (sin (s+t) + sin (s+t))/2
sin s sin t = (cos (s-t) – cos (s+t))/2
cos s cos t = (cos (s+t) + cos (s-t))/2
Формулы дифференцирования
x’ = 1 (sin x)’ = cos x
(kx + m)’ = k (cos x)’ = – sin x
(1/x)’ = – (1/x 2 ) ( ln x)’ = 1/x
(e x )’ = e x ; (x n )’ = nx n-1 ;(log a x)’=1/x ln a
Площади плоских фигур
1. Прямоугольный треугольник
S = 1/2 a·b (a, b – катеты)
2. Равнобедренный треугольник
S = (a/2)·√ b 2 – a 2 /4
3. Равносторонний треугольник
S = (a 2 /4)·√3 (a – сторона)
4. Произвольный треугольник
a,b,c – стороны, a – основание, h – высота, A,B,C – углы, лежащие против сторон; p = (a+b+c)/2
S = 1/2 a·h = 1/2 a 2 b sin C =
a 2 sinB sinC/2 sin A= √p(p-a)(p-b)(p-c)
a,b – стороны, α – один из углов; h – высота S = a·h = a·b·sin α
cos (x + π/2) = -sin x
Формулы tg и ctg
tg x = sin x/ cos x; ctg x = cos x/sin x
ctg (x + πk) = ctg x
ctg (x ± π) = ± ctg x
tg (x + π/2) = – ctg x
ctg (x + π/2) = – tg x
sin 2 x + cos 2 x =1
1 + tg 2 x = 1/ cos 2 x
1 + ctg 2 x = 1/ sin 2 x
tg 2 (x/2) = 1 – cos x/ 1 + cos x
cos 2 (x/2) = 1 + cos x/ 2
sin 2 (x/2) = 1 – cos x/ 2
P = 4 πR 2 = πD 2
V = πh 2 (R-1/3h) = πh/6(h 2 + 3r 2 )
SБОК = 2 πRh = π(r 2 + h 2 ); P= π(2r 2 + h 2 )
V = 1/6 πh 3 + 1/2 π(r 2 + h 2 )· h;
14. Шаровой сектор:
V = 2/3 πR 2 h’ где h’ – высота сегмента, содержащего в секторе
Формула корней квадратного уравнения
ax 2 + bx + c = 0 (a≠0)
Если D=0, то x = -b/2a (D = b 2 -4ac)
Если D>0, то x1,2 = -b± /2a
Арифметическая прогрессия
a n+1 = a n + d, где n – натуральное число
d – разность прогрессии;
a n = a 1 + (n – 1)·d – формула n-го члена
Радиус описанной окружности около многоугольника
R = a/ 2 sin 180/n
Радиус вписанной окружности
L = 2 πR S = πR 2
Площадь конуса
Тангенс угла - отношение противолежащего катета к прилещащему. Котангенс – наоборот.
Скачать шпаргалки по математике
Скачать всё это в компактном виде: matematika-shpory.doc.
Рекомендуем:

10. Нательные записи
Поистине безграничные возможности открываются перед девочками, учитывая особенности их гардероба. Все видели картинки с исписанными сплошным синим текстом, который скрывается под юбкой, ногами. Более современный вариант, так сказать, ноу-хау последнего времени – маникюр со шпаргалками. Одним словом, поле для творчества есть, нужно осваивать.
Плюсы: несложно пронести с собой, легко спрятать, высокая вероятность списать.
Плюсы: высокая эффективность.
Минусы: воспользоваться можно лишь в случаях, когда известны все вопросы билета; трудно применить в случае написания работы на листах с гербовой печатью.
8. Игра в прятки
Плюсы: пронести шпаргалку точно удастся.
Минусы: по неумелости можно испортить обувь, не совсем удобно доставать.
7. Шпионские страсти
В этом тематическом блоке мы объединили несколько способов списывания с помощью технических устройств, которыми еще 10 лет назад пользовались только герои популярных телевизионных саг о шпионах. Сегодня же нижеперечисленными средствами никого не удивишь.
В предыдущих наших статьях мы уже упоминали о списывании с помощью маленького микронаушника. Последнее время набирают популярность и другие виды. Так наиболее простым (и наиболее дешевым) в данном отношении является ручка с невидимыми чернилами. Написанное ею через минуту пропадает, а увидеть текст можно только посветив на него специальным фонариком, который, как правило, находится на другом конце ручки.
Плюсы: высокая вероятность остаться незамеченным, эффективность, возможность работать с огромными базами данных.
Минусы: дороговизна, технические сбои, не повсеместная возможность применения.
6. Мини-шпаргалка
Во время многочисленных интервью с преподавателями и учителями относительно списывания, они довольно часто рассказывают о настолько маленьких шпаргалках, спрятанных в таких непредсказуемых местах, что поневоле восхищаешься. Нередки случаи написания томика шпаргалок с последующим их скрытием под видом женского перстня. Для этого сверху, в качестве обложки, применяется какой-нибудь популярный принт, из-за чего кольцо выглядит как украшение. Самому сделать такое довольно сложно (хотя и есть пошаговые инструкции), поэтому можно купить сразу готовый вариант.

(как сделать мини-шпаргалку самостоятельно)
Плюсы: преимущество 2в1 – и шпаргалка, и способ ее спрятать одновременно.
Минусы: тяжело сделать, маленький размер шпаргалок.
5. Канцелярские принадлежности
Плюсы: легко принести с собой, можно пользоваться, не скрываясь, при обнаружении есть вероятность понести не столь суровое наказание.
Минусы: трудоемкий процесс изготовления, ограничено место для шпаргалки.
4. Умные часы

Об этом техническом устройстве мы решили рассказать отдельно по ряду причин. Во-первых, чтобы еще раз отдать должное эпохе высоких технологий и ее влиянию на все сферы нашей жизни, включая списывание. Во-вторых, умные часы (англ. smart watch) являются предметом с которым многие, включая экзаменаторов, еще не знакомы. Грамотное использование такого предмета в качестве шпаргалки, с высокой долей вероятности гарантирует успешную сдачу.
Существуют и мобильные телефоны в форме наручных часов. Здесь набор функций еще больше, что создает дополнительные возможности для списывания.
Плюсы: эффективность, все преимущества технических шпаргалок, внешний вид, не вызывающий вопросов у преподавателя.
Минусы: стоимость, работают в синхронизации с современными мобильными устройствами.
3. Ручка с ответами
Под означенным заголовком скрывается довольно любопытный единичный случай, который мы, исходя из его уникальности, решили вынести отдельным пунктом и тем самым воздать должное человеческой изобретательности и находчивости.
На одном из экзаменов, двое молодых людей решили списать довольно оригинальным способом. Они купили 60 одинаковых шариковых ручек, на их колпачках написали номера билетов, а на самих ручках нацарапали ответы на вопросы. Все что требовалось дальше – иметь хорошее зрение и достать нужную ручку с рюкзака. Казалось бы, идея не новая, но ее практическая реализация и требуемая усидчивость, как минимум, заслуживают высокой оценки.
Плюсы: эффективность, незаметность.
Минусы: трудоемкость.
2. Бутылка газировки
К слову, сделать такую шпаргалку не так уж сложно. Смотрим инструкцию здесь и уповаем на то, что ее не видел ваш преподаватель.
Плюсы: оригинальность, а следовательно эффективность, легально можно взять с собой на экзамен, не вызвав подозрений.
Минусы: ограниченность пространства для нанесения шпаргалки.
Итак, мы подошли к первой позиции. Но чтобы сохранить еще ненадолго интригу, рекомендуем вам посмотреть это видео, в котором показаны некоторые из уже описанных оригинальных шпаргалок, а также собраны другие не менее интересные экземпляры.
1. Собственные знания
Желаем вам успехов во время сдачи экзаменов!
Отзывы и комментарии
Оценить материал, а также поделиться собственными идеями и знаниями в области изготовления и применения оригинальных шпаргалок, можно путем написания комментария в специальной форме ниже.
Шпаргалки по математике, алгебре и геометрии Шпаргалки по физике / Шпаргалки по химии
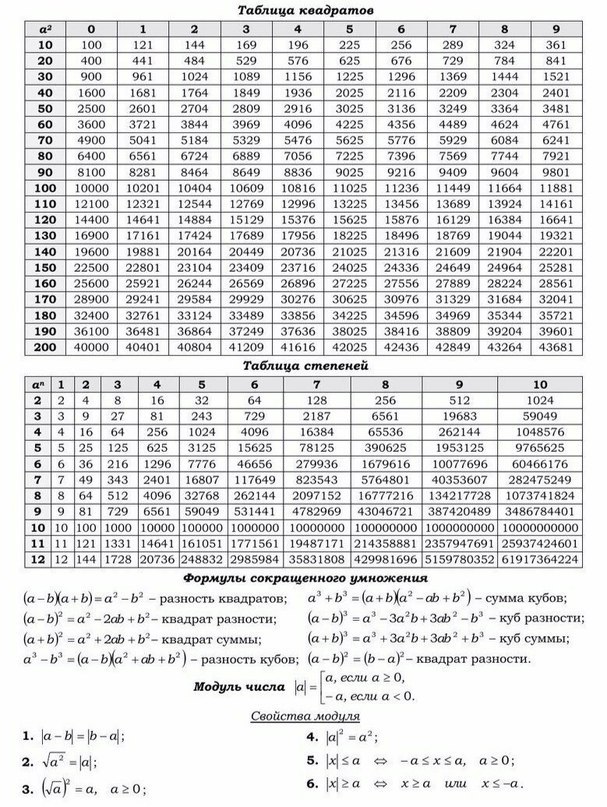
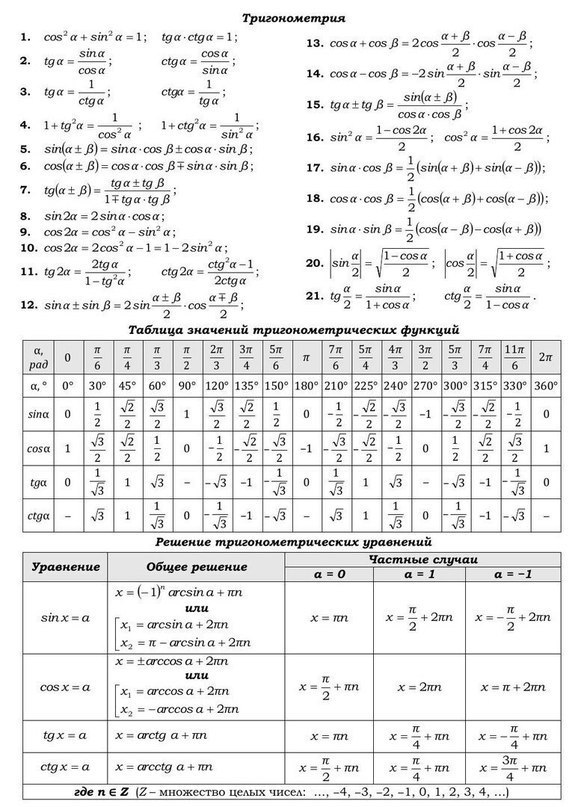
| Таблица квадратов. Таблица степеней. Формулы сокращенного умножения. Модуль числа. Свойства модуля: | Уравнения и неравенства с модулем. Последовательности и прогрессии. Метод кординат на плоскости. Скалярное произведение векторов. Расстояние между точками. | Тригонометрия - основные формулы. Таблица значений тригонометрических функций. Решение тригонометрических уравнений: | Четность и нечетность тригонометрических функций. Обратные тригонометрические функции. Формулы приведения. Знаки тригонометрических функций. Показательные уравнения и неравенства. |
 |  |  |  |
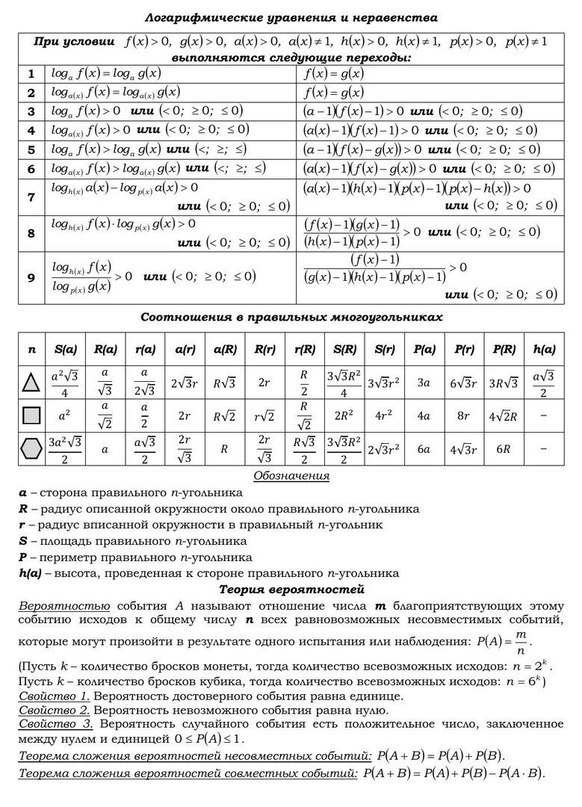
| Корень n-ой степени. Степени. Иррациональные уравнения и неравенства. Логарифм, свойства логарифмов | Логарифмические уравнения и неравенства. Соотношения в правильных многоугольниках. Теория вероятностей. Теоремы сложения вероятностей. | Логарифмические уравнения и неравенства. | Производная. Правила дифференцирования. Производная сложной функции. Уравнение касательной к графику функции в точке. |
 |  |  |  |
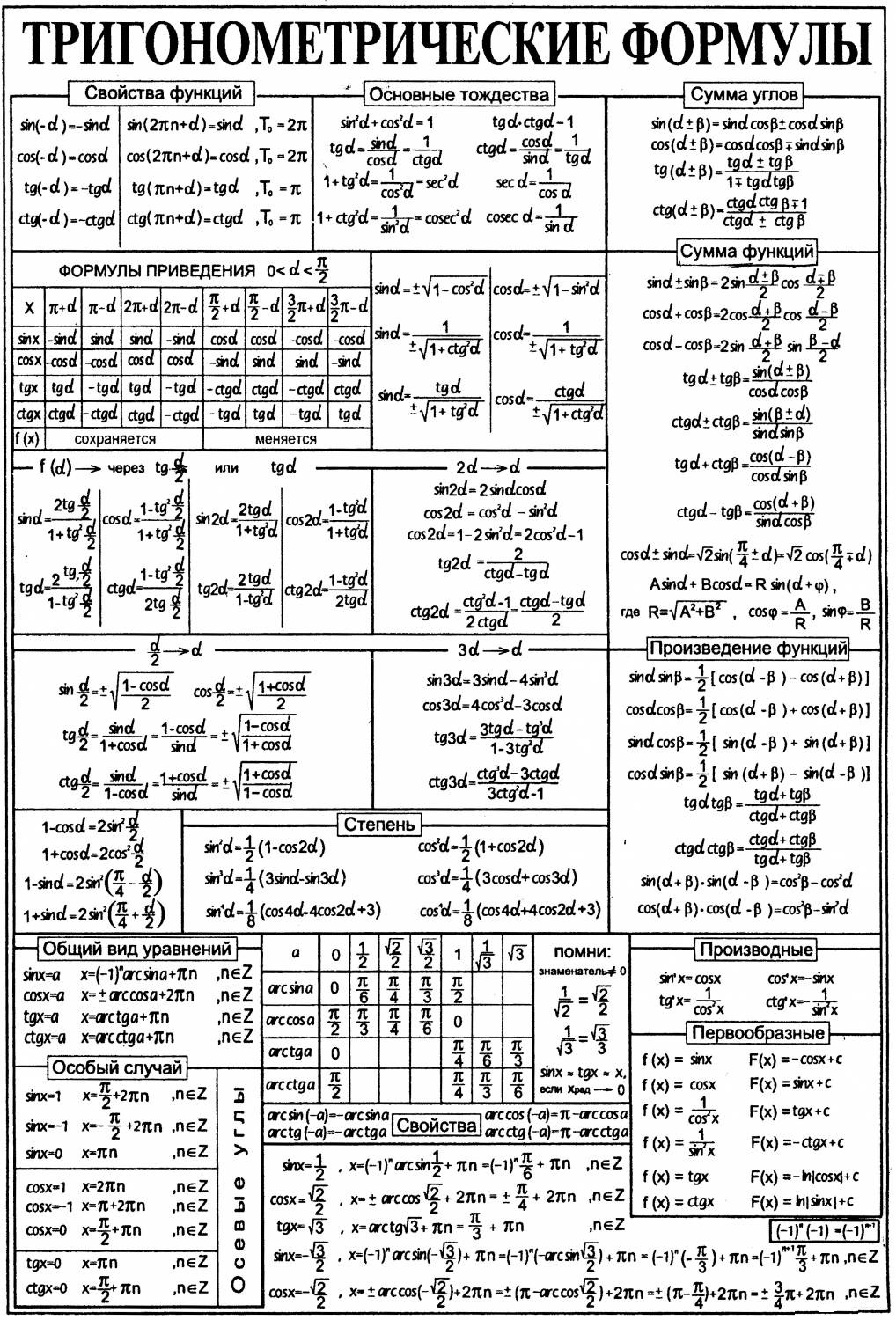
| Тригонометрические формулы. Свойства функций, основные тождества, сумма углов. Сумма функций, формулы приведения, особые случаи, степени, половинные, двойные и тройные углы. Обратные функции. | |||
 |
| Набор 2 - Алгебра. Линейная алгебра. | |||
| Свойства степеней. Формулы сокращенного умножения. Свойства арифметических корней. Модуль. Начала математического анализа: прогрессии арифметическая и геометрическая. Производная. Первообразная и интеграл. Среднее арифметическое и среднее геометрическое. | Тригонометрия. Основные формулы. Арксинус, арккосинус, арктангенс, арккотангенс. Четность функций. Значения тригонометрических функций некоторых углов. | Графики некоторых элементарных функций. Логарифмы. Решение квадратных, иррациональных, показательных, тригонометрических уравнений, уравнений с модулем | Квадратные неравенства. Неравенства с модулем. Логарифмические неравенства. Неравенства с модулем. Иррациональные неравенства. Показательные неравенства. Комбинаторика и бином Ньютона. |
 |  |  |  |
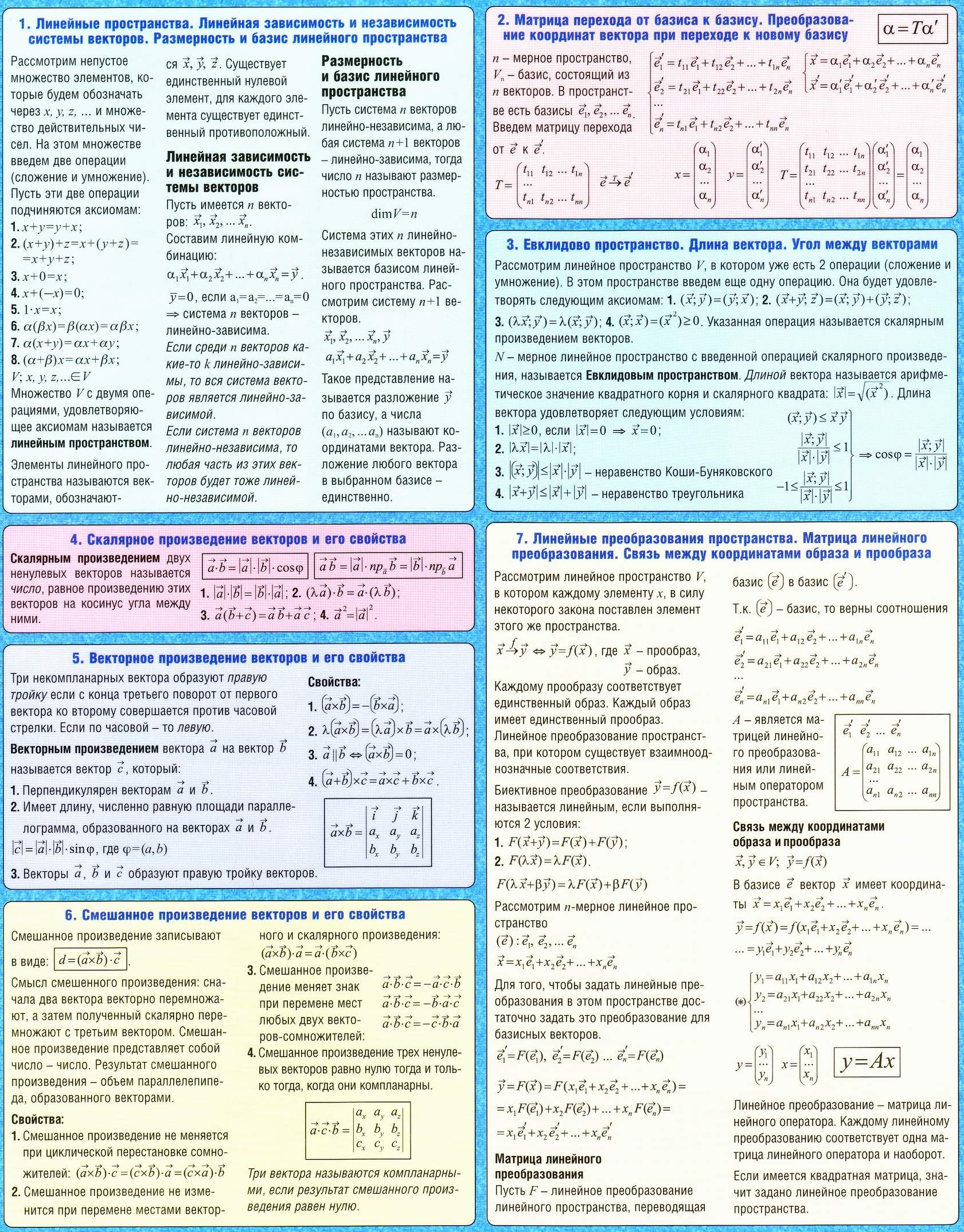
| Определение комплексного числа. Геометрическая интерпретация комплексного числа. Тригонометрическая форма комплексного числа. Показательная форма комплексного числа. Действия с комплексными числами. Последовательности, пределы последовательности. Теоремы о пределах числовых последовательностей. | Определение предела числовой функции. Односторонние пределы. Свойства пределов. Непрерывные функции и их свойства. Точки разрыва и их классификации. Замечательные пределы. Важные пределы. Теоремы о среднем. Правило Лопиталя. | Линейные пространства. Линейная зависимость и независимость системы векторов. Размерность и базис линейного пространства. Скалярное и векторное произведение векторов. Смешанное произведение векторов. Матрица перехода от базиса к базису. Преобразование координат вектора при переходе к новому базису. Евклидово пространство. Длина вектора. Угол между векторами. Линейные преобразования пространства. Матрица линейного преобразования. Связь между координатами образа и прообраза. | Связь между координатами одного и того же линейного оператора в разных базисах. Угол между прямой и плоскостью. Расстояние от точки до плоскости. Характеристические уравнения линейного оператора. Собственные векторы линейного оператора и их свтойства. Поверхности второго порядка. Плоскость в пространстве. Виды углов в пространстве. Уравнения плоскости. |
 |  |  |  |
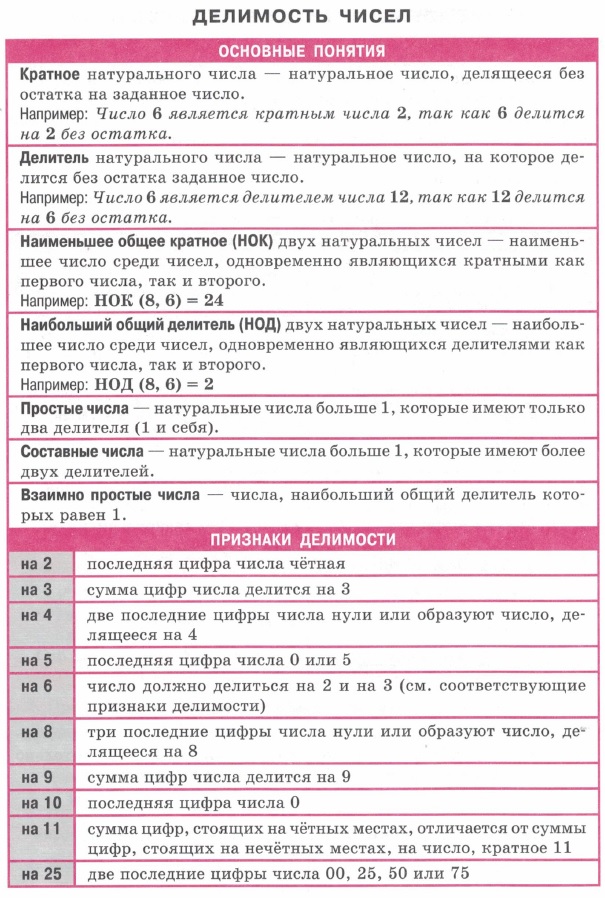
| Делимость чисел. Кратное. Делитель. НОК. НОД Простые и составные числа. Взаимно простые числа. | Числовые последовательности, члены, способы задания. Арифметическая и геометрическая прогрессии. Формулы. Характеристические свойства | Числа. Множества натуральных, целых, рациональных, действительных, иррациональных чисел. Арифметические действия с дробями. Модуль - свойства. | Решение квадратных уравнений. Формулы дискриминанта. Решение неполных квадратных уравнений. Теорема Виета. Алгоритм решения квадратного неравенства. |
 |  |  |  |
| Основные свойства функций. Понятие функции. Четность и нечетность. Периодичность. Нули функции. Промежутки знакопостоянства. Монотонность (возрастание, убывание). Асимптоты. Алгоритм описания фукнкции. |
Преобразование графиков функций у= f(x) в y=-f(x); y=f(-x); y=-f(-x); y=f(x-a); y=f(x)+b; y=f(ax); y=kf(x); y=|f(x)|; y=f(|x|). Построение графика обратной функции Степенные функции y=xn и y=x1/n, n∈Z. Свойства, графики. Квадратичная функция. Свойства степеней. Свойства арифметических корней. Формулы сокращенного умножения. Примеры значения степенных функций. Неравенства, понятия, строгие, нестрогие, решение. Свойства неравенств. Решение линейных неравенств. Решение квадратных неравенств. Метод интервалов при решении неравенств. Решение показательных неравенств. Решение логарифмическмх неравенств. Решение иррациональных неравенств. Решение неравенств с модулем. Часто применяемые неравенства Интегрирование функций. Понятие и основное свойство первообразной. Неопределенный интеграл. Правила интегрирования. Определенный интеграл. Формула Ньютона-Лейбница. Свойства и геометрический смысл определенного интеграла. Физический смысл определенного интеграла Уравнения прямой на плоскости. Общее уравнение прямой. Уравнение прямой "в отрезках". Уравнение прямой с угловым коэффициентом. Уравнение пучка прямых, проходящих через точку. Уравнение прямой, проходящей через 2 точки. Нормальное уранение прямой. Консультации и техническая #математикаФормулы сокращенного умножения (а+b) 2 = a 2 + 2ab + b 2 (а-b) 2 = a 2 – 2ab + b 2 a 3 – b 3 = (a-b)( a 2 + ab + b 2 ) a 3 + b 3 = (a+b)( a 2 – ab + b 2 ) (a + b) 3 = a 3 + 3a 2 b+ 3ab 2 + b 3 (a – b) 3 = a 3 – 3a 2 b+ 3ab 2 - b 3 Свойства степеней a m/n = (a≥0, n ε N, m ε N) a - r = 1/ a r (a>0, r ε Q) a m · a n = a m + n a m : a n = a m – n (a≠0) Первообразная Если F’(x) = f(x), то F(x) – первообразная x n = x n +1 /n+1 + C a x = a x / ln a + C cos x = sin x + C 1/ sin 2 x = – ctg x + C 1/ cos 2 x = tg x + C sin x = – cos x + C Геометрическая прогрессия q – знаменатель прогрессии b n = b1 · q n – 1 – n-ый член прогрессии Модуль -a, если a 3 ; P = 6 a 2 S = 1/3 S·h; S – площадь основания 6. Пирамида правильная S =1/2 p·A A – апофема правильной пирамиды 7. Цилиндр круговой V = S·h = πr 2 h 8. Цилиндр круговой: SБОК = 2 πrh 9. Конус круговой: V=1/3 Sh = 1/3 πr 2 h 10. Конус круговой: SБОК = 1/2 pL= πrL Тригонометрические уравнения sin x = 1, x = π/2 + 2 πn sin x = -1, x = – π/2 + 2 πn cos x = 0, x = π/2 + 2 πn cos x = 1, x = 2πn cos x = -1, x = π + 2 πn Теоремы сложения cos (x +y) = cosx ·cosy – sinx ·siny cos (x -y) = cosx ·cosy + sinx ·siny sin (x +y) = sinx ·cosy + cosx ·siny sin (x -y) = sinx ·cosy – cosx ·siny tg (x ±y) = tg x ± tg y/ 1 - + tg x ·tg y ctg (x ±y) = tg x - + tg y/ 1± tg x ·tg y sin x ± sin y = 2 cos (x±y/2)· cos (x - +y/2) cos x ± cosy = -2 sin (x±y/2)· sin (x - +y/2) 1 + cos 2x = 2 cos 2 x; cos 2 x = 1+cos2x/2 1 – cos 2x = 2 sin 2 x; sin 2 x = 1- cos2x/2 a,b – основания; h – высота, c – средняя линия S = (a+b/2)·h = c·h а – сторона, d – диагональ S = a 2 = d 2 /2 a – сторона, d1, d2 – диагонали, α – угол между ними S = d1d2/2 = a 2 sinα 9. Правильный шестиугольник a – сторона S = (3√3/2)a 2 S = (L/2) r = πr 2 = πd 2 /4 Правила дифференцирования ( f (x) + g (x) )’ = f ’(x) + g’(x) (tg x)’ = 1/ cos 2 x (ctg x)’ = – 1/ sin 2 x (f (kx + m))’ = kf ’(kx + m) Уравнение касательной к графику функции Площадь S фигуры, ограниченной прямыми x=a, x=b Формула Ньютона-Лебница t π/4 π/2 3π/4 π cos √2/2 0 -√2/2 1 sin √2/2 1 √2/2 0 t 5π/4 3π/2 7π/4 2π cos -√2/2 0 √2/2 1 sin -√2/2 -1 -√2/2 0 t 0 π/6 π/4 π/3 tg 0 √3/3 1 √3 ctg - √3 1 √3/3 in x = b x = (-1) n arcsin b + πn cos x = b x = ± arcos b + 2 πn tg x = b x = arctg b + πn ctg x = b x = arcctg b + πn Теорема синусов: a/sin α = b/sin β = c/sin γ = 2R Теорема косинусов: с 2 =a 2 +b 2 -2ab cos y Неопределенные интегралы ∫ x n dx = (x n +1 /n+1) + C ∫ sin x dx = – cos x + C ∫ cos x dx = sin x + C ∫ dx/sin 2 x = -ctg + C ∫ dx/cos 2 x = tg + C ∫ x r dx = x r+1 /r+1 + C Логарифмы Градус 0 30 45 60 sin 0 1/2 √2/2 √3/2 cos 1 √3/2 √2/2 1/2 tg 0 √3/3 1 √3 t π/6 π/3 2π/3 5π/6 cos √3/2 1/2 -1/2 -√3/2 sin 1/2 √3/2 √3/2 1/2 90 120 135 150 180 1 √3/2 √2/2 1/2 0 0 -1/2 -√2/2 -√3/2 -1 - -√3 -1 √3/3 0 t 7π/6 4π/3 5π/3 11π/6 cos -√3/2 -1/2 1/2 √3/2 sin -1/2 -√3/2 -√3/2 -1/2 Формулы двойного аргумента cos 2x = cos 2 x – sin 2 x = 2 cos 2 x -1 = 1 – 2 sin 2 x = 1 – tg 2 x/1 + tg 2 x sin 2x = 2 sin x · cos x = 2 tg x/ 1 + tg 2 x tg 2x = 2 tg x/ 1 – tg 2 x ctg 2x = ctg 2 x – 1/ 2 ctg x sin 3x = 3 sin x – 4 sin 3 x cos 3x = 4 cos 3 x – 3 cos x tg 3x = 3 tg x – tg 3 x / 1 – 3 tg 2 x sin s cos t = (sin (s+t) + sin (s+t))/2 sin s sin t = (cos (s-t) – cos (s+t))/2 cos s cos t = (cos (s+t) + cos (s-t))/2 Формулы дифференцирования x’ = 1 (sin x)’ = cos x (kx + m)’ = k (cos x)’ = – sin x (1/x)’ = – (1/x 2 ) ( ln x)’ = 1/x (e x )’ = e x ; (x n )’ = nx n-1 ;(log a x)’=1/x ln a Площади плоских фигур 1. Прямоугольный треугольник S = 1/2 a·b (a, b – катеты) 2. Равнобедренный треугольник S = (a/2)·√ b 2 – a 2 /4 3. Равносторонний треугольник S = (a 2 /4)·√3 (a – сторона) 4. Произвольный треугольник a,b,c – стороны, a – основание, h – высота, A,B,C – углы, лежащие против сторон; p = (a+b+c)/2 S = 1/2 a·h = 1/2 a 2 b sin C = a 2 sinB sinC/2 sin A= √p(p-a)(p-b)(p-c) a,b – стороны, α – один из углов; h – высота S = a·h = a·b·sin α cos (x + π/2) = -sin x Формулы tg и ctg tg x = sin x/ cos x; ctg x = cos x/sin x ctg (x + πk) = ctg x ctg (x ± π) = ± ctg x tg (x + π/2) = – ctg x ctg (x + π/2) = – tg x sin 2 x + cos 2 x =1 1 + tg 2 x = 1/ cos 2 x 1 + ctg 2 x = 1/ sin 2 x tg 2 (x/2) = 1 – cos x/ 1 + cos x cos 2 (x/2) = 1 + cos x/ 2 sin 2 (x/2) = 1 – cos x/ 2 P = 4 πR 2 = πD 2 V = πh 2 (R-1/3h) = πh/6(h 2 + 3r 2 ) SБОК = 2 πRh = π(r 2 + h 2 ); P= π(2r 2 + h 2 ) V = 1/6 πh 3 + 1/2 π(r 2 + h 2 )· h; 14. Шаровой сектор: V = 2/3 πR 2 h’ где h’ – высота сегмента, содержащего в секторе Формула корней квадратного уравнения ax 2 + bx + c = 0 (a≠0) Если D=0, то x = -b/2a (D = b 2 -4ac) Если D>0, то x1,2 = -b± /2a Арифметическая прогрессия a n+1 = a n + d, где n – натуральное число d – разность прогрессии; a n = a 1 + (n – 1)·d – формула n-го члена Радиус описанной окружности около многоугольника R = a/ 2 sin 180/n Радиус вписанной окружности L = 2 πR S = πR 2 Площадь конуса Тангенс угла - отношение противолежащего катета к прилещащему. Котангенс – наоборот. Читайте также:
| ||


