Интенсивные показатели заболеваемости. Длительность случая заболевания
Добавил пользователь Morpheus Обновлено: 01.02.2026
Прежде всего следует обсудить понятия "заболеваемость" и "болезненность".
Заболеваемостью ( incidence — в зарубежной литературе) принято называть число новых случаев болезни, возникших в данной группе населения в единицу времени, чаще всего — в год. Показатель заболеваемости выражается числом таких случаев на 100, 1000, 10 000 или на 100 000 населения.
Болезненность (или распространенность, prevalence — в зарубежной литературе) — это число больных с изучаемым заболеванием, которое имеется в определенном населении в данное время. Как и показатель заболеваемости, показатель болезненности рассчитывается на 100, 1000, 10 000 или 100 000 населения.
Поскольку число имеющихся среди населения больных гораздо больше, чем число вновь заболевших (во всяком случае с психическими заболеваниями), показатель распространенности чаще всего рассчитывается на 1000, а показатель заболеваемости — на 100 000 населения.
При расчете показателя болезненности, как уже говорилось, речь идет о числе больных среди населения. В последние годы предпринимаются попытки уточнить понятие "больной": ведь у одних психическое расстройство может наблюдаться сейчас, у других — в прошлом. Поэтому в современной литературе различают распространенность в момент обследования ( point prevalence ), т.е. показатель, отражающий число лиц, имеющих изучаемое психическое расстройство в данное время; годичную распространенность ( year prevalence ) — показатель, отражающий число лиц, имевших данное расстройство в любой период продолжительностью год, предшествовавшего моменту обследования; распространенность в течение жизни ( life prevalence ) 1 — показатель, отражающий число лиц, имевших отмечаемое расстройство когда-либо в жизни.
Для того чтобы проиллюстрировать различие этих показателей, воспользуемся данными В.П.Морозовой (1983), которая подробно исследовала распространенность психозов, развивающихся в виде монополярных депрессивных расстройств. Материал исследования составляли соответствующие наблюдения в 4 районных психоневрологических диспансерах (ПНД) Москвы (1703 больных). Автор обнаружила 932 случая, соответствовавших названному диагностическому критерию, что составило 1,3 на 1000 населения. Данный показатель отражает число больных, у которых депрессивное расстройство было в течение жизни (независимо от того, когда именно) — life prevalence . Если нужно установить, у какого числа больных последняя депрессия отмечалась в течение последнего года ( year prevalence ), показатель составит 1,03 на 1000, т.е. уменьшится почти на 1/4. Наконец, если желательно знать point preval ence (в данном случае — число больных, состояние которых определялось депрессией в момент осмотра), то показатель составит только 0,36 на 1000.
Существует обстоятельство, которое необходимо принимать во внимание, работая с показателями распространенности и заболеваемости. Если распространенность шизофрении в одном городе составляет 10 на 1000 населения, а в другом — 3 на 1000, то это отнюдь не означает, что в последнем люди реже болеют шизофренией; это может означать и то, что во втором случае психиатрическая служба выявляет меньше больных. Возможно, что психиатры в этих городах придерживаются разных диагностических критериев. Последняя трудность преодолевается с помощью стандартизованных инструментов диагностики, сводящих к минимуму влияние личных диагностических позиций исследователя. В любом случае обозначение критериев диагностики (как и всех других критериев отбора случаев, вошедших в исследование) является обязательным методическим требованием, которое следует учитывать при эпидемиологическом исследовании.
Известно, что разные психиатрические службы выявляют разное число больных. Это объективный и при современном уровне знаний непреодолимый факт, с которым приходится считаться. Сколько-то больных всегда остаются не выявленными и, по-видимому, не существует метода, который помог бы их всех выявить. Было много попыток выяснить показатель "истинной", "полной", "исчерпанной" болезненности. Успех всех этих попыток относителен. В большинстве эпидемиологических работ, говоря о распространенности болезни, авторы имеют в виду число больных, обратившихся за помощью. Существуют работы, авторы которых опираются на данные, полученные при поголовных осмотрах выборочных групп населения; такие показатели обычно бывают большими. Есть работы, отражающие попытки теоретически вычислить показатель распространенности эндогенных психозов (видимо, это единственный способ получить представление об их "истинной" распространенности).
Эпидемиолог очень часто сталкивается с понятиями "риск" и "вероятность". Они очень близки и в большинстве случаев означают почти одно и то же. "Вероятность", однако, — понятие более общее. Это количественное выражение меры оправданности ожидания какого-либо события. Как известно, бывают события, ожидание которых абсолютно оправдано (их вероятность принято обозначать единицей), и события, ожидание которых абсолютно не оправдано (их вероятность обозначают нулем). Подавляющее число ожиданий в большей или меньшей степени оправдано. Вероятность того, что ожидаемое событие произойдет, в этих случаях выражается числом, лежащим между нулем и единицей (для равновероятных ожиданий вероятность составляет 0,5). Сумма вероятностей всех возможных вариантов ожидаемого события всегда составляет единицу.
Оценка вероятности того или иного события составляет значительную часть работы эпидемиолога. Базой для этого служит частота изучаемого явления в репрезентативной выборке. Это дает представление о величине риска (или просто о риске) возникновения болезни, развития нового приступа и т.д.
Особого внимания заслуживает термин " популяция ". Он, пожалуй, наиболее часто встречается в статьях по эпидемиологии психических заболеваний. Говорят просто о популяции, о популяции больных, о популяции больных с определенным расстройством, о популяционных исследованиях и популяционных закономерностях.
Популяция — это совокупность особей одного вида, длительно занимающая определенное пространство и воспроизводящая себя в течение большого числа поколений. Из этого определения следует, что вполне позволительно говорить о популяционных исследованиях или о популяционных закономерностях, если речь идет о том или другом применительно к населению данной территории. Но, очевидно, не следует говорить о "популяции больных".
Выборка . На этом понятии необходимо остановиться более подробно. В идеале в исследование должны были бы быть включены все случаи данного заболевания. Подобная группа называется генеральной совокупностью. Поскольку исследование генеральной совокупности или невозможно, или требует неоправданно большого труда, лучше обойтись более ограниченным материалом, который и называют выборкой. Очевидно, что она должна быть такой, чтобы полученные при ее изучении результаты можно было распространить на любую другую группу аналогичных случаев (входящих в генеральную совокупность). Это, возможно, если в выборку попали все разновидности случаев, имеющихся в генеральной совокупности, причем в таком же количественном соотношении. Такая выборка представляет генеральную совокупность и поэтому называется репрезентативной (от англ. rep resent — представлять).
Поскольку исследователь имеет дело с выборкой, а не с генеральной совокупностью (в сущности так обстоит дело и при невыборочных обследованиях), результаты не могут быть абсолютно точными. Иными словами, в каждом результате эпидемиологического исследования имеется статистическая ошибка. Величина ошибки находится в обратных отношениях с численностью выборки: чем выборка больше, тем ошибка меньше. От величины ошибки зависит приемлемость результатов: если возможные колебания показателя невелики, то результаты, очевидно, приемлемы; если они слишком большие, то ценность результата чаще бывает сомнительной.
Статистическая ошибка связана с величиной, которая называется уровнем надежности результатов исследования. Если работа выполнена грамотно, то другие исследователи, повторяя ее на других выборках, скорее всего получат примерно такие же показатели. Но в принципе может встретиться выборка, в которой результат будет резко отличаться от остальных (на гораздо большую величину, чем статистическая ошибка). Необходимо знать, сколько может быть таких исключений. Показатель, характеризующий последнее, называется уровнем надежности (или просто надежностью) полученных результатов. Уровень надежности задается исследователем при планировании работы. Каков он должен быть, зависит от той области, в которой осуществляется исследование. В биологии и медицине принято считать, что достаточным является уровень надежности, равный 95 %, или 0,95 (именно это означает часто встречающаяся в статьях статистическая формула р<0,05), т.е. из каждых 100 выборок резко отличающийся результат может получиться не более чем в 5. Большая надежность требует значительного увеличения материала и затрат труда, которые в медицине чаще всего не оправданы (хотя и в медицинском исследовании надежность, равная 95 %, может быть недостаточной).
Поскольку характеристики генеральной совокупности заранее неизвестны, то нужно каким-то приемом добиться, чтобы в выборку попали те больные и в том соотношении, которое нужно, а также следует правильно определить ее численность. Первое достигается с помощью случайного отбора, т.е. выбор наблюдений организуют так, чтобы все случаи имели равные шансы попасть в создаваемую группу. Конкретных способов добиться этого достаточно много. Можно, например, составить картотеку из всех проживающих на данной территории больных, перетасовать ее и взять нужное число карточек. Существуют "алфавитные" способы, базирующиеся на том, что известна частота фамилий, начинающихся на ту или иную букву. В группу отбирают нужное число лиц с соответствующими фамилиями. Этот способ применяют при выборке из очень больших совокупностей (например, из населения региона). Наилучшим для выбора наблюдений из сравнительно небольших совокупностей (например, пациенты больницы или диспансера) представляется использование случайных чисел. По произвольному и независимому от изучаемых характеристик принципу составляют список всех больных (например, по алфавиту), нумеруют их фамилии по порядку, и далее с помощью компьютера (или из таблиц случайных чисел, имеющихся в большинстве руководств по статистике) получают столько случайных чисел, сколько больных предполагается включить в выборку; потом отбирают соответствующие номера из списка.
Определение численности выборки — отдельная и достаточно трудная задача. Именно из-за ее трудности многие предпочитают брать заведомо очень большие выборки, чтобы обеспечить репрезентативность наверняка. Крайний пример — невыборочное обследование, когда в список включают всех имеющихся больных, хотя 50 % или даже 25 % больных тоже может быть достаточно. Если генеральная сово купность невелика (например, выборы должны касаться только пациентов данного отделения), то такой способ может оказаться наиболее приемлемым. Но если выводы должны быть распространены на город или регион, то затраты труда на обследование тысяч больных могут быть невозможными или неоправданными. Целесообразнее затратить некоторое время на определение разумной численности выборки.
Для того чтобы объяснить, как это делается, придется вернуться к понятиям статистической ошибки и уровня надежности результатов.
Ошибка относительных показателей (выраженных в процентах) рассчитывается по формуле:
Из формулы видно, что величина ошибки находится в обратной зависимости от численности выборки. С одной стороны, чем меньше численность выборки, тем ошибка больше, с другой — чем больше показатель р (т.е. чем больше доля случаев с изучаемой особенностью), тем больше выборка. Иными словами, при планировании работы необходимо, исходя из некоторой рабочей гипотезы, представлять себе обе величины. Если о них нет никакого представления, приходится провести небольшое пробное обследование, чтобы установить их порядок (доли процента, целые проценты, десятки процентов).
Интенсивные показатели
В эпидемиологии при изучении заболеваемости используют несколько разновидностей интенсивных показателей, объединяемых общими терминами: «показатели заболеваемости» или «показатели частоты заболеваний» «меры частоты заболеваний», «коэффициенты заболеваемости».
Общая формула расчета интенсивных показателей (исключая показатель человек-время):
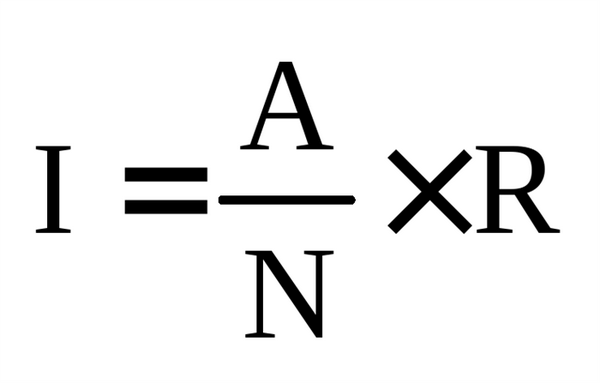
где:
I - одна из разновидностей интенсивного показателя;
A (или Абс.)- абсолютное число случаев какой-либо болезни в определенной группе населения (группе риска) за данный отрезок времени, на данной территории;
N - численность той же группы населения (группы риска), среди которого выявлены "А" случаев указанной болезни за тот же отрезок времени, на той же территории;
R - размерность показателя, которая может выражаться любым числом 10n:
-в долях единицы (редко);
-в процентах, т.е. на 100 человек - 0/0;
-в промилле - на 1000 человек - 0/00;
-в продецимилле - на 10000 человек - 0/000;
-в просантимилле - на 100000 человек - 0/0000.
В дальнейшем в тексте, таблицах и графиках мы будем использовать знаки размерности а не их словесное выражение. Например, «заболеваемость на 100000 население» будет обозначаться просто как 0 /0000
Как следует из формулы, показатель частоты отличается от абсолютного числа заболеваний, прежде всего, тем, что он рассчитывается относительно численности группы риска (группы населения).
Нередко показатели заболеваемости всего населения данной территории называют "общими, грубыми", а показатели отдельных групп - " групповыми, специфическими, частными". Следует особо подчеркнуть, что путем сложения всех групповых интенсивных показателей нельзя (в большинстве случаев) получить показатель заболеваемости всего населения, так как каждый групповой показатель рассчитан для разной численности населения. Чтобы оценить заболеваемость всего населения необходимо общую сумму больных разделить на численность этого населения.
Как уже указывалось, размерность интенсивных показателей может быть любой, при этом показатели заболеваемости населения городов, областей, стран чаще всего выражают в просантимилле ( 0 /0000, т.е. на 100000 населения). Для оценки заболеваемости небольших по численности групп риска применяют остальные размерности вплоть до процентов. Однако при сравнении нескольких показателей необходимо использовать их одинаковую размерность.
При необходимости можно легко изменить размерность показателя, для чего следует переместить запятую влево или вправо от первоначального положения.
Например, показатель 1532,1 0 /0000при переводе в другие размерности будет выглядеть как 153,2 0 /000или 15,3 0 /00, или 1,5 0 /0.
Если важно "заострить" внимание на величинах риска заболеть, какой-либо болезнью, следует выбрать наиболее воспринимаемую (наглядную) размерность показателя.
Так, в приведенном выше примере гораздо легче воспринимается риск заболеть, выраженный в процентах (т.е. 1,5 случая на 100 человек), чем та же информация в просантимилле (т.е. 1532,1 случая на 100000 человек).
Так же трудно воспринимается, например, риск заболеть обозначенный как 0,02 0 /0, т.е. 0,02 случая на 100 человек. Такой риск следует выразить в продецимилле, т.е. 2,0 0 /000(2 случая на 10000), или в показателях большей размерности.
Любые величины заболеваемости, абсолютные или относительные, это величины именованные, т.е. обязанные иметь необходимые имена - названия, без которых использование величин теряет всякий смысл.
Так, например, информация о том, что “Заболеваемость составила 1276,3 0 /0000,” не имеет никакого эпидемиологического смысла. Если даже уточнить, что “Заболеваемость суммой ОКИ (острые кишечные инфекции) составила 1276,3 0 /0000”, то и это не изменит предыдущего отношения к данным. Даже более подробная информация - «Заболеваемость суммой ОКИ в г. Москве составила 1276,3 0 /0000» и даже «Заболеваемость суммой ОКИ в г. Москве в 2002 г. составила 1276,3 0 /0000» не позволяет однозначно понять эти данные. Это связано с тем, что в первом случае отсутствует обозначение группы риска и времени, а во втором, хотя и указано время, но вновь отсутствует название группы риска. Абсолютно точная информация, соответствующая этому показателю выглядит следующим образом: «Заболеваемость суммой ОКИ детей до 14 лет в Москве в 2002 году составила 1276,3 0 /0000»
Из сказанного следует, что абсолютные или относительные цифры заболеваемости обязательно должны сочетаться с названием болезни, временем, местом выявления (регистрации) больных, названием группы риска (все население, или отдельные его группы) и размерностью (если цифры относятся к показателям).
Если обозначается заболеваемость всего населения, обычно слово всего опускается, например, «заболеваемость населения г. Н» означает что речь идет о заболеваемости всего населения г. Н, а не какой-либо его группы
К сожалению, даже в зарубежной литературе (а именно западные эпидемиологи разработали большинство показателей) названия одних и тех же показателей существенно различаются. Ещё большая путаница отмечается в русских названиях одних и тех же показателей. Особенно это относится к показателю prevalence rate, который переводится в разных изданиях и как «показатель распространённости», и как «показатель болезненности», и как «показатель пораженности». Поэтому, читая эпидемиологическую литературу следует доверять не названию показателя, а только формуле его расчёта.
В эпидемиологических исследованиях используют следующие интенсивные показатели:
показатель инцидентности(заболеваемости) -incidencerateилиcumulativeincidencerateилиR;
показатель превалентности- prevalence rate (две разновидности);
показатель инцидентности человек-время- -person-timeincidencerate, или показатель плотности инцидентностиincidencedensity
показатель очаговости- attack rate (две разновидности).
В аналитических исследованияхпри расчетах частоты заболеваний, или частоты клинических исходов болезни среди лиц опытной и контрольной группы,показатель инцидентности или показатель человек-время в сравниваемых группах часто называют показателями абсолютного риска заболеть (R) в опытной и контрольной группах,но способы их расчета при этом не изменяются.
В последнее время, существует разумная тенденция обозначать некоторые показатели в русском звучании английского названия показателя (а не в его переводе). Так, показатель incidence rate лучше именовать показателем инцидентности, prevalence rate - показателем превалентности.
Эпидемиологический смысл большинства интенсивных показателей заболеваемости выражается в том, что они отражают:
частоту (frequency) случаев (вновь выявленных или всех случаев) данной болезни в какой- либо группе населения (группе риска) за данный период (момент) времени на данной территории;
долю (fraction) заболевших (больных) данной болезнью в той же группе за то же время на той же территории;
средний, для каждого жителя,риск (risk)заболеть, или быть больным данной болезнью в той же группе, за то же время, на той же территории. Среднийрискможно выразить так же, как среднюю для каждого жителявероятностьзаболеть, или быть больным данной болезнью в той же группе, за то же время, на той же территории.
Нередко у читателя возникают сомнения в том, что интенсивные показатели могут отражать одновременно и частоту и долю заболевших. Однако необходимо учитывать, что все интенсивные показатели заболеваемости являются, так называемыми,альтернативными показателями, т.е. показателями, расчёт которых основан на противопоставлении двух групп населения - больных и здоровых (т.е. остальной части населения). Поэтомупоказатели заболеваемости (исключение составляет person-time incidence rate) отражают одновременно и частоту случаев указанной болезни в группе риска за данный период (момент) времени и долю заболевших (больных) данной болезнью в той же группе за то же время.
Например, показатель инцидентности (заболеваемости) гриппом (всего) населения г. Москвы в 2002 году составил 1075,0 0 /0000. Это означает, что частота заболеваний гриппом всего населения г. Москвы в 2002 г. составила 1075,0 человека на каждые 100000 населения. Кроме того, та же цифра, выраженная в процентах, указывает, что доля заболевших гриппом среди всего населения г. Москвы в 2002 году составила 1,07 0 /0. Этой же величиной, естественно, одновременно отражается и средний риск заболеть гриппом для любого жителя Москвы в 2002 г.
Все интенсивные показатели являются кумулятивным, т.е. представляющими число случаев данной болезни (вновь выявленных или всех существующих),накопленных к концу определенного периода (момента).
В последнее время, особенно при описании результатов аналитических исследований, вместо термина вероятность заболеть используется термин шансы заболеть. Шансы (odds)- в общем случае, это отношение вероятности того, что событие произойдет, к вероятности того, что событие не произойдет. При расчетах шансоввероятностьчаще всего выражаютв долях единицы.
Если вероятность выражается в размерности большей единицы, например в %, или 0 /00, то единица в знаменателе формулы заменяется соответственно на 100 или 1000. Шансы и вероятности содержат одну и ту же информацию, но по-разному выражают ее.
Например, распространенность артериальной гипертонии (АГ) в Москве в период 1979 - 1981 г.г. среди женщин 60-69 лет составляла 57,6%, что соответствует средней вероятности быть больным (АГ) для этой категории населения, на этой территории, в данный период времени.Шансы быть больной при тех же условиях составят 57,6/(100-57,6)= 1,4. Шансы, выражают как отношение шансов к какой либо цифре, в данном примере, как1,4 :1, т.е. шансы женщин в возрасте 60-69 лет в Москве в период 1979 1981 г.г. быть больным АГ составляли1.4 к 1.
Зная величину шансов при необходимости легко рассчитать вероятность:
Так, по данным предыдущего примера: вероятность = 1,4/(1+1,4)=0,576 или 57,6%.
Для некоторых расчетов шансы удобнее использовать, чем вероятности. Для всех инфекционных болезней в обычной эпидемической обстановке, вероятность заболеть каждого жителя, а, следовательно, и его шансы заболеть незначительны.
Например, показатель заболеваемости гриппом и ОРВИ (самый большой из всех инфекций) населения Москвы в 2002 году составил 31666,6 0 /0000. Эта цифра соответствует средней вероятности заболеть каждого жителя Москвы в 2002 году. Шансы каждого жителя в этом случае оцениваются как 31666,6/(100000-31666,6)= 0,46, или0,46 к 1, или 4,6 к 10.
1. Интенсивные показатели.
Интенсивные показатели используются в тех случаях, когда необходимо оценить распространенность изучаемого явления в среде, с которой оно связано. Иными словами относительные величины частоты отвечают на вопрос, как часто встречается изучаемое явление в той среде, в которой оно происходит. Относительные величины частоты можно рассчитывать на различные основания - на 100, 1000, 10 000 и т. д.
Методика вычисления интенсивных показателей проводится на основании пропорции:
Относительная величина частоты
Абсолютная величина явления х 100 (1000, 10 000 и т.д.)
Абсолютная величина среды
Типичными интенсивными показателями являются показатели рождаемости, смертности, заболеваемости в тех или иных группах людей и в определенное время.
2.Экстенсивные показатели.
Относительные величины распределения используются в тех случаях, когда необходимо количественно характеризовать распределение целого на составляющие его части. Иными словами, относительные величины распределения отвечают на вопрос о том, какую долю (%) среди всего явления в целом, принимаемого за 100%, занимает его любая составная часть.
Методика определения относительных величин распределения проводится на основе элементарной пропорции:
Абсолютная величина изучаемого явления - 100%
Величина любой составной части явления - Х%.
Отсюда относительная величина распределения Х:
Абсолютная величина любой составной части явления х 100
Абсолютная величина всего изучаемого явления
Распределение инфекционных заболеваний рабочих предприятия по видам болезней
Диагноз заболевания
Абсолютное количество случаев
Относительные величины распределения (структура) в %
Прочие инфекционные б-ни
Экстенсивный показатель характеризует долю какой-то части изучаемого явления в общей совокупности и ничего не говорит о величине этой части.
Экстенсивными показателями можно характеризовать распределение родившихся по полу, росту, весу; распределение умерших по возрасту, полу и причинам смерти; распределение больных по нозологическим формам, по срокам госпитализации; состав населения по полу и возрасту. В некоторых случаях возможно применение только экстенсивных показателей, например, формула элементов белой крови.
Характерной чертой экстенсивных показателей является их взаимосвязанность, вызывающая автоматизм сдвигов, так как их сумма всегда составляет 100%. Так, при изучении структуры заболеваемости, доля какого-нибудь отдельного заболевания может возрасти:
а) при подлинном его росте, т.е. при увеличении абсолютных величин и интенсивного показателя;
б) при одном и том же уровне - если число других заболеваний в этот период снизилось;
в) при снижении уровня данного заболевания, если уменьшение числа других заболеваний происходило более быстрым темпом.
Делать выводы об интенсивности явления в разных совокупностях на основании их долей нельзя.
Интенсивные показатели заболеваемости. Длительность случая заболевания
В процессе эпидемиологического анализа приходится постоянно оперировать также такими статистическими понятиями, как интенсивные и экстенсивные показатели, средние величины и т.д.
Экстенсивный показатель — это доля определенного варианта того признака, который в той или другой разновидности встречается во всех изучаемых случаях. Обычно он выражается в процентах. Экстенсивные показатели взаимозависимы: если в изучаемой группе психически больных (то, что все составляющие группу лица, психически больные — это признак) случаи шизофрении (диагноз — вариант этого признака) составляют 60 %, то на прочие заболевания придется 40 %.
Интенсивный показатель — это мера частоты определенного признака среди тех случаев, в которых этот признак может быть, а может и не быть. Если мы говорим, что распространенность шизофрении среди населения составляет 1 на 1000, то это интенсивный показатель. Он не зависит от других интенсивных показателей: среди населения может быть сколько угодно больных с другими заболеваниями и здоровых, а показатель распространенности шизофрении при этом не изменится.
Использование экстенсивных и интенсивных показателей зависит от задачи исследования. Если нужно решить, как распределить имеющийся коечный фонд для лечения пациентов разного возраста, то нужны экстенсивные показатели, характеризующие возраст больных: сколько процентов среди них составляют дети, лица среднего и лица пожилого возраста. Если же нас интересует, у кого чаще отмечаются психические расстройства — у детей, людей старшего возраста или у стариков, то экстенсивные показатели ничего не дадут: может случиться, что процент пожилых среди пациентов будет очень высоким, потому что в городе значительную часть населения составляют пожилые люди. Для решения этой задачи необходимы интенсивные показатели: сколько приходится больных на 1000 детского населения, на 1000 пожилого населения и на 1000 населения среднего возраста. Тогда сравнение будет адекватным.
Средняя величина (точнее среднее арифметическое) — одно из самых частых понятий, используемых в эпидемиологических исследованиях. Говорят о средней длительности пребывания больного на койке, среднем числе посещений диспансера в день, средней длительности ремиссий и о множестве других средних величин. Не останавливаясь на вычислении среднего арифметического, рассмотрим вопрос о содержательном значении средней величины.
Если утверждается, что, например, средний рост мужчины составляет 175 см, то смысл этого утверждения очень глубок. Существует фундаментальная причина, определяющая именно эту величину: рост — генетически обусловленный признак (именно поэтому мужчины в среднем выше женщин).
Врач сталкивается с множеством подобных явлений. Это размеры и масса живых существ, длительность пребывания больного на койке, количество препарата, нужное для лечения определенного расстройства, и во всех этих случаях средняя величина имеет совершенно четкий смысл: она указывает, что причина явления определяет именно эту характеризующую его величину, а все отклонения от нее определяются влиянием случайностей.
Статистическое распределение количественных характеристик отдельных случаев, относящихся к подобному явлению, всегда бывает так называемым гауссовским, или нормальным (рис. 25). Если желательно использовать для характеристики каких-то данных их среднюю величину, следует проверить, соответствует ли распределение этих данных нормальному; если да, то применение средней величины оправдано, она имеет смысл: именно средняя величина определяется основной причиной изучаемого явления. Однако часто при такой проверке обнаруживается, что данные распределяются иначе. В частности, длительность многих психопатологических состояний имеет экспоненциальное (а не нормальное) распределение, которое свидетельствует о том, что количественная характеристика каждого отдельного наблюдения случайна. Средняя величина в таких случаях не имеет содержания. Именно поэтому в ядерной физике не употребляют понятие "среднее время распада ядер" радиоактивного вещества, а говорят о "периоде полураспада", т.е. о времени, за которое распадается половина всех имеющихся ядер. Подобно этому не следует характеризовать средними величинами и длительность психопатологических синдромов.
При эпидемиологических исследованиях часто сравнивают две выборки (или более). При этом может возникнуть проблема их несопоставимости (например, выборки очень различаются по возрастной структуре, что мешает решить поставленную задачу). В таких случаях помогает метод стандартизации данных, описанный, например, Н.А.Вигдорчиком (1945). Смысл этого метода заключается в том, что искусственно устраняется различие между выборками по всем факторам, кроме изучаемого.
С проблемой проверки достоверности статистических различий эпидемиолог сталкивается всякий раз, когда сравнивает два показателя. Если в каждой из срав ниваемых групп не меньше 20 наблюдений, то на этот вопрос отвечает критерий Стьюдента (Т), вычисляемый по известной формуле:
где p 1 и р2 — сравниваемые показатели, n 1и n2 — численность подвыборок.
Достоверным считается то различие, при котором разность между показателями в определенное число раз больше, чем сумма их ошибок. Это число (Т) определяется тем уровнем надежности, который принят в данном исследовании. При таком условии число Т (критерий Стьюдента) должно быть больше 2. Если это так, то различие считается достоверным: можно быть уверенным, что по крайней мере в 95 из 100 любых аналогичных выборок различие окажется примерно таким же (плюс-минус ошибка).
Если сравниваемые группы маленькие (содержат менее 20 наблюдений), то для проверки достоверности различий между ними метод Стьюдента непригоден. Поэтому обычно стараются избегать слишком маленьких групп. Однако это не всегда возможно, и тогда приходится применять так называемый точный метод Фишера. С его помощью вычисляется не условный коэффициент (как при методе Стьюдента), а величина вероятности, что полученный результат случаен. Если эта вероятность меньше 0,025, то различие признается достоверным.
Вычисление критерия Стьюдента — вполне выполнимая задача, рассчитать же вероятность случайного результата по методу Фишера труднее. Помогают специальные таблицы, в которых, зная численность изучаемых групп и различия между ними, можно посмотреть, достоверны ли они [Генес B . C ., 1967].
Различия, которые при проверке оказываются статистически недостоверными, могут тем не менее иметь большое значение. Особенно часто это случается, когда сравнивается ряд показателей, характеризующих, например, динамику какого-либо процесса. Важным может оказаться не определение достоверности различий соседних показателей, а закономерность их изменений. Закономерные изменения всегда говорят о чем-то важном, независимо от того, достоверны ли различия между составляющими ее показателями.
Анализируя изменения показателей, постоянно приходится думать, не закономерны ли эти изменения. С распространением компьютерных технологий обработки полученных данных эта задача стала простой. Например, программный пакет " Microsoft Excel " решает ее автоматически, подбирая к экспериментальным данным линию тренда (определяя тенденцию их изменений) и указывая, насколько точно она их описывает.
Одной из главных методологических проблем при организации эпидемиологических исследований в психиатрии является идентификация больных. Последняя при эпидемиологическом обследовании отличается от обычной клинической диагностики. Массовость материала заставляет эпидемиолога опираться на стандартные диагностические критерии. Это требование вступает в очевидное противоречие со стремлением иметь как можно более добротный в клиническом отношении материал. При компромиссном решении, которое приходится принимать, неизбежно в жертву приносится либо стандартность диагностики, либо степень ее клинической фундированности. Зарубежные авторы, как правило, жертвуют последним, отдавая безусловный приоритет обеспечению сопоставимости материала разных исследователей. Поэтому они уже много лет используют формальные диагностические инструменты (опросники, шкалы, структурированные интервью и т.п.).
Клинико-эпидемиологический метод, описанный ранее и на протяжении многих лет используемый в отделе эпидемиологии Научного центра психического здоровья РАМП, характеризуется тем, что исследователи, применяя его, отдают предпочтение клинической добротности материала, а это затрудняет сравнение полученных результатов с данными зарубежных авторов. Изложенные трудности идентификации больных могут быть, по-видимому, отчасти преодолены использованием МКБ-10, поскольку эта международная диагностическая система снабжена подробной методикой постановки диагноза, обеспечивающей полную стандартность диагностики, без изменения клинического содержания диагноза.
Читайте также:
- Тромбофлебит мозговых синусов ушного происхождения. Симптомы, диагностика и прогноз синустромбоза
- Нейтрализация протонов почками. Первично активный механизм секреции ионов водорода почками
- Тактика при коме. Госпитализация при коме.
- Спорные вопросы операции по поводу толстокишечной непроходимости.
- Саркоидоз орбиты глаза: причины, диагностика, лечение
