Математическая модель вирус гриппа

Детектив: откуда взялся COVID-19 и как перемещается (ENG)

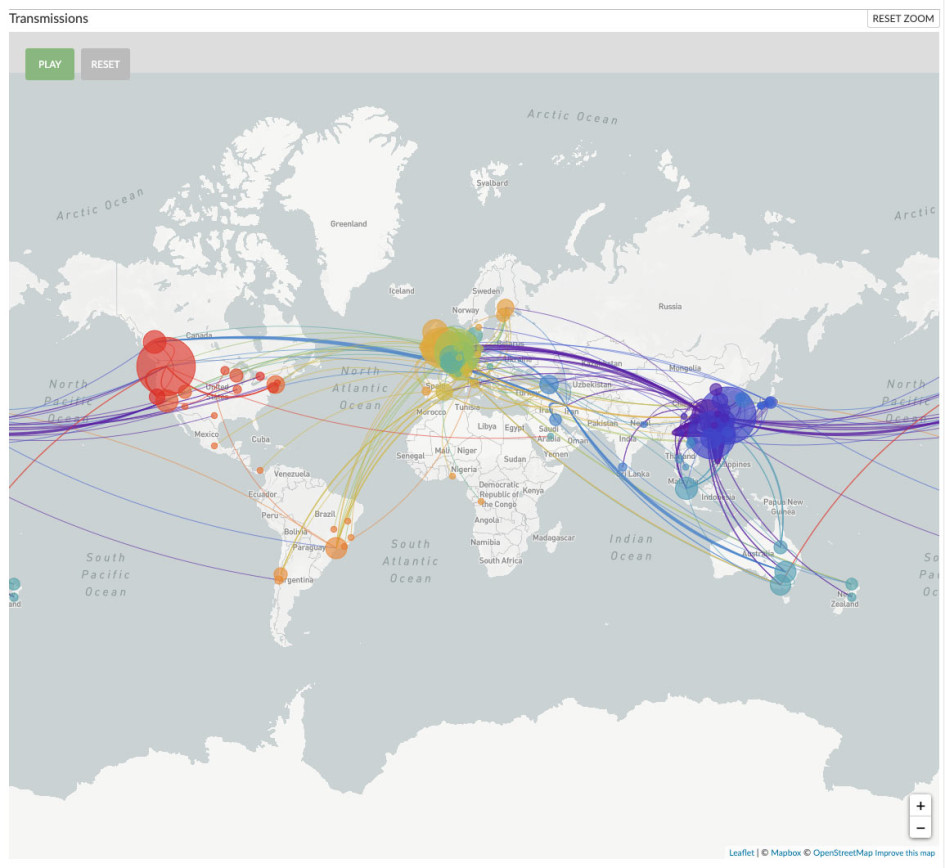
Демография имеет значение (ENG)

Поскольку летальность COVID-19 значительно увеличивается с возрастом пациента, особенности возрастных структур населения могут оказывать значительный эффект на общую смертность от пандемии коронавируса. Демограф Илья Кашницкий оценил этот эффект и отобразил на карте различия в возрастных структурах населения регионов Европы.

За основу взяли данные о летальности пандемии в Италии — первой европейской стране, где ситуация начала развиваться очень быстро, и к 17 марта было зафиксировано уже 2003 смерти. Предположив, что во всех прочих регионах Европы летальность будет такой же как мы наблюдали в Италии, а общее число инфицированных достигнет 2/3 населения (цифра, о которой упоминала в своем обращении Ангела Меркель), рассчитали долю населения с повышенным риском умереть от пандемии. Надо отметить, что эта величина не претендует на роль сколько-нибудь точного прогноза финальной летальности. Допущения при расчетах очень значительны и маловероятны в долгосрочной перспективе. Однако, суть исследования — в сравнении возрастных структур населения. Различия между ними останутся неизменными, даже если повозрастная летальность от COVID-19 окажется существенно отличной от наблюдаемых сейчас в Италии величин, важно лишь, чтобы различия между возрастными группами оставались схожими.

Проведенный анализ позволяет выявить потенциально наиболее уязвимые регионы. Наибольшие потери населения из-за пандемии вероятны в странах и регионах с наиболее возрастным населением — Италия, Германия и Испания. Самый интересный вывод: несмотря на то, что сейчас наибольшее количество зарегистрированных случаев заражения и смертей концентрируется в больших городах, куда вирус пришел раньше, при масштабном неконтролируемом распространении наиболее проблемными станут отдаленные периферийные районы с наиболее пожилым населением. Это еще одна причина, почему карантинные меры, призванные растянуть во времени пик пандемии, чрезвычайно важны, особенно в странах Европы с относительно старым населением.

Источник: Kashnitsky, I. (2020). COVID-19 in unequally ageing European regions. OSF Preprint.

Экспоненциальный рост и эпидемии (ENG, RUS)

Математик объясняет, в какой момент нужно начинать беспокоиться. Эпидемия развивается экспоненциально — это значит умножение на какую-то константу (постоянный коэффициент).

Согласно данным на начало марта число случаев каждый день превышало число случаев в предыдущий день в 1,12—1,25 раз. Изменение количества зараженных изо дня в день складывается из трех цифр: количество зараженных в определенный день (N), среднее количество человек, с которым зараженный может контактировать в определенный день (E), и вероятность каждого контакта стать новым случаем заражения (p). Соответственно, по данным на 6 марта, в среднем каждые 16 дней количество зараженных увеличивалось в 10 раз. Но просто провести восходящий тренд недостаточно: в какой момент рост кривой должен остановиться. И важную роль начинают играть переменные E и p — они должны снижаться, чтобы остановить экспоненциальный рост.

Интерактивная модель: как распространяется вирус (ENG)

У The Washington Post вышел интерактивный материал о том, как распространяются инфекции. Основная идея — показать, почему важно ограничивать контакты каждого конкретного человека с внешним миром, а вот закрывать города и страны совсем необязательно. Симуляции показывают, как изменяется кривая количества зараженных в зависимости от того, какая стратегия используется: не делать ничего; попытка закрыть город на карантин; социальная изоляция четверти населения; социальная изоляция 7/8 населения.

Мягкая изоляция выигрывает у карантина, а почти полная изоляция — статистически наиболее надежный способ остановить эпидемию. Симуляции случайные, каждое прочтение статьи даст немного разные результаты, но вывод останется прежним.

Блогер Кевин Симлер улучшил эту модель: он добавил новые вводные (например, инкубационный период и количество умерших от болезни) и параметры модели, которые можно настраивать вручную. Здесь по шагам объясняется, как распространяется вирус и какие переменные на это влияют: например, в одной из симуляций предлагается угадать, какой должна быть скорость передачи заболевания между людьми, чтобы она не успела заразить все население планеты.

Так что это не только подробное пошаговое объяснение того, как распространяется вирус, но еще и упражнение в интуиции и критическом мышлении.

Люди хотят закрытия границ (RUS)

По данным исследования Ipsos по восприятию коронавируса, большинство людей считают, что границы их стран должны быть закрыты до тех пор, пока не будет локализована эпидемия. В опросе приняли участие 12 000 человек из 12 стран. Жители Азиатско-Тихоокеанского региона активнее всех поддерживают идею закрытия границ — во главе с Индией (79%) и Вьетнамом (78%) — что неудивительно, учитывая локацию, в которой болезнь была обнаружена впервые. В Италии 76% также согласны с этой радикальной мерой. Далее следуют Китай (73%) и Россия (70%).

Растет количество человек, которые верят в вероятность заражения людей из их ближнего окружения: их уже больше половины респондентов во Вьетнаме (67%), Великобритании (57%), половина в Индии, Австралии и Японии (51%).

Что ученые знают о 2019-nCoV (RUS)

Сейчас идет разработка лекарств, которые ингибируют заражение на разных стадиях цикла репликации вируса, и вакцин от SARS-CoV/MERS-CoV. Однако пока специфических препаратов от коронавирусов нет, и лечение заключается в поддерживающей терапии, назначенной по состоянию пациента. Источник на 11 марта 2020 года.

Материал обновляется.

Как математика помогает бороться с эпидемиями

Эпидемии издавна угрожали человечеству, и только в ХХ веке были разработаны эффективные средства борьбы с инфекциями. К числу этих средств принадлежат и системы дифференциальных уравнений — математика помогает моделировать распространение эпидемий и помогает понять, как следует с ними бороться. Это наш третий материал о самых интересных дифференциальных уравнениях и о том, где и как они применяются (предыдущие материалы можно прочитать здесь и здесь). Если вы читаете нас с телефона, переключайте страницу на десктопную версию, так вы сможете увидеть интерактивный график целиком.

В XXI веке мир уже успел столкнуться с эпидемией птичьего гриппа в Юго-Восточной Азии (в 2013 году) и вспышкой заболеваний лихорадкой Эбола в Африке (2015). Но в истории человечества бывали и куда более масштабные эпидемии.

В 551-580 годах нашей эры в Восточной Римской империи разразилась первая задокументированная пандемия чумы, получившей название Юстиниановой, в результате которой погибло около 100 миллионов человек (по другим данным, жертв могло быть значительно меньше). Спустя еще 800 лет в Евразию и Северную Африку пришла Черная смерть — пандемия чумы, сразившая от трети до половины тогдашнего населения этих регионов.

В результате Первой мировой войны, вызвавшей перемещение большого количества людей, в 1918 году распространился испанский грипп, охвативший более 500 миллионов человек и погубивший каждого десятого заболевшего. Эта пандемия стала самой масштабной за всю историю человеческой цивилизации, коснувшись до 30 процентов населения Земли.

В медицинской классификации эпидемией называют прогрессирующее распространение инфекционного заболевания на уровне выше среднего на данной территории. В случае распространения эпидемии на большие территории или территории многих стран говорят о пандемии.

Для эпидемии среди животных применяется термин эпизоотия, а среди растений — эпифития. Этим явлениям ученые также уделяют большое внимание, поскольку они, в свою очередь, помогают понять механизм распространения инфекций.

Изучение механизмов развития и распространения эпидемий является важным способом борьбы с заболеваниями наряду с поиском новых лекарств, вакцинацией и профилактическими мерами. На помощь медикам пришли математики — для этого им пришлось объединить дифференциальные уравнения и теорию вероятности.

Первую попытку использовать математический аппарат для исследования механизмов распространения заболеваний предпринял Даниил Бернулли, ранее открывший первые законы гидродинамики. Следующий шаг сделал Уильям Фарр, применивший в 1840 году нормальное распределение к анализу смертности от оспы.

В рамках этой модели с помощью систем дифференциальных уравнений (при условии непрерывности времени и большой популяции) или разностных уравнений (при дискретном времени и ограниченной популяции) описывается динамика распространения заболевания.

SIR–модель получила заслуженную популярность в силу простоты построения и использования. Ее применение позволяет точно моделировать эпидемии гриппа и других заболеваний в больших городах, вводить новые параметры и анализировать разные сценарии.

Система уравнений SIR:

• S(t) — численность восприимчивых индивидов в момент времени t;
• I(t) — численность инфицированных индивидов в момент времени t;
• R(t) — численность переболевших индивидов в момент времени t;
• β — коэффициент интенсивности контактов индивидов с последующим инфицированием;
• γ — коэффициент интенсивности выздоровления инфицированных индивидов.

Первое уравнение системы означает, что изменение числа здоровых (и при этом восприимчивых к заболеванию) индивидуумов уменьшается со временем пропорционально числу контактов с инфицированными. После контакта происходит заражение, восприимчивый переходит в состояние инфицированного.

Второе уравнение показывает, что скорость увеличения числа заразившихся растет пропорционально числу контактов здоровых и инфицированных и уменьшается по мере выздоровления последних.

Третье уравнение демонстрирует, что число выздоровевших в единицу времени пропорционально числу инфицированных. Иначе говоря, каждый заболевший через некоторое время должен поправиться.

описывает неизменность численности популяции (и не учитывает случаи смерти от заболевания).

Графики решения выглядят так (это интерактивный график, в нем можно регулировать параметры β и γ):

Здесь синяя линия — число восприимчивых индивидов, красная — инфицированных, зеленая — переболевших.

Красный график интенсивности эпидемии, показывающей количество одномоментно болеющих индивидов, определяется параметром:

В 2012 году британская компания Ndemic Creation выпустила игру “Plague Inc.”, биологический симулятор эпидемий. По сценарию игры необходимо развить одно из выбранных заболеваний настолько, чтобы оно уничтожило жизнь на Земле.

На базовых уровнях игры распространение заболевания происходит в точном соответствии с моделью SIR. Если принять, что вместо выздоровления происходит гибель организма, то зеленый график становится графиком числа умерших — каждый игрок может увидеть его при успешном прохождении уровня.

“Plague Inc.” является одной из лучших стратегий среди существующих на рынке и на протяжении многих лет пользуется популярностью у десятков миллионов поклонников.

SIR-модель перестает работать в случае необходимости учитывать неоднородность популяции (например, различную плотность населения в разных районах), разные пути передачи инфекции и факторы случайности, значимые в малых популяциях и на начальной фазе распространения заболевания.

Развитием модели SIR стали, в частности, следующие модели:

Именно по этой модели развиваются по-настоящему опасные эпидемии, поскольку длительный инкубационный период может препятствовать своевременному обнаружению заболевания. В этом случае есть риск, что заболевание охватит значительное число индивидуумов в популяции.

• μ — уровень смертности;
• α — величина, обратная среднему инкубационному периоду заболевания;
• E(t) — численность индивидов — носителей заболевания в момент времени t.

Как и в модели SIR, первое уравнение системы означает, что изменение числа здоровых (и при этом восприимчивых к заболеванию) индивидуумов уменьшается со временем пропорционально числу контактов с инфицированными. После заражения здоровый индивид переходит в состояние контактного по данному заболеванию, или носителя инфекции.

Второе уравнение вносит задержку по времени при переходе из состояния контактного в состояние инфицированного (больного). Это происходит через время, равное инкубационному периоду болезни.

Четвертое уравнение демонстрирует, что число выздоровевших в единицу времени пропорционально числу инфицированных. При этом в каждом состоянии индивидуум может погибнуть, что учитывает коэффициент μ в каждом уравнении.

Иначе говоря, в каждый момент времени каждый индивидуум с определенной вероятностью может заразиться, через некоторое время — заболеть, а затем поправиться либо погибнуть.

Численность популяции N = S + E + I + R при этом не является постоянной с течением времени.

Интенсивность эпидемии описывает базовый коэффициент воспроизведения:

Например, построим симуляцию, использовав следующие параметры:

• На площади 20 × 20 размещены 100 индивидуумов (заполнение 25 процентов);
• Индивидуумы на каждом шаге перемещаются с вероятностью 80 процентов, в случае контакта здорового индивидуума (зеленая точка) с инфицированным (красная точка) происходит заражение с вероятностью 50 процентов;
• Заражение длится 6 дней, в течение которых возможна смерть организма с вероятностью 50 процентов либо полное выздоровление с приобретением иммунитета;
• В момент начала эпидемии примем, что инфицированы 5 процентов организмов и еще 5 процентов имеют иммунитет;
• Модель дискретная, один день = один шаг модели.

С помощью моделирования мы видим, что 49 организмов из 100 погибнут в результате эпидемии длительностью в 29 дней.

Симуляция эпидемии с заданными параметрами

Epidemic Simulator позволяет моделировать результаты эпидемий при различных плотности популяции, заразности, летальности и устойчивости заболеваний.

Вместе первое и второе уравнение означают, что число здоровых и больных в сумме не меняется, а число заражений пропорционально числу контактов здоровых и больных.

Второе уравнение описывает изменение числа заболевших в единицу времени, которое пропорционально числу заражений (числу контактов здоровых и инфицированных индивидуумов) за вычетом числа выздоровлений.

График развития заболевания в соответствии с этой моделью выглядит так (график интерактивный, можно регулировать параметры β и γ):

Синяя линия — число восприимчивых индивидов, красная — инфицированных в текущий момент.

Эта модель, построенная для заболевания с инкубационным периодом и учитывающая иммунитет детей, приобретенный внутриутробно, — одна из самых сложных для анализа в силу наличия большого числа независимых параметров. Система уравнений для нее выглядит так:

Стратегии смягчения и подавления будут основными для властей разных стран в борьбе с эпидемиями коронавируса COVID-19, считают ученые Имперского колледжа Лондона. В первом случае целью ставится замедление распространения вируса, во втором — жесткое его подавление. Оба варианта неидеальны.

Какие варианты просчитывали ученые

В опубликованном на этой неделе докладе группа ученых Имперского колледжа Лондона во главе с известным эпидемиологом Нилом Фергюсоном оценила три основных сценария развития эпидемий COVID-19 для США и Великобритании. Были смоделированы отсутствие каких-либо немедицинских мер, смягчение и подавление эпидемии.

Модели строились на основании плотности населения в разных частях стран, средних размеров домохозяйств и возраста людей, входящих в них, средней численности школьных классов, групп в университете, рабочих коллективов и соседских сообществ. Учитывались различные медицинские данные — инкубационный период вируса, скорость его распространения, доли невыявленных случаев и случаев, требующих интенсивной терапии.

Авторы оперировали пятью основными принимаемыми властями мерами (см. таблицу) — от самоизоляции до ограничения социальных контактов всего населения.

Первая модель — отсутствие каких-либо социальных мер борьбы с эпидемией — просчитана для сравнения с другими. Вряд ли какие-либо страны решатся ничего не делать на фоне всемирной пандемии.

При таком варианте пик смертности будет достигнут примерно через три месяца после начала эпидемии. 81% населения будет заражен. Количество смертей составит около 510 тыс. в Великобритании и 2,2 млн в США. Потребность в интенсивной терапии на пике будет в 30 раз превышать фактически имеющиеся ресурсы.

Как работает стратегия смягчения эпидемии

Смягчение эпидемии подразумевает не полное блокирование передачи вируса, а снижение негативного воздействия на общество: более равномерное распределение заболевших по времени, уменьшение числа тяжелых больных на пике и сокращение смертности. Сценарий предполагает в итоге формирование коллективного иммунитета и естественное прекращение эпидемии. В этом сценарии ограничительные меры действуют три месяца, наиболее эффективными из них становятся изоляция больных с симптомами вируса, карантин их семей и социальное дистанцирование для людей старше 70 лет.

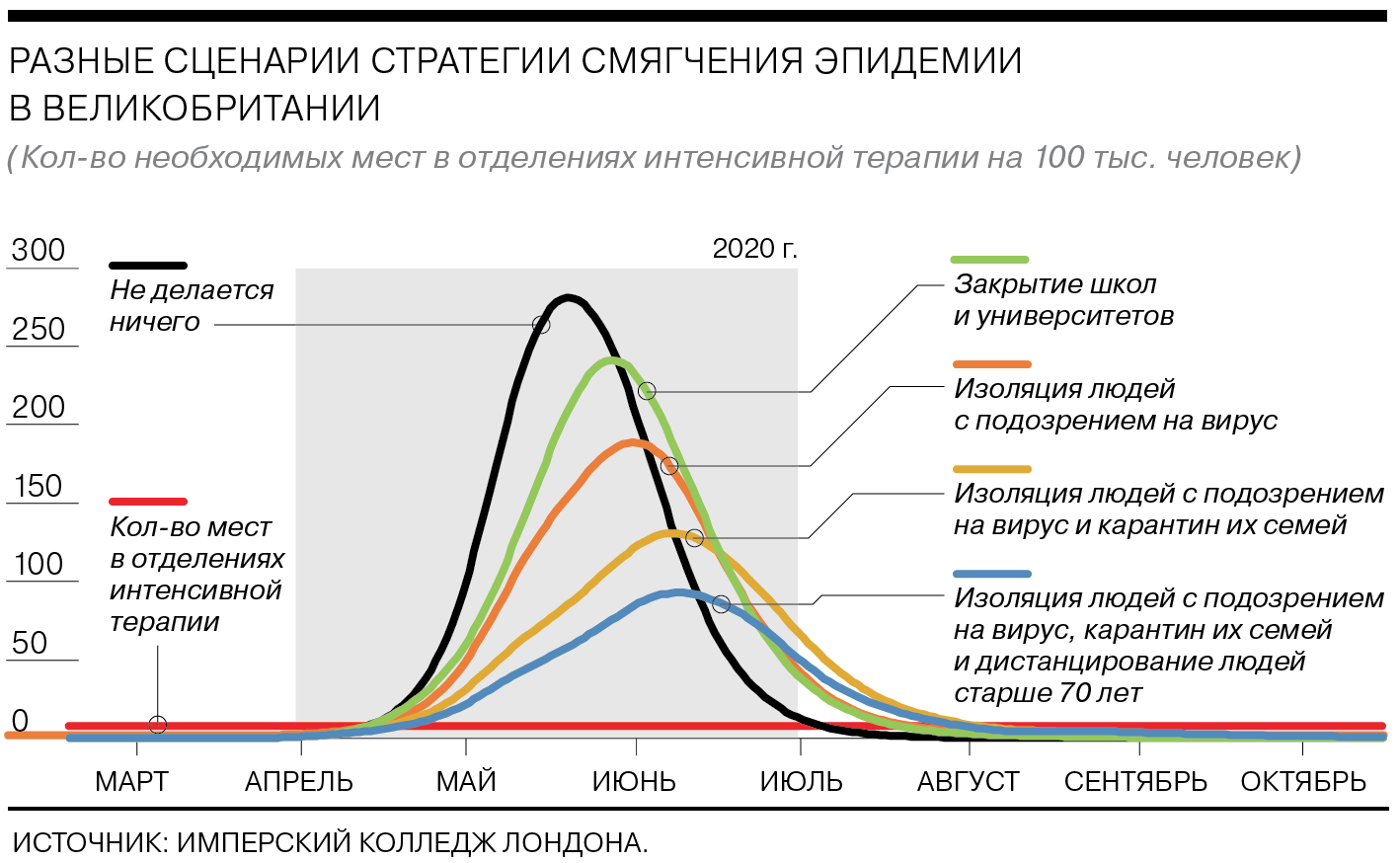
Число болеющих в пик снизится (чем более жесткие меры принимаются, тем сильнее). Но все равно нуждающихся в интенсивной терапии будет в 8 раз больше, чем мест в соответствующих отделениях.

Количество смертей от коронавируса в Великобритании при этом сценарии достигнет 250 тыс., а в США — 1,1–1,2 млн.

Как работает стратегия подавления эпидемии

Цель второй стратегии — уменьшение репродукции болезни (среднего числа людей, которых заражает один инфицированный) до уровня ниже единицы. Другими словами, нужно добиваться того, чтобы каждый заболевший передал вирус в среднем менее чем одному человеку.

В этом случае ограничения должны действовать пять месяцев. Самым эффективным вариантом будет сочетание четырех мер — изоляции людей с симптомами вируса, карантина для их семей, закрытия школ и университетов и социального дистанцирования всего населения. Лишь в таком случае нагрузка на отделения интенсивной терапии остается в рамках нормы.

По словам одного из участников исследования, профессора Азры Гани, общее число смертей в Великобритании при таких мерах может снизиться до 20 тыс., если ограничения будут строго соблюдаться.

При этом, по оценке авторов, закрытие школ и университетов будет эффективнее, чем карантин домохозяйств.

Если же жесткие меры будут отменены раньше, пик эпидемии просто будет отложен на несколько месяцев (см. график). Количество заболевших в тяжелой форме во время пика в таком случае может быть сравнимо со сценарием, при котором никакие меры не принимаются, так как коллективный иммунитет не будет сформирован.

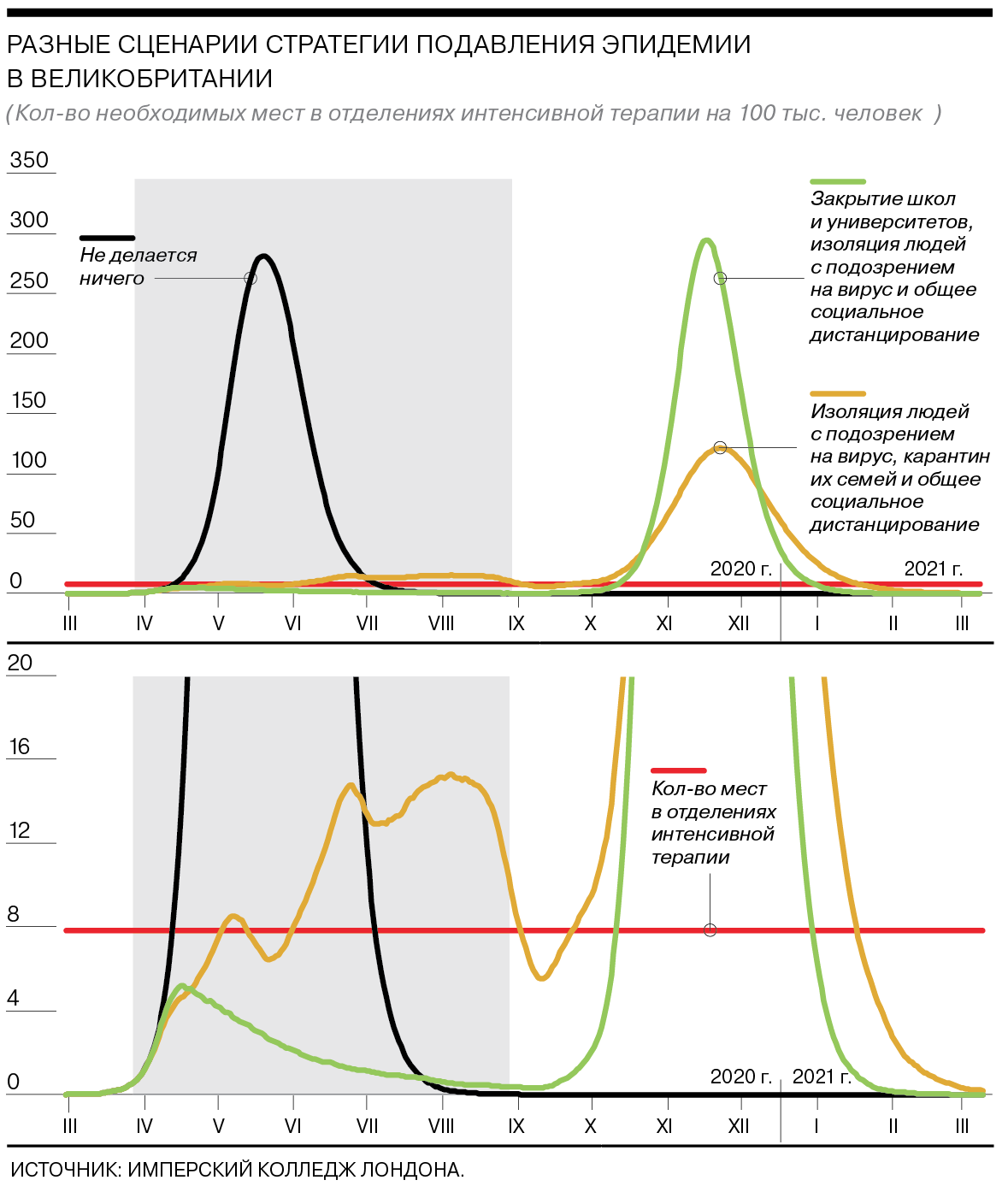
Возможен также промежуточный сценарий — адаптивный. При нем жесткие меры вводятся, когда число людей, нуждающихся в интенсивной терапии, превышает пороговое значение. Когда это число снижается, социальные ограничения отменяются. При этом изоляция людей с симптомами и карантин их семей сохраняются в течение всего времени. В этом случае эпидемия будет проходить волнообразно, а каждый последующий пик числа заболевших в тяжелой форме будет ниже предыдущего.

Реальность сложнее математических моделей

Ученые признают, что реальная эффективность принимаемых властями мер будет зависеть от реакции на них населения. Она будет отличаться от страны к стране. При этом поведение людей в условиях эпидемии будет меняться с ее течением.

Также авторы исследования отмечают, что изучали лишь то, как каждая из стратегий повлияет на распространение болезни и как отразится на системах здравоохранения. Не рассматривались этические или экономические аспекты каждой из стратегий. Авторы специально указывают, что простых политических решений быть не может.

Коронавирус-2020 в Китае и мире

Последние данные о распространении и ущербе от заболевания — в хронике “Ъ”

Сделать ее заметнее в лентах пользователей или получить ПРОМО-позицию, чтобы вашу статью прочитали тысячи человек.

• Стандартное промо
• 3 000 промо-показов 49 KР
• 5 000 промо-показов 65 KР
• 30 000 промо-показов 299 KР
• Выделить фоном 49 KР

Статистика по промо-позициям отражена в платежах.

Поделитесь вашей статьей с друзьями через социальные сети.

Получите континентальные рубли,
пригласив своих друзей на Конт.

Математическая прогнозная модель распространения вируса, основанная на:

- официальное китайское число заразившихся и потенциально заразившихся.

- общепринятая R0 2,6 (по мнению многих эпидемиологов)

- испанский грипп R0 1,8

- оружейный вирус R0> 5

Начиная с 16 января все математические схемы прогнозной модели распространения вируса, кроме той, которая была основана на Ro 2,6, не "сбылись".

То есть, R0 = 2,6, таков показатель скорости распространения вируса для Китая. Однако, учитывая, что в Китае по-прежнему разрешается проезд между всеми провинциями, кроме Тибета (наименее населенного и наиболее изолированного) и Хубэй (эпицентр пандемии), показатель R0 превысит 3 к воскресенью 2 февраля. Для развитых стран, с лучшей гигиеной, длительной историей гриппа (иммунизация) и высококачественной медицинской системой, показатель R0 (пока что) не поднимался выше 2,2.

Если развитые страны не прекратят ВСЕ путешествия до воскресенья, то ко 2 февраля R0 подскочит до 2,6. Каждый может сделать свою математику, применив R0 = 2,2 для развивающихся стран, 2,4 для азиатских стран и 2,6 для Китая, в то же время корректируя индекс вероятности распространения инфекции до 0,7-0,8.

Например, 10 х 2,2 х 0,7 для развитых стран и 10 х 2,2 х 0,8 для Юго-Восточной Азии, Южной и Центральной Америки и Африки. Для тех, кто не хочет этого делать, ниже распространение инфекции по всему миру (за исключением материковой части Китая) , начиная с сегодняшнего дня, 28 января, со всеми скорректированными цифрами:

28 января 00:00 по Гринвичу:

от 3000 до 4000 инфицированных людей на разных стадиях инкубации (от 1 до 14 дней).

Обнаружение симптомов: 37-38 случаев.

29 января, 00:00 по Гринвичу:

от 5200 до 7000 инфицированных на разных стадиях инкубации (от 1 до 14 дней).

Симптомы: 67-69 случаев.

30 января, 00:00 по Гринвичу: от 8 000 до 12 000 инфицированных людей на разных стадиях инкубации (от 1 до 14 дней).

Симптомы: 103-106 случаев.

31 января, 00:00 по Гринвичу: 12 300 - 20 100 инфицированных на разных стадиях инкубации (от 1 до 14 дней).

Симптомы: 158 - 168 случаев.

1 февраля, 00:00 по Гринвичу: 18 900 - 30 900 инфицированных на разных стадиях инкубации (от 1 до 14 дней).

Симптомы: 243 - 258

2 февраля, 00:00 по Гринвичу: 29 100 - 47 500 инфицированных людей, на разных стадиях инкубации (от 1 до 14 дней).

Симптомы: 374 - 397.

Если к этой дате не будет прекращено путешествие между всеми странами и границы не будут закрыты, эпидемия ускорится. Это цифры:

3 февраля, 00:00 по Гринвичу: 48 000 - 78 000 инфицированных , на разных этапах инкубации (от 1 до 14 дней).

Симптомы: 617 - 655

4 февраля, 00:00 по Гринвичу: 79 200 - 128 700 инфицированных людей, на разных стадиях инкубации (от 1 до 14 дней).

Симптомы: 1 018 - 1 080.

Если к этой дате путешествие между всеми странами не будет остановлено, а границы не закрыты, эпидемия ускорится и мы получим следующие цифры:

5 февраля, 00:00 по Гринвичу: 139 000 - 226 500 инфицированных людей, находящихся на разных стадиях инкубации ( От 1 до 14 дней).

Симптомы: 1790 - 1900.

С этой даты пандемия больше не может сдерживаться без введения полного карантина, по крайней мере, для всех крупных городов по всему миру. Экономический крах и паника. Может существовать огромная разница между количеством зараженных в этой модели и вероятной реальностью, потому что большинство стран недостаточно развиты, и вирус затронет их гораздо больше Индию и Юго-Восточную Азию. Если полный или, наконец, частичный карантин не будет введен к 5 февраля, в крупных городах мира пандемия будет распространяться следующим образом (с поправкой на более высокий R0 и более высокий индекс вероятности распространения инфекции) имея в виду то, что цифры будут средние:

6 февраля: 345 000, зараженные 3600 с симптомами

7 февраля: 690 000, зараженные 7500 с симптомами

8 февраля: 1 435 000/15 600

9 февраля: 2 980 000/27 456

10 февраля: 6 240 000/57 100

11 февраля: 12 979 000/118 100

фев 12: 27 990 000 / 245 600

13 февраля: 58 220 000/509 600

14 февраля: 121 970 000/1 060 000

15 февраля: 253 697 000/2 204 800

С 16 февраля несколько систем здравоохранения по всему миру рухнут. Больницы будут переполнены и не смогут проводить тестирование и лечение большинства пациентов. Социальная структура полностью разрушится, и у правительств, если они отложат карантин, не будет другого выбора, кроме как запереть сотни миллионов людей в крупных и средних городах в то время, как сотни миллионов в небольших городах станут самоизолированными.

Однако закончить друзья, хотелось бы тем, что есть все онсования говорить о том, что эта модель уверенно потерпит фиаско и неудачу. Тем более, об этом нам свидетельствует опыт последних лет, где было многое:

В нашем первом посте про трехмерное моделирование вирусов мы перечислили основные стадии процесса и рассказали о том, с чего мы начинаем и как собираем исходную информацию. В этой заметке мы расскажем о следующем этапе работы — о создании моделей отдельных молекул, из которых впоследствии будет собрана целая частица.

Компоненты вирусной частицы Гриппа A/H1N1

Вирусная частица — это молекулярный механизм, решающий две принципиальные задачи. Во-первых, частица должна обеспечить упаковку вирусного генома и его защиту от деструктивных факторов среды, пока вирус путешествует из клетки, в которой он собрался, к клетке, которую он сможет заразить. Во-вторых, частица должна быть способна присоединиться к заражаемой клетке, после чего доставить вирусный геном и сопутствующие молекулы внутрь, чтобы запустить новый цикл размножения. Задач не очень много, поэтому вирусы, за редким исключением, могут позволить себе быть довольно экономными в том, что касается структуры.

В частности, геном большинства вирусов невелик и кодирует не очень много белков, нередко это число меньше 10. При этом вирус может заставить клетку синтезировать большое количество однотипных белков, из которых потом соберется вирусная оболочка — капсид. Таким образом, вирусные частицы обычно состоят из большого числа одинаковых элементов, которые связываются друг с другом как детали конструктора, часто образуя регулярные и симметричные структуры. Так, очень многие, хоть и не все вирусные упаковки или их фрагменты имеют спиральную или икосаэдрическую форму.

Примеры вирусных капсидов с икосаэдрической симметрией. Молекула бактриородопсина в правом нижнем углу — для сравнения. (Иллюстрация из обзора).

Для сборки модели вируса принципиально важно знать, как устроены отдельные белки общей структуры и как они друг с другом связываются, эту структуру формируя. Современная наука владеет целым набором методов, которые могут дать ответы на эти вопросы, однако ни один из подходов, к сожалению, не является универсальным и решает только часть задач которые стоят перед нами при создании научно достоверных моделей вирусов с атомной детализацией.

Напомним, что белки — это полимерные молекулы, состоящие из последоватльно связанных между собой мономеров — аминокислот. В водных растворах белки обычно сворачиваются в сложные трехмерные глобулы (почти как головоломка “Змейка Рубика”), форма которых зависит от аминокислотного состава и некоторых других факторов. Пространственное строение этих глобул определяют в основном методами рентгеноструктурного анализа и ЯМР-спектроскопии. Также в последнее время к этой задаче позволяет подойти электронная микроскопия.
В целом, методы определения пространственной структуры молекул сложны и имеют целый набор ограничений, поэтому далеко не все вирусные белки описаны полностью. Так, рентгеноструктурный анализ предполагает наличие кристалла, через который пропускается рентгеновское излучение. Атомы кристалла провоцируют дифракцию рентгеновских лучей, по картине которой можно оценить распределение электронных плотностей в кристалле, а по этим данным уже восстановить расположения конкретных атомов. Этот метод дает разрешение вплоть до чуть более 1 ангстрема (0,1 нм), однако в случае белков проблема заключается в том, что далеко не все из них можно кристаллизовать. Особенно сложным это оказывается, если белок имеет гибкие подвижные или заякоренные в мембране фрагменты.

ЯМР-спектроскопия основана на явлении ядерного магнитного резонанса и позволяет описывать строение белков в растворе. Этот подход выявляет набор возможных положений атомов в молекуле и, в отличие от предыдущего метода, дает возможность оценить степень гибкости тех или иных ее участков. Но ЯМР-спектроскопия хорошо работает только для сравнительно небольших молекул, поскольку крупные белки дают слишком много шума.

Электронная микроскопия позволяет описать строение крупных молекулярных комплексов, что бывает очень полезно, когда речь идет о вирусах. Для многих симметричных структур можно получить большой набор изображений под разными углами, проанализировав которые можно воссоздать трехмерную картину. Для отдельных объектов разрешение, получаемое в результате применения разных вариантов электронной микроскопии (до 4-5 ангстрем), оказывается не многим хуже разрешения рентгеноструктурного анализа, хотя обычно для получения полной информации приходится совмещать разные подходы и, например, “вписывать” структуры отдельных белков в карты электронных плотностей, получаемые при помощи электронной микроскопии.

Структуры тримера белка оболочки ВИЧ (красные и голубые фрагменты молекул) в комплексе с участком одного из антител к этому белку (зеленые и желтые фрагменты), вписанные в карту электронной плотности, полученную методом крио-электронной микроскопии с разрешением 9 ангстрем. Из статьи Structural Mechanism of Trimeric HIV-1 Envelope Glycoprotein Activation.

Как мы писали в прошлом посте, получаемые структуры систематизируются и хранятся в базе данных Protein Data Bank. При этом в формате *.pdb записываются координаты атомов, и существует целый набор программ, позволяющих эти данные визуализировать и работать с такими структурами. Среди них, например VMD, Chimera, PyMol и десятки других.

Скриншот текстового отображания файла в формате *.pdb. Описываются координаты отдельных атомов в аминокислотах белка.

Программы могут отображать белки несколькими способами. Помимо простого отображения атомов сферами разного диаметра, соответствующего ван-дер-ваальсовым радиусам атомов, существует возможность показать отдельные связи, поверхность молекулы, а также изгибы аминокислотной цепочки при помощи структур, напоминающих ленты (ribbon diagram), которые наглядно демонстрируют, где в белке аминокислоты образуют альфа-спирали, где бета-слои, а где неструктурированные участки.

Различные варианты визуализации структуры наружней части гемагглютинина вируса гриппа в программе Chimera.

В качестве отступления, надо сказать, что программы, в которых обычно работают ученые, визуализируя отдельные молекулы или белковые комплексы, чаще всего позволяют получить лишь довольно примитивные с эстетической точки зрения результаты (достаточно, например, посмотреть на несколько скриншотов из программы VMD). Принципиально более широкие возможности открываются, если импортировать модели молекул в программы, которые используют профессиональные дизайнеры и специалисты компьютерной трехмерной графики. Эти программы в сочетании с плагинами, улучшающими качество рендера, позволяют получать действительно интересные и привлекательные визуализации. Мы еще расскажем об этом в следующих постах. Пока просто приведем пример:

Изображения молекулы иммуноглобулина G.

Шаблоны для моделирования нейраминидазного комплекса вируса гриппа. А — фрагмент мономера нейраминидазы N2 из структуры 2AEP в базе данных PDB, B — “стебель” гемагглютинин-нейраминидазы парагриппа (3TSI), С — трансмембранный пептид 2LAT. D — финальная полученная модель.

Окончательная модель белка обычно создается с учетом известных структур его фрагментов, найденных разными методами шаблонов, а также моделей от сервера I-Tasser. Для этого используется программа Modeller. Она позволяет строить модель по гомологии с использованием одного или нескольких шаблонов, а также вносить дополнительные модификации, например, создавать дисульфидные связи в заданных местах.

Другим важным аспектом строения вирусов, информация о котором в научной литературе часто оказывается не полна, является взаимодействие между отдельными белками. В нашем случае от этого зависит то, какими поверхностями модели отдельных белков будут контактировать друг с другом и другими компонентами вириона в финальной модели. Информацию о взаимодействиях тоже позволяет уточнить структурная биоинформатика.

Программа докинга не моделирует естественный процесс образования комплекса, это было бы слишком медленно и ресурсоемко, а перебирает варианты взаимного положения двух или более молекул в поисках наилучшей структуры. При докинге обычно большую молекулу в комплексе называют рецептором, а меньшую — лигандом. Для определения качества структуры комплекса лиганда с рецептором используются различные оценочные функции. В идеале в качестве такой функции должна выступать свободная энергия системы, но она слишком сложно вычисляется, поэтому применяют различные эмпирические псевдопотенциалы, учитывающие потенциальную энергию (которая как раз вычисляется просто), площадь контакта лиганда и рецептора, соответствие различным правилам, которые исследователи вывели из анализа большого числа комплексов, и всякие загадочные слагаемые, не имеющие физического смысла, но улучшающие результат программы при испытании на большом количестве известных комплексов. Поиск минимума такого псевдопотенциала в современных программах обычно происходит с помощью различных вариаций метода Монте-Карло и генетических алгоритмов. В настоящее время существует множество программ молекулярного докинга (наиболее известные из них — Dock, Autodock, GOLD, Flexx, Glide), отличающиеся оценочными функциями, методами минимизации и дополнительными возможностями. При этом во время поиска молекулы рецептора и лиганда могут как оставаться неподвижными (такой тип докинга называется жестким), так и несколько менять конформацию (гибкий докинг). Очевидно, что второй вариант более ресурсоемкий, но и результаты такого поиска обычно правдоподобнее. Докинг малых молекул к белкам сейчас является стандартным этапом разработки новых лекарственных препаратов. Можно, например, провести докинги для 10 миллионов лигандов, и выбрать сотню наиболее перспективных соединений для дальнейшей экспериментальной работы — это называется виртуальный скрининг.

Помимо исследований небольших молекул, докинг может быть использован и для построения белок-белковых и белок-нуклеотидных комплексов. Для этих целей также разработано большое количество программ и онлайн-сервисов (ZDOCK, pyDOCK, HEX). Например, в ходе нашей работы над вирусом папилломы человека (ВПЧ) мы столкнулись с тем, что, несмотря на наличие полной структуры внешнего слоя капсида, образованнного белком L1, совершенно не было информации о строении белка L2, который в капсиде расположен ближе к геному, а соответственно, нет данных о том, как пентамеры L1 взаимодействуют с молекулами L2. Мы построили модель белка L2 по гомологии, используя сервер Tasser, после чего провели докинг в программе HeX. В ходе докинга роль рецептора выполнял пентамер L1. Именно на его поверхности проводился поиск оптимального места посадки L2. При этом все структуры оставались неподвижными. Т.е. использовался метод жесткого докинга. В результате была получена правдоподобная структура комплекса пентамера, собранного из L1 и минорного белка L2.

Наконец, биоинформатическими методами можно пытаться восстановить то, какие изменения в структуру вирусных белков вносит сама клетка, в которой они образуются. Большинство белков после синтеза подвергаются дополнительным химическим посттрансляционным модификациям (ПТМ), которые могут серьезно влиять на выполняемые белком функции. Среди таких модификаций фосфорилирование, убиквитинирование, гликозилирование, нитрозилирование, внесние разрывов и другие химические изменения. Многие поверхностные белки вирусов гликозилированы, причем эта модификация имеет непосредственное значение для выполнения основной функции поверхностных белков вируса — связывания с клеточными рецепторами. С другой стороны, белки вирусных матриксов — слоев, которые встречаются непосредственно под липидными оболочками некоторых вирусов, для заякоривания в мембране часто должны быть связаны, например, с миристиловой кислотой — небольшой гидрофобной молекулой, облегчающей взаимодействие белков с липидами. Таким образом, в нашей работе модификации белков тоже требуют внимания.
В настоящее время возможные ПТМ достаточно сложно предсказываются. Основные существующие методы и сервисы основаны на поиске соответствующей экспериментальной информации для сходных белков или поиске в последовательности исследуемого белка небольших участков, характерных для того или иного типа модификации.
В нашей работе при подготовке моделей мы пользуемся экспериментальной информацией, отраженной в соответствующей записи базы данных UNIPROT.

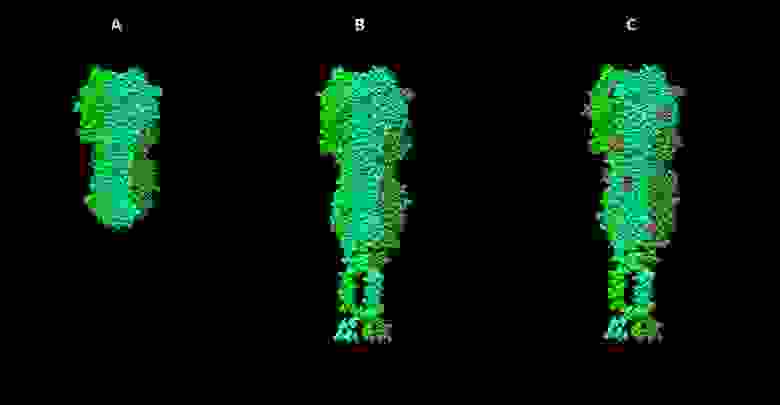
Стадии работы над моделью гемагглютинина вируса гриппа. А — визуализация структуры 3ZTJ из базы данных PDB. B — модель гемагглютинина вируса гриппа H1N1, построенная на основе гомологии с 3ZTJ с достраиванием трансмембранных участков молекулы. С — модель с учетом посттрансляционных модификаций (гликозилирования).

Последнее, о чем хочется упомянуть, — это то, что при подготовке новых моделей белков и, особенно, их комплексов, необходимо проводить оптимизацию структур. Наиболее простым методом оптимизации является минимизация энергии. Она используется для достаточно быстрого “спуска” системы в локальный минимум потенциальной энергии. Эту манипуляцию желательно проводить после каждой модификации структуры молекул. Она позволяет избежать таких неприятностей, как перекрывание атомов или появление неправильных длин связей. Различные методы минимизации энергии предусмотрены практически в любом программном пакете молекулярного моделирования.
Стоит отметить, что данный метод позволяет провести лишь предварительную и очень грубую оптимизацию. Для более точной подготовки пространственных структур используются методы молекулярной динамики или квантовой механики. Последние, например, используются для наилучшей оптимизации структуры небольших молекул лигандов и наиболее точных расчетов энергии межмолекулярных взаимодействий. Но, наибольшая точность, что вполне логично, связана с более ресурсоемкими вычислениями, что делает эти методы практически неподъемными в применении к большим биологическим макромолекулам.
Оценить поведение и стабильность структур достаточно массивных молекул, таких как полипептиды и нуклеиновые кислоты позволяют методы молекулярной динамики.
Метод молекулярной динамики заключается в изучении поведения атомов и молекул и их движений во времени. Расчеты молекулярной динамики позволяют, например, исследовать стабильность как отдельных молекул, так и их комплексов, позволяют оценить значимость возможных конформационных перестроек, влияние точечных мутаций и многое другое. Современные методы анализа результатов симуляций молекулярной динамики позволяют получить самые подробные сведения о поведении во времени как отдельных атомов, так и всей исследуемой системы.

В зависимости от того, насколько хорошо изучены белки того вируса, модель которого мы хотим создать, каждый раз приходится подбирать подходы для достройки и оптимизации моделей всех белков и их взаимодействий. После того, как все структуры получены, можно приступать к сборке полной модели. О том, как это делается, мы расскажем в следующих постах серии о создании научно достверных моделей вирусов человека.

PS:
Ставшая лидером в опросе прошлого поста тема Медицинская анатомическая иллюстрация — история изучения тела человека в работах иллюстраторов 5 столетий будет следующей. С потрясающими гравюрами, восковым моделями прошлого века, пластификатами трупов, атласами выдающся исследователей, 3Д реконструкциями на основе послойных срезов замороженного смертника, интерактивными приложениями и работами современных медицинских иллюстраторов. Скоро.