Математическая модель вирусной инфекции

Аннотация научной статьи по компьютерным и информационным наукам, автор научной работы — Улыбин Андрей Владимирович

ПРОВЕДЕН АНАЛИЗ СУЩЕСТВУЮЩИХ МОДЕЛЕЙ РАСПРОСТРАНЕНИЯ ИНФЕКЦИЙ . ПРЕДЛАГАЕТСЯ ИСПОЛЬЗОВАНИЕ АГЕНТНОГО ПОДХОДА ДЛЯ МОДЕЛИРОВАНИЯ ДАННОГО ПРОЦЕССА. ПРЕДСТАВЛЕНА ИМИТАЦИОННАЯ МУЛЬТИАГЕНТНАЯ МОДЕЛЬ РАСПРОСТРАНЕНИЯ ИНФЕКЦИИ.

Mathematical model of infection propagation

The analysis of existing models of propagation of infections is carried out. The usage agent based approach for modeling of the given process is offered. The imitative multi-agent model of propagation of infection is presented.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РАСПРОСТРАНЕНИЯ ИНФЕКЦИИ

Ключевые слова: агент; модель; имитационное моделирование; мультиагентный подход; модель распространения инфекции.

Проведен анализ существующих моделей распространения инфекций. Предлагается использование агентного подхода для моделирования данного процесса. Представлена имитационная мультиагентная модель распространения инфекции.

Принципы моделирования социальных и эпидемиологических процессов существенно отличаются от моделирования в естественных науках. Здесь нет твердо установленных экспериментом и практикой зависимостей, которые всегда остаются справедливыми и не изменяются. При построении моделей таких процессов необходимо учитывать изначальную неточность задания всех данных, отсутствие четкого математического описания переменных и параметров, используемых при моделировании. Важно понимать возможность отклонения статистических данных от их реальных значений.

В качестве наиболее подходящего аппарата для моделирования процессов в эпидемиологии предполагается имитационное моделирование с использованием мультиагентного метода. Он позволяет, задавшись начальными параметрами по каждому типу объектов, а также системой правил, согласно которой объекты взаимодействуют друг с другом и окружающей средой, вычислить динамические закономерности развития инфекции и выявить наиболее существенные свойства агентов, способствующих изменению темпов распро-

странения. Преимуществом данного подхода является то, что учитываются индивидуальные свойства каждого объекта, составляющего сложную систему. Динамика сложного процесса представляет собой результат функционирования и взаимодействия относительно простых объектов [3]. Основная задача аналитика заключается в формулировке правил взаимодействия.

Необходимо отметить, что мультиагентный подход применялся для исследования процессов распространения инфекций как в России, так и за рубежом. Учеными Guo Zaiyi, Han Hann Kwang и Tay Joc Cing была разработана модель заражения клеток ВИЧ-инфекцией на основе агентного подхода [4]. Данная модель направлена на исследование распространения клеток ВИЧ-инфекции внутри одного организма и не предназначена для изучения распространения инфекции между людьми. Одним из известных способов моделирования распространения инфекций и эпидемий является имитационное моделирование на основе клеточных автоматов [5]. С использованием мультиагентного подхода была изучена динамика распространения ВИЧ-инфекции среди мужчин-гомосексуалистов в Амстердаме [6]. Данная модель рассматривает распространение инфекции в одной группе риска, необходимо отметить, что такой подход часто встречается при моделировании.

Многие приемы, используемые при применении мультиагентного подхода, разработаны в настоящее время в недостаточной степени. В частности, не решались задачи параметрической идентификации указанных моделей, нахождения необходимого числа агентов, обеспечивающих репрезентативность вычислительных экспериментов, проверки мультиагентных моделей на адекватность. По этой причине разработка новых математических моделей, алгоритмов и программ, предназначенных для использования мультиагентного подхода при анализе различных систем, представляет собой актуальную научную задачу.

Данная работа направлена на разработку мультиа-гентной модели распространения инфекции, на основе которой предполагается создание универсального симулятора для моделирования различных инфекций.

ОСНОВНЫЕ ДОПУЩЕНИЯ, ИСПОЛЬЗУЕМЫЕ ПРИ МОДЕЛИРОВАНИИ

Итак, необходимо разработать мультиагентную модель распространения инфекции, позволяющую учесть индивидуальные свойства объектов и проводить вычислительные эксперименты по исследованию процесса распространения.

Основные допущения, принятые при разработке математической модели и алгоритмов, лежащих в основе программного комплекса, имеют следующий вид.

1. Моделирование осуществляется на ограниченной территории, где существует вероятность взаимодействия любого агента с любым другим из системы, т. е. У01,02 е С ^ ЗР(01 П 02) Ф 0 .

2. Время в модели дискретно. Единицей времени является одна итерация. В реальном времени она может представлять собой один день, месяц, год и т. п. в зависимости от значений параметров модели. Отсчет времени начинается с нуля итераций. Шаг времени равен единице.

3. В начальный момент времени формируется множество агентов системы согласно статистическим данным. Свойства и параметры агентов определяются на стадии формирования всего множества.

4. Максимальная продолжительность жизни агента задается количеством итераций, по истечении которого агент умирает. Максимальная продолжительность жизни может быть изменена в процессе моделирования в случае инфицирования агента.

5. Все агенты разбиваются на типы, определяющие его отношение к инфекции: здоровый агент, инфицированный агент, носитель инфекции (способный к инфицированию других агентов, но при этом не испытывающий негативного влияния инфекции). Здоровые агенты в свою очередь могут обладать иммунитетом либо быть склонными к заражению.

6. Для каждого типа объектов определяется система правил, взаимодействие по которым определяет характер динамики распространения инфекции.

7. Взаимодействие одновременно возможно только между двумя агентами системы. То есть невозможно такое взаимодействие, в результате которого изменяются параметры нескольких (более двух) агентов.

8. Замена типа происходит при взаимодействии объектов разных типов. Результатом взаимодействия является тип, определяющий статус инфицирования объекта.

ИМИТАЦИОННАЯ МУЛЬТИАГЕНТНАЯ МОДЕЛЬ РАСПРОСТРАНЕНИЯ ИНФЕКЦИИ

Общее количество инфицированных агентов на любой итерации всегда можно рассчитать по формуле:

где Кщ[ - общее количество инфицированных, К - количество инфицированных в результате внутренних процессов, К - количество инфицированных иммигрантов, ке - количество инфицированных эмигрантов.

Количество инфицированных в результате внутренних процессов рассчитывается по формуле:

где К- количество инфицированных различными

путями заражений, Б - количество умерших среди инфицированных, 1 - г-й путь передачи инфекции.

В начальный момент времени имеется множество М - множество объектов различного типа: М = <<С1>,<С2>. <Ср>>, где р - количество типов

где Ск - множество объектов типа к, пк - общее количество объектов типа к в начальный момент времени.

Каждому объекту из множества, определенного выражением (1), соответствует следующий набор параметров:

где sk - пол объекта, ак - возраст объекта в началь-

ный момент времени, атг - максимальная продолжительность жизни объекта, wk - количество взаимодействий объекта с другими объектами, рк - вероятность

инфицирования при взаимодействии, Ик - продолжительность жизни инфицированного объекта.

Функционирование объектов подчинено следующим правилам.

Возникновение г-го объекта типа к в момент времени t+1 определяется выражением (2), а его гибель выражением (3).

(Ск )г ^ (Ск - <сг >Х+1 • (3)

Система правил (4) определяет изменение ак - возраста объекта типа к за единицу времени. Согласно нашим допущениям, время дискретно и измеряется в итерациях. На каждой итерации будем увеличивать возраст объекта на единицу времени. Согласно второму правилу системы, необходимо исключить объект из множества объектов типа к, если отведенный ему максимальный срок жизни уже истек.

(ск Ь ^ (ск)( : (ак), = (ак)м +1

(ак)<>атк ^ (Ск)<^ (Ск- <ск >^+1, (4) к = 1, р, г = 1, пк.

Выражение (5) позволяет уменьшать максимальный срок жизни объектов типа к на заданное количество итераций (максимальная продолжительность жизни г-го объекта после изменения типа) в случае изменения типа объекта в результате взаимодействия объектов разных тигаж

(ak) + h, (ak) + hi ami.

Вероятность нового инфицирования при взаимодействии двух агентов существует, если выполняется условие:

где элементарное событие A - это взаимодействие здорового агента с инфицированным агентом A є W , W -пространство элементарных событий при взаимодействии агентов; элементарное событие B - передача инфекции в результате взаимодействия B є Q, Q - пространство элементарных событий при передаче инфекции; i = 1, n,, j = 1, nm , nk - количество объектов заданного типа k, nm - количество объектов заданного типа m.

Замена i-го объекта типа k на j-й объект типа m происходит при изменении статуса инфицирования в соответствии с выражением:

(Ck )t ^ (Ck - )t+1 (Cm)t ^ (Cm + )t+/

Итак, для имитационного моделирования распространения инфекции на основе агентно-ориентированного подхода необходимо определить начальные параметры по каждому типу объектов.

Имитационная модель распространения инфекции реализована в среде Lazarus на платформе хб4.

Для проведения вычислительных экспериментов были использованы данные Федерального научнометодического Центра по профилактике и борьбе со СПИДом по распространению ВИЧ-инфекции в России, данные Территориального органа Федеральной службы государственной статистики по Тамбовской области и Управления здравоохранения Тамбовской области по распространению туберкулеза в Тамбовской области [8, 9]. Исходное количество агентов, а также их свойства задавались согласно статистическим данным.

В табл. 1 представлены результаты по моделированию распространения туберкулеза в Тамбовской области.

Относительная погрешность вычислений при этом составила 4,1 %. Результаты моделирования на данных ВИЧ-инфекции были ранее представлены в статье [7]. Было получено, что количество инфицированных агентов в результате эксперимента превосходит статистические показатели. Относительная погрешность вычислений при этом составила 15,5 %. Однако анализ процесса распространения инфекции показал, что характер изменения динамики по модели соответствует данным

Кумулятивное количество новых случаев заболеваний туберкулезом в Тамбовской области по годам

Год Данные Результат

Также необходимо обозначить проблему нехватки вычислительных ресурсов, т. к. для моделирования распространения инфекции в пределах всей России количество агентов имеет порядок 108. Для целей данной работы использовался сервер на базе двух процессоров 1Пе1 Хеоп Е5520 с 24 Гб оперативной памяти и дисковым массивом га1(110 (4хБЛ815к). Наиболее предпочтительным вариантом решения проблемы нехватки вычислительных ресурсов предполагается использование распараллеливания вычислений.

Необходимо отметить, что проблема распространения инфекций остается актуальной и требует выявления основных причин и факторов, способных снизить темпы распространения. В данной работе для решения этих задач предлагается использовать дискретную модель распространения инфекции с использованием мультиагентного подхода. Обозначены основные допущения, используемые при моделировании, произведена формализация имитационной модели распространения инфекции на основе агентного подхода. Вычислительные эксперименты, даже при значительном уп-

рощении модели (что отражено в допущениях), позволяют проводить исследования процесса распространения. Таким образом, можно рекомендовать мульти-агентный подход для имитационного моделирования распространения инфекций и иных социальных процессов, в которых поведение сложной системы представляет результат взаимодействия составляющих ее объектов.

1. Perelson A.S. Modelling viral and immune system dynamics // Nature Reviews Immunology. 2002. № 1. P. 28-3б.

2. Жуковский Е.С., Шиндяпин А.И., Плужникова Е.А. Математическая модель динамики распространения ВИЧ/СПИД, учитывающая вероятность прекращения антивирусного лечения // Гаудеамус. Актуальные проблемы информатики и информационных технологий. Материалы XIV-й международной научно-практической конференции. 2010. № 2. С. 350-352.

3. Замятина Е.Б. Современные теории имитационного моделирования: Специальный курс. Пермь: ПГУ, 2007. 119 с.

4. Cing T.J., Kwang H.H., Zaiyi G. Sufficiency Verification of HIV-1 Pathogenesis Based on Multi-Agent Simulation // GECCO. 2005. P. 305-312.

5. Куравский М.Л. Моделирование распространения эпидемий // Экологические системы и приборы. 2003. № 2. С. 49-54.

6. Shan A.M., Sloot P.M.A., Quax R., Zhu Y., Wang W. Complex Agent Networks explaining the HIV epidemic among homosexual men in Amsterdam // Mathematics and Computers in Simulation. 2010. V. 80. № 5. P. 1018-1030.

7. Арзамасцев А.А., Улыбин А.В. Имитационное моделирование развития инфекции с использованием агентного подхода // Вестник Тамбовского университета. Серия Естественные и технические науки. Тамбов, 2010. Т. 15. № 2. С. 614-619.

Поступила в редакцию 12 ноября 2010 г.

Ulybin A.V. Mathematical model of infection propagation The analysis of existing models of propagation of infections is carried out. The usage agent based approach for modeling of the given process is offered. The imitative multi-agent model of propagation of infection is presented.

Key words: agent, model, simulation modeling, multi-agent based approach, model of infection propagation.

Как математика помогает бороться с эпидемиями

Эпидемии издавна угрожали человечеству, и только в ХХ веке были разработаны эффективные средства борьбы с инфекциями. К числу этих средств принадлежат и системы дифференциальных уравнений — математика помогает моделировать распространение эпидемий и помогает понять, как следует с ними бороться. Это наш третий материал о самых интересных дифференциальных уравнениях и о том, где и как они применяются (предыдущие материалы можно прочитать здесь и здесь). Если вы читаете нас с телефона, переключайте страницу на десктопную версию, так вы сможете увидеть интерактивный график целиком.

В XXI веке мир уже успел столкнуться с эпидемией птичьего гриппа в Юго-Восточной Азии (в 2013 году) и вспышкой заболеваний лихорадкой Эбола в Африке (2015). Но в истории человечества бывали и куда более масштабные эпидемии.

В 551-580 годах нашей эры в Восточной Римской империи разразилась первая задокументированная пандемия чумы, получившей название Юстиниановой, в результате которой погибло около 100 миллионов человек (по другим данным, жертв могло быть значительно меньше). Спустя еще 800 лет в Евразию и Северную Африку пришла Черная смерть — пандемия чумы, сразившая от трети до половины тогдашнего населения этих регионов.

В результате Первой мировой войны, вызвавшей перемещение большого количества людей, в 1918 году распространился испанский грипп, охвативший более 500 миллионов человек и погубивший каждого десятого заболевшего. Эта пандемия стала самой масштабной за всю историю человеческой цивилизации, коснувшись до 30 процентов населения Земли.

В медицинской классификации эпидемией называют прогрессирующее распространение инфекционного заболевания на уровне выше среднего на данной территории. В случае распространения эпидемии на большие территории или территории многих стран говорят о пандемии.

Для эпидемии среди животных применяется термин эпизоотия, а среди растений — эпифития. Этим явлениям ученые также уделяют большое внимание, поскольку они, в свою очередь, помогают понять механизм распространения инфекций.

Изучение механизмов развития и распространения эпидемий является важным способом борьбы с заболеваниями наряду с поиском новых лекарств, вакцинацией и профилактическими мерами. На помощь медикам пришли математики — для этого им пришлось объединить дифференциальные уравнения и теорию вероятности.

Первую попытку использовать математический аппарат для исследования механизмов распространения заболеваний предпринял Даниил Бернулли, ранее открывший первые законы гидродинамики. Следующий шаг сделал Уильям Фарр, применивший в 1840 году нормальное распределение к анализу смертности от оспы.

В рамках этой модели с помощью систем дифференциальных уравнений (при условии непрерывности времени и большой популяции) или разностных уравнений (при дискретном времени и ограниченной популяции) описывается динамика распространения заболевания.

SIR–модель получила заслуженную популярность в силу простоты построения и использования. Ее применение позволяет точно моделировать эпидемии гриппа и других заболеваний в больших городах, вводить новые параметры и анализировать разные сценарии.

Система уравнений SIR:

S(t) — численность восприимчивых индивидов в момент времени t;
I(t) — численность инфицированных индивидов в момент времени t;
R(t) — численность переболевших индивидов в момент времени t;
β — коэффициент интенсивности контактов индивидов с последующим инфицированием;
γ — коэффициент интенсивности выздоровления инфицированных индивидов.

Первое уравнение системы означает, что изменение числа здоровых (и при этом восприимчивых к заболеванию) индивидуумов уменьшается со временем пропорционально числу контактов с инфицированными. После контакта происходит заражение, восприимчивый переходит в состояние инфицированного.

Второе уравнение показывает, что скорость увеличения числа заразившихся растет пропорционально числу контактов здоровых и инфицированных и уменьшается по мере выздоровления последних.

Третье уравнение демонстрирует, что число выздоровевших в единицу времени пропорционально числу инфицированных. Иначе говоря, каждый заболевший через некоторое время должен поправиться.

описывает неизменность численности популяции (и не учитывает случаи смерти от заболевания).

Графики решения выглядят так (это интерактивный график, в нем можно регулировать параметры β и γ):

Здесь синяя линия — число восприимчивых индивидов, красная — инфицированных, зеленая — переболевших.

Красный график интенсивности эпидемии, показывающей количество одномоментно болеющих индивидов, определяется параметром:

В 2012 году британская компания Ndemic Creation выпустила игру “Plague Inc.”, биологический симулятор эпидемий. По сценарию игры необходимо развить одно из выбранных заболеваний настолько, чтобы оно уничтожило жизнь на Земле.

На базовых уровнях игры распространение заболевания происходит в точном соответствии с моделью SIR. Если принять, что вместо выздоровления происходит гибель организма, то зеленый график становится графиком числа умерших — каждый игрок может увидеть его при успешном прохождении уровня.

“Plague Inc.” является одной из лучших стратегий среди существующих на рынке и на протяжении многих лет пользуется популярностью у десятков миллионов поклонников.

SIR-модель перестает работать в случае необходимости учитывать неоднородность популяции (например, различную плотность населения в разных районах), разные пути передачи инфекции и факторы случайности, значимые в малых популяциях и на начальной фазе распространения заболевания.

Развитием модели SIR стали, в частности, следующие модели:

Именно по этой модели развиваются по-настоящему опасные эпидемии, поскольку длительный инкубационный период может препятствовать своевременному обнаружению заболевания. В этом случае есть риск, что заболевание охватит значительное число индивидуумов в популяции.

μ — уровень смертности;
α — величина, обратная среднему инкубационному периоду заболевания;
E(t) — численность индивидов — носителей заболевания в момент времени t.

Как и в модели SIR, первое уравнение системы означает, что изменение числа здоровых (и при этом восприимчивых к заболеванию) индивидуумов уменьшается со временем пропорционально числу контактов с инфицированными. После заражения здоровый индивид переходит в состояние контактного по данному заболеванию, или носителя инфекции.

Второе уравнение вносит задержку по времени при переходе из состояния контактного в состояние инфицированного (больного). Это происходит через время, равное инкубационному периоду болезни.

Четвертое уравнение демонстрирует, что число выздоровевших в единицу времени пропорционально числу инфицированных. При этом в каждом состоянии индивидуум может погибнуть, что учитывает коэффициент μ в каждом уравнении.

Иначе говоря, в каждый момент времени каждый индивидуум с определенной вероятностью может заразиться, через некоторое время — заболеть, а затем поправиться либо погибнуть.

Численность популяции N = S + E + I + R при этом не является постоянной с течением времени.

Интенсивность эпидемии описывает базовый коэффициент воспроизведения:

Например, построим симуляцию, использовав следующие параметры:

На площади 20 × 20 размещены 100 индивидуумов (заполнение 25 процентов);
Индивидуумы на каждом шаге перемещаются с вероятностью 80 процентов, в случае контакта здорового индивидуума (зеленая точка) с инфицированным (красная точка) происходит заражение с вероятностью 50 процентов;
Заражение длится 6 дней, в течение которых возможна смерть организма с вероятностью 50 процентов либо полное выздоровление с приобретением иммунитета;
В момент начала эпидемии примем, что инфицированы 5 процентов организмов и еще 5 процентов имеют иммунитет;
Модель дискретная, один день = один шаг модели.

С помощью моделирования мы видим, что 49 организмов из 100 погибнут в результате эпидемии длительностью в 29 дней.

Симуляция эпидемии с заданными параметрами

Epidemic Simulator позволяет моделировать результаты эпидемий при различных плотности популяции, заразности, летальности и устойчивости заболеваний.

Вместе первое и второе уравнение означают, что число здоровых и больных в сумме не меняется, а число заражений пропорционально числу контактов здоровых и больных.

Второе уравнение описывает изменение числа заболевших в единицу времени, которое пропорционально числу заражений (числу контактов здоровых и инфицированных индивидуумов) за вычетом числа выздоровлений.

График развития заболевания в соответствии с этой моделью выглядит так (график интерактивный, можно регулировать параметры β и γ):

Синяя линия — число восприимчивых индивидов, красная — инфицированных в текущий момент.

Эта модель, построенная для заболевания с инкубационным периодом и учитывающая иммунитет детей, приобретенный внутриутробно, — одна из самых сложных для анализа в силу наличия большого числа независимых параметров. Система уравнений для нее выглядит так:

Ученые Самарского национального исследовательского университета и Автономного университета Барселоны разработали математическую модель распространения опасных вирусных инфекций. Разработке посвящена статья, опубликованная в журнале Американского института математических наук Mathematical Biosciences and Engineering (MBE). В публикации рассматриваются различные аспекты распространения инфекций среди животных, но, по мнению ученых, данную модель можно применить и к инфекционным заболеваниям человека, в том числе к коронавирусу.

Модель учитывает множество факторов и постоянно изменяющихся данных, в том числе, например, уровни смертности и рождаемости, отсутствие или наличие иммунитета после выздоровления, сокращение кормовой базы или уменьшение запасов еды, а также явление “мнимого исчезновения”. Динамика процессов описывается взаимосвязанными системами дифференциальных уравнений. Особый акцент в своих исследованиях ученые сделали на математическом моделировании критических ситуаций, возникающих по мере распространения болезни в популяции. Модель демонстрирует возможность и неконтролируемого развития событий в случае взрывного характера распространения вируса.

“В распространении вирусной инфекции можно выделить два различных процесса. Когда речь идет о развитии болезни внутри одного организма, то может иметь место явление “мнимого исчезновения”, когда обнаружить возбудителей заболевания не удается только потому, что время взятия биологического материала для анализов – например, крови, плазмы, тканей – соответствовало периоду мнимого исчезновения. Это перекликается с тем, что у некоторых людей, которых считали выздоровевшими от коронавируса, через некоторое время обнаруживали рецидивы болезни, – отметила профессор Самарского университета Елена Щепакина. – Второй процесс – это распространение инфекции в популяции, особи которой подвержены заболеванию, при этом не имеет значения, идет ли речь о популяции микроорганизмов, животных или людей. Одной из особенностей наших исследований является анализ критических значений параметров и моделирование критических явлений”.

По словам профессора, пояснить понятие критического режима и критических явлений можно на примере из теории горения. Процесс горения может протекать плавно и безопасно, но при изменении параметров горения, когда они заходят за пределы допустимых значений, этот процесс может приобрести очень опасный характер, сопровождаемый так называемым тепловым взрывом.

“Критический режим разделяет режимы опасного и безопасного горения. Именно для моделирования подобных явлений и применяются такие специальные математические объекты как “траектории-утки” и их обобщения – “каскады уток” и “черные лебеди”, – сказала Щепакина. – Применительно к модели распространения вирусной инфекции, которая предложена и изучена в нашей статье, это означает принципиальную возможность неконтролируемого развития событий. Поэтому мы считаем, что никакая предосторожность в текущей ситуации по коронавирусу не может быть излишней”.

Как отметила Щепакина, опубликованная в MBE научная работа входит в целую серию статей, написанных учеными Самарского университета на тему математического моделирования биологических процессов. Теоретические основы этих прикладных исследований изложены в ряде монографий, вышедших в известных научных издательствах как в России (“Наука” и “Физматлит”), так и за рубежом (Springer и SIAM). Авторству самарских ученых принадлежит и выдвинутая около 15 лет назад гипотеза о мнимом исчезновении, касающаяся изменений популяций микроорганизмов.

“Мы выдвинули чисто теоретическую гипотезу, суть которой состоит в следующем. В некоторых микробиологических сообществах может иметь место явление, которые мы назвали эффектом мнимого исчезновения: популяция микроорганизмов может сокращаться до исчезающе малых размеров, а по прошествии некоторого времени ее размеры нарастают, причем взрывным образом, при этом временные промежутки, соответствующие мнимому исчезновению, могут превосходить промежутки, на которых популяция имеет значительные размеры, на несколько порядков”, – рассказала Щепакина.

К этой гипотезе с одобрением отнесся известный микробиолог профессор Майкл Прентис (Michael Prentice), возглавлявший отделение медицинской микробиологии в Национальном университете Ирландии.

“Он привлек наше внимание к известным данным об изменениях в популяции морских фагов, которые полностью подтвердили справедливость гипотезы. В соавторстве с Майклом Прентисом была опубликована первая работа на эту тему, после этого вышли еще несколько статей по данной тематике, а буквально на днях мы получили сообщение, что еще одна статья будет опубликована в специальном выпуске журнала Australian and New Zealand Industrial and Applied Mathematics Journal, который будет посвящен юбилею Грэма Уэйка, известного специалиста по математическому моделированию инфекционных заболеваний из новозеландского университета Мэсси”, – сказала Щепакина.

Пресс-служба Самарского национального исследовательского университета

Детектив: откуда взялся COVID-19 и как перемещается (ENG)

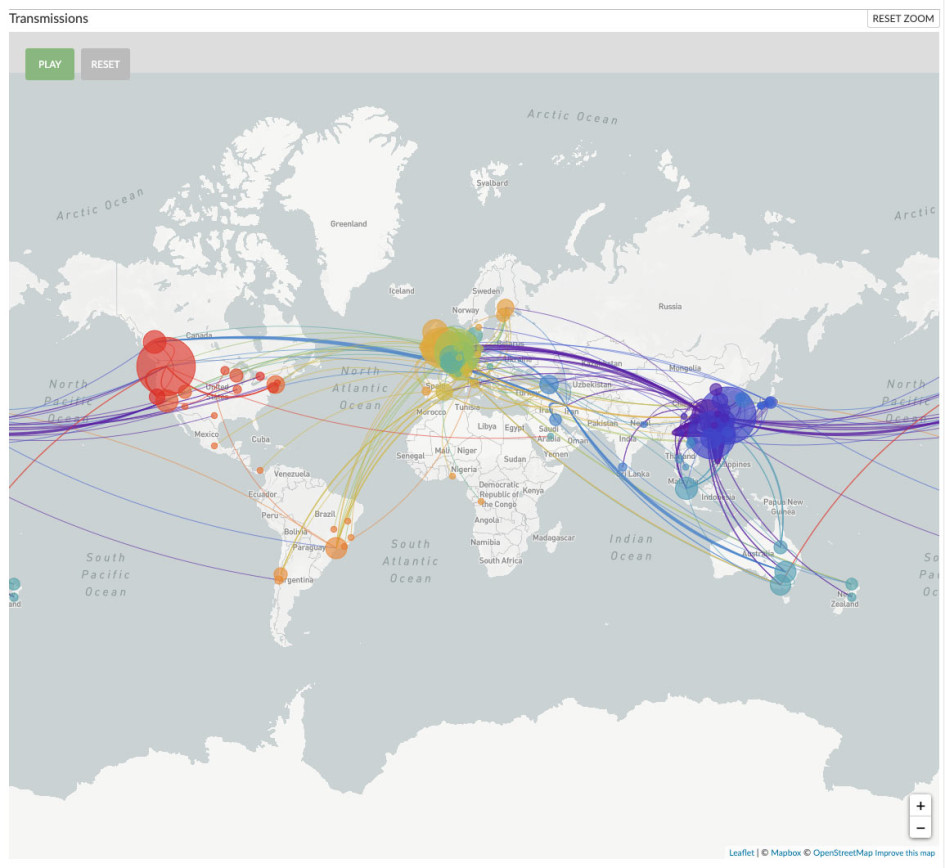
Демография имеет значение (ENG)

Поскольку летальность COVID-19 значительно увеличивается с возрастом пациента, особенности возрастных структур населения могут оказывать значительный эффект на общую смертность от пандемии коронавируса. Демограф Илья Кашницкий оценил этот эффект и отобразил на карте различия в возрастных структурах населения регионов Европы.

За основу взяли данные о летальности пандемии в Италии — первой европейской стране, где ситуация начала развиваться очень быстро, и к 17 марта было зафиксировано уже 2003 смерти. Предположив, что во всех прочих регионах Европы летальность будет такой же как мы наблюдали в Италии, а общее число инфицированных достигнет 2/3 населения (цифра, о которой упоминала в своем обращении Ангела Меркель), рассчитали долю населения с повышенным риском умереть от пандемии. Надо отметить, что эта величина не претендует на роль сколько-нибудь точного прогноза финальной летальности. Допущения при расчетах очень значительны и маловероятны в долгосрочной перспективе. Однако, суть исследования — в сравнении возрастных структур населения. Различия между ними останутся неизменными, даже если повозрастная летальность от COVID-19 окажется существенно отличной от наблюдаемых сейчас в Италии величин, важно лишь, чтобы различия между возрастными группами оставались схожими.

Проведенный анализ позволяет выявить потенциально наиболее уязвимые регионы. Наибольшие потери населения из-за пандемии вероятны в странах и регионах с наиболее возрастным населением — Италия, Германия и Испания. Самый интересный вывод: несмотря на то, что сейчас наибольшее количество зарегистрированных случаев заражения и смертей концентрируется в больших городах, куда вирус пришел раньше, при масштабном неконтролируемом распространении наиболее проблемными станут отдаленные периферийные районы с наиболее пожилым населением. Это еще одна причина, почему карантинные меры, призванные растянуть во времени пик пандемии, чрезвычайно важны, особенно в странах Европы с относительно старым населением.

Источник: Kashnitsky, I. (2020). COVID-19 in unequally ageing European regions. OSF Preprint.

Экспоненциальный рост и эпидемии (ENG, RUS)

Математик объясняет, в какой момент нужно начинать беспокоиться. Эпидемия развивается экспоненциально — это значит умножение на какую-то константу (постоянный коэффициент).

Согласно данным на начало марта число случаев каждый день превышало число случаев в предыдущий день в 1,12—1,25 раз. Изменение количества зараженных изо дня в день складывается из трех цифр: количество зараженных в определенный день (N), среднее количество человек, с которым зараженный может контактировать в определенный день (E), и вероятность каждого контакта стать новым случаем заражения (p). Соответственно, по данным на 6 марта, в среднем каждые 16 дней количество зараженных увеличивалось в 10 раз. Но просто провести восходящий тренд недостаточно: в какой момент рост кривой должен остановиться. И важную роль начинают играть переменные E и p — они должны снижаться, чтобы остановить экспоненциальный рост.

Интерактивная модель: как распространяется вирус (ENG)

У The Washington Post вышел интерактивный материал о том, как распространяются инфекции. Основная идея — показать, почему важно ограничивать контакты каждого конкретного человека с внешним миром, а вот закрывать города и страны совсем необязательно. Симуляции показывают, как изменяется кривая количества зараженных в зависимости от того, какая стратегия используется: не делать ничего; попытка закрыть город на карантин; социальная изоляция четверти населения; социальная изоляция 7/8 населения.

Мягкая изоляция выигрывает у карантина, а почти полная изоляция — статистически наиболее надежный способ остановить эпидемию. Симуляции случайные, каждое прочтение статьи даст немного разные результаты, но вывод останется прежним.

Блогер Кевин Симлер улучшил эту модель: он добавил новые вводные (например, инкубационный период и количество умерших от болезни) и параметры модели, которые можно настраивать вручную. Здесь по шагам объясняется, как распространяется вирус и какие переменные на это влияют: например, в одной из симуляций предлагается угадать, какой должна быть скорость передачи заболевания между людьми, чтобы она не успела заразить все население планеты.

Так что это не только подробное пошаговое объяснение того, как распространяется вирус, но еще и упражнение в интуиции и критическом мышлении.

Люди хотят закрытия границ (RUS)

По данным исследования Ipsos по восприятию коронавируса, большинство людей считают, что границы их стран должны быть закрыты до тех пор, пока не будет локализована эпидемия. В опросе приняли участие 12 000 человек из 12 стран. Жители Азиатско-Тихоокеанского региона активнее всех поддерживают идею закрытия границ — во главе с Индией (79%) и Вьетнамом (78%) — что неудивительно, учитывая локацию, в которой болезнь была обнаружена впервые. В Италии 76% также согласны с этой радикальной мерой. Далее следуют Китай (73%) и Россия (70%).

Растет количество человек, которые верят в вероятность заражения людей из их ближнего окружения: их уже больше половины респондентов во Вьетнаме (67%), Великобритании (57%), половина в Индии, Австралии и Японии (51%).

Что ученые знают о 2019-nCoV (RUS)

Сейчас идет разработка лекарств, которые ингибируют заражение на разных стадиях цикла репликации вируса, и вакцин от SARS-CoV/MERS-CoV. Однако пока специфических препаратов от коронавирусов нет, и лечение заключается в поддерживающей терапии, назначенной по состоянию пациента. Источник на 11 марта 2020 года.

Материал обновляется.

Читайте также: