Моделирование эпидемии гриппа в excel

Тип урока: самостоятельная лабораторная работа

Цели:

Теоретические сведения

Вычислительная техника открыла широкие возможности для изучения процессов, происходящих в природе и обществе. Среди задач, успешно моделируемых на компьютерах, особое место занимают экологические, финансовые, биологические и т.д. Круг их очень велик. С одной стороны — это задачи развития биологических видов в природной среде, с другой — исследование влияния деятельности человека на природу. Моделирование в экологической сфере позволяет прогнозировать развитие биологических популяций, управлять численностью отдельных видов и предсказывать влияние угрожающих их развитию факторов.

ЗАДАЧА: Моделирование эпидемии гриппа

Постановка задачи

ФОРМУЛИРОВКА ЗАДАЧИ

Эпидемии всегда представляли серьезную опасность для человечества. На сегодняшний день на Земле эпидемия достигают больших масштабов.

Из-за увеличения коэффициента смертности представляют угрозу для людей различные вирусы гриппа (смертельный грипп В – Брисбен,

Медицина уже давно пришла к выводу о том, что эпидемии лучше предотвращать, а для этого необходимо их изучать и прогнозировать. Применение компьютерного прогнозирования на основе построения математической модели, в данном случае, является наиболее целесообразным решением, так как воспроизведение натуральной эпидемии нежелательно, а модель способна создать реальный эпидемический процесс, не имеющий негативных последствий.

Преимуществом математического моделирования эпидемических процессов является отсутствие больших затрат, быстрота получения результатов, использование вычислительных систем тогда, когда недоступен теоретический подход и др.

ЦЕЛЬ МОДЕЛИРОВАНИЯ

• Составить таблицу данных, характеризующих динамику эпидемии гриппа.
• Построение моделей с различной степенью огрубления природного процесса и принятие решения о целесообразности дальнейшего уточнения модели.
• для прогнозирования характера эпидемического процесса
• для определения стратегии служб здравоохранения.

Информационное моделирование – это творческий процесс. Не существует универсального рецепта построения моделей, пригодного на все случаи жизни, но можно выделить основные этапы и закономерности, характерные для создания самых разных моделей.
Первый этап – постановка задачи. Прежде всего следует уяснить цель моделирования. Исходя из цели моделирования, определяется вид и форма представления информационной модели, а также степень детализации и формализации модели. В соответствии с целью моделирования заранее определяются границы применимости создаваемой модели. На этом этапе также необходимо выбрать инструментарий, который будет использоваться при моделировании (например, компьютерную программу).
Второй этап – собственно моделирование, построение модели. На этом этапе важно правильно выявить составляющие систему объекты, их свойства и взаимоотношения и представить всю эту информацию в уже выбранной форме. Создаваемую модель необходимо периодически подвергать критическому анализу, чтобы своевременно выявлять избыточность, противоречивость и несоответствие целям моделирования.
Третий этап – оценка качества модели, заключающаяся в проверке соответствия модели целям моделирования. Такая проверка может производиться путем логических рассуждений, а также экспериментов, в том числе и компьютерных. При этом могут быть уточнены границы применимости модели. В случае выявления несоответствия модели целям моделирования она подлежит частичной или полной переделке.
Четвертый этап – эксплуатация модели, ее применение для решения практических задач в соответствии с целями моделирования.
Пятый этап – анализ полученных результатов и корректировка исследуемой модели.

Информационная модель

L– всего людей

N_(i)–число больных в i-й день

Z(_i) –число заболевших в i-й день

W_(i) –число выздоровевших за i дней

v_(i) – выздоровевших в i-й день”

Z_(i+1) =k*N_(i) число заболевающих пропорционально числу больных (каждый заражает)

k(i)=a(L-N(i)-W(i)) – к пропорционально числу еще не болевших

при i=0 a=k/(L-N₍₀₎)

КОМПЬЮТЕРНАЯ МОДЕЛЬ

Для моделирования выберем среду табличного процессора. В этой среде информационная модель представляется в виде таблицы, которая содержит две области:

• исходные данные;
• расчетные данные (результаты).

Ход работы:

Задание: провести эксперимент, изменяя коэффициент k и количество больных в начальный момент и сделать выводы.

В тетради записать тему, цель, краткие теоретические сведения, провести эксперимент и слелать вывод(записать в тетради).

Выберите книгу со скидкой:

География на ладони: Краткий курс по устройству планеты

350 руб. 427.00 руб.

ОГЭ. География. Раздел "География России" на ОГЭ

350 руб. 105.00 руб.

ОГЭ. География. Новый полный справочник для подготовки к ОГЭ

350 руб. 242.00 руб.

ЕГЭ-2020. География. Теория и практика

350 руб. 236.00 руб.

ОГЭ. География. Новый полный справочник для подготовки к ОГЭ

350 руб. 171.00 руб.

ОГЭ-2019. География (60х84/8) 10 тренировочных вариантов экзаменационных работ для подготовки к основному государственному экзамену

350 руб. 171.00 руб.

350 руб. 213.00 руб.

350 руб. 231.00 руб.

ЕГЭ. География. Новый полный справочник для подготовки к ЕГЭ

350 руб. 146.00 руб.

350 руб. 127.00 руб.

Атлас + контурные карты 8 класс. География России. Природа и население. ФГОС (с Крымом)

350 руб. 138.00 руб.

Атлас + контурные карты 9 класс. География России. Население, хозяйство и географические районы. ФГОС (с Крымом)

350 руб. 138.00 руб.

БОЛЕЕ 58 000 КНИГ И ШИРОКИЙ ВЫБОР КАНЦТОВАРОВ! ИНФОЛАВКА

• Жмарёв Алексей НиколаевичНаписать 0 28.10.2017

Номер материала: ДБ-797439

Добавляйте авторские материалы и получите призы от Инфоурок

Еженедельный призовой фонд 100 000 Р

Спикер: Анна Быкова (#лениваямама)

29.10.2017 832

29.10.2017 466

29.10.2017 560

28.10.2017 2085

28.10.2017 1492

28.10.2017 550

28.10.2017 576

28.10.2017 767

Не нашли то что искали?

Вам будут интересны эти курсы:

Смоделировать развитие эпидемии гриппа и проанализировать полученные расчётные данные можно, используя технологию обработки числовой информации электронные таблицы Excel. После выполнения практической работы в Excel, на которой изучались вопросы работы с формулами в Excel, относительные и абсолютные ссылки, построение графиков, предлагается продемонстрировать применение полученных знаний и навыков, а также возможностей Excel для рассмотрения конкретной задачи. Закрепление навыков работы на компьютере, применяя методику выполнения конкретных задач с использованием медицинской направленности, позволяет развить у студентов интеллектуальные умения и самостоятельную мыслительную деятельность при работе с информацией.

Моделирование задачи состоит из нескольких этапов: чёткая формулировка задачи, выявления исходных данных для её решения, разработка математической модели решаемой задачи, выбор метода решения, выполнение задачи и анализ полученных результатов.

- количестве заболевших на каждый день,

- количестве нетрудоспособных в связи с болезнью, если допустить, что заболевание длится 10 дней,

- количестве обращений к врачу, если считать, что больной обращается дважды к врачу: в начале заболевания и в конце,

- количестве обращений к врачу,

- количестве врачей для обслуживания больных, если на одного врача допускается двадцать посещений больных.

Построить графики, иллюстрирующие развитие эпидемии гриппа: рост числа заболевших, количество нетрудоспособных в связи с болезнью, число обращений к врачу, зависимость количества врачей, необходимых для обслуживания больных.

- население города 1 млн. человек,

- допустим, в город приехали 20 человек, которые являются переносчиками гриппа.

Для вычисления количества заболевших в определенный день эпидемии используется уравнение:

а =0,000002- коэффициент, характеризующий степень заразности для гриппа,

К1- не перенесшие заболевание (без иммунитета),

К2- заболевшие вчера (они активно продуцируют возбудитель)

III. Практическая часть. Выполнение расчетов. Построение

Для решения поставленной задачи в Excel формируется следующая таблица:

Ещё не перенесли грипп

число обращений к врачу

Количество дней эпидемии целесообразно взять не более 36.

=ОКРУГЛ(0,000002*B2*C2;0); в этой формуле используется округление расчётных данных до целого значения.

Выделив ячейки В3 и С3, можно эти формулы скопировать эти формулы на все дни эпидемии. При таком копировании координаты ячеек в формуле будут относительными, т. е. меняться в зависимости от адреса ячеек, например, в ячейке С4: =ОКРУГЛ(0,000002*B3*C3;0) , а в ячейке В4: =B3-C4 и т. д. После расчёта таблица выглядит так:

Ещё не перенесли грипп

Число обращений к врачу

Таким образом, в каждый последующий день эпидемии расчёт числа заболевших производится относительно данных предыдущего дня эпидемии.

По таблице видно, что пик заболеваемости приходится на 16-ый день эпидемии, и уже к 28-му дню нет вновь заболевших гриппом.

Для расчёта на каждый день заболевших всего необходимо сложить заболевших сегодня и заболевших всего в предыдущий день, для этого в ячейку D3 вводится формула =C3+D2 и затем эта формула копируется в ячейки столбца D на все дни эпидемии. При этом координаты ячеек в формуле будут относительными.

Для вычисления количества нетрудоспособного населения на каждый день эпидемии в связи с болезнью надо учитывать, что заболевание длится 10 дней, поэтому в первые десять дней количество нетрудоспособных в каждый день эпидемии равно числу заболевших сегодня плюс число получивших больничный лист вчера; формула вводится в ячейку E3: =C3+E2 и затем копируется на первые десять дней эпидемии. На 11-ый день эпидемии для расчёта количества нетрудоспособных на каждый день эпидемии надо сложить число заболевших сегодня и число получивших больничный лист вчера, и из полученной суммы вычесть число заболевших в первый день эпидемии, т. к. они уже здоровы. В ячейке E12 вводится формула =C12+E11-C2 и затем копируется на остальные дни эпидемии.

Для расчёта числа обращений к врачу необходимо учесть, что больной обращается дважды к врачу: в начале заболевания и в конце заболевания - на десятый день болезни. Число обращений к врачу первые девять дней эпидемии очевидно равно количеству заболевших сегодня, а на десятый день эпидемии для расчёта числа обращений к врачу к количеству заболевших сегодня прибавляется число заболевших в первый день эпидемии. В ячейку F2 вводится формула =C2, и эта формула копируется на девять дней эпидемии, в ячейку F11 вводится формула =С11+С2 и затем эта формула копируется на все остальные дни эпидемии.

Последний расчёт - количество врачей для обслуживания больных вычисляется в столбике G и равен числу обращений к врачу делить на 20 (по условию задачи на одного врача допускается 20-ть посещений больных за один приём), для этого в ячейку G2 вводится формула =ОКРУГЛ(F2/20;0).

Попытаемся оценить возможный ход эпидемии COVID-19 методом стохастического моделирования. Рассмотрим варианты хода эпидемии без карантина и с различными вариантами карантинных мер.

В единицу времени каждый элемент массива контактирует с другим элементом, выбор координат второго контактирующего проходит с помощью генератора случайных чисел.

Генерация производится по нормальному закону распределения с матожиданием в координатах первого контактирующего и СКО=N/12 для центра массива, с линейно убывающим СКО до N/24 к крайним точкам массива.

Нормальным распределением имитируются более частые контакты с более близкими членами популяции.

Изменение СКО круга контактов имитирует наличие населенных пункты различного размера.

Члены популяции могут иметь пять возможных статусов:

• восприимчивый к вирусу;
• инфицированный на инкубационном периоде;
• больной;
• выздоровевший;
• погибший.

Возможные изменения статусов:

• восприимчивый – инфицированный на инкубационном периоде;
• инфицированный на инкубационном периоде – больной;
• больной – здоровый, либо больной – погибший.

На первом шаге моделирования в центре популяции помещается больной член. При контакте заразного и здорового членов популяции, здоровый член популяции с заданной вероятностью Pз переходит в статус инфицированный на инкубационном периоде, имитация заражения происходит с помощью генератора случайных чисел равномерного распределения.

Заразным считается больной член популяции, либо инфицированный на завершении инкубационного периода.

В каждом случае заражения инкубационный период определяется генератором случайных чисел усеченного нормального распределения, где: Мо-матожидание, СКО=Мо/3, диапазон генератора [1; Mo+10·СКО].

По истечении срока инкубации, генератором случайных чисел, с характеристиками аналогичными генератору срока инкубации, определяется длительность болезни.

По истечении срока болезни, равномерным генератором случайных чисел с заданной вероятностью Рл имитируется выздоровление, либо гибель.

В случае превышения числа больных, нуждающихся в интенсивной терапии, ресурсов системы здравоохранения, случайным образом имитируется гибель больных, необеспеченных ресурсами.

Параметры моделирования COVID-19 на основе открытых источников.

• Средний инкубационный период – 5 дней;
• За 2 суток до проявления симптомов инфицированный становится заразен;
• Cредний срок болезни — 8 суток.
• Летальность Рл=0.5%.

Данное значение принимается на основе следующих данных.

На круизном лайнере Diamond Princess вирусом COVID-19 было заражено 712 человек, 7 человек погибло, летальность составила 0.98%. Diamond Princess единственный случай полного эпидемиологического обследования. Средний возраст пассажиров корабля составлял более 60 лет, для более молодой популяции летальность должна быть ниже.

Как правило, тестирование проводится людям с явными симптомами, поэтому можно предположить, что множество легких и бессимптомных случаев заболевания в статистику не попадает.

Наибольшее число тестов на долю населения проведено в Исландии. На 30 марта в стране зафиксировано 1023 случая заражения COVID-19 и 2 летальных исхода, на 22 марта отмечалось 473 случаев заражения, таким образом летальность 2/473 составляет 0.42%.

Известно, что доля нуждающихся в интенсивной терапии с ИВЛ составляет от 2 до 5%.
С учетом предположения о большом числе незарегистрированных легких случаев, примем для расчетов долю нуждающихся в ИВЛ 1.5% от числа болеющих.

Ресурсы системы здравоохранения, на примере США.

72 тысячи аппаратов ИВЛ, экстренное производство 8 тысяч новых аппаратов. 80000/329000000 доля обеспеченности ИВЛ всей популяции 0.024%.

Результаты моделирования при вероятности заражения Рз=100%

Срок эпидемии от первого зараженного до полного отсутствия болеющих членов популяции и членов на инкубационном периоде – 58 дней.
Пик эпидемии (максимум одновременно болеющих) – 31-й день.
Максимум одновременно болеющих – 50.9% популяции.
Смертность – 10.35% популяции, включая 9.95% из-за нехватки ресурсов интенсивной терапии.
Коллективный иммунитет – 100% популяции (89.65% исходной популяции), затронуто 100% восприимчивых.

В случае близком к идеальному, наблюдаемая по результатам массовых тестирований картина это кумулята числа больных (число зарегистрированных случаев ), в каждый момент времени это число меньше реального общего числа инфицирований на число зараженных на инкубационном периоде.

Стопроцентная заражаемость при контакте предельный случай невозможный в реальной жизни.
Какой может быть реальная вероятность заражаемость?

Рассмотрим два бытовых случая.

В Китае больной коронавирусом заразил 8 человек из 48 находившихся вместе с ним в междугороднем автобусе и одного человека, вошедшего через 30 минут после выхода больного. Вероятность заражения можно оценить 9/49=18.3%.

В Австралии 31 человек из 140 гостей свадьбы заразились COVID-19. Вероятность заражения можно оценить 31/140=22.1%.

Таким образом, примем параметр вероятности заражения Рз=20%.

Результаты моделирования при вероятности заражения Рз=20%

Срок эпидемии от первого зараженного до полного отсутствия болеющих членов популяции и членов на инкубационном периоде – 161 день.
Пик эпидемии (максимум одновременно болеющих) – 73-й день.
Максимум одновременно болеющих – 21.4% популяции.
Смертность – 8.94% популяции, включая 8.56% из-за нехватки ресурсов интенсивной терапии.
Коллективный иммунитет – 94.2% популяции (85.8% исходной популяции), затронуто 94.8% восприимчивых.

Похожие результаты были получены исследователями из Imperial College London, путем более сложного моделирования пик эпидемии ожидается примерно через 2.5 месяца после появления первых зараженных.

Визуализация хода эпидемии на пике заболеваемости:

Цвет ячеек: белый — восприимчивый, желтый — инфицированный на инкубационном периоде, синий — больной, зеленый — выздоровевший, коричневый — погибший.

Репродуктивное число заболеваемости R0

Среднее R0 для Уханя составило 2.2.

В случае Diamond Princess, на котором было заражено около 20%, находившихся на борту, R0 составило 2.8.

При моделировании с Рз=100% репродуктивное число осредняемое за период от начала эпидемии варьируется от 5 до 2.8. Причем значение 2.8 результат по окончанию эпидемии, затронувшей 100% популяции, на момент заражения 20% популяции R0=3.7.

При моделировании с Рз=20% репродуктивное число осредняемое за период от начала эпидемии варьируется от 3 до 1.8. Значение 1.8 определено по окончании эпидемии, затронувшей 100% популяции, на момент заражения 20% популяции R0=2.3.

Таким образом, величина Рз=20% может рассматриваться как репрезентативная.

Результаты моделирования карантинных мер, снижающих вероятности заражения с Рз=20% до 2%

Моделирование начинается с Рз=20%, при достижении эпидемиологического порога 1% больных от состава популяции моделирование продолжается с Рз=2% до полного окончания эпидемии.

Необходимость карантинных мер возникла с 40 дня эпидемии.
Срок эпидемии от первого зараженного до полного отсутствия болеющих членов популяции и членов на инкубационном периоде – 127 дней.
Выздоровление последнего больного после 87 дней непрерывного карантина с Рз=2%.
Пик эпидемии (максимум одновременно болеющих) – 45-й день.
Максимум одновременно болеющих – 2.1% популяции.
Смертность – 0.048% популяции, включая 0.027% из-за нехватки ресурсов интенсивной терапии.
Коллективный иммунитет – 4.33% популяции, затронуто 4.38% восприимчивых, большая вероятность повторной эпидемии.

Результаты моделирования карантинных мер, снижающих вероятности заражения с Рз=20% до 2% сроком на 21 день

Моделирование начинается с Рз=20%, при достижении эпидемиологического порога 1% больных от состава популяции моделирование продолжается с Рз=2% сроком на 21 день, в дальнейшем моделирование легких карантинных мер с Рз=10%.
Необходимость карантинных мер возникла с 39 дня эпидемии.
Срок эпидемии от первого зараженного до полного отсутствия болеющих членов популяции и членов на инкубационном периоде – 749 дней.
На 111 день эпидемии или 51 день после окончания строго карантина с Рз=2% повторное превышение эпидемиологического порога 1% популяции.
Пик эпидемии (максимум одновременно болеющих) – 164-й день.
Максимум одновременно болеющих – 5.8% популяции.
Смертность – 3.52% популяции, включая 3.25% из-за нехватки ресурсов интенсивной терапии.
Коллективный иммунитет – 62.1% популяции (59.9% исходной популяции), затронуто 63.5% восприимчивых.

Результаты моделирования многократных карантинных мер, снижающих вероятности заражения с Рз=20% до 2% сроком на 21 день

Моделирование начинается с Рз=20%, при достижении эпидемиологического порога 1% больных от состава популяции моделирование продолжается с Рз=2% сроком на 21 день, в дальнейшем моделирование легких карантинных мер с Рз=10%, при повторных достижениях эпидемиологического порога 1% моделирование продолжается с Рз=2% сроком на 21 день.
Срок моделирования был ограничен 1000 дней, к окончанию срока эпидемия не была закончена, присутствовало 10 члена популяции на инкубационном периоде и 24 больных.
Необходимость первых карантинных мер возникла с 44 дня эпидемии.
На 114 день эпидемии или 49 день после окончания строго карантина с Рз=2% повторное превышение эпидемиологического порога 1%.
Необходимость 3-6 строгих карантинов с Рз=2% со 197, 286, 370 и 519 дней эпидемии соответственно.
7-й всплеск заболеваемости эпидемиологического порога 1% не превысил.
Пик эпидемии (максимум одновременно болеющих) – 49-й день.
Максимум одновременно болеющих – 1.8% популяции.
Смертность на 1000-й день моделирования – 0.24% популяции, включая 0.01% из-за нехватки ресурсов интенсивной терапии.
Коллективный иммунитет на 1000-й день моделирования – 47.7%, затронуто 48% восприимчивых.

В настоящее время мы наблюдаем, что подавляющее большинстве стран идут по пути карантина. В скором будущем будет понятно какие варианты карантинов выберут лица принимающие государственные решения, по каким путям пойдут, сохранения жизней или минимизации экономических издержек.

Данная статья не подлежит комментированию, поскольку её автор ещё не является полноправным участником сообщества. Вы сможете связаться с автором только после того, как он получит приглашение от кого-либо из участников сообщества. До этого момента его username будет скрыт псевдонимом.

Основные очаги максимально интенсивного распространения заболевания в Китае, Италии, Испании позволяют — по официальным данным — судить о параметрах эпидемии. Так, на 27 марта в Китае число заболевших составило — 81667 чел. В Италии — 80539 чел. В Испании — 57786 чел. В США — 85327 чел. В России сообщается о более, чем 1000 чел.

Очевидно, что приведенные цифры зависят от эффективности и добросовестности институтов официальной статистики, национальной системы здравоохранения и от политических соображений властей той или иной страны по части информационной политики.

Поэтому, следуя выводам работы возможно предположение, что сообщения о 1000 заболевших необходимо умножать на десятки и сотни. Для уточнения российских обстоятельств автором было выполнено моделирование эпидемии коронавируса в России.

Моделирование развития эпидемии может указать на реальные масштабы заболевания, динамики и продолжительности эпидемии.

Отношение читателя к результатам моделирования, как правило, критично. Вплоть до неприятия результатов. Но для специалиста существуют критерии проверки моделирования на достоверность отображения текущего состояния предмета моделирования и прогностичность. Оценить их можно, в частности, по выполнению требования самосогласованности модели (что подтверждает ее адекватность) и ее способности давать приближенные к pеальным показатели.

В данном случае отдельно и независимо друг от друга моделировалось: (1) количество заболевших за каждую неделю, (2) количество умерших и (3) выздоровевших тоже за каждую неделю. Подчеркнем, что каждый из трех показателей моделировался самостоятельно и независимо от двух других. Затем путем суммирования по шкале времени с недельным шагом определялся нарастающий итог указанных трех показателей. Моделирование выполнялось с прогнозом развития эпидемии. В конце подсчитывался баланс. Число всех заболевших за период должно равняться сумме всех умерших и всех выздоровевших. Это требование — проверка на адекватность моделирования. Проверка показала, что баланс при данном моделировании получается с точностью 1%.

Точность официальных данных зависит от соотношения количества проводимых тестов на коронавирус и уровня реальной заболеваемости. По сообщениям российской прессы в конкретных и исключительных известных столичных случаях заболевания ВИП больных (Л.Лещенко, И.Николаев) тест делается за два дня. Из специализированных клиник сообщается, что даже и за 5–7 дней. Это означает пересылку проб в удаленную лабораторию, и, главное, то, что в стране (в регионах) нет сети центров и массового оперативного тестирования на местах. Отсюда следует, что реальный охват потенциально заболевших не может превышать нескольких процентов. Соответственно, официальные данные о числе заболевших нужно увеличивать — для приближения оценки к действительному положению дел, минимум, в десятки раз.

Что касается смертности, то даже официальная статистика говорит о том, что смертность по причине пневмонии (так говорится в графе причина смерти) увеличилась в России по сравнению с предыдущим годом (месяц к месяцу). Увеличение смертности от пневмонии по публикациям в СМИ составляет для сопоставления январь 2020/январь 2019 только в Москве 37%. Официальные лица сообщают из регионов России о росте заболевания пневмонией и смертности от нее уже в феврале 2020 года. Но коронавирус поражает организм больного именно в виде пневмонии! Диагнозы без специального тестирования на коронавирус ставятся попросту неверные. Это подтверждает вышеуказанное предположение, что реальные показатели эпидемии коронавируса в России отличаются от официальных в десятки, а, возможно, что и в сотни раз. Это наносит очевидный ущерб оперативности и масштабу противоэпидемиологических мероприятий.

Для оценки путем специально апробированного моделирования и прогноза российской эпидемии были построены динамики заболеваемости, смертности, выздоровления и итоговый процент смертности больных коронавирусом. Результаты моделирования приведены на рис. 1–2.

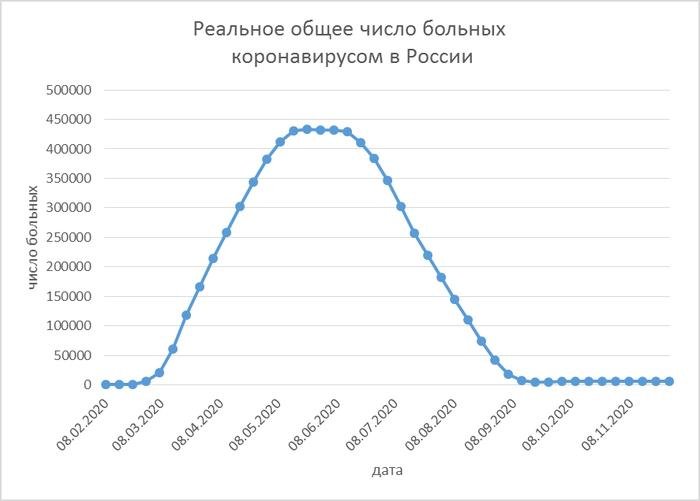
Рис. 1. Оценка динамики реального количества больных коронавирусом в России

Пик текущего количества больных придется на май—июнь 2020 г. Количество заболевших достигнет сотен тысяч человек.

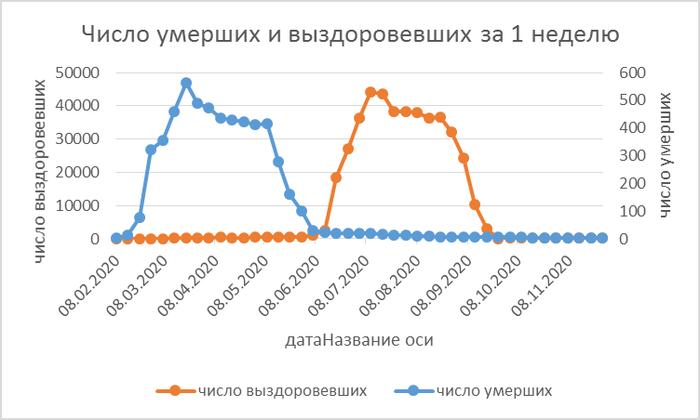
Рис. 2. Оценка скорости (шаг — 1 неделя) реальной смертности и выздоровления больных коронавирусом в России

На рис. 2 видно, что максимальная скорость заболевания пришлась на март, в течение которого серьезных мер по карантину и тестированию, по массовому применению масок и антисептиков, как и специальных порядков поведения людей не предпринималось.

Массовое выздоровление по прогнозу значительно ускорится, начиная с июля. Эпидемия практически прекратится в сентябре 2020 года.

Что следует из проделанного оценочного моделирования?

1. Официальные данные существенно занижены, а представления о динамике развития эпидемии запаздывают, как запаздывают и действия властей. Вместо каникул необходим жесткий карантин. Нужно массированное обеспечение населения и спецперсонала средствами защиты. Нужно массовое развертывание госпиталей. Как это делал Китай.

2. Итоговая смертность от коронавируса в российском случае (по всей длительности эпидемии) при моделировании оценочно составила 1,25%. По всему миру по публикациям в СМИ смертность (на 27 марта 2020 года, то есть текущая, еще до окончания эпидемии) составила — 4,5%. Китай — 4%. Ю.Корея — 1,4%. Япония — 2,3%.

Такое расхождение объясняется следующим. Цифры, которые дают указанные государства, получаются относительно числа заболевших именно коронавирусом, выявленных тестированием. Очевидно, что истинное число заболевших коронавирусом должно быть больше, почему относительная смертность оказывается завышенной. В этой разнице смертность относится на другие диагнозы. Поэтому истинная смертность от коронавируса (которая выявляется при моделировании) должна быть меньше практически наблюдаемой в реальных условиях медицинской практики и государственной информационной политики, о чем говорилось в начале настоящего отчета. В проделанном в данной работе моделировании смертность относится к истинному количеству заболевших коронавирусом.

При моделировании для вышеуказанных стран оценивание смертности дало следующие истинные значения. Для всего мира — 1,44%, Китай — 1,46%, Ю.Корея — 1,4%, Япония — 1,25%.

3. Общее количество умерших в России (именно от коронавируса) моделирование прогнозирует на уровне до 6000 чел. При этом в 2019 году от пневмонии, как таковой, умерло 19000 чел.

4. Вероятно создание и массовое применение вакцины и эффективной терапии заболевания летом (июль) 2020 года. Ожидается эффект летнего температурного влияния на коронавирус.

5. Прогнозируется вторая волна заболеваемости коронавирусом, которая будет существенно более слабой.

6. Полное преодоление эпидемии вероятно осенью (сентябрь) 2020 года. Однако, вероятно, что появится остаточное явление постоянной заболеваемости коронавирусом (эффект спящего вируса) на уровне около 5500 чел при минимальной смертности и при наличии вакцины и лекарств, то есть заболеваемость будет удерживаться на этом уровне применением эффективных методов диагностики и лечения.

Конечно, приведенные материалы будут окончательно проверены на достоверность только по прошествии времени (до конца этого года). Да и то с оговорками относительно достоверности исходных официальных данных. Однако, определенные ориентиры и подсказки специалистам и ответственным государственным структурам для борьбы с эпидемией этот материал, вероятно, наряду с иными модельными прогнозами может дать.

Немаловажно и то, что все, кто ознакомятся с этим материалом, получат определенную информацию для выработки собственных жизненных и гражданских усилий.