Формулы для егэ по математике профильный уровень шпоры
Формулы, правила, свойства. Можно использовать для сдачи ЕГЭ и ОГЭ по математике.
Для начала шпаргалка в компактном виде:
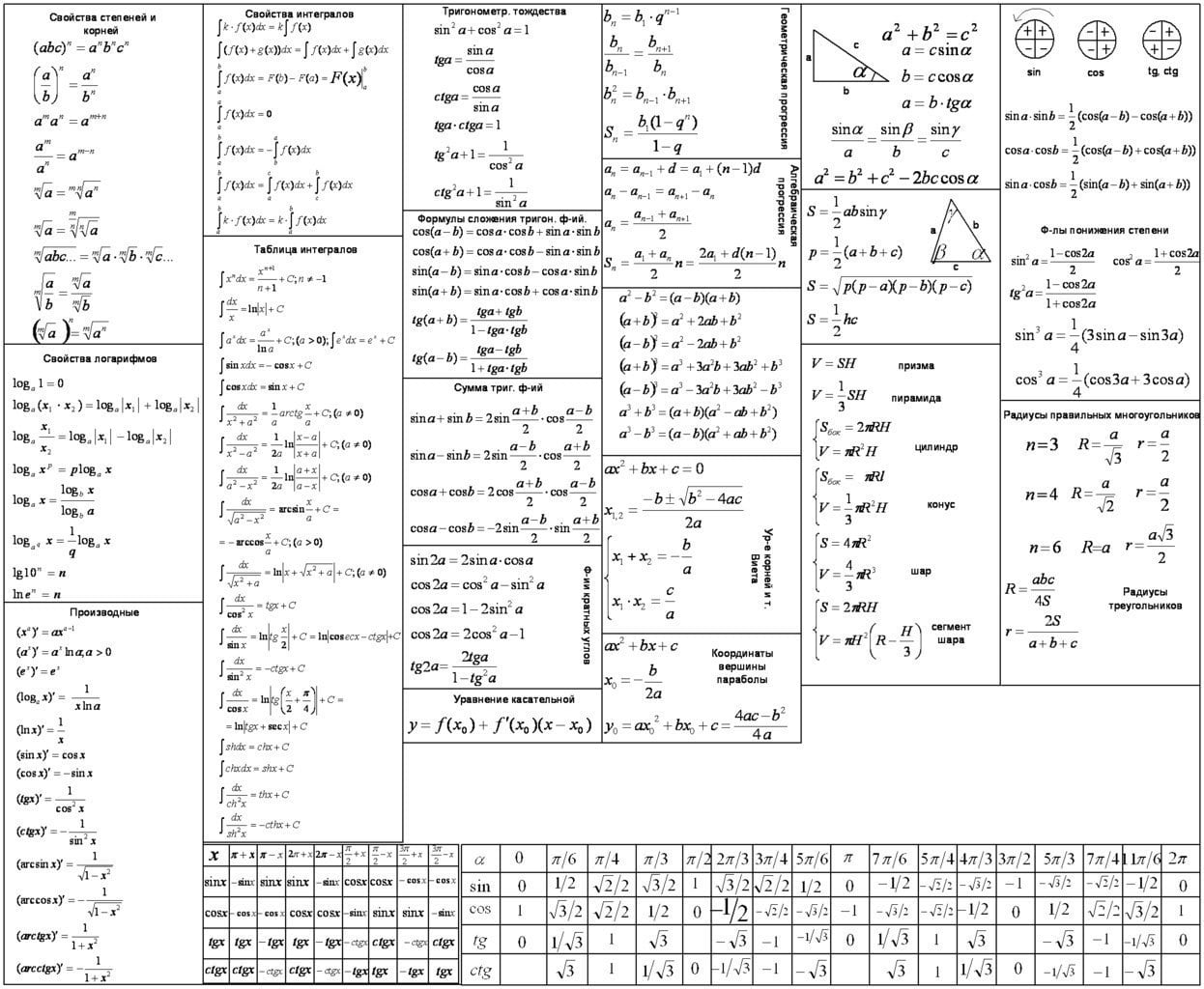
Формулы сокращенного умножения
(а+b) 2 = a 2 + 2ab + b 2
(а-b) 2 = a 2 – 2ab + b 2
a 3 – b 3 = (a-b)( a 2 + ab + b 2 )
a 3 + b 3 = (a+b)( a 2 – ab + b 2 )
(a + b) 3 = a 3 + 3a 2 b+ 3ab 2 + b 3
(a – b) 3 = a 3 – 3a 2 b+ 3ab 2 - b 3
Свойства степеней
a m/n = (a≥0, n ε N, m ε N)
a - r = 1/ a r (a>0, r ε Q)
a m · a n = a m + n
a m : a n = a m – n (a≠0)
Первообразная
Если F’(x) = f(x), то F(x) – первообразная
x n = x n +1 /n+1 + C
a x = a x / ln a + C
cos x = sin x + C
1/ sin 2 x = – ctg x + C
1/ cos 2 x = tg x + C
sin x = – cos x + C
Геометрическая прогрессия
q – знаменатель прогрессии
b n = b1 · q n – 1 – n-ый член прогрессии
Модуль
-a, если a Формулы cos и sin
sin (x + π) = -sin x
cos (x + π) = -cos x
sin (x + 2πk) = sin x
cos (x + 2πk) = cos x
sin (x + π/2) = cos x
Объемы и поверхности тел
1. Призма, прямая или наклонная, параллелепипед V = S·h
2. Прямая призма SБОК = p·h, p – периметр или длина окружности
3. Параллелепипед прямоугольный
V = a·b·c; P = 2(a·b + b·c + c·a)
P – полная поверхность
4. Куб: V = a 3 ; P = 6 a 2
S = 1/3 S·h; S – площадь основания
6. Пирамида правильная S =1/2 p·A
A – апофема правильной пирамиды
7. Цилиндр круговой V = S·h = πr 2 h
8. Цилиндр круговой: SБОК = 2 πrh
9. Конус круговой: V=1/3 Sh = 1/3 πr 2 h
10. Конус круговой: SБОК = 1/2 pL= πrL
Тригонометрические уравнения
sin x = 1, x = π/2 + 2 πn
sin x = -1, x = – π/2 + 2 πn
cos x = 0, x = π/2 + 2 πn
cos x = 1, x = 2πn
cos x = -1, x = π + 2 πn
Теоремы сложения
cos (x +y) = cosx ·cosy – sinx ·siny
cos (x -y) = cosx ·cosy + sinx ·siny
sin (x +y) = sinx ·cosy + cosx ·siny
sin (x -y) = sinx ·cosy – cosx ·siny
tg (x ±y) = tg x ± tg y/ 1 - + tg x ·tg y
ctg (x ±y) = tg x - + tg y/ 1± tg x ·tg y
sin x ± sin y = 2 cos (x±y/2)· cos (x - +y/2)
cos x ± cosy = -2 sin (x±y/2)· sin (x - +y/2)
1 + cos 2x = 2 cos 2 x; cos 2 x = 1+cos2x/2
1 – cos 2x = 2 sin 2 x; sin 2 x = 1- cos2x/2
a,b – основания; h – высота, c – средняя линия S = (a+b/2)·h = c·h
а – сторона, d – диагональ S = a 2 = d 2 /2
a – сторона, d1, d2 – диагонали, α – угол между ними S = d1d2/2 = a 2 sinα
9. Правильный шестиугольник
a – сторона S = (3√3/2)a 2
S = (L/2) r = πr 2 = πd 2 /4
Правила дифференцирования
( f (x) + g (x) )’ = f ’(x) + g’(x)
(tg x)’ = 1/ cos 2 x
(ctg x)’ = – 1/ sin 2 x
(f (kx + m))’ = kf ’(kx + m)
Уравнение касательной к графику функции
Площадь S фигуры, ограниченной прямыми x = a , x = b
Формула Ньютона-Лебница
| t | π/4 | π/2 | 3π/4 | π |
| cos | √2/2 | 0 | -√2/2 | 1 |
| sin | √2/2 | 1 | √2/2 | 0 |
| t | 5π/4 | 3π/2 | 7π/4 | 2π |
| cos | -√2/2 | 0 | √2/2 | 1 |
| sin | -√2/2 | -1 | -√2/2 | 0 |
| t | 0 | π/6 | π/4 | π/3 |
| tg | 0 | √3/3 | 1 | √3 |
| ctg | - | √3 | 1 | √3/3 |
sin x = b x = (-1) n arcsin b + πn
cos x = b x = ± arcos b + 2 πn
tg x = b x = arctg b + πn
ctg x = b x = arcctg b + πn
Теорема синусов : a/sin α = b/sin β = c/sin γ = 2R
Теорема косинусов : с 2 =a 2 +b 2 -2ab cos y
Неопределенные интегралы
∫ x n dx = (x n +1 /n+1) + C
∫ sin x dx = – cos x + C
∫ cos x dx = sin x + C
∫ dx/sin 2 x = -ctg + C
∫ dx/cos 2 x = tg + C
∫ x r dx = x r+1 /r+1 + C
Логарифмы
| Градус | 0 | 30 | 45 | 60 |
| sin | 0 | 1/2 | √2/2 | √3/2 |
| cos | 1 | √3/2 | √2/2 | 1/2 |
| tg | 0 | √3/3 | 1 | √3 |
| t | π/6 | π/3 | 2π/3 | 5π/6 |
| cos | √3/2 | 1/2 | -1/2 | -√3/2 |
| sin | 1/2 | √3/2 | √3/2 | 1/2 |
| 90 | 120 | 135 | 150 | 180 |
| 1 | √3/2 | √2/2 | 1/2 | 0 |
| 0 | -1/2 | -√2/2 | -√3/2 | -1 |
| - | -√3 | -1 | √3/3 | 0 |
| t | 7π/6 | 4π/3 | 5π/3 | 11π/6 |
| cos | -√3/2 | -1/2 | 1/2 | √3/2 |
| sin | -1/2 | -√3/2 | -√3/2 | -1/2 |
Формулы двойного аргумента
cos 2x = cos 2 x – sin 2 x = 2 cos 2 x -1 = 1 – 2 sin 2 x = 1 – tg 2 x/1 + tg 2 x
sin 2x = 2 sin x · cos x = 2 tg x/ 1 + tg 2 x
tg 2x = 2 tg x/ 1 – tg 2 x
ctg 2x = ctg 2 x – 1/ 2 ctg x
sin 3x = 3 sin x – 4 sin 3 x
cos 3x = 4 cos 3 x – 3 cos x
tg 3x = 3 tg x – tg 3 x / 1 – 3 tg 2 x
sin s cos t = (sin (s+t) + sin (s+t))/2
sin s sin t = (cos (s-t) – cos (s+t))/2
cos s cos t = (cos (s+t) + cos (s-t))/2
Формулы дифференцирования
x’ = 1 (sin x)’ = cos x
(kx + m)’ = k (cos x)’ = – sin x
(1/x)’ = – (1/x 2 ) ( ln x)’ = 1/x
(e x )’ = e x ; (x n )’ = nx n-1 ;(log a x)’=1/x ln a
Площади плоских фигур
1. Прямоугольный треугольник
S = 1/2 a·b (a, b – катеты)
2. Равнобедренный треугольник
S = (a/2)·√ b 2 – a 2 /4
3. Равносторонний треугольник
S = (a 2 /4)·√3 (a – сторона)
4. Произвольный треугольник
a,b,c – стороны, a – основание, h – высота, A,B,C – углы, лежащие против сторон; p = (a+b+c)/2
S = 1/2 a·h = 1/2 a 2 b sin C =
a 2 sinB sinC/2 sin A= √p(p-a)(p-b)(p-c)
a,b – стороны, α – один из углов; h – высота S = a·h = a·b·sin α
cos (x + π/2) = -sin x
Формулы tg и ctg
tg x = sin x/ cos x; ctg x = cos x/sin x
ctg (x + πk) = ctg x
ctg (x ± π) = ± ctg x
tg (x + π/2) = – ctg x
ctg (x + π/2) = – tg x
sin 2 x + cos 2 x =1
1 + tg 2 x = 1/ cos 2 x
1 + ctg 2 x = 1/ sin 2 x
tg 2 (x/2) = 1 – cos x/ 1 + cos x
cos 2 (x/2) = 1 + cos x/ 2
sin 2 (x/2) = 1 – cos x/ 2
P = 4 πR 2 = πD 2
V = πh 2 (R-1/3h) = πh/6(h 2 + 3r 2 )
SБОК = 2 πRh = π(r 2 + h 2 ); P= π(2r 2 + h 2 )
V = 1/6 πh 3 + 1/2 π(r 2 + h 2 )· h;
14. Шаровой сектор:
V = 2/3 πR 2 h’ где h’ – высота сегмента, содержащего в секторе
Формула корней квадратного уравнения
ax 2 + bx + c = 0 (a≠0)
Если D=0, то x = -b/2a (D = b 2 -4ac)
Если D>0, то x1,2 = -b± /2a
Арифметическая прогрессия
a n+1 = a n + d, где n – натуральное число
d – разность прогрессии;
a n = a 1 + (n – 1)·d – формула n-го члена
Радиус описанной окружности около многоугольника
R = a/ 2 sin 180/n
Радиус вписанной окружности
L = 2 πR S = πR 2
Площадь конуса
Тангенс угла - отношение противолежащего катета к прилещащему. Котангенс – наоборот.
Скачать шпаргалки по математике
Скачать всё это в компактном виде: matematika-shpory.doc.
Рекомендуем:
- Математика
- Русский язык
- Обществознание
- Физика
- Биология
- География
- Иностранные языки
- Информатика
- Литература
- Химия
- История
- Математика
- Русский язык
- Обществознание
- Физика
- Биология
- География
- Иностранные языки
- Информатика
- Литература
- Химия
- История
- Математика
- Русский язык
- Обществознание
- Физика
- Биология
- География
- Иностранные языки
- Информатика
- Литература
- Химия
- История
- Математика
- Русский язык
- Обществознание
- Физика
- Биология
- География
- Иностранные языки
- Информатика
- Литература
- Химия
- История
- Инструкция абитуриента от EGEIGIA.RU
- Календарь абитуриента 2015 - даты и сроки
- Навигатор абитуриента
- Выбираем специальность
- Зарплаты по профессиям
- Инструкция по поступлению в ВУЗ
- Калькулятор баллов ЕГЭ – выбираем вуз
- Проходные баллы ЕГЭ при поступлении
- Как стать студентом
- Как подавать документы в ВУЗ
- Готовиться ли к ЕГЭ в 10 классе?
- Как готовиться к ЕГЭ? Как готовиться к ГИА?
- Советы психолога
- Советы психолога родителям
- Зачем мне статистика?
- Оценки за ГИА
- Cпособ подготовки к ОГЭ 2015 по математике (ГИА 9)
- Открытый банк заданий ФИПИ сохраняем в PDF
Как готовиться к ГИА? Часто этот вопрос становится серьёзной проблемой для школьника и родителей. Выбрать ли репетитора, найти курсы, или есть другой способ? .

Бесплатные видео уроки ЕГЭ 2018 по математике профильного уровня. Можно использовать для домашней подготовки или учителем для работы в классе .

Видео уроки ЕГЭ 2018 по математике базовый уровень. Обучение всем приемам решения. Можно использовать для домашней подготовки или учителем для работы в классе .

Бесплатные видео уроки ОГЭ 2018 по математике (ГИА-9). Обучение всем приемам решения. Можно использовать для домашней подготовки или учителем для работы в классе .

Как подсчитывают результаты ЕГЭ? Как оцениваются ваши знания; что такое шкалирование; первичные и тестовые баллы? Давайте разберемся! .
Формулы по математике для подготовки к ЕГЭ – шпаргалка
- 1
- 2
- 3
- 4
- 5
Подробности Категория: Теория и практика к заданиям

В этой подборке формул использованы 3 основных принципа, для упрощения запоминания:
- Выбраны только те формулы, которые могут встретиться на ЕГЭ по математике (это лишь часть того, что изучено в школе);
- Формулы разобраны на тематические блоки;
- Блоки формул выделены цветовым фоном, который позволяет, всего после нескольких обращений, вспоминать картинку и буквально читать с нее нужную формулу.
Как легко запомнить именно нужные формулы из всего курса математики?
Для подготовки нужно выбрать такое оформление математических формул, чтобы они отложились в памятки наиболее эффективно.
Шпаргалки по математике, алгебре и геометрии Шпаргалки по физике / Шпаргалки по химии
| Таблица квадратов. Таблица степеней. Формулы сокращенного умножения. Модуль числа. Свойства модуля: | Уравнения и неравенства с модулем. Последовательности и прогрессии. Метод кординат на плоскости. Скалярное произведение векторов. Расстояние между точками. | Тригонометрия - основные формулы. Таблица значений тригонометрических функций. Решение тригонометрических уравнений: | Четность и нечетность тригонометрических функций. Обратные тригонометрические функции. Формулы приведения. Знаки тригонометрических функций. Показательные уравнения и неравенства. |
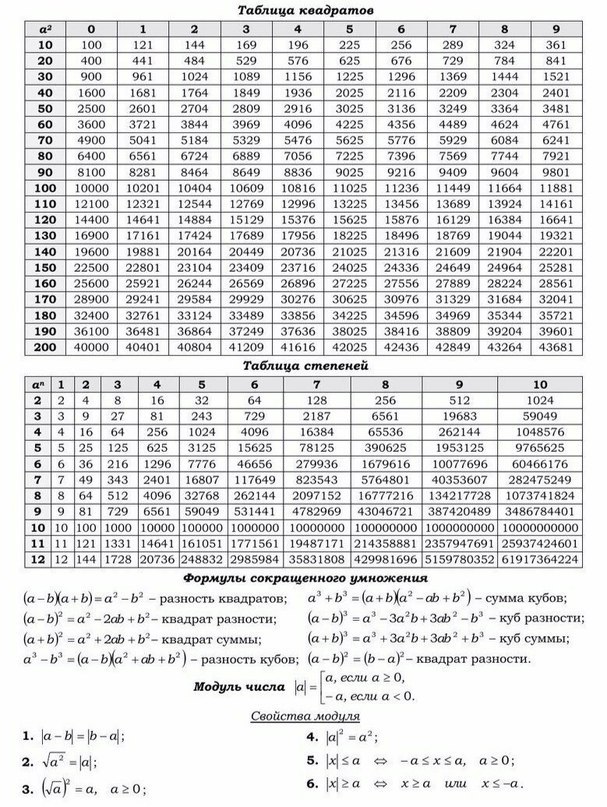 |  | 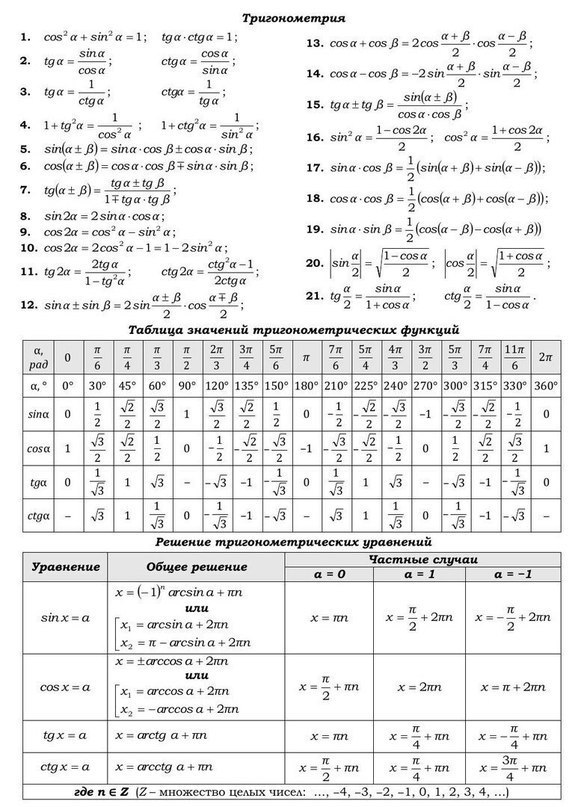 |  |
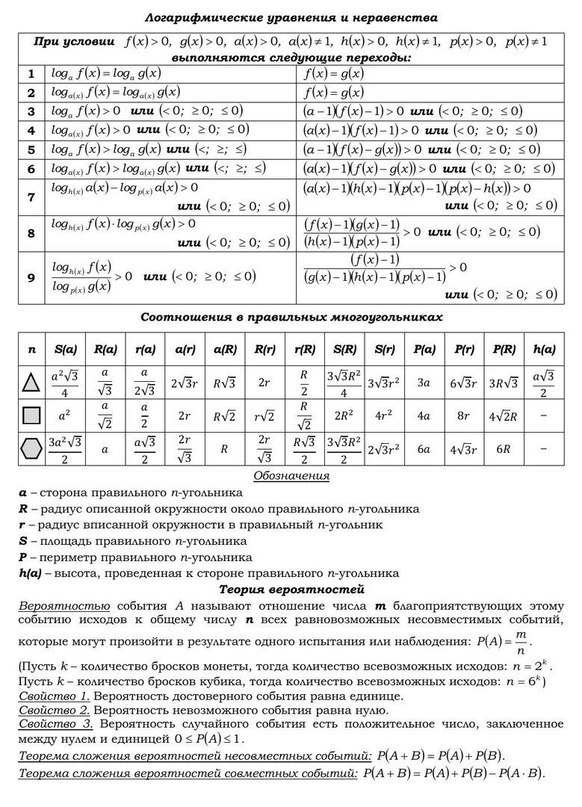
| Корень n-ой степени. Степени. Иррациональные уравнения и неравенства. Логарифм, свойства логарифмов | Логарифмические уравнения и неравенства. Соотношения в правильных многоугольниках. Теория вероятностей. Теоремы сложения вероятностей. | Логарифмические уравнения и неравенства. | Производная. Правила дифференцирования. Производная сложной функции. Уравнение касательной к графику функции в точке. |
 |  |  |  |
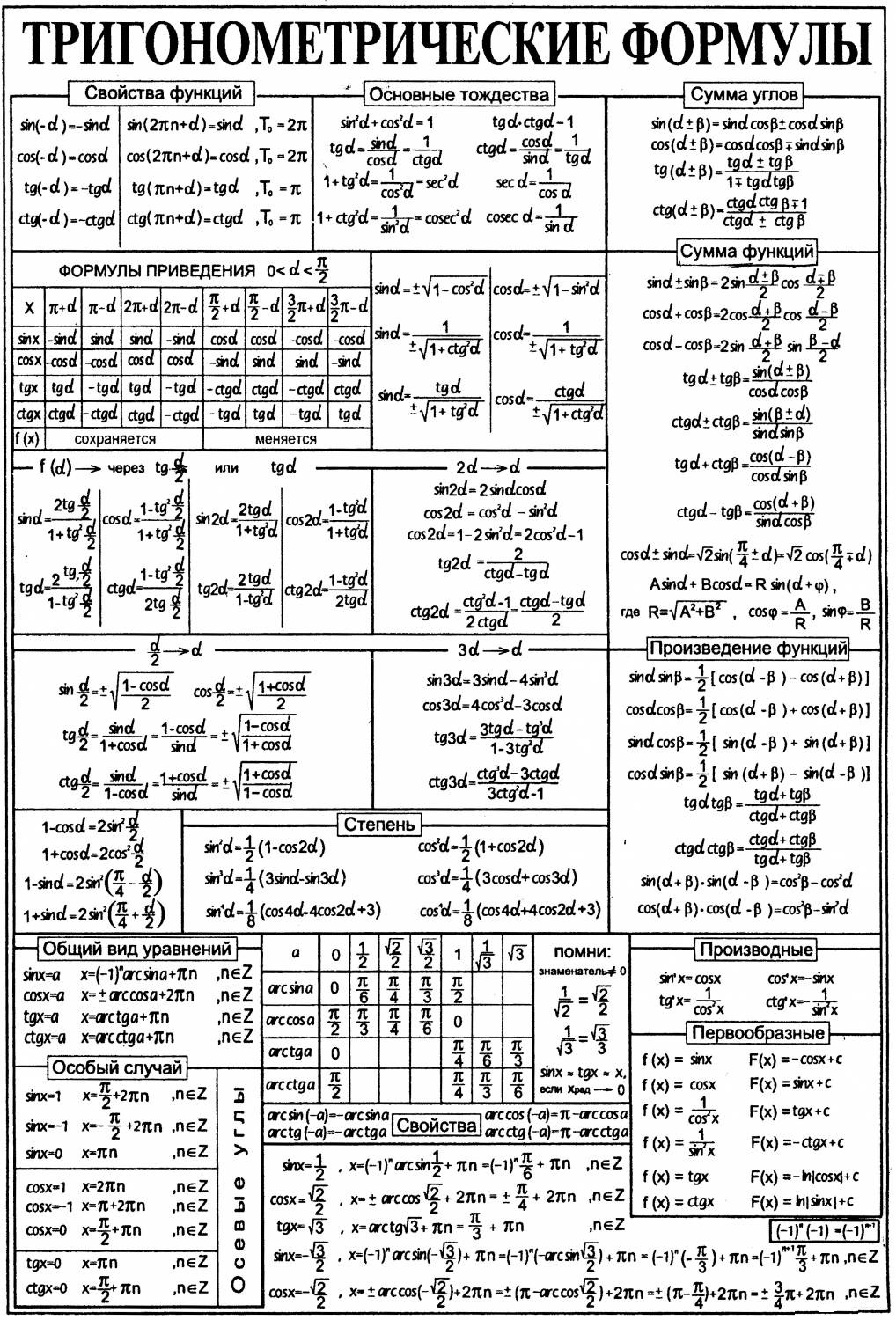
| Тригонометрические формулы. Свойства функций, основные тождества, сумма углов. Сумма функций, формулы приведения, особые случаи, степени, половинные, двойные и тройные углы. Обратные функции. | |||
 |
| Набор 2 - Алгебра. Линейная алгебра. | |||
| Свойства степеней. Формулы сокращенного умножения. Свойства арифметических корней. Модуль. Начала математического анализа: прогрессии арифметическая и геометрическая. Производная. Первообразная и интеграл. Среднее арифметическое и среднее геометрическое. | Тригонометрия. Основные формулы. Арксинус, арккосинус, арктангенс, арккотангенс. Четность функций. Значения тригонометрических функций некоторых углов. | Графики некоторых элементарных функций. Логарифмы. Решение квадратных, иррациональных, показательных, тригонометрических уравнений, уравнений с модулем | Квадратные неравенства. Неравенства с модулем. Логарифмические неравенства. Неравенства с модулем. Иррациональные неравенства. Показательные неравенства. Комбинаторика и бином Ньютона. |
 |  |  |  |
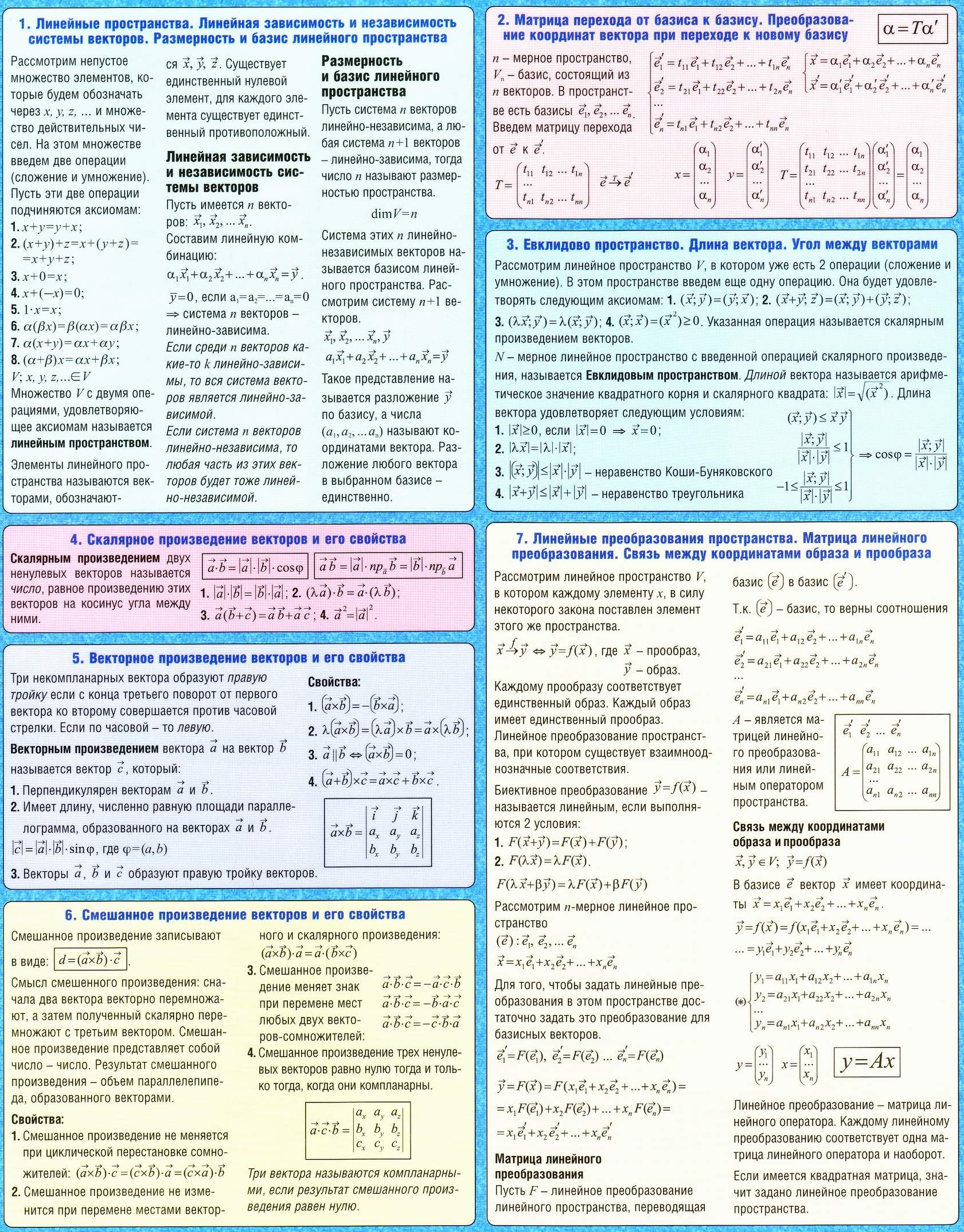
| Определение комплексного числа. Геометрическая интерпретация комплексного числа. Тригонометрическая форма комплексного числа. Показательная форма комплексного числа. Действия с комплексными числами. Последовательности, пределы последовательности. Теоремы о пределах числовых последовательностей. | Определение предела числовой функции. Односторонние пределы. Свойства пределов. Непрерывные функции и их свойства. Точки разрыва и их классификации. Замечательные пределы. Важные пределы. Теоремы о среднем. Правило Лопиталя. | Линейные пространства. Линейная зависимость и независимость системы векторов. Размерность и базис линейного пространства. Скалярное и векторное произведение векторов. Смешанное произведение векторов. Матрица перехода от базиса к базису. Преобразование координат вектора при переходе к новому базису. Евклидово пространство. Длина вектора. Угол между векторами. Линейные преобразования пространства. Матрица линейного преобразования. Связь между координатами образа и прообраза. | Связь между координатами одного и того же линейного оператора в разных базисах. Угол между прямой и плоскостью. Расстояние от точки до плоскости. Характеристические уравнения линейного оператора. Собственные векторы линейного оператора и их свтойства. Поверхности второго порядка. Плоскость в пространстве. Виды углов в пространстве. Уравнения плоскости. |
 |  |  |  |
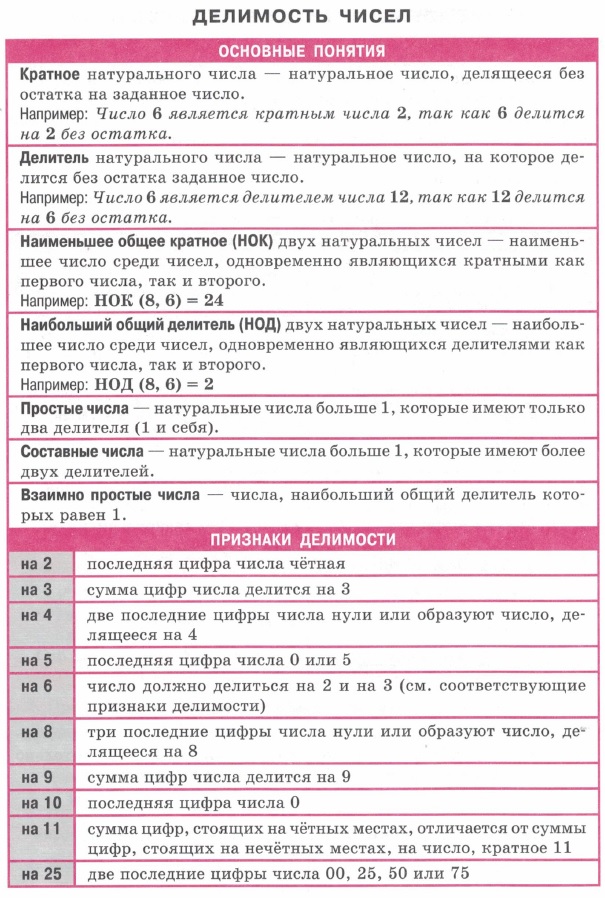
| Делимость чисел. Кратное. Делитель. НОК. НОД Простые и составные числа. Взаимно простые числа. | Числовые последовательности, члены, способы задания. Арифметическая и геометрическая прогрессии. Формулы. Характеристические свойства | Числа. Множества натуральных, целых, рациональных, действительных, иррациональных чисел. Арифметические действия с дробями. Модуль - свойства. | Решение квадратных уравнений. Формулы дискриминанта. Решение неполных квадратных уравнений. Теорема Виета. Алгоритм решения квадратного неравенства. |
 |  |  |  |
| Основные свойства функций. Понятие функции. Четность и нечетность. Периодичность. Нули функции. Промежутки знакопостоянства. Монотонность (возрастание, убывание). Асимптоты. Алгоритм описания фукнкции. |
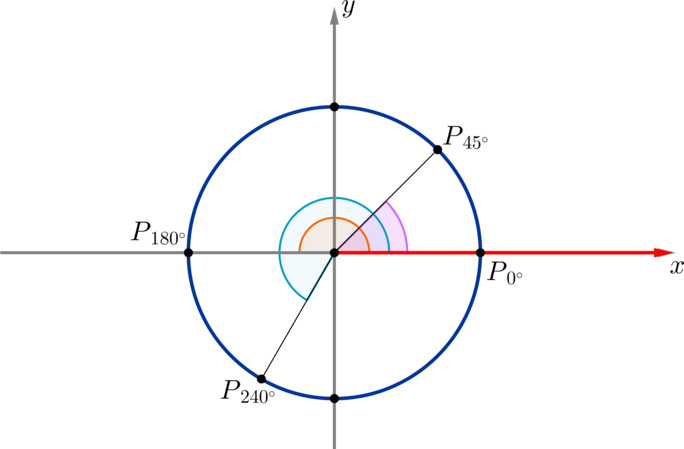
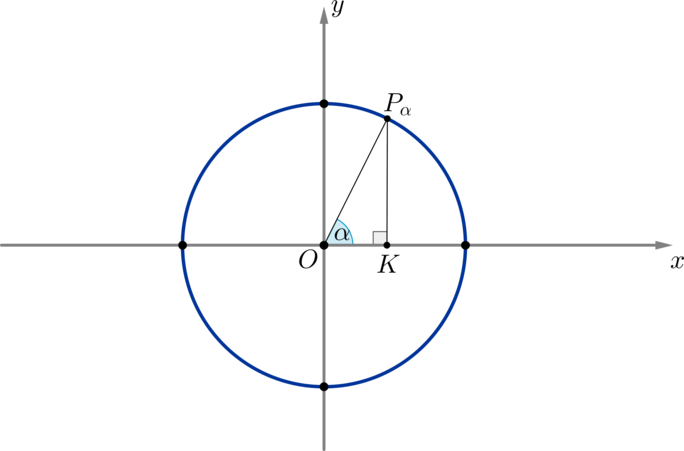
Преобразование графиков функций у= f(x) в y=-f(x); y=f(-x); y=-f(-x); y=f(x-a); y=f(x)+b; y=f(ax); y=kf(x); y=|f(x)|; y=f(|x|). Построение графика обратной функции Степенные функции y=xn и y=x1/n, n∈Z. Свойства, графики. Квадратичная функция. Свойства степеней. Свойства арифметических корней. Формулы сокращенного умножения. Примеры значения степенных функций. Неравенства, понятия, строгие, нестрогие, решение. Свойства неравенств. Решение линейных неравенств. Решение квадратных неравенств. Метод интервалов при решении неравенств. Решение показательных неравенств. Решение логарифмическмх неравенств. Решение иррациональных неравенств. Решение неравенств с модулем. Часто применяемые неравенства Интегрирование функций. Понятие и основное свойство первообразной. Неопределенный интеграл. Правила интегрирования. Определенный интеграл. Формула Ньютона-Лейбница. Свойства и геометрический смысл определенного интеграла. Физический смысл определенного интеграла Уравнения прямой на плоскости. Общее уравнение прямой. Уравнение прямой "в отрезках". Уравнение прямой с угловым коэффициентом. Уравнение пучка прямых, проходящих через точку. Уравнение прямой, проходящей через 2 точки. Нормальное уранение прямой. Консультации и техническая \(\blacktriangleright\) Рассмотрим прямоугольную систему координат и в ней окружность с единичным радиусом и центром в начале координат. Угол в \(1^\circ\) — это такой центральный угол, который опирается на дугу, длина которой равна \(\dfrac1<360>\) длины всей окружности. \(\blacktriangleright\) Будем рассматривать на окружности такие углы, у которых вершина находится в центре окружности, а одна сторона всегда совпадает с положительным направлением оси \(Ox\) (на рисунке выделено красным).
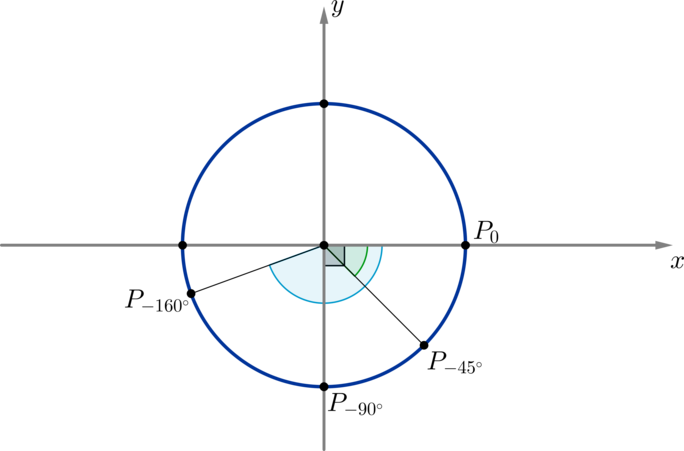
Точку, в которой вторая сторона такого угла \(\alpha\) пересекает окружность, будет называть \(P_<\alpha>\) . Таким образом, можно сказать, что мы совершаем поворот по окружности из начального положения \(P_0\) до положения \(P_<\alpha>\) на угол \(\alpha\) . \(\blacktriangleright\) Поворот по окружности против часовой стрелки — это поворот на положительный угол. Поворот по часовой стрелке — это поворот на отрицательный угол. Например, на рисунке отмечены углы \(-45^\circ, -90^\circ, -160^\circ\) :
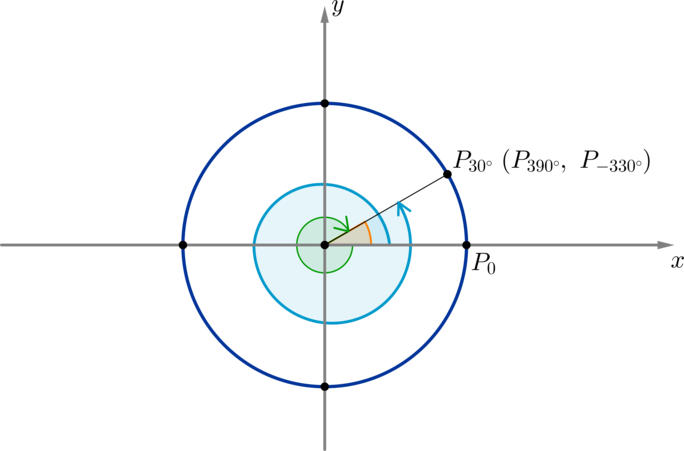
\(\blacktriangleright\) Рассмотрим точку \(P_<30^\circ>\) на окружности. Для того, чтобы совершить поворот по окружности из начального положения до точки \(P_<30^\circ>\) , необходимо совершить поворот на угол \(30^\circ\) (оранжевый). Если мы совершим полный оборот (то есть на \(360^\circ\) ) и еще поворот на \(30^\circ\) , то мы снова попадем в эту точку, хотя уже был совершен поворот на угол \(390^\circ=360^\circ+30^\circ\) (голубой). Также попасть в эту точку мы можем, совершив поворот на \(-330^\circ\) (зеленый), на \(750^\circ=360^\circ+360^\circ+30^\circ\) и т.д.
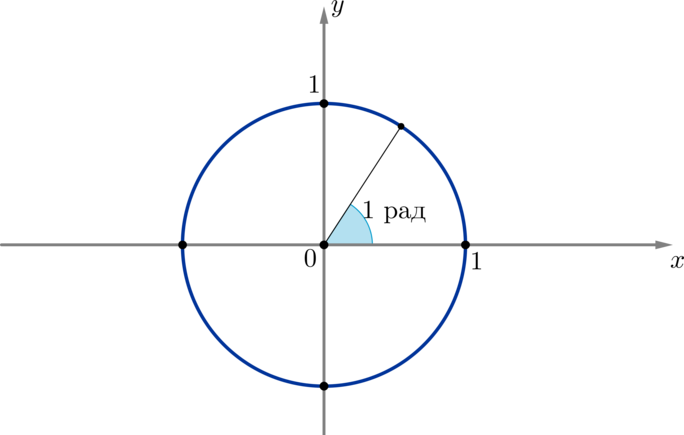
Все углы, находящиеся в точке \(P_<30^\circ>\) можно записать в виде: \(\alpha=30^\circ+n\cdot 360^\circ, \ n\in\mathbb \(\blacktriangleright\) Угол в \(1\) радиан — это такой центральный угол, который опирается на дугу, длина которой равна радиусу окружности: Т.к. длина всей окружности радиусом \(R\) равна \(2\pi R\) , а в градусной мере — \(360^\circ\) , то имеем \(360^\circ=2\pi \cdot 1\textbf< рад>\) , откуда \[180^\circ=\pi \textbf< рад>\] Это основная формула, с помощью которой можно переводить градусы в радианы и наоборот. Пример 1. Найти радианную меру угла \(60^\circ\) . Т.к. \(180^\circ = \pi \Rightarrow 1^\circ = \dfrac<\pi> <180>\Rightarrow 60^\circ=\dfrac<\pi>3\) Пример 2. Найти градусную меру угла \(\dfrac34 \pi\) . Т.к. \(\pi=180^\circ \Rightarrow \dfrac34 \pi=\dfrac34 \cdot 180^\circ=135^\circ\) . Обычно пишут, например, не \(\dfrac<\pi>4 \text< рад>\) , а просто \(\dfrac<\pi>4\) (т.е. единицу измерения “рад” опускают). Обратим внимание, что обозначение градуса при записи угла не опускают. Таким образом, под записью “угол равен \(1\) ” понимают, что “угол равен \(1\) радиану”, а не “угол равен \(1\) градусу”. Т.к. \(\pi \thickapprox 3,14 \Rightarrow 180^\circ \thickapprox 3,14 \textbf < рад>\Rightarrow 1 \textbf < рад>\thickapprox 57^\circ\) . \(\blacktriangleright\) Из курса планиметрии (геометрии на плоскости) мы знаем, что для углов \(0 определены синус, косинус, тангенс и котангенс следующим образом:
Т.к. на единичной окружности определены любые углы \(\alpha\in(-\infty;+\infty)\) , то нужно определить синус, косинус, тангенс и котангенс для любого угла.
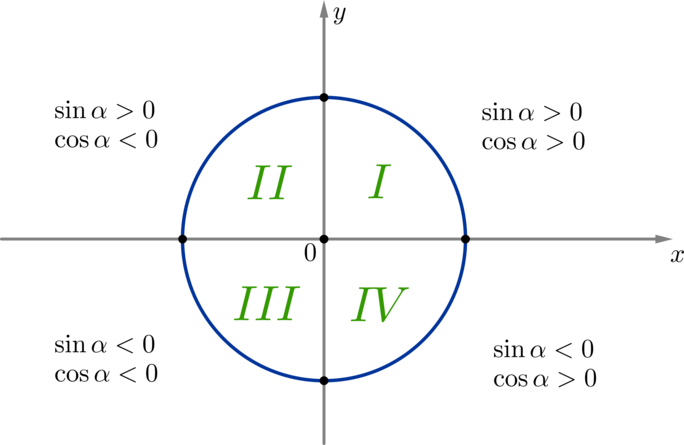
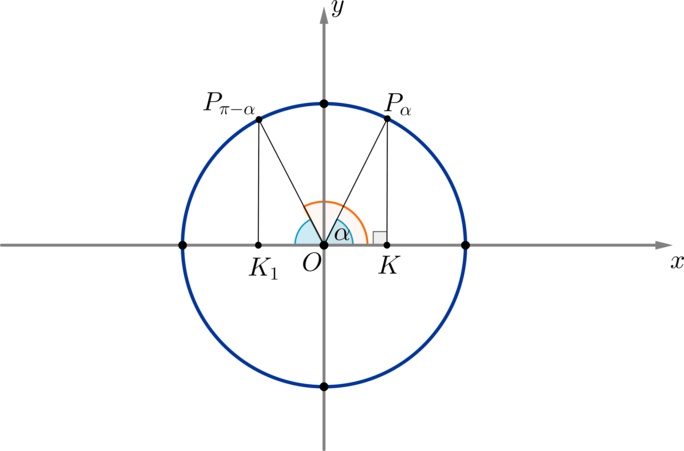
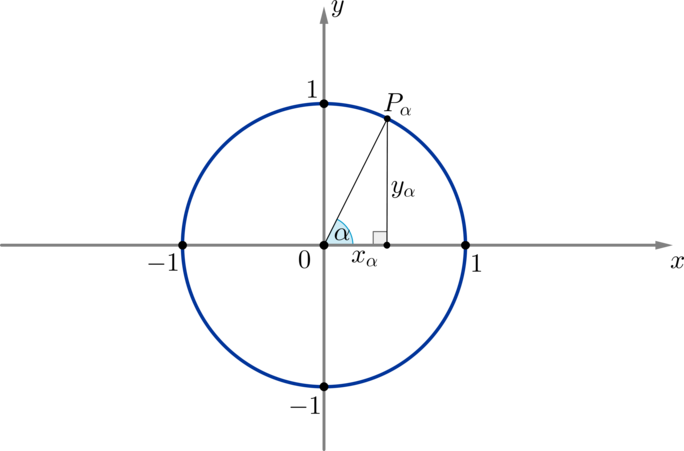
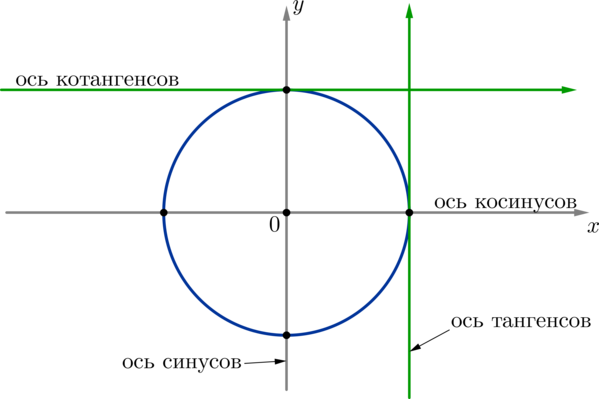
Опустим перпендикуляр \(P_<\alpha>K\) из точки \(P_<\alpha>\) на ось \(Ox\) . Мы получим прямоугольный треугольник \(\triangle OP_<\alpha>K\) , из которого имеем: \[\sin\alpha=\dfrac Таким образом, если точка \(P_<\alpha>\) имела координаты \((x_<\alpha>\,;y_<\alpha>)\) , то через соответствующий ей угол ее координаты можно переписать как \((\cos\alpha\,;\sin\alpha)\) . Определение: 1. Синусом угла \(\alpha\) называется ордината точки \(P_<\alpha>\) , соответствующей этому углу, на единичной окружности. 2. Косинусом угла \(\alpha\) называется абсцисса точки \(P_<\alpha>\) , соответствующей этому углу, на единичной окружности. Поэтому ось \(Oy\) называют осью синусов, ось \(Ox\) — осью косинусов. \(\blacktriangleright\) Окружность можно разбить на \(4\) четверти, как показано на рисунке. Пример 3. Так как, например, точки \(P_<\frac<\pi><6>>\) и \(P_<-\frac<11\pi>6>\) совпадают, то их координаты равны, т.е. \(\sin\dfrac<\pi>6=\sin \left(-\dfrac<11\pi>6\right),\ \cos \dfrac<\pi>6=\cos \left(-\dfrac<11\pi>6\right)\) . Пример 4. Рассмотрим точки \(P_<\alpha>\) и \(P_<\pi-\alpha>\) . Пусть для удобства \(0 .
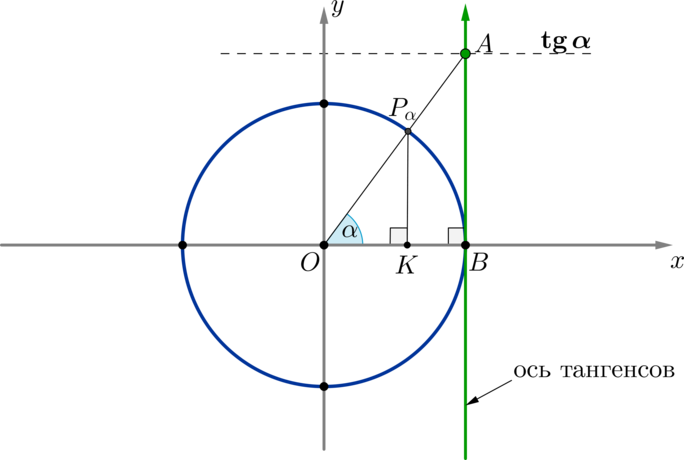
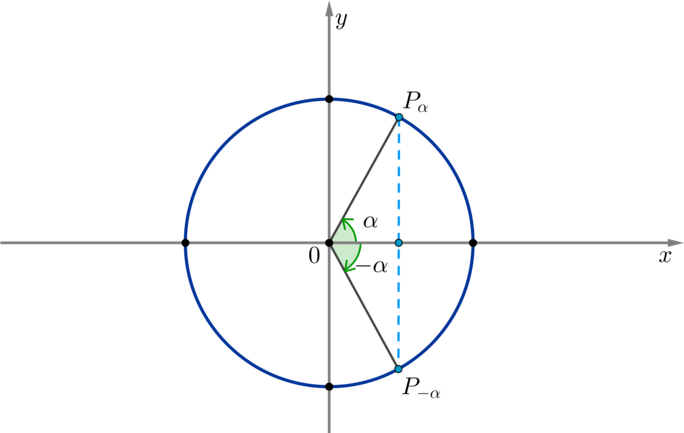
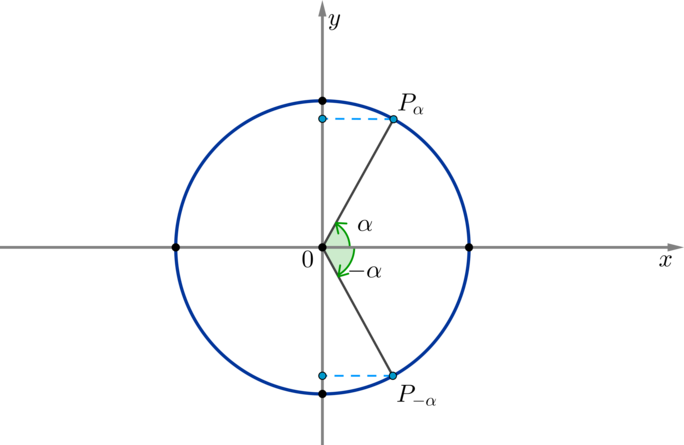
Таким образом доказываются и другие формулы, называемые формулами приведения: \[<\large<\begin С помощью этих формул можно найти синус или косинус любого угла, сведя это значение к синусу или косинусу угла из \(I\) четверти. Таблица синусов, косинусов, тангенсов и котангенсов углов из первой четверти: Заметим, что данные значения были выведены в разделе “Геометрия на плоскости (планиметрия). Часть II” в теме “Начальные сведения о синусе, косинусе, тангенсе и котангенсе”. Пример 5. Найдите \(\sin<\dfrac<3\pi>4>\) . \(\blacktriangleright\) Для упрощения запоминания и использования формул приведения можно следовать следующему правилу. Случай 1. Если угол можно представить в виде \(n\cdot \pi\pm \alpha\) , где \(n\in\mathbb Знак угла можно найти, определив, в какой четверти он находится. Пользуясь таким правилом, предполагаем, что угол \(\alpha\) находится в \(I\) четверти. Случай 2. Если угол можно представить в виде \(n\cdot \pi+\dfrac<\pi>2\pm\alpha\) , где \(n\in\mathbb Знак определяется таким же образом, как и в случае \(1\) . Заметим, что в первом случае функция остается неизменной, а во втором случае — меняется (говорят, что функция меняется на кофункцию). Пример 6. Найти \(\sin \dfrac<13\pi><3>\) . Преобразуем угол: \(\dfrac<13\pi><3>=\dfrac<12\pi+\pi><3>=4\pi+\dfrac<\pi>3\) , следовательно, \(\sin \dfrac<13\pi><3>=\sin \left(4\pi+\dfrac<\pi>3\right)=\sin\dfrac<\pi>3=\dfrac<\sqrt3>2\) Пример 7. Найти \(\cos \dfrac<17\pi><6>\) . Преобразуем угол: \(\dfrac<17\pi><6>=\dfrac<18\pi-\pi><6>=3\pi-\dfrac<\pi>6\) , следовательно, \(\cos \dfrac<17\pi><6>=\cos \left(3\pi-\dfrac<\pi>6\right)=-\cos\dfrac<\pi>6=-\dfrac<\sqrt3>2\) \(\blacktriangleright\) Область значений синуса и косинуса. \(\blacktriangleright\) Тангенс и котангенс. 1) \(<\large<\mathrm 2) тангенс и котангенс положительны в \(I\) и \(III\) четвертях и отрицательны в \(II\) и \(IV\) четвертях. 3) область значений тангенса и котангенса — все вещественные числа, т.е. \(\mathrm 4) для тангенса и котангенса также определены формулы приведения. Случай 1. Если угол можно представить в виде \(n\cdot \pi\pm \alpha\) , где \(n\in\mathbb Случай 2. Если угол можно представить в виде \(n\cdot \pi+\dfrac<\pi>2\pm\alpha\) , где \(n\in\mathbb 5) ось тангенсов проходит через точку \((1;0)\) параллельно оси синусов, причем положительное направление оси тангенсов совпадает с положительным направлением оси синусов; \(\triangle OP_<\alpha>K \sim \triangle AOB \Rightarrow \dfrac Таким образом, если точку \(P_<\alpha>\) соединить прямой с центром окружности, то эта прямая пересечет линию тангенсов в точке, значение которой равно \(\mathrm 6) из основного тригонометрического тождества вытекают следующие формулы: \[1+\mathrm Обращаем внимание, что тангенс не определен в углах, где косинус равен нулю (это \(\alpha=\dfrac<\pi>2+\pi n, n\in\mathbb \(\blacktriangleright\) Четность косинуса и нечетность синуса, тангенса, котангенса. Напомним, что функция \(f(x)\) называется четной, если \(f(-x)=f(x)\) . Функция называется нечетной, если \(f(-x)=-f(x)\) . По окружности видно, что косинус угла \(\alpha\) равен косинусу угла \(-\alpha\) при любых значениях \(\alpha\) : Таким образом, косинус — четная функция, значит, верна формула \[<\Large<\cos(-x)=\cos x>>\] По окружности видно, что синус угла \(\alpha\) противоположен синусу угла \(-\alpha\) при любых значениях \(\alpha\) : Таким образом, синус — нечетная функция, значит, верна формула \[<\Large<\sin(-x)=-\sin x>>\] Как показывает практика, один из сложнейших разделов математики, который встречается школьникам в ЕГЭ, — тригонометрия. С наукой о соотношениях сторон в треугольниках начинают знакомиться в 8 классе. Уравнения данного типа содержат переменную под знаком тригонометрических функций. Несмотря на то, что простейшие из них: \(sin x = a\) , \(cos x = a\) , \(tg x = a\) , \(ctg x = a\) — знакомы практически каждому школьнику, их выполнение зачастую вызывает сложности. В ЕГЭ по математике профильного уровня правильно решенное задание по тригонометрии оценивается очень высоко. Школьник может получить до 4 первичных баллов за верно выполненную задачу из данного раздела. Для этого искать к ЕГЭ шпаргалки по тригонометрии практически бессмысленно. Наиболее разумное решение — хорошо подготовиться к экзамену. Как это сделать?Для того чтобы тригонометрия в ЕГЭ по математике вас не пугала, воспользуйтесь при подготовке нашим порталом. Это удобно, просто и эффективно. В данном разделе нашего образовательного портала, открытом для учащихся как Москвы, так и других городов, представлены доступно изложенный теоретический материал и формулы по тригонометрии для ЕГЭ. Также ко всем математическим определениям мы подобрали примеры с подробным описанием хода их решения. Что нужно знать?Прежде всего необходимо выучить значения \(sin\) , \(cos\) , \(tg\) , \(ctg\) острых углов от \(0°\) до \(90°\) . Также при подготовке к ЕГЭ в Москве стоит запомнить основные методы решения заданий по тригонометрии. Следует учесть, что, выполняя задачи, вы должны привести уравнение к простейшему виду. Сделать это можно следующим образом:
При этом чаще всего учащемуся приходится в ходе решения использовать несколько из перечисленных методов. Читайте также:
| ||