Логическая операция с использованием связки если то называется
ФИО________________________________________________________________________________Контрольная работа_Логика_№1
Определите какой логической операции соответствует таблица истинности:
Запиши высказывания в виде логической формулы:
Если в кинотеатре идет неинтересный фильм или у меня нет денег, то я останусь дома.
Пришла весна, и растаял снег.
a ___________________________ b _________________________
Укажите порядок вычисления значения логического выражения: (К Ā) А → К
Сколько строк в таблице истинности для выражения: (К Ā) А → К
Сколько столбцов в таблице истинности для выражения: (К Ā) А → К
Постройте таблицу истинности выражения (К Ā) → К
ФИО________________________________________________________________________________
Контрольная работа_Логика_№1
Определите какой логической операции соответствует таблица истинности:
Запиши высказывание в виде логической формулы:
Мы сегодня пойдем с друзьями в кино или я завтра пойду в театр.
Если не купили вам пирожное и в кино не взяли вечером, то нужно на родителей обидеться.
a ___________________________ b _________________________
Укажите порядок вычисления значения логического выражения: ( Ā С) ↔ А С
Сколько строк в таблице истинности для выражения: ( Ā С) ↔ А С
Сколько столбцов в таблице истинности для выражения: ( Ā С) ↔ А С
Постройте таблицу истинности выражения: Ā (С →А)
ФИО________________________________________________________________________________
Контрольная работа_Логика_№1
Определите какой логической операции соответствует таблица истинности:
Запиши высказывание в виде логической формулы:
Обычно вечером я иду на тренировку или гуляю с собакой.
Если в расписании на завтра нет первого уроа, то я высплюсь.
a ___________________________ b _________________________
Укажите порядок вычисления значения логического выражения: ( К А) Ā → К
Сколько строк в таблице истинности для выражения: ( К А) Ā → К
Сколько столбцов в таблице истинности для выражения: ( К А) Ā → К
Постройте таблицу истинности выражения: ( К Ā) → К
ФИО________________________________________________________________________________Контрольная работа_Логика_№1
Определите какой логической операции соответствует таблица истинности:
Запиши высказывание в виде логической формулы:
Если за мной зайдут друзья, и мы пойдем гулять, тоя весело проведу время.
Если с другом вышел в путь, то веселей дорога.
a ___________________________ b _________________________
Укажите порядок вычисления значения логического выражения: (А С) ↔ Ā С
Сколько строк в таблице истинности для выражения: (А С) ↔ Ā С
Сколько столбцов в таблице истинности для выражения: (А С) ↔ Ā С
Постройте таблицу истинности выражения: С ↔ Ā С
ФИО________________________________________________________________________________Контрольная работа_Логика_№1
Определите какой логической операции соответствует таблица истинности:
Запиши высказывание в виде логической формулы:
Сегодня я буду участвовать в кроссе и если пробегу дистанциюбыстрее всех, то получу медаль.
Прозвенел звонок, и все побежали на перемену.
a ___________________________ b _________________________
Выберите книгу со скидкой:

Математика. Новый полный справочник школьника для подготовки к ЕГЭ
350 руб. 222.00 руб.

Дошкольная педагогика с основами методик воспитания и обучения. Учебник для вузов. Стандарт третьего поколения. 2-е изд.
350 руб. 963.00 руб.

Считаю и решаю: для детей 5-6 лет. Ч. 1, 2-е изд., испр. и перераб.
350 руб. 169.00 руб.

Начинаю считать: для детей 4-5 лет. Ч. 1, 2-е изд., испр. и перераб.
350 руб. 169.00 руб.

Считаю и решаю: для детей 5-6 лет. Ч. 2, 2-е изд., испр. и перераб.
350 руб. 169.00 руб.

Пишу буквы: для детей 5-6 лет. Ч. 2. 2-е изд, испр. и перераб.
350 руб. 169.00 руб.

Русско-английский словарик в картинках для начальной школы
350 руб. 163.00 руб.

ОГЭ. Литература. Новый полный справочник для подготовки к ОГЭ
350 руб. 205.00 руб.

ЕГЭ. Английский язык. Новый полный справочник для подготовки к ЕГЭ
350 руб. 171.00 руб.

Рисуем по клеточкам и точкам
350 руб. 248.00 руб.

ЕГЭ. Информатика. Новый полный справочник для подготовки к ЕГЭ
350 руб. 163.00 руб.

350 руб. 114.00 руб.
БОЛЕЕ 58 000 КНИГ И ШИРОКИЙ ВЫБОР КАНЦТОВАРОВ! ИНФОЛАВКА



- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы
- Стародубова Оксана ВладимировнаНаписать 4223 26.11.2015
Номер материала: ДВ-198231
- Информатика
- 9 класс
- Конспекты
Добавляйте авторские материалы и получите призы от Инфоурок
Еженедельный призовой фонд 100 000 Р
-
26.11.2015 738
-
26.11.2015 446
-
26.11.2015 1152
-
26.11.2015 344
-
26.11.2015 1105
-
26.11.2015 1478
-
26.11.2015 1588
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Чтобы обращаться к логическим высказываниям, им назначают имена.
Пусть через А обозначено высказывание “Тимур поедет летом на море”, а через В – высказывание “Тимур летом отправиться в горы”. Тогда составное высказывание “Тимур летом побывает и на море, и в горах” можно кратко записать как А и В. Здесь “и” – логическая связка, А.В – логические переменные, которые могут принимать только два значения – “истина” или “ложь”.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение:
1. Логическое отрицание (инверсия)
Операция, выражаемая символом “не” называется отрицанием и обозначается чертой над высказыванием.
Логическое отрицание (инверсия) образуется из высказывания с помощью добавления частицы “не” к сказуемому или использования оборота речи “неверно, что”.
Обозначение: не А. (Более подробно об обозначениях логических операций смотрите в хранилище файлов)
Нас интересует истинность высказывания, имеющего форму не А. Определяется она по специальной таблице истинности.

Из таблицы истинности следует, что инверсия высказывания истинна, когда высказывание ложно, и ложна, когда высказывание истинно.
2. Логическое умножение (конъюнкция)
Операция, выражаемая связкой “и” называется конъюнкцией или логическим умножением.
Логическое умножение (конъюнкция) образуется соединением двух высказываний в одно с помощью союза “и”.
А = Закончились уроки.
В = Дети идут домой.
А * В = “Закончились уроки и дети идут домой”.
Обозначение конъюнкции: A и B, А*В.
Таблица истинности.

Из таблицы истинности следует, что конъюнкция двух высказываний истинна тогда и только тогда, когда оба высказывания истинны, и ложна, когда хотя бы одно высказывание ложно.
3. Логическое сложение (дизъюнкция)
Операция, выражаемая связкой “или” называется дизъюнкцией или логическим сложением.
Логическое сложение (дизъюнкция) образуется соединением двух высказываний в одно с помощью союза “или”.
Высказывание “10 не делится на 2 или 5 не больше 3” - ложно, а высказывания
“10 делится на 2 или 5 больше 3”,
“10 делится на 2 или 5 не больше 3”
“10 не делится на 2 или 5 больше 3” - истинны.
Обозначение операции: А или В, A+B.
Таблица истинности.

Из таблицы истинности следует, что дизъюнкция двух высказываний ложна тогда и только тогда, когда оба высказывания ложны, и истинна, когда хотя бы одно высказывание истинно.
4. Логическое следование (импликация)
Каким образом импликация связывает два элементарных высказывания?
Пусть даны два высказывания:
А = “данный четырехугольник квадрат”.
В = “около данного четырехугольника можно описать окружность”.
Рассмотрим составное высказывание, которое понимается как “если данный четырехугольник квадрат, то около него можно описать окружность”.
Есть три варианта, когда импликация истинна:
· А истинно и В истинно, то есть данный четырехугольник квадрат, и около него можно описать окружность;
· А ложно и В ложно, то есть данный четырехугольник не является квадратом, но около него можно описать окружность (разумеется, это справедливо не для всякого четырехугольника);
· А ложно и В ложно, то есть данный четырехугольник не является квадратом, и около него нельзя описать окружность.
Ложен только один вариант: А истинно и В ложно, то есть данный четырехугольник является квадратом, но около него нельзя описать окружность.
Таблица истинности:

Из таблицы истинности следует, что импликация высказываний ложна тогда и только тогда, когда из истинного высказывания следует ложное (когда истинная предпосылка ведет к ложному выводу).
5. Логическое равенство (эквивалентность)
Операция, выражаемая связками “тогда и только тогда”, “необходимо и достаточно”, “…равносильно…”, называется эквиваленцией или двойной импликацией и обозначается знаком "двухстороняя стрелка".
“24 делится на 6 тогда и только тогда, когда 24 делится на 3”,
“23 делится на 6 тогда и только тогда, когда 23 делится на 3”
истинны, а высказывания
“24 делится на 6 тогда и только тогда, когда 24 делится на 5”,
“21 делится на 6 тогда и только тогда, когда 21 делится на 3”
Высказывания А и В, образующие составное высказывание эквивалентность могут быть совершенно не связаны по содержанию, например: “три больше двух” (А), “пингвины живут в Антарктиде” (В). Отрицаниями этих высказываний являются высказывания “три не больше двух” (не А), “пингвины не живут в Антарктиде” (не В). Образованные из высказываний А, В составные высказывания А º В и не А º не В истинны, а высказывания А º не В и не А º В - ложны.
Таблица истинности:

Итак, нами рассмотрены пять логических операций:
Импликацию можно выразить через дизъюнкцию и отрицание:
если А то В = не А + В
Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию:
А равносильно В = (не А + В) * (не В + А)
Таким образом, операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания.
Еще возникает необходимость говорить о приоритете выполнения логических операций. Они выполняются в следующем порядке:
· отрицание
· конъюнкция
· дизъюнкция
· импликация
· эквиваленция.
Порядок выполнения логических операций можно изменить, применив круглые скобки.
Выполните задания:
1. Определите, какие из высказываний в следующих парах являются отрицаниями друг друга, а какие нет:
Наука, изучающая формы, методы и законы правильного мышления, называется логикой. Она интересуется не содержанием мышления, а его формой, поэтому ее часто называют еще формальной логикой.
Форма мышления — это способ выражения мыслей или форма, по которой они строятся.
Правила, которые должны соблюдаться, чтобы на основании истинных суждений получить истинные выводы, — это законы мышления. Логика изучает эти законы и способы получения новых утверждений на основании уже имеющихся.
Математическая логика использует для установления истинности или ложности высказываний математические методы. Она пользуется специальным символьным языком, подобным языку математики, поэтому ее часто называют символьной логикой.
Алгебра логики — раздел математической логики, в котором методы алгебры используются в логических преобразованиях. Она изучает логические высказывания и методы установления их истинности или ложности с помощью алгебраических методов.
Таким образом, отличительной особенностью логических высказываний является возможность принимать одно из двух значений — истина и ложь. Истинность или ложность высказывания определяется вне алгебры логики — с помощью наблюдений, научных исследований, практических опытов и т. п.
В алгебре логики различают простые высказывания и сложные (составные), составленные из нескольких простых. Если в высказывании нельзя выделить некую часть, которая не совпадает по смыслу с исходным высказыванием и сама является высказыванием, то оно называется простым высказыванием. Простые высказывания обычно обозначаются латинскими буквами A, B, C и т. д.
В алгебре логики логические связки рассматриваются как логические операции. Они имеют свои названия и обозначения. Результаты применения каждой операции к логическим высказываниям (истинным или ложным) можно представить в виде таблицы. В ней указывают все возможные сочетания значений исходных логических высказываний и истинность или ложность результата. Такие таблицы называют таблицами истинности операции. Обычно в них используют обозначения логических значений 0 и 1 или ложь и истина.
Основные логические операции — отрицание, конъюнкция, дизъюнкция, исключающая дизъюнкция, следование, эквивалентность.
Высказывание ¬А ложно, когда А истинно, и истинно, когда А ложно.
Таблица истинности операции отрицания

Отрицание является унарной операцией. Унарная (одноместная) операция — это операция, которая применяется к одному операнду.
Остальные логические операции являются двуместными (бинарными). Бинарная (двуместная) операция — это операция, которая выполняется над двумя операндами.
Высказывание А ∧ В истинно только тогда, когда оба высказывания А и В истинны. Высказывание А ∧ В ложно только тогда, когда ложно хотя бы одно из высказываний А или В.
Таблица истинности операции конъюнкции

Высказывание А v В истинно только тогда, когда хотя бы одно из высказываний А или В истинно. Высказывание А v В ложно только тогда, когда оба высказывания А и В ложны.
Таблица истинности операции дизъюнкции

Высказывание А ⊕ В истинно только тогда, когда высказывания А и В имеют различные значения.
Таблица истинности операции строгой дизъюнкции

Для операции импликации справедливо утверждение, что из лжи может следовать все что угодно, а из истины — только истина. Таким образом, импликация А → В ложна только тогда, когда А истинно, а В ложно (из истинного высказывания следует ложное). Во всех остальных случаях импликация истинна.
Таблица истинности операции импликации

Если оба высказывания имеют различные логические значения, результатом операции эквивалентности всегда будет ложь. Если же оба простые высказывания ложны или оба истинны, то составное логическое высказывание всегда будет истинно.
Таблица истинности операции эквивалентности

Таким образом, сводная таблица истинности для всех основных логических операций имеет вид:
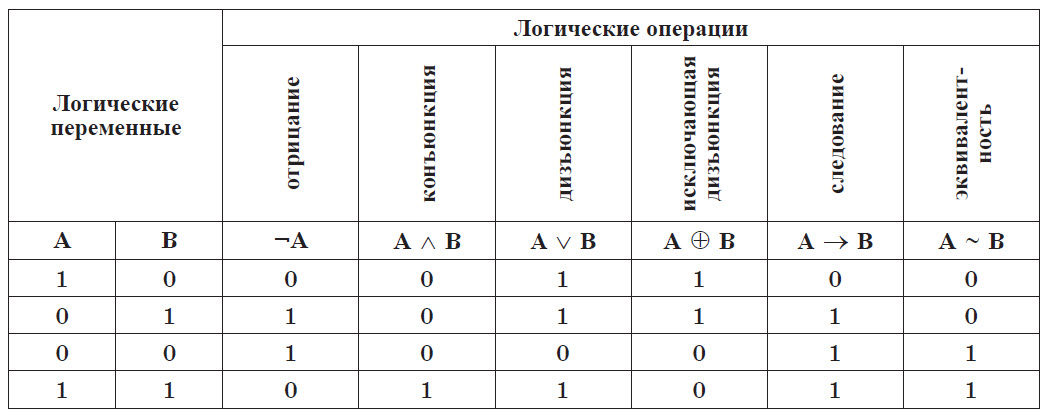
Логические высказывания могут быть записаны в виде формул (логических выражений). Логические выражения включают логические переменные, знаки логических операций, логические константы (истина и ложь) и скобки. Логические выражения принимают значения истина или ложь.
Правила построения логических выражений:
- любая логическая переменная или константа (истина и ложь) являются логическим выражением;
- если А — , то ¬А — тоже логическое выражение;
- если А и В — логические выражения, то А ∧ В; А v В ; А ⊕ В; А → В; А
В — тоже логические выражения.
Например, A ⊕ истина v В v ложь — логическое выражение; А v ⊕ В v ложь не является логическим выражением.
Логическое выражение, принимающее значение истина при любых значениях входящих в него переменных, называется тождественно–истинным выражением (тавтологией). Например, А v В v ¬А; (А ∧ ¬А) → В.
Логическое выражение, принимающее значение ложь при любых значениях входящих в него переменных, называется тождественно–ложным выражением (противоречием). Например, А ∧ ¬А; В
Логическое выражение, принимающее как значение ложь, так и значение истина при разных значениях входящих в него переменных, называется выполнимым выражением.
Для сложных логических выражений, содержащих несколько логических операций, определен порядок выполнения действий (приоритет): сначала операции отрицания, затем операции логического умножения, потом операции логического сложения и исключающего сложения, последними выполняются операции импликации и эквивалентности. Операции выполняются слева направо. Порядок выполнения может быть изменен с помощью скобок.
Приоритет выполнения логических операций в логических выражениях

Пример 1
Определить порядок выполнения логических операций в выражении.
Вычислить его значение, если А = 1, В = 0, С = 1.
¬А ∧ С v (A ⊕ В) ∧ В
Решение. Первыми вычисляются значения в скобках. Затем выполняются операции по приоритетам: самый высокий приоритет имеет операция отрицания, после нее, как в математике, следуют операции умножения, а затем сложения. Таким образом, порядок будет следующий: 
Тогда значение выражения ¬1 ∧ 1 v (1 ⊕ 0) ∧ 0 после вычисления отрицания и выражения в скобках: 0 ∧ 1 v 1 ∧ 0, после операций умножения: 0 v 0. Итог: 0.
Ответ: логическое выражение ложно.
Пример 2
Для каких из приведенных слов истинно следующее высказывание?
(Вторая буква гласная) ИЛИ (Первая буква гласная) И НЕ (Длина имени не больше 5 букв)
1) Олег 2) Марианна 3) Светлана 4) Ольга.
Ответ: 2) Марианна.
Связь между логическими операциями

Поэтому операции отрицания, логического сложения и логического умножения называют основными логическими операциями: их достаточно, чтобы построить любое логическое выражение.
Если логическое выражение содержит только операции отрицания, логического сложения и логического умножения, говорят, что выражение находится в нормальной форме.
Логические выражения, значения которых совпадают для всех наборов входящих в них переменных, называются равносильными, или эквивалентными.
Чтобы убедиться, что два выражения равносильны, можно построить для них таблицы истинности. Если в таблицах совпадут все значения, значит, выражения равносильны.
Пример 3
Проверить равносильность выражений А
E и (Ā ∧ Ē) v (A ∧ E).
Решение. Для проверки следует создать таблицу истинности, содержащую столько строк, сколько возможно наборов значений переменных, входящих в выражение. Для двух переменных (А и E) количество наборов равно четырем. К двум столбцам для значений переменных (А и E) нужно присовокупить количество столбцов, равное количеству операций в выражении. Таким образом, необходимо создать таблицу, содержащую 4 строки и 7 столбцов.
Заполним первые 2 столбца (А и E) всеми сочетаниями значений переменных. Запишем в качестве заголовков столбцов все операции выражения в порядке их выполнения (в соответствии с приоритетами и скобками). Рассчитаем значения этих операций: сначала выражения в скобках, затем результат их сложения.

Последний столбец содержит результирующее значение выражения. Он совпадает с таблицей истинности для операции эквивалентности. Следовательно, выражения равносильны.
Для сложных логических выражений с большим числом переменных определение их истинности путем построения таблиц истинности становится громоздким. В таких случаях применяют способы упрощения выражений. Под упрощением понимают равносильное преобразование выражения к его нормальной форме.
Нормальная форма выражения содержит только операции отрицания, конъюнкции и дизъюнкции и не содержит отрицания выражений и двойных отрицаний.
Для упрощения используют равносильные преобразования, которые иначе называют основными законами алгебры логики.
Тождественные преобразования логических выражений

Для всех тождественных преобразований выполняется закон двойственности: если в формуле преобразования заменить конъюнкцию на дизъюнкцию, дизъюнкцию — на конъюнкцию, значения 1 — на 0, 0 — на 1, то закон, сформулированный для конъюнкции, примет форму аналогичного закона для дизъюнкции, и наоборот.
Прежде всего при равносильных преобразованиях избавляются от отрицания выражений, потом — от логических операций исключающей дизъюнкции, следования и эквивалентности. Затем используют законы алгебры логики для уменьшения количества переменных в выражении.
Пример 4
Выбрать выражение, которое равносильно выражению (A ∧ B) v (Ā ∧ B).
1) A 2) A ∧ B 3) Ā ∧ B 4) B
Решение. В соответствии с законом склеивания (A ∧ B) v (Ā ∧ B) = B, следовательно, исходное выражение равносильно выражению В.
Ответ: 4) В.
Выражения, которые принимают логические значения (истина или ложь) в результате выполнения операций сравнения (больше >, меньше 3
1) 1 2) 2 3) 3 4) 4
Решение. В соответствии с приоритетами операций сначала следует выполнить операции сравнения, затем отрицания, а потом — конъюнкцию. Отрицанием высказывания М ≥ 10 является высказывание М 3. Для того чтобы это выражение (конъюнкция) было истинным, должны выполняться (т. е. быть истинными) оба неравенства. Следовательно, значение М должно быть больше 3, но меньше 10. Среди предложенных значений этому условию удовлетворяет только одно — число 4.
Ответ: 4) 4.
Задачи, подобные предыдущему примеру, можно решать и с помощью таблиц истинности.
Пример 6.
Для какого из приведенных ниже значений числа М истинно следующее выражение?
¬М ≥ 10 ∧ M > 3
1) 1 2) 2 3) 3 4) 4
Решение. Составим таблицу истинности: все операции выражения укажем в столбцах таблицы, все предложенные значения М укажем в ее строках. Рассчитаем значения таблицы:

Последний столбец содержит результат всего выражения. Истинным оно будет только для значения числа М, равного 4.
Ответ: 4) 4.
Пример 7.
В табличной форме представлены ежемесячные данные о продаже групп товаров за полгода. Сколько групп товаров демонстрировали рост продаж в весенние месяцы или вышли на уровень свыше 80 % в июне?

Решение. Переформулируем условие задачи: необходимо найти группы товаров, для которых (Март 80).
Введем обозначения:
А = (Март 80)
Тогда выражение можно записать как А ∧ В v С.
Логическое выражение состоит из одной конъюнкции и одной дизъюнкции. Значение выражения конъюнкции истинно только тогда, когда истинны оба составляющие его простых выражения ((Март
Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики).
Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).
Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно.
Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.
Примеры высказываний:
1. Москва – столица России.
2. Число 27 является простым.
3. Волга впадает в Каспийское море.
Высказывания 1 и 3 являются истинными. Высказывание 2 – ложным , потому что число 27 составное 27 = 3*3*3.
Следующие предложения высказываниями не являются:
- Давай пойдем гулять.
- 2*x > 8.
- a*x2 + b*x + c = 0.
- Который час?
Отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают.
С помощью высказываний устанавливаются свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно.
Примеры высказываний:
1. Сегодня светит солнце.
В математической логике не рассматривается конкретное содержание высказывания, важно только, истинно оно или ложно. Поэтому высказывание можно представить некоторой переменной величиной, значением которой может быть только 0 или 1. Если высказывание истинно, то его значение равно 1, если ложно - 0.
Простые высказывания назвали логическими переменными, а сложные - логическими функциями. Значения логической функции также только 0 или 1. Для простоты записи высказывания обозначаются латинскими буквами А, В, С.
В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные, большими буквами латинского алфавита.
Существуют разные варианты обозначения истинности и ложности логических переменных:
| Истина | И | True | T |
| Ложь | Л | False | F |
Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных логическими операциями.
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).
Логическое выражение - это символическая запись высказывания, состоящая из логических величин (констант или переменных), объединенных логическими операциями (связками).
Связки "НЕ", "И", "ИЛИ" заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции , при помощи которых можно записать любое логическое выражение.
Введем перечисленные логические операции.
Конъюнкция - логическое умножение (от латинского conjunctio - союз, связь):
В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
Если два высказывания соединены союзом "И", то полученное сложное высказывание истинно тогда и только тогда, когда истинны оба исходных высказывания.
Дизъюнкция - логическое сложение (от латинского disjunctio - разобщение, различие):
Дизъюнкция - это логическая операция, которая каждым двум простым (или исходным) высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.
В алгебре множеств дизъюнкции соответствует операция объединения множеств, т.е. множеству получившемуся в результате сложения множеств А и В соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.
Если два высказывания соединены союзом "ИЛИ", то полученное сложное высказывание истинно когда истинно хотя бы одно из составляющих высказываний.
Рассмотренные выше операции были двуместными (бинарными), т.е. выполнялись над двумя операндами (высказываниями). В алгебре логики определена и широко используется и одноместная (унарная) операция отрицание.
Инверсия - отрицание (от латинского disjunctio - разобщение, различие):
В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате отрицания множества А соответствует множество, дополняющее его до универсального множества.
Если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным.
Логическое следование (импликация):
| A | B | A=>B |
A => B
"Из А следует В"
Новое высказывание, полученное с помощью импликации, является ложным тогда и только тогда, когда условие (посылка А) - истинно, а следствие (заключение В) - ложно и истинно во всех остальных случаях.
| A | B | А В |
A B
"А равносильно В"
Новое высказывание, полученное с использованием эквивалентности, является истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
В алгебре логики логические связки и соответствующие им логические операции имеют специальные названия и обозначаются следующим образом:
Примеры записи сложных высказываний с помощью обозначения логических связок:
1. "Быть иль не быть - вот в чем вопрос." (В. Шекспир) А V A В
2. "Если хочешь быть красивым, поступи в гусары." (К. Прутков) А => В
Построение таблиц истинности и логических функций
Логическая функция - это функция, в которой переменные принимают только два значения: логическая единица или логический ноль. Истинность или ложность сложных суждений представляет собой функцию истинности или ложности простых. Эту функцию называют булевой функцией суждений f (a, b).
Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записывается набор аргументов, а в правой части - соответствующие значения логической функции. При построении таблицы истинности необходимо учитывать порядок выполнения логических операций.
Порядок выполнения логических операций в сложном логическом выражении:
Для изменения указанного порядка выполнения операций используются скобки.
Алгоритм построения таблиц истинности для сложных выражений:
1. Определить количество строк:
количество строк = 2 n + строка для заголовка,
n - количество простых высказываний.
2. Определить количество столбцов:
количество столбцов = количество переменных + количество логических операций;
- определить количество переменных (простых выражений);
- определить количество логических операций и последовательность их выполнения.
3. Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности с учетом таблиц истинности основных логических операций.
Пример: Составить таблицу истинности логического выражения:
D = А & (B Ú C).
1. Определить количество строк:
на входе три простых высказывания: А, В, С поэтому n = 3 и количество строк = 2 3 +1 = 9.
2. Определить количество столбцов:
- простые выражения (переменные): А, В, С;
- промежуточные результаты (логические операции):
А - инверсия (обозначим через E);
B Ú C - операция дизъюнкции (обозначим через F);
а также искомое окончательное значение арифметического выражения:
D = А & (B Ú C). т.е. D = E & F - это операция конъюнкции.
3. Заполнить столбцы с учетом таблиц истинности логических операций.
| A | B | C | E | F | E & F |
Построение логической функции по ее таблице истинности:
Попробуем решить обратную задачу. Пусть дана таблица истинности для некоторой логической функции:
| X | Y | Z |
Составить логическую функцию для заданной таблицы истинности.
Правила построения логической функции по ее таблице истинности:
1. Выделить в таблице истинности те строки, в которых значение функции равно 1.
2. Выписать искомую формулу в виде дизъюнкции нескольких логических элементов. Число этих элементов равно числу выделенных строк.
3. Каждый логический элемент в этой дизъюнкции записать в виде конъюнкции аргументов функции.
4. Если значение какого-либо аргумента функции в соответствующей строке таблице равно 0, то этот аргумент взять с отрицанием.
1. В первой и третьей строках таблицы истинности значение функции равно 1.
2. Так как строки две, получаем дизъюнкцию двух элементов: ( ) V ( ).
3. Каждый логический элемент в этой дизъюнкции запишим в виде конъюнкции аргументов функции X и Y: (X & Y) V (X & Y).
4. Берем аргумент с отрицанием если его значение в соответствующей строке таблицы равно 0 и получаем искомую функцию:
Z (X, Y) =( X & Y) V (X & Y).
Законы логики и правила преобразования логических выражений
1. Закон двойного отрицания (двойное отрицание исключает отрицание):
2. Переместительный (коммутативный) закон:
- для логического сложения: А Ú B = B Ú A;
- для логического умножения: A & B = B & A.
Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.
3. Сочетательный (ассоциативный) закон:
- для логического сложения: (А Ú B) Ú C = A Ú (B Ú C);
- для логического умножения: (A & B) & C = A & (B & C).
При одинаковых знаках скобки можно ставить произвольно или вообще опускать.
4. Распределительный (дистрибутивный) закон:
- для логического умножения: (A & B) Ú C = (A Ú C) & (B Ú C).
Закон определяет правило выноса общего высказывания за скобку.
6. Закон идемпотентности (от латинских слов idem — тот же самый и potens — сильный; дословно — равносильный):
- для логического сложения: А Ú A = A;
- для логического умножения: A & A = A .
Закон означает отсутствие показателей степени.
7. Законы исключения констант:
- для логического сложения: А Ú 1 = 1, А Ú 0 = A;
- для логического умножения: A & 1 = A, A & 0 = 0.
Невозможно, чтобы противоречащие высказывания были одновременно истинными.
Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.
10. Закон поглощения:
- для логического умножения: A & (A Ú B) = A.
Знание законов логики позволяет проверять правильность рассуждений и доказательств. Основываясь на законах, можно выполнять упрощение сложных логических выражений. Такой процесс замены сложной логической функции более простой, но равносильной ей, называется минимизацией функции.
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), другие - основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).
Нарушения законов логики приводят к логическим ошибкам и вытекающим из них противоречиям.
Упрощение формул.
Пример 1. Упростить формулу (А Ú В) & (А Ú С).
4. Аналогично предыдущему пункту вынесем за скобки высказывание А. A Ú B & A Ú B & C = A & (1 Ú B) Ú B & C = A Ú B & C.
Таким образом, мы доказали закон дистрибутивности.
Всякую формулу можно преобразовать так, что в ней не будет отрицаний сложных высказываний - все отрицания будут применяться только к простым высказываниям.
Пример 2. Упростить выражения 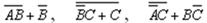
так, чтобы в полученных формулах не содержалось отрицания сложных высказываний.
Решение : 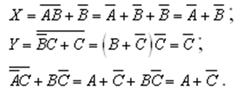
Читайте также:


