Математика шпор формула ?аза?ша
Шпаргалки по математике, алгебре и геометрии Шпаргалки по физике / Шпаргалки по химии
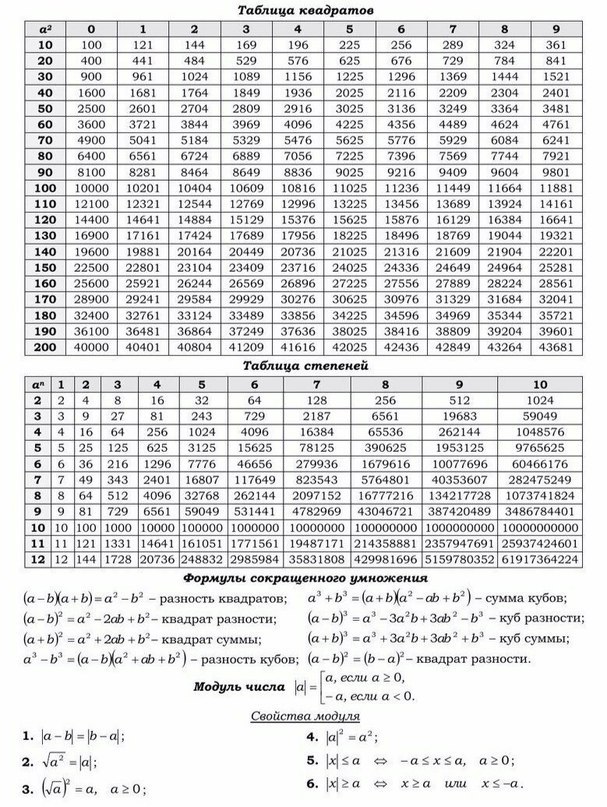
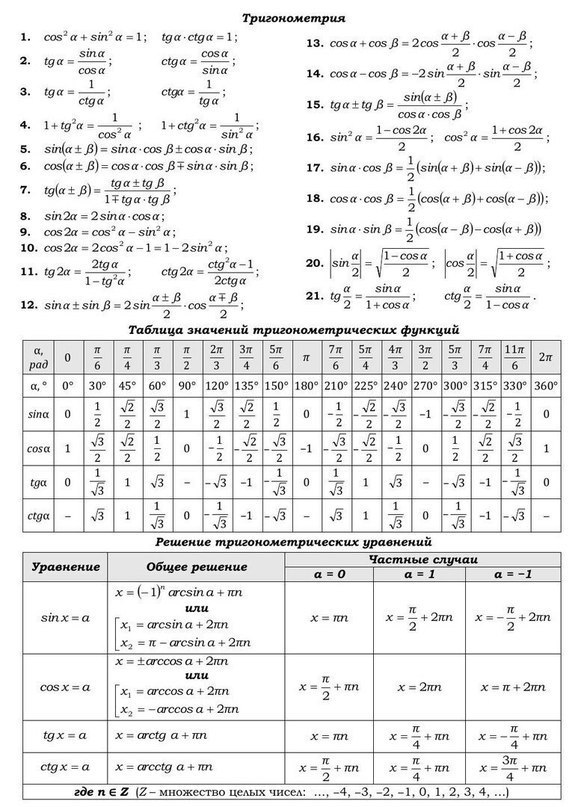
| Таблица квадратов. Таблица степеней. Формулы сокращенного умножения. Модуль числа. Свойства модуля: | Уравнения и неравенства с модулем. Последовательности и прогрессии. Метод кординат на плоскости. Скалярное произведение векторов. Расстояние между точками. | Тригонометрия - основные формулы. Таблица значений тригонометрических функций. Решение тригонометрических уравнений: | Четность и нечетность тригонометрических функций. Обратные тригонометрические функции. Формулы приведения. Знаки тригонометрических функций. Показательные уравнения и неравенства. |
 |  |  |  |
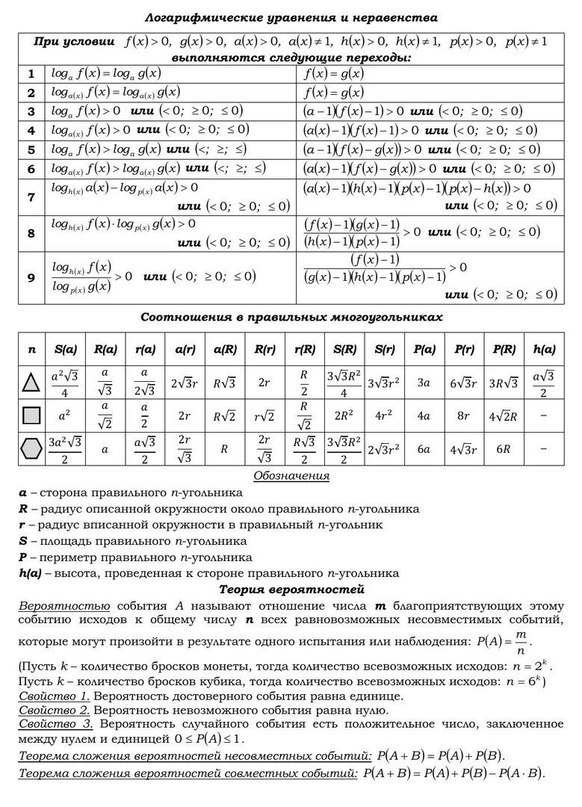
| Корень n-ой степени. Степени. Иррациональные уравнения и неравенства. Логарифм, свойства логарифмов | Логарифмические уравнения и неравенства. Соотношения в правильных многоугольниках. Теория вероятностей. Теоремы сложения вероятностей. | Логарифмические уравнения и неравенства. | Производная. Правила дифференцирования. Производная сложной функции. Уравнение касательной к графику функции в точке. |
 |  |  |  |
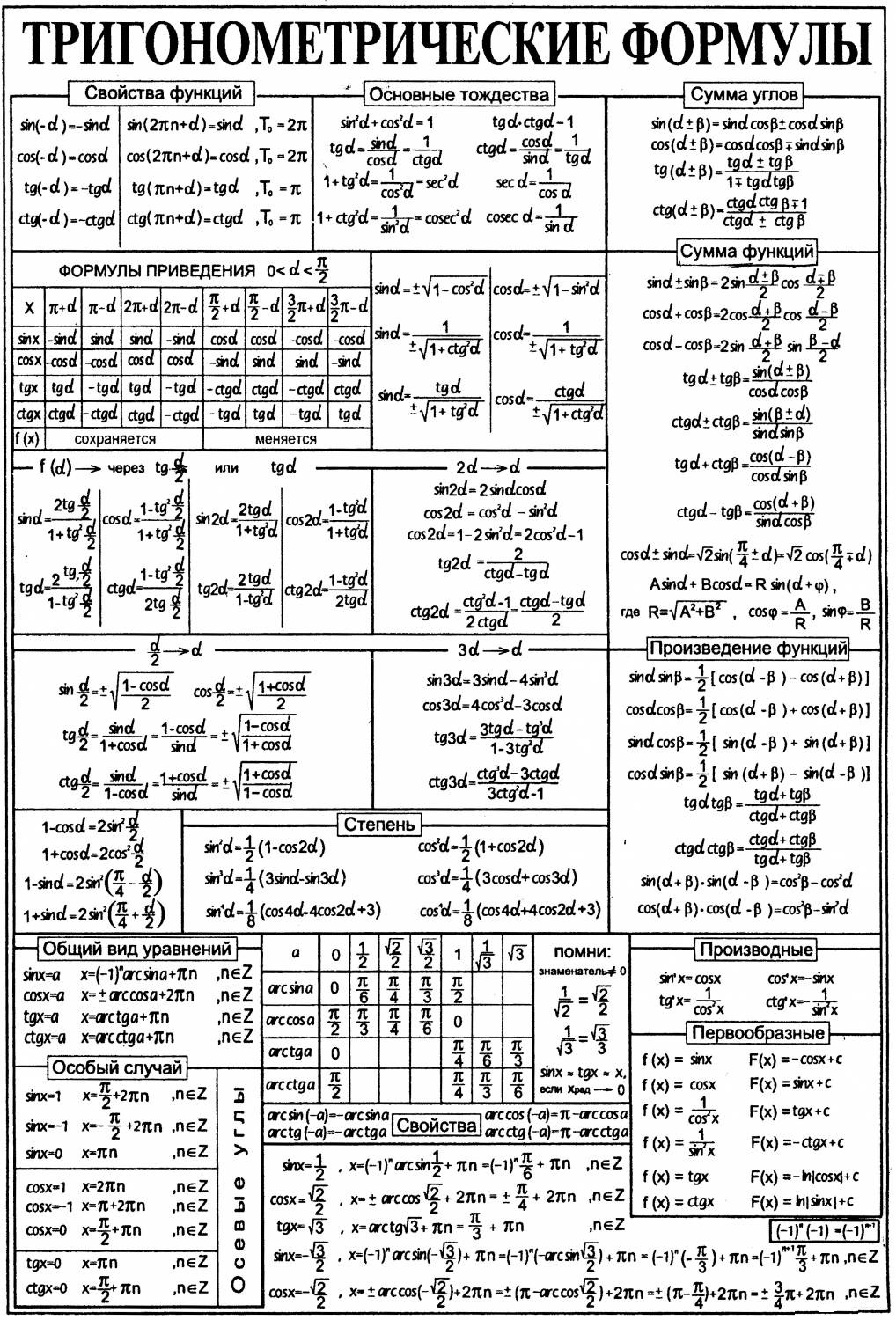
| Тригонометрические формулы. Свойства функций, основные тождества, сумма углов. Сумма функций, формулы приведения, особые случаи, степени, половинные, двойные и тройные углы. Обратные функции. | |||
 |
| Набор 2 - Алгебра. Линейная алгебра. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Свойства степеней. Формулы сокращенного умножения. Свойства арифметических корней. Модуль. Начала математического анализа: прогрессии арифметическая и геометрическая. Производная. Первообразная и интеграл. Среднее арифметическое и среднее геометрическое. | Тригонометрия. Основные формулы. Арксинус, арккосинус, арктангенс, арккотангенс. Четность функций. Значения тригонометрических функций некоторых углов. | Графики некоторых элементарных функций. Логарифмы. Решение квадратных, иррациональных, показательных, тригонометрических уравнений, уравнений с модулем | Квадратные неравенства. Неравенства с модулем. Логарифмические неравенства. Неравенства с модулем. Иррациональные неравенства. Показательные неравенства. Комбинаторика и бином Ньютона. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  |  |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
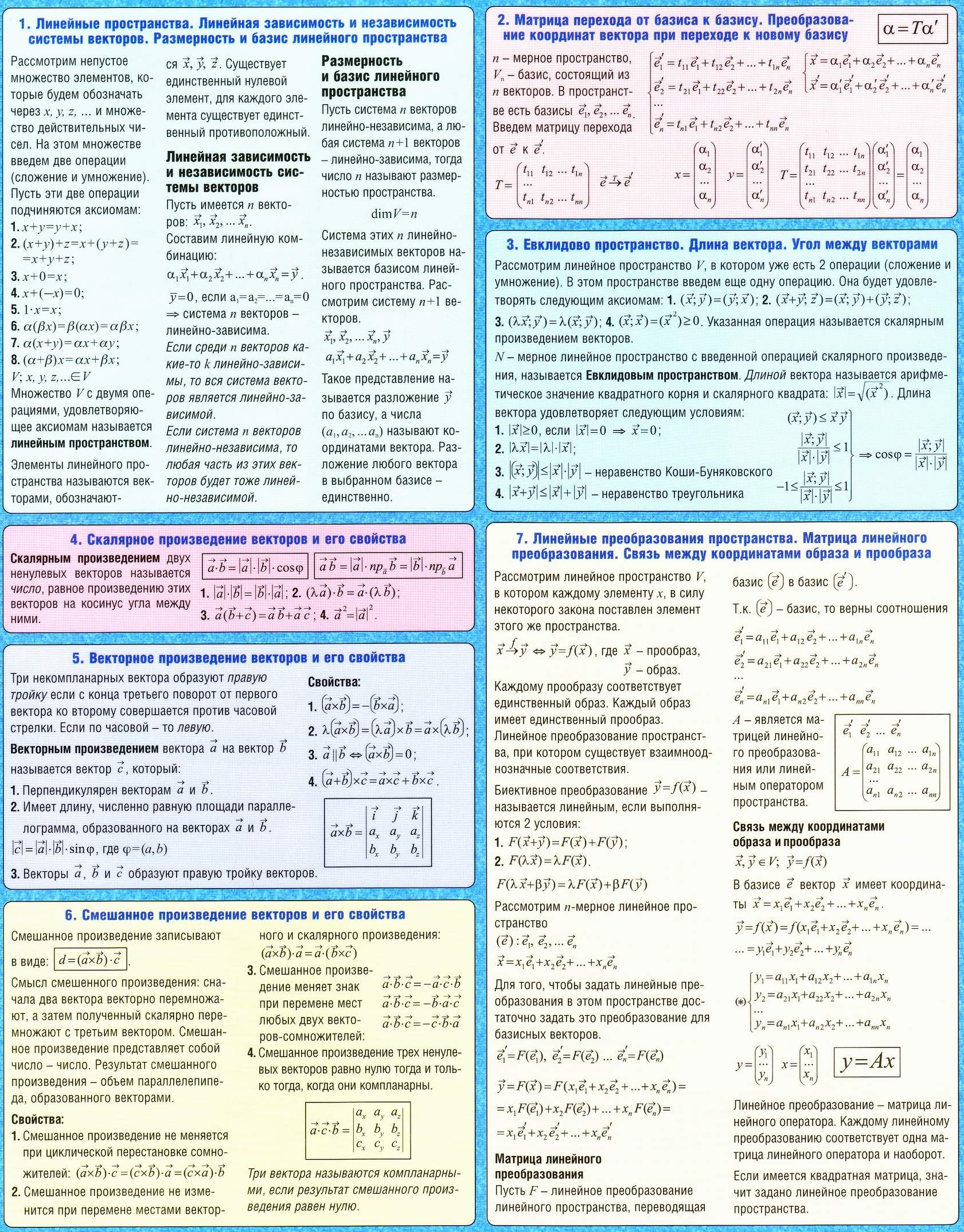
| Определение комплексного числа. Геометрическая интерпретация комплексного числа. Тригонометрическая форма комплексного числа. Показательная форма комплексного числа. Действия с комплексными числами. Последовательности, пределы последовательности. Теоремы о пределах числовых последовательностей. | Определение предела числовой функции. Односторонние пределы. Свойства пределов. Непрерывные функции и их свойства. Точки разрыва и их классификации. Замечательные пределы. Важные пределы. Теоремы о среднем. Правило Лопиталя. | Линейные пространства. Линейная зависимость и независимость системы векторов. Размерность и базис линейного пространства. Скалярное и векторное произведение векторов. Смешанное произведение векторов. Матрица перехода от базиса к базису. Преобразование координат вектора при переходе к новому базису. Евклидово пространство. Длина вектора. Угол между векторами. Линейные преобразования пространства. Матрица линейного преобразования. Связь между координатами образа и прообраза. | Связь между координатами одного и того же линейного оператора в разных базисах. Угол между прямой и плоскостью. Расстояние от точки до плоскости. Характеристические уравнения линейного оператора. Собственные векторы линейного оператора и их свтойства. Поверхности второго порядка. Плоскость в пространстве. Виды углов в пространстве. Уравнения плоскости. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  |  |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
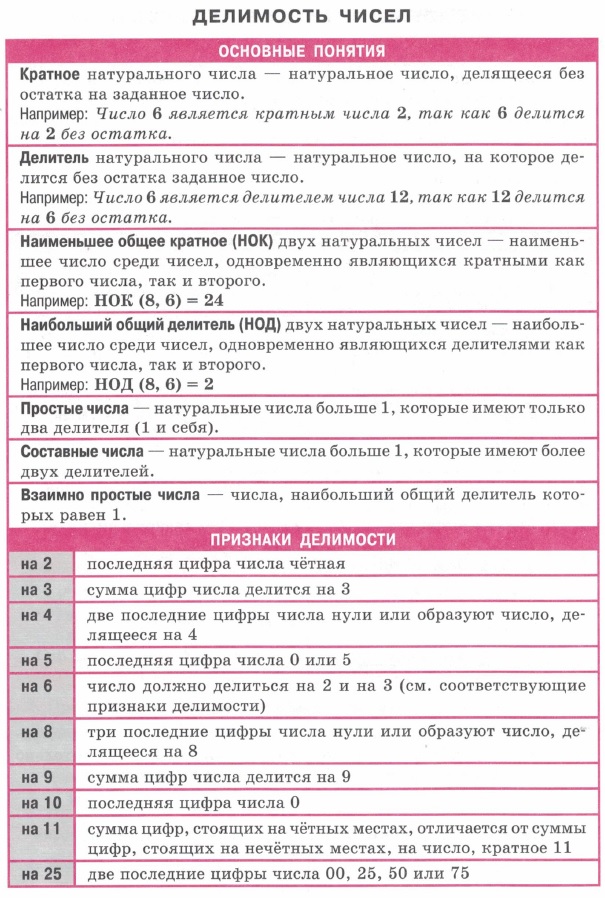
| Делимость чисел. Кратное. Делитель. НОК. НОД Простые и составные числа. Взаимно простые числа. | Числовые последовательности, члены, способы задания. Арифметическая и геометрическая прогрессии. Формулы. Характеристические свойства | Числа. Множества натуральных, целых, рациональных, действительных, иррациональных чисел. Арифметические действия с дробями. Модуль - свойства. | Решение квадратных уравнений. Формулы дискриминанта. Решение неполных квадратных уравнений. Теорема Виета. Алгоритм решения квадратного неравенства. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  |  |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Основные свойства функций. Понятие функции. Четность и нечетность. Периодичность. Нули функции. Промежутки знакопостоянства. Монотонность (возрастание, убывание). Асимптоты. Алгоритм описания фукнкции. |
Преобразование графиков функций у= f(x) в y=-f(x); y=f(-x); y=-f(-x); y=f(x-a); y=f(x)+b; y=f(ax); y=kf(x); y=|f(x)|; y=f(|x|). Построение графика обратной функции Степенные функции y=xn и y=x1/n, n∈Z. Свойства, графики. Квадратичная функция. Свойства степеней. Свойства арифметических корней. Формулы сокращенного умножения. Примеры значения степенных функций. Неравенства, понятия, строгие, нестрогие, решение. Свойства неравенств. Решение линейных неравенств. Решение квадратных неравенств. Метод интервалов при решении неравенств. Решение показательных неравенств. Решение логарифмическмх неравенств. Решение иррациональных неравенств. Решение неравенств с модулем. Часто применяемые неравенства Интегрирование функций. Понятие и основное свойство первообразной. Неопределенный интеграл. Правила интегрирования. Определенный интеграл. Формула Ньютона-Лейбница. Свойства и геометрический смысл определенного интеграла. Физический смысл определенного интеграла Уравнения прямой на плоскости. Общее уравнение прямой. Уравнение прямой "в отрезках". Уравнение прямой с угловым коэффициентом. Уравнение пучка прямых, проходящих через точку. Уравнение прямой, проходящей через 2 точки. Нормальное уранение прямой. Консультации и техническая Формулы, правила, свойства. Можно использовать для сдачи ЕГЭ и ОГЭ по математике. Для начала шпаргалка в компактном виде:
Формулы сокращенного умножения (а+b) 2 = a 2 + 2ab + b 2 (а-b) 2 = a 2 – 2ab + b 2 a 3 – b 3 = (a-b)( a 2 + ab + b 2 ) a 3 + b 3 = (a+b)( a 2 – ab + b 2 ) (a + b) 3 = a 3 + 3a 2 b+ 3ab 2 + b 3 (a – b) 3 = a 3 – 3a 2 b+ 3ab 2 - b 3 Свойства степеней a m/n = (a≥0, n ε N, m ε N) a - r = 1/ a r (a>0, r ε Q) a m · a n = a m + n a m : a n = a m – n (a≠0) Первообразная Если F’(x) = f(x), то F(x) – первообразная x n = x n +1 /n+1 + C a x = a x / ln a + C cos x = sin x + C 1/ sin 2 x = – ctg x + C 1/ cos 2 x = tg x + C sin x = – cos x + C Геометрическая прогрессия q – знаменатель прогрессии b n = b1 · q n – 1 – n-ый член прогрессии Модуль -a, если a Формулы cos и sin sin (x + π) = -sin x cos (x + π) = -cos x sin (x + 2πk) = sin x cos (x + 2πk) = cos x sin (x + π/2) = cos x Объемы и поверхности тел 1. Призма, прямая или наклонная, параллелепипед V = S·h 2. Прямая призма SБОК = p·h, p – периметр или длина окружности 3. Параллелепипед прямоугольный V = a·b·c; P = 2(a·b + b·c + c·a) P – полная поверхность 4. Куб: V = a 3 ; P = 6 a 2 S = 1/3 S·h; S – площадь основания 6. Пирамида правильная S =1/2 p·A A – апофема правильной пирамиды 7. Цилиндр круговой V = S·h = πr 2 h 8. Цилиндр круговой: SБОК = 2 πrh 9. Конус круговой: V=1/3 Sh = 1/3 πr 2 h 10. Конус круговой: SБОК = 1/2 pL= πrL Тригонометрические уравнения sin x = 1, x = π/2 + 2 πn sin x = -1, x = – π/2 + 2 πn cos x = 0, x = π/2 + 2 πn cos x = 1, x = 2πn cos x = -1, x = π + 2 πn Теоремы сложения cos (x +y) = cosx ·cosy – sinx ·siny cos (x -y) = cosx ·cosy + sinx ·siny sin (x +y) = sinx ·cosy + cosx ·siny sin (x -y) = sinx ·cosy – cosx ·siny tg (x ±y) = tg x ± tg y/ 1 - + tg x ·tg y ctg (x ±y) = tg x - + tg y/ 1± tg x ·tg y sin x ± sin y = 2 cos (x±y/2)· cos (x - +y/2) cos x ± cosy = -2 sin (x±y/2)· sin (x - +y/2) 1 + cos 2x = 2 cos 2 x; cos 2 x = 1+cos2x/2 1 – cos 2x = 2 sin 2 x; sin 2 x = 1- cos2x/2 a,b – основания; h – высота, c – средняя линия S = (a+b/2)·h = c·h а – сторона, d – диагональ S = a 2 = d 2 /2 a – сторона, d1, d2 – диагонали, α – угол между ними S = d1d2/2 = a 2 sinα 9. Правильный шестиугольник a – сторона S = (3√3/2)a 2 S = (L/2) r = πr 2 = πd 2 /4 Правила дифференцирования ( f (x) + g (x) )’ = f ’(x) + g’(x) (tg x)’ = 1/ cos 2 x (ctg x)’ = – 1/ sin 2 x (f (kx + m))’ = kf ’(kx + m) Уравнение касательной к графику функции Площадь S фигуры, ограниченной прямыми x = a , x = b Формула Ньютона-Лебница
sin x = b x = (-1) n arcsin b + πn cos x = b x = ± arcos b + 2 πn tg x = b x = arctg b + πn ctg x = b x = arcctg b + πn Теорема синусов : a/sin α = b/sin β = c/sin γ = 2R Теорема косинусов : с 2 =a 2 +b 2 -2ab cos y Неопределенные интегралы ∫ x n dx = (x n +1 /n+1) + C ∫ sin x dx = – cos x + C ∫ cos x dx = sin x + C ∫ dx/sin 2 x = -ctg + C ∫ dx/cos 2 x = tg + C ∫ x r dx = x r+1 /r+1 + C Логарифмы
Формулы двойного аргумента cos 2x = cos 2 x – sin 2 x = 2 cos 2 x -1 = 1 – 2 sin 2 x = 1 – tg 2 x/1 + tg 2 x sin 2x = 2 sin x · cos x = 2 tg x/ 1 + tg 2 x tg 2x = 2 tg x/ 1 – tg 2 x ctg 2x = ctg 2 x – 1/ 2 ctg x sin 3x = 3 sin x – 4 sin 3 x cos 3x = 4 cos 3 x – 3 cos x tg 3x = 3 tg x – tg 3 x / 1 – 3 tg 2 x sin s cos t = (sin (s+t) + sin (s+t))/2 sin s sin t = (cos (s-t) – cos (s+t))/2 cos s cos t = (cos (s+t) + cos (s-t))/2 Формулы дифференцирования x’ = 1 (sin x)’ = cos x (kx + m)’ = k (cos x)’ = – sin x (1/x)’ = – (1/x 2 ) ( ln x)’ = 1/x (e x )’ = e x ; (x n )’ = nx n-1 ;(log a x)’=1/x ln a Площади плоских фигур 1. Прямоугольный треугольник S = 1/2 a·b (a, b – катеты) 2. Равнобедренный треугольник S = (a/2)·√ b 2 – a 2 /4 3. Равносторонний треугольник S = (a 2 /4)·√3 (a – сторона) 4. Произвольный треугольник a,b,c – стороны, a – основание, h – высота, A,B,C – углы, лежащие против сторон; p = (a+b+c)/2 S = 1/2 a·h = 1/2 a 2 b sin C = a 2 sinB sinC/2 sin A= √p(p-a)(p-b)(p-c) a,b – стороны, α – один из углов; h – высота S = a·h = a·b·sin α cos (x + π/2) = -sin x Формулы tg и ctg tg x = sin x/ cos x; ctg x = cos x/sin x ctg (x + πk) = ctg x ctg (x ± π) = ± ctg x tg (x + π/2) = – ctg x ctg (x + π/2) = – tg x sin 2 x + cos 2 x =1 1 + tg 2 x = 1/ cos 2 x 1 + ctg 2 x = 1/ sin 2 x tg 2 (x/2) = 1 – cos x/ 1 + cos x cos 2 (x/2) = 1 + cos x/ 2 sin 2 (x/2) = 1 – cos x/ 2 P = 4 πR 2 = πD 2 V = πh 2 (R-1/3h) = πh/6(h 2 + 3r 2 ) SБОК = 2 πRh = π(r 2 + h 2 ); P= π(2r 2 + h 2 ) V = 1/6 πh 3 + 1/2 π(r 2 + h 2 )· h; 14. Шаровой сектор: V = 2/3 πR 2 h’ где h’ – высота сегмента, содержащего в секторе Формула корней квадратного уравнения ax 2 + bx + c = 0 (a≠0) Если D=0, то x = -b/2a (D = b 2 -4ac) Если D>0, то x1,2 = -b± /2a Арифметическая прогрессия a n+1 = a n + d, где n – натуральное число d – разность прогрессии; a n = a 1 + (n – 1)·d – формула n-го члена Радиус описанной окружности около многоугольника R = a/ 2 sin 180/n Радиус вписанной окружности L = 2 πR S = πR 2 Площадь конуса Тангенс угла - отношение противолежащего катета к прилещащему. Котангенс – наоборот. Скачать шпаргалки по математикеСкачать всё это в компактном виде: matematika-shpory.doc. Рекомендуем: Шпаргалка для сдачи экзамена по математическому анализу (матану, матаналу - кому как больше нравится^^). Уже оформленная (в формате doc) - Вам останется лишь распечатать, вырезать небольшие квадраты ножницами и пользоваться готовыми шпорами. Вот вопросы, которые есть в данной шпаргалке:
Пример ответа на вопрос (но без математических значков): Пусть задана кривая L и T-произвольное разбиение отрезка [a,b]. Обозначим M0, M1,…,Mn -соответcвующие точки кривой. Ломаную M0,…Mn назовем ломаной, вписанной в кривую L и отвечающую заданному разбиению T отрезка [a,b]. Обозначим li=Mi-1 Mi – длину звена ломаной. Общая длина будет определятся выражением . . Определение 2. Кривая L называется спрямляемой, если множество Определение 3. Длиной дуги l кривой L называется Sup Лемма 1. Пусть разбаению T отрезка [a,b] соответсвует длина длина l ломаной, вписанной в кривую L. Если разбиение T’ получено из разбиения T путем добавления новых точек, то l’ > l. Свойства спрямляемых кривых: 2. Если спрямляемая кривая L при помощи конечного числа точек Mi разбита на конечное число кривых Li, то каждая Li спрямляема и ещё кое-что (см. в оригинале). 3. Пусть L задана параметрическим уравнением. Обозначим через l(t) длину участка Lt, точки которого определяются всеми значениями параметра t. Тогда l(t) будет непрерывной и возрастающей функцией параметра t. Доказательство. Здесь идёт длинное доказательство с формулами. Потом даны ещё одна теорема и лемма. Информация о работеПоможем подготовить работу любой сложностиСкачать файл с работойПомогла работа? Поделись ссылкойФормулы сокращенного умножения и разложения на множители: + + =180 Стереометрия Читайте также:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||