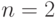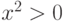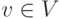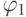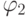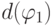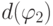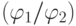Метод математической индукции шпора
Одним из самых важных методов математических доказательств по праву является метод математической индукции. Подавляющее большинство формул, относящихся ко всем натуральным числам n , могут быть доказаны методом математической индукции (к примеру, формула суммы n первых членов арифметической прогрессии 
, формула бинома Ньютона 
и т.п.).
В этой статье сначала остановимся на основных понятиях, далее рассмотрим сам метод математической индукции и разберем примеры его применения при доказательстве равенств и неравенств.
Навигация по странице.
- Индукция и дедукция.
- Метод математической индукции.
- Примеры доказательств уравнений и неравенств методом математической индукции.
Индукция и дедукция.
Индукцией называют переход от частных утверждений к общим. Напротив, переход от общих утверждений к частным называется дедукцией.
Пример частного утверждения: 254 делится на 2 без остатка.
Из этого частного утверждения можно сформулировать массу более общих утверждений, причем как истинных так и ложных. К примеру, более общее утверждение, что все целые числа, оканчивающиеся четверкой, делятся на 2 без остатка, является истинным, а утверждение, что все трехзначные числа делятся на 2 без остатка, является ложным.
Таким образом, индукция позволяет получить множество общих утверждений на основе известных или очевидных фактов. А метод математической индукции призван определить справедливость полученных утверждений.
В качестве примера, рассмотрим числовую последовательность: 
, n – произвольное натуральное число. Тогда последовательность сумм первых n элементов этой последовательности будет следующая

Исходя из этого факта, по индукции можно утверждать, что 
.
Доказательство этой формулы приведем чуть ниже.
Метод математической индукции.
В основе метода математической индукции лежит принцип математической индукции.
Он заключается в следующем: некоторое утверждение справедливо для всякого натурального n , если
- оно справедливо для n = 1 и
- из справедливости утверждения для какого-либо произвольного натурального n = k следует его справедливость для n = k+1 .
То есть, доказательство по методу математической индукции проводится в три этапа:
- во-первых, проверятся справедливость утверждения для любого натурального числа n (обычно проверку делают для n = 1 );
- во-вторых, предполагается справедливость утверждения при любом натуральном n=k ;
- в-третьих, доказывается справедливость утверждения для числа n=k+1 , отталкиваясь от предположения второго пункта.
Примеры доказательств уравнений и неравенств методом математической индукции.
Вернемся к предыдущему примеру и докажем формулу 
.
Доказательство.
Метод математической индукции предполагает доказательство в три пункта.
- Проверим равенство для n = 1 . Имеем
![]()
. Это равенство верное. - Предположим, что
![]()
есть справедливая формула.
Докажем, что 
отталкиваясь от справедливого равенства из второго пункта.
Сумма k+1 первых членов последовательности представляется как сумма первых k членов исходной числовой последовательности и k+1 ого члена:

Так как 
из второго пункта, то

Осталось привести дроби к общему знаменателю, привести подобные слагаемые, воспользоваться формулой сокращенного умножения квадрат суммы и произвести сокращение:

Следовательно, доказано равенство третьего пункта.
Таким образом, выполнены все три шага метода математической индукции и тем самым доказано наше предположение о формуле 
.
Давайте рассмотрим тригонометрическую задачу.
Докажите тождество 
.
Во-первых, проверяем справедливость равенства при n = 1 . Для этого нам понадобятся основные формулы тригонометрии.

То есть, равенство верно для n = 1 .
Во-вторых, предположим, что равенство верно для n = k , то есть справедливо тождество

В-третьих, переходим к доказательству равенства 
для n = k+1 , основываясь на втором пункте.

Так как по формуле из тригонометрии

то

Доказательство равенства из третьего пункта завершено, следовательно, исходное тождество доказано методом математической индукции.
Формула бинома Ньютона может быть доказана методом математической индукции.
Пример доказательства неравенства методом математической индукции можете посмотреть в разделе метод наименьших квадратов при выводе формул для нахождения коэффициентов аппроксимации.
Метод полного перебора конечного числа случаев, исчерпывающих все возможности, называется полной индукцией. Этот метод имеет крайне ограниченную область применения в математике, так как обычно математические утверждения касаются бесконечного множества объектов (например, натуральных чисел, простых чисел, квадратов и т.п.) и перебрать их невозможно.
Существует метод рассуждений, который позволяет заменить неосуществимый бесконечный перебор доказательством того, что если утверждение истинно в одном случае, то оно окажется истинным и в следущем за ним случае. Этот метод носит название математической индукции (или рассуждением от $n$ к $n+1$)
Основы метода математической индукции
В основе метода математической индукции (ММИ) лежит принцип математической индукции: утверждение $P(n)$ (где $n$ - натуральное число) справедливо при $\forall n \in N$, если:
- Утверждение $P(n)$ справедливо при $n=1$.
- Для $\forall k \in N$ из справедливости $P(k)$ следует справедливость $P(k+1)$.
Доказательство с помощью метода математической индукции проводится в два этапа:
- База индукции (базис индукции). Проверяется истинность утверждения при $n=1$ (или любом другом подходящем значении $n$)
- Индуктивный переход (шаг индукции). Считая, что справедливо утверждение $P(k)$ при $n=k$, проверяется истинность утверждения $P(k+1)$ при $n=k+1$.
Метод математической индукции применяется в разных типах задач:
- Доказательство делимости и кратности
- Доказательство равенств и тождеств
- Задачи с последовательностями
- Доказательство неравенств
- Нахождение суммы и произведения
Ниже вы найдете примеры решения задач, иллюстрирующие применение метода математической индукции, а также ссылки на полезные сайты и учебник и небольшой видеоурок по ММИ.
Математическая индукция: задачи и решения
Задача 1. Докажите, что $5^n-4n+15$ делится на 16 при всех $n \in N_0$.
Задача 2. Доказать, что при любом натуральном $n$ число $a_n$ делится на $b$.
$$a_n = 2n^3+3n^2+7n, \quad b=6.$$
Задача 3. Докажите методом математической индукции: $4^ <2n-1>+ 1$ кратно 5 для всех $n \ge 1$.
Задача 4. Используя метод математической индукции, докажите, что для любого натурального числа истинно следующее утверждение: $6^<2n-2>+3^
Задача 5. Доказать равенство
Задача 6. Доказать методом математической индукции:
Задача 7. Доказать неравенство:
Задача 8. Доказать утверждение методом математической индукции:
$$ \left(1-\frac<1><4>\right)\left(1-\frac<1><9>\right)\left(1-\frac<1><16>\right)\cdot . \cdot\left(1-\frac<1>
Задача 9. Доказать неравенство:
$$ 2!\cdot 4! \cdot . \cdot (2n)! \gt [(n+1)!]^n \quad (n \gt 2).$$
Задача 10. Докажите методом математической индукции неравенство Бернулли: $(1+a)^n \gt 1 + a\cdot n$ для всех $n\in N$ и $a \gt -1$, $a \in R$.
Задача 11. Доказать методом математической индукции:
Задача 12. Найдите сумму
$$1 \cdot 1! + 2 \cdot 2! + . . . + 2012 \cdot 2012! + 2013 \cdot 2013!$$
Заказать решение
Если вам нужна помощь с решением задач по любым разделам математики, обращайтесь в МатБюро. Выполняем контрольные и практические работы, ИДЗ и типовые расчеты на заказ. Стоимость задания от 60 рублей , оформление производится в Word, срок от 2 дней.
Полезные ссылки о ММИ
- ММИ: краткая теория и примеры решений Страничка виртуальной школы юного математика. Разобраны примеры (в том числе для геометрии) и даны задачи для самостоятельной работы.
- Виленкин Н.Я. Индукция. Комбинаторика Классическое пособие по методу математической индукции и комбинаторике (базовые понятия и примеры задач).
- Математическая индукция. Основные определения и 10 разобранных решений.
- Николаева С.А. Метод математической индукции: методическое пособие для учителей и учащихся.
- А. Шень Математическая индукция. Пособие для школьников, разобраны 29 задач, из них 19 с полным решением.
Кратенький видеоурок о ММИ
Математическая индукция - это весьма общий метод, который позволяет доказывать утверждения, зависящие от целочисленных параметров. Его можно сформулировать следующим образом.
Пусть P(n) - это некоторое утверждение, зависящее от целочисленного параметра n . Пусть, во-первых, утверждение P(n0) справедливо и пусть, во-вторых, для любого k >= n0 из справедливости P(k) следует справедливость P(k+1) . Тогда утверждение P(n) справедливо для всех n >= n0 .
Таким образом доказательство "по индукции" состоит из двух этапов.
- Базис (или основание) индукции состоит в доказательстве утверждения P(n0) для некоторого начального значения n0 ( обычно n0=1 , но это не обязательно).
- Шаг индукции состоит в предположении справедливости P(n) при n=k >= n0 и доказательстве из этого предположения справедливости утверждения P(k+1) .
Рассмотрим несколько примеров применения метода математической индукции .
Пример 1. Доказать, что при n>= 1
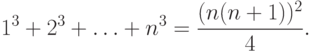
Базис индукции . При n=1 имеем
Шаг индукции . Допустим, что при n=k
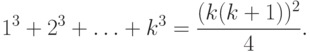
Докажем тогда, что при n=k+1
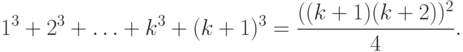

Таким образом, наше утверждение выполненопри всех n>= 1 .
Пример 2. Доказать, что для любого 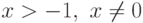
-1,\ x \ne 0" style="display: inline; ">, и натурального n>= 2 выполнено неравенство (1+x) n > 1 +nx (это неравенство называют неравенством Бернулли).
- Базис индукции . При
![]()
, учитывая, что![]()
0" style="display: inline; ">, имеем (1+x) 2 =1 +2x +x 2 > 1+2x . - Шаг индукции . Допустим, что при n=k неравенство справедливо, т.е. (1+x) k > 1 +kx . Покажем, что тогда оно выполнено и при n=k+1 . Действительно, так как 1+x > 0 , то умножив обе части на 1+x > 0 , получим (1+x) k (1+x)=(1+x) k+1 > (1+kx)(1+x)=1+ (k+1)x +kx 2 > 1+(k+1)x , что и требовалось.
В обычном понимании слово " индукция " означает переход от частных случаев к некоторому общему утверждению, а " дедукция " - получение результатов для частных случаев из некоторых общих утверждений, законов. В этом смысле метод математической индукции является дедуктивным, с его помощью доказываются общие утверждения (равенства, неравенства и т.п.). Он не дает способа для выдвижения общей гипотезы или угадывания общего правила или формулы по наблюдениям за отдельными частными случаями. Но этот метод позволяет проверять выдвинутые гипотезы. Для неверной гипотезы проверка провалится на шаге индукции.
Отметим также, что приведенная формулировка принципа математической индукции допускает разные эквивалентные варианты. В ряде случаев мы будем использовать вариант, в котором шаг индукции состоит в предположении справедливости P(n) при всех n и доказательстве из этого предположения справедливости утверждения P(k+1) .
Такая формулировка будет использоваться, в частности, при доказательствах индукцией по построению объекта.
В дискретной математике и в информатике многие классы объектов определяются индуктивно. В таких определениях явно или неявно участвует некоторая функция , задающая "сложность" объекта, и индукция идет по значениям этой функции. На базисном шаге определяются объекты минимальной сложности (обычно они имеют сложность 0), а индукционный шаг определения заключается в том, что из объектов меньшей сложности с помощью некоторых операций (операторов, конструкций) строятся объекты большей сложности.
Для доказательства некоторого свойства объектов индуктивно определенного класса метод математической индукции применяется в следующем виде.
- Базис индукции состоит в проверке требуемого свойства у объектов минимальной сложности.
- Шаг индукции состоит в предположении справедливости доказываемого свойства
- у всех объектов класса, имеющих сложность , и проверке того, что все объекты большей сложности (обычно, сложности k+1 ), получаемые из них с помощью используемых при определении класса операций, также обладают требуемым свойством.
Рассмотрим эту схему на примере простых арифметических выражений.
Пример 2.1. Пусть V = 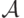
выражений ( слов) в объединенном алфавите 
, называемых арифметическими формулами. Одновременно будем определять меру сложности этих формул, назывемую их глубиной. Глубину формулы 
обозначим через 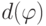
.
- Базис индукции . Каждая переменная
![]()
является арифметической формулой глубины 0, т.е.![]()
и d(v)=0 . - Шаг индукции . Пусть
![]()
и![]()
- арифметические формулы глубины![]()
и![]()
, соответственно. Тогда выражения- (а)
![]()
, - (б)
![]()
, - (в)
![]()
, - (г)
![]()
,
- (а)
также являются арифметическими формулами из 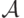
и каждая из этих формул имеет глубину 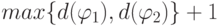
.
Пусть w=w1w2 . wn - произвольное слово в алфавите 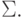
Скажем, что скобки в w расставлены правильно, если для каждого i число левых скобок в слове w (i) =w1w2 . wi не меньше числа правых скобок, а во всем слове w число левых скобок равно числу правых.
Докажем, что в каждой арифметической формуле из 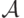
скобки расставлены правильно.

-
Главная
- Список секций
- Математика
- МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ



МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ

Введение
Данная тема является актуальной, так как каждый день люди решают различные задачи, в которых они применяют разные методы решения, но есть задания, в которых не обойтись без метода математической индукции, и в таких случаях будут очень полезны знания в данной области.
Я выбрал данную тему для исследования, потому что в школьной программе методу математической индукции уделяют мало времени, ученик узнает поверхностнуюинформацию, которая поможетему получить лишь общее представление о данном методе, но чтобы углубленно изучить эту теорию потребуется саморазвитие. Действительно будет полезно поподробнее узнать о данной теме, так как это расширяет кругозор человека и помогает в решении сложных задач.
Цель работы:
Познакомиться с методом математической индукции, систематизировать знания по данной теме и применить её при решении математических задач и доказательстве теорем, обосновать и наглядно показать практическое значение метода математической индукции как необходимого фактора для решения задач.
Задачи работы:
Проанализировать литературу и обобщить знания по данной теме.
Разобраться в принципе метода математической индукции.
Исследовать применение метода математической индукции к решению задач.
Сформулировать выводы и умозаключения по проделанной работе.
Основная часть исследования
История возникновения:
Только к концу XIX века сложился стандарт требований к логической строгости, остающейся и до настоящего времени господствующими в практической работе математиков над развитием отдельных математических теорий.
Индукция - познавательная процедура, посредством которой из сравнения наличных фактов выводится обобщающее их утверждение.
В математике роль индукции в значительной степени состоит в том, что она лежит в основе выбираемой аксиоматики. После того как длительная практика показала, что прямой путь всегда короче кривого или ломанного, естественно было сформулировать аксиому: для любых трех точек А, В и С выполняется неравенство .
Осознание метода математической индукции как отдельного важного метода восходит к Блезу Паскалю и Герсониду, хотя отдельные случаи применения встречаются ещё в античные времена у Прокла и Эвклида. Современное название метода было введено де Морганом в 1838 году.
Метод математической индукции можно сравнить с прогрессом: мы начинаем с низшего, в результате логического мышления приходим к высшему. Человек всегда стремился к прогрессу, к умению логически развивать свою мысль, а значит, сама природа предначертала ему размышлять индуктивно.
Индукция и дедукция
Известно, что существуют как частные, так и общие утверждения, и на переходе от одних к другим и основаны два данных термина.
Индукция (от лат. inductio – наведение) – это переход в процессе познания от частного знания к общему.Другими словами, – это метод исследования, познания, связанный с обобщением результатов наблюдений и экспериментов.Особенностью индукции является ее вероятностный характер, т.е. при истинности исходных посылок заключение индукции только вероятно истинно и в конечном результате может оказаться как истинным, так и ложным.
Полная и неполная индукция
Индуктивное умозаключение – такая форма абстрактного мышления, в которой мысль развивается от знания меньшей степени общности к знанию большей степени общности, а заключение, вытекающее из посылок, носит преимущественно вероятностный характер.
В ходе исследования я выяснил, что индукция делится на два вида: полная и неполная.
Полной индукцией называется умозаключение, в котором общий вывод о классе предметов делается на основании изучения всех предметов этого класса.
Например,пусть требуется установить, что каждое натуральное чётное число n в пределах 6≤ n≤ 18 представимо в виде суммы двух простых чисел. Для этого возьмём все такие числа и выпишем соответствующие разложения:
6=3+3; 8=5+3; 10=7+3; 12=7+5;14=7+7; 16=11+5; 18=13+5;
Данные равенства показывают, что каждое из интересующих нас чисел действительно представляется в виде суммы двух простых слагаемых.
Рассмотрим следующий пример: последовательность yn= n 2 +n+17; Выпишем первые четыре члена: у1=19; y2=23; y3=29; y4=37; Тогда мы можем предположить, что вся последовательность состоит из простых чисел. Но это не так, возьмем y16= 16 2 +16+17=16(16+1)+17=17*17. Это составное число, значит наше предположение неверно, таким образом, неполная индукция не приводит к вполне надежным выводам, но позволяет сформулировать гипотезу, которая в дальнейшем требует математического доказательства или опровержения.
Метод математической индукции
Полная индукция имеет в математике лишь ограниченное применение. Многие интересные математические утверждения охватывают бесконечное число частных случаев, а провести проверку для всех этих ситуаций мы не в состоянии.Но как осуществить проверку бесконечного числа случаев? Такой способ предложили Б.Паскаль и Я.Бернулли, это метод математической индукции, в основе которого лежит принцип математической индукции.
Если предложение А(n), зависящее от натурального числа n, истинно для n=1 и из того, что оно истинно для n=k (где k-любое натуральное число), следует, что оно истинно и для следующего числа n=k+1, то предположение А(n) истинно для любого натурального числа n.
В ряде случаев бывает нужно доказать справедливость некоторого утверждения не для всех натуральных чисел, а лишь для n>p, где p-фиксированное натуральное число. В этом случае принцип математической индукции формулируется следующим образом:
Если предложение А(n) истинно при n=p и если А(k) А(k+1) для любого k>p, то предложение А(n) истинно для любого n>p.
Алгоритм (он состоит из четырех этапов):
1.база ( показываем, что доказываемое утверждение верно для некоторых простейших частных случаев ( п= 1));
2.предположение (предполагаем, что утверждение доказано для первых к случаев); 3.шаг ( в этом предположении доказываем утверждение для случая п= к + 1); 4.вывод ( утверждение верно для всех случаев, то есть для всех п).
Заметим, что Методом математической индукции можно решать не все задачи, а только задачи, параметризованные некоторой переменной. Эта переменная называется переменной индукции.
Применение метода математической индукции
Применим всю данную теорию на практике и выясним, в каких задачах применяется данный метод.
Задачи на доказательство неравенств.
Пример 1.Доказать неравенство Бернулли(1+х)n≥1+n х, х>-1, n € N.
Докажем с помощью метода математической индукции.
1) При n=1 неравенство справедливо, так как 1+х≥1+х
2) Предположим, что неравенство верно для некоторого n=k, т.е.
Умножив обе части неравенства на положительное число 1+х, получим
(1+x) k+1 ≥(1+kx)(1+ x) =1+(k+1) x + kx 2
Учитывая, что kx 2 ≥0, приходим к неравенству
Таким образом, из допущения, что неравенство Бернулли верно для n=k, следует, что оно верно для n=k+1. На основании метода математической индукции можно утверждать, что неравенство Бернулли справедливо для любого n € N.
Пример 2. Доказать, что при любом натуральном n>1, .
Докажем с помощью метода математической индукции.
Обозначим левую часть неравенства через.
1), следовательно, при n=2 неравенство справедливо.
2)Пусть при некоторомk. Докажем, что тогда и . Имеем , .
Сравнивая и , имеем , т.е. .
При любом натуральном k правая часть последнего равенства положительна. Поэтому . Но , значит, и.Мы доказали справедливость неравенства при n=k+1, следовательно, в силу метода математической индукции, неравенство справедливо для любого натурального n>1.
Задачи на доказательство тождеств.
Пример 1. Доказать, что для любого натурального n справедливо равенство:
1 3 +2 3 +3 3 +…+n 3 =n 2 (n+1) 2 /4.
Пусть n=1, тогда Х1=1 3 =1 2 (1+1) 2 /4=1.
Мы видим, что при n=1 утверждение верно.
2) Предположим, что равенство верно при n=kXk=k 2 (k+1) 2 /4.
3) Докажем истинность этого утверждения для n=k+1, т.е.Xk+1=(k+1) 2 (k+2) 2 /4. Xk+1=1 3 +2 3 +…+k 3 +(k+1) 3 =k 2 (k+1) 2 /4+(k+1) 3 =(k 2 (k+1) 2 +4(k+1) 3 )/4=(k+1) 2 (k 2 +4k+4)/4=(k+1) 2 (k+2) 2 /4.
Из приведённого доказательства видно, что утверждение верно при n=k+1, следовательно, равенство верно при любом натуральном n.
Пример 2. Доказать, что при любом натуральном nсправедливо равенство
1) Проверим, что это тождество верно приn = 1.; - верно.
2) Пусть тождество верно и для n = k, т.е..
3)Докажем, что это тождество верно и для n = k + 1, т.е.;
Т.к. равенство верно при n=kи n=k+1, то оно справедливо при любом натуральном n.
Задачи на суммирование.
Пример 1.Доказать, что 1+3+5+…+(2n-1)=n 2 .
Решение: 1) Имеем n=1=1 2 . Следовательно, утверждение верно при n=1, т.е. А(1) истинно.
2) Докажем, что А(k) A(k+1).
Пусть k-любое натуральное число и пусть утверждение справедливо для n=k, т.е.1+3+5+…+(2k-1)=k 2 .
Докажем, что тогда утверждение справедливо и для следующего натурального числа n=k+1, т.е. что
В самом деле,1+3+5+…+(2k-1)+(2k+1)=k 2 +2k+1=(k+1) 2 .
Итак, А(k) А(k+1). На основании принципа математической индукции заключаем, что предположение А(n) истинно для любого n N.
Пример 2. Доказать формулу, n – натуральное число.
Решение: При n=1 обе части равенства обращаются в единицу и, следовательно, первое условие принципа математической индукции выполнено.
Предположим, что формула верна при n=k, т.е. .
Прибавим к обеим частям этого равенства и преобразуем правую часть. Тогда получим
Таким образом, из того, что формула верна при n=k, следует, что она верна и при n=k+1, то это утверждение справедливо при любом натуральном n.
Задачи на делимость.
Пример 1. Доказать, что (11 n+2 +12 2n+1 ) делится на 133 без остатка.
Решение: 1) Пусть n=1, тогда
11 3 +12 3 =(11+12)(11 2 -132+12 2 )=23× 133.
(23× 133) делится на 133 без остатка, значит при n=1 утверждение верно;
2) Предположим, что (11 k+2 +12 2k+1 ) делится на 133 без остатка.
3) Докажем, что в таком случае
(11 k+3 +12 2k+3 ) делится на 133 без остатка. Действительно, 11 k+3 +12 2л+3 =11×11 k+2 +
+12 2 ×12 2k+1 =11× 11 k+2 +(11+133)× 12 2k+1 =11(11 k+2 +12 2k+1 )+133× 12 2k+1 .
Полученная сумма делится на 133 без остатка, так как первое её слагаемое делится на 133 без остатка по предположению, а во втором одним из множителей является 133.
Итак, А(k)→ А(k+1), то опираясь на метод математической индукции, утверждение верно для любых натуральных n.
Пример 2. Доказать, что 3 3n-1 +2 4n-3 при произвольном натуральном n делится на 11.
Решение: 1) Пусть n=1, тогдаХ1=3 3-1 +2 4-3 =3 2 +2 1 =11 делится на 11 без остатка. Значит, при n=1 утверждение верно.
2) Предположим, что при n=k
Xk=3 3k-1 +2 4k-3 делится на 11 без остатка.
3) Докажем, что утверждение верно для n=k+1.
Xk+1=3 3(k+1)-1 +2 4(k+1)-3 =3 3k+2 +2 4k+1 =3 3 *3 3k-1 +2 4 *2 4k-3 =
=27 3 3k-1 +16* 2 4k-3 =(16+11)* 3 3k-1 +16* 2 4k-3 =16* 3 3k-1 +
+11* 3 3k-1 +16* 2 4k-3 =16(3 3k-1 +2 4k-3 )+11* 3 3k-1 .
Первое слагаемое делится на 11 без остатка, поскольку 3 3k-1 +2 4k-3 делится на 11 по предположению, второе делится на 11, потому что одним из его множителей есть число 11. Значит и сумма делится на 11 без остатка при любом натуральном n.
Задачи из реальной жизни.
Пример 1. Доказать, что сумма Sn внутренних углов любого выпуклого многоугольника равна (п- 2)π, где п — число сторон этого многоугольника:Sn = (п- 2)π (1).
Это утверждение имеет смысл не для всех натуральных п, а лишь для п > 3, так как минимальное число углов в треугольнике равно 3.
1) При п = 3 наше утверждение принимает вид: S3 = π. Но сумма внутренних углов любого треугольника действительно равна π. Поэтому при п = 3 формула (1) верна.
2) Пусть эта формула верна при n=k, то есть Sk = (k- 2)π, где k > 3. Докажем, что в таком случае имеет место и формула:Sk+1 = (k - 1)π.
Пусть A1A2 . AkAk+1—произвольный выпуклый (k + 1) -угольник (рис. 338).
Соединив точки A1 и Ak, мы получим выпуклый k-угольник A1A2 . Ak— 1Ak. Очевидно, что сумма углов (k + 1) -угольника A1A2 . AkAk+1 равна сумме углов k-угольника A1A2 . Ak плюс сумма углов треугольника A1AkAk+1. Но сумма углов k-угольника A1A2 . Ak по предположению равна (k - 2)π, а сумма углов треугольника A1AkAk+1 равна π. Поэтому
Итак, оба условия принципа математической индукции выполняются, и потому формула (1) верна при любом натуральном п > 3.
Приложение
Задачи с применением метода математической индукции при поступлении в ВУЗы.
Заметим, что при поступление в высшие учебные заведения также встречаются задачи, которые решаются данным методом. Рассмотрим их на конкретных примерах.
Пример 1.Доказать, что любом натуральном п справедливо равенство
1) При п=1 мы получаем верное равенство Sin.
2) Сделав предположение индукции, что при n=k равенство верно, рассмотрим сумму, стоящую в левой части равенства, при n=k+1;
3) Используя формулы приведения преобразуем выражение:
Тогда, в силу метода математической индукции равенство верно для любого натурального n.
Пример 2.Доказать, что для любого натурального n значение выражения 4n +15n-1 кратно 9.
1) При n=1 : 2 2 +15-1=18 - кратно 9 (т.к.18:9=2)
2) Пусть равенство выполняется для n=k: 4 k +15k-1 кратно 9.
3) Докажем, что равенство выполняется и для следующего числа n=k+1
4 k+1 +15(k+1)-1=4 k+1 +15k+15-1=4•4 k +60k-4-45k+18=4(4 k +15k-1)-9(5k-2)
4(4 k +15k-1) - кратно 9;
Следовательно и все выражение 4(4 k +15k-1)-9(5k-2) кратно 9, что и требовалось доказать.
Пример 3. Доказать, что при любом натуральном числе п выполняется условие : 1∙2∙3+2∙3∙4+…+ п(п+1)(п+2)=.
1) Проверим, что данная формула верна при п=1: Левая часть = 1∙2∙3=6.
Правая часть= . 6 = 6; верно при п=1.
2) Предположим, что данная формула верна при n=k:
3) Докажем, что данная формула верна при n=k+1:
Итак, данное условие верно в двух случаях и доказали, что верно при n=k+1, следовательно она верно при любом натуральном числе п.
Заключение
Подведем итоги, в процессе исследования я выяснил, в чем заключается индукция, которая бывает полной или неполной, познакомился с методом математической индукции, основанном на принципе математической индукции, рассмотрел множество задач с применением данного метода.
Также я узнал много новой информации, отличной от той, что включена в школьную программу.Изучая метод математической индукции я использовал различную литературу, ресурсы интернета, а также консультировался с педагогом.
Вывод: Обобщив и систематизировав знания по математической индукции, убедился в необходимости знаний по данной теме в реальной действительности. Положительным качеством метода математической индукции является его широкое применение в решении задач: в области алгебры, геометрии и реальной математики. Также эти знания повышают интерес к математике, как к науке.
Я уверен, что навыки, приобретенные в ходе работы, помогут мне в будущем.
Список литературы
Соминский И.С. Метод математической индукции. Популярные лекции по математике, выпуск 3-М.: Наука, 1974г.
Л. И. Головина, И. М. Яглом. Индукция в геометрии. — Физматгиз, 1961. — Т. 21. — 100 с. — (Популярные лекции по математике).
Дорофеев Г.В., Потапов М.К., Розов Н.Х. Пособие по математике для поступающих в вузы (Избранные вопросы элементарной математики) – Изд.5-е, перераб., 1976 – 638с.
А. Шень. Математическая индукция. — МЦНМО, 2004. — 36 с.
M.Л.Галицкий, А.М.Гольдман, Л.И.Звавич Сборник задач по алгебре: учеб.пособие для 8-9 кл. с углубл. изучением математики 7-е изд.— М.: Просвещение, 2001.—271 с
Макарычев Ю.Н., Миндюк Н.Г Дополнительные главы к школьному учебнику алгебры 9 класса. – М.: Просвещение, 2002.
Читайте также: