Уравнение кельвина для сферического мениска
Данное издание создано в помощь студентам вузов, которые хотят быстро подготовиться к экзаменам и сдать сессию без проблем. Пособие составлено с учетом Государственного образовательного стандарта.
- 1. Возникновение и основные этапы развития коллоидной химии. Предмет и объекты исследований коллоидной химии
- 2. Основные особенности дисперсных систем. Особенности ультрамикрогетерогенного состояния (наносостояния)
- 3. Различные типы классификации дисперсных систем. Лиофильные и лиофобные дисперсные системы
- 4. Дисперсность. Удельная поверхность дисперсных систем, методы ее измерения
- 5. Коллоиды. Примеры коллоидных систем, их распространенность в природе и значение для современной технологии
- 6. Оптические методы исследования дисперсных систем (нефелометрия, турбидиметрия)
- 7. Оптические свойства коллоидов. Статическое рассеяние света. Оптическая анизотропия
- 8. Поглощение света дисперсными системами, уравнение Бугера-Ламберта-Бера. Определение размеров коллоидных частиц
- 9. Поверхностные явления. Роль поверхностных явлений в процессах, протекающих в дисперсных системах
- 10. Поверхность раздела фаз. Свободная поверхностная энергия. Поверхностное натяжение. Адсорбция
- 11. Термодинамическое описание разделяющей поверхности
- 12. Адсорбция. Площадь, приходящаяся на одну молекулу в адсорбционном слое
- 13. Хроматографический адсорбционный анализ
- 14. Закономерности ионного обмена в коллоидных растворах. Ацидоиды. Роль pН в ионном обмене
- 15. Основные методы измерения поверхностного натяжения
- 16. Особенности ионного обмена в амфолитоидах, изоэлектрическое состояние амфолитоидов. Понятие об обменной емкости
- 17. Методы приготовления коллоидных растворов
- 18. Поверхность раздела между двумя конденсированными фазами. Правило Антонова. Межфазное натяжение
- 19. Капиллярное давление. Закон Лапласа
- 20. Закон Томсона. Капиллярная конденсация
- 21. Зависимость растворимости от кривизны поверхности дисперсных частиц (закон Гиббса-Оствальда-Фрейндлиха)
- 22. Смачивание. Закон Юнга (силовой и энергетический выводы)
- 23. Флотация
- 24. Определение краевого угла. Причины, затрудняющие это определение
- 25. Капиллярное поднятие жидкости, уравнение Жюрена
- 26. Поверхностные силы второго рода и расклинивающее давление. Линия трехфазного контакта (линия смачивания)
- 27. Использование ПАВ (вытеснение нефти, течение в невесомости и др.)
- 28. Разрушение и измельчение твердых тел как физико-химический процесс образования новой поверхности
- 29. Условие самопроизвольного распространения трещин. Влияние ПАВ на механические свойства твердых тел
- 30. Эффект Ребиндера. Основные особенности и формы проявления эффекта. Понижение прочности. Теория Гриффитса
- 31. Эффект Ребиндера: изменение прочности и пластичности как следствие снижения поверхностной энергии твердых тел
Приведённый ознакомительный фрагмент книги Коллоидная химия. Шпаргалка (С. В. Егоров, 2009) предоставлен нашим книжным партнёром — компанией ЛитРес.
20. Закон Томсона. Капиллярная конденсация
В пористых телах наряду с адсорбцией часто имеет место явление капиллярной конденсации. Под капиллярной конденсацией понимают конденсацию пара адсорбата при давлениях, которые меньше давления насыщенного пара. При адсорбции происходит образование тонкой пленки адсорбированного вещества на стенках пор, которые довольно хорошо смачиваются жидким сорбатом, в результате чего имеет место образование вогнутого мениска жидкости. Согласно закону Томсона давление пара, равновесное вогнутой поверхности, меньше упругости насыщенного пара. Следовательно, конденсация пара в порах над вогнутым мениском начинается при давлениях, которые меньше давления насыщенного пара. Изотерма адсорбции в случае капиллярной классификации принадлежит к одному из типов 2–5 по классификации Брунаура.
dW1 = [RT ln (p0 / p)] dm / M,
где М – молярная масса.
Однако при переносе данного количества вещества увеличивается радиус капли на величину dr и ее поверхность на величину ds, следовательно, происходит работа увеличения поверхности:
dW1 = [RT ln (p0 / p)] dm / M = —σds.
Преобразовав данное уравнение получим уравнение Томсона для выпуклой поверхности:
r = —2σ v / [RT ln p0 / p].
Уравнение Томсона для вогнутой поверхности имеет вид:
r = —2σv / [RT ln p / p0].
Уравнение Томсона находит широкое применение при исследовании пористой структуры сорбентов. Объем адсорбата, заполнившего пространство пор адсорбента при капиллярной конденсации при определенном давлении (при этом имеет место изотермический процесс) считается равным объему пор, имеющих определенный размер (радиус). Кривую распределения объемов пор по радиусам определяют по экспериментального построения десорбционной ветви изотермы адсорбции. Последняя имеет следующий вид:
а = f (p / ps), v = f(r), v = a / ρ, r = 2σ v / RT ln p / ps,
где p – давление пара над вогнутым мениском;
ps – давление насыщенного пара при данной температуре; r – плотность жидкости; a – величина адсорбции.
- 1. Возникновение и основные этапы развития коллоидной химии. Предмет и объекты исследований коллоидной химии
- 2. Основные особенности дисперсных систем. Особенности ультрамикрогетерогенного состояния (наносостояния)
- 3. Различные типы классификации дисперсных систем. Лиофильные и лиофобные дисперсные системы
- 4. Дисперсность. Удельная поверхность дисперсных систем, методы ее измерения
- 5. Коллоиды. Примеры коллоидных систем, их распространенность в природе и значение для современной технологии
- 6. Оптические методы исследования дисперсных систем (нефелометрия, турбидиметрия)
- 7. Оптические свойства коллоидов. Статическое рассеяние света. Оптическая анизотропия
- 8. Поглощение света дисперсными системами, уравнение Бугера-Ламберта-Бера. Определение размеров коллоидных частиц
- 9. Поверхностные явления. Роль поверхностных явлений в процессах, протекающих в дисперсных системах
- 10. Поверхность раздела фаз. Свободная поверхностная энергия. Поверхностное натяжение. Адсорбция
- 11. Термодинамическое описание разделяющей поверхности
- 12. Адсорбция. Площадь, приходящаяся на одну молекулу в адсорбционном слое
- 13. Хроматографический адсорбционный анализ
- 14. Закономерности ионного обмена в коллоидных растворах. Ацидоиды. Роль pН в ионном обмене
- 15. Основные методы измерения поверхностного натяжения
- 16. Особенности ионного обмена в амфолитоидах, изоэлектрическое состояние амфолитоидов. Понятие об обменной емкости
- 17. Методы приготовления коллоидных растворов
- 18. Поверхность раздела между двумя конденсированными фазами. Правило Антонова. Межфазное натяжение
- 19. Капиллярное давление. Закон Лапласа
- 20. Закон Томсона. Капиллярная конденсация
- 21. Зависимость растворимости от кривизны поверхности дисперсных частиц (закон Гиббса-Оствальда-Фрейндлиха)
- 22. Смачивание. Закон Юнга (силовой и энергетический выводы)
- 23. Флотация
- 24. Определение краевого угла. Причины, затрудняющие это определение
- 25. Капиллярное поднятие жидкости, уравнение Жюрена
- 26. Поверхностные силы второго рода и расклинивающее давление. Линия трехфазного контакта (линия смачивания)
- 27. Использование ПАВ (вытеснение нефти, течение в невесомости и др.)
- 28. Разрушение и измельчение твердых тел как физико-химический процесс образования новой поверхности
- 29. Условие самопроизвольного распространения трещин. Влияние ПАВ на механические свойства твердых тел
- 30. Эффект Ребиндера. Основные особенности и формы проявления эффекта. Понижение прочности. Теория Гриффитса
- 31. Эффект Ребиндера: изменение прочности и пластичности как следствие снижения поверхностной энергии твердых тел
Приведённый ознакомительный фрагмент книги Коллоидная химия. Шпаргалка (С. В. Егоров, 2009) предоставлен нашим книжным партнёром — компанией ЛитРес.
Давление насыщенного пара над искривленной поверхностью отличается от давления насыщенного пара над плоской поверхностью, что приводит к изменению химического потенциала над искривленной поверхностью и изменяет условия фазовых равновесий в дисперсных системах по сравнению с макрообъектами. Условием фазового равновесия является равенство химических потенциалов пара и жидкости:

где Р — давление насыщенного пара над искривленной поверхностью; Ps — давление насыщенного пара над плоской поверхностью. Приращение химического потенциала за счет лапласова давления при изменении кривизны поверхности для однокомпонентной системы в изотермических условиях соответствует работе расширения:

После подстановки Ар и необходимых преобразований получаем уравнение Томсона (Кельвина), связывающее давление Р, при котором пар будет насыщенным по отношению к искривленной поверхности, с радиусом кривизны г. 
_8 м при температуре 293 К. Равновесное давление СС14 при этой температуре составляет 13 000 Па, плотность СС14 — 1595 кг/м [1] , поверхностное натяжение — 25,68 • 10 _3 Дж/м 2 , М(СС14) = 154 • 10 [1] кг/моль. Имеем

2. Чем меньше размер капли, тем больше равновесное давление ее насыщенного пара, тем менее устойчиво ее состояние.
В полидисперсной системе с каплями различных размеров давление насыщенного пара над ними различно. Поэтому мелкие капли испаряются; испарившееся вещество может конденсироваться на поверхности более крупных частиц и на плоской поверхности (рис. 6.12). Такой процесс роста крупных частиц за счет исчезновения мелких называется изотермической перегонкой (переконденсацией). Таким образом, всякая полидисперсная система термодинамически неравновесна, а потому неустойчива.

Рис. 6.12. Изотермическая перегонка (переконденсация)
Вопросы практики
В атмосфере городского смога конденсация паров воды происходит на плоских гранях твердых частиц при относительной влажности около 100% (P/Ps
1), образующиеся плоские пленки воды способствуют конденсации и переконденсации мелких капель, поэтому количество осадков над городами в целом выше, чем в экологически чистых областях.

Вопросы практики
Повышенная растворимость высокодисперсных веществ применяется при производстве лекарственных препаратов коллоидного серебра и золота, обладающих бактерицидным действием.
Термодинамическая неравновеснос гь таких систем обусловливает перекристаллизацию вещества — рост крупных кристаллов в пересыщенном растворе за счет растворения мелких. Образование сталактитов и сталагмитов, рудных месторождений некоторых металлов (медь, цинк) связано с изотермической перегонкой в пересыщенных гидротермальных растворах сульфидов, оксидов или других соединений этих металлов.
Интерактивный компонент
Как можно определить удельную поверхностную энергию на границе «твердое тело — жидкость>>?
Произведение растворимости BaS04 при 20°С ПР = 1,1 • 10 10 , что соответствует растворимости сравнительно крупных кристаллов 1,049 • 10 5 моль/л. Растворимость высокодисперсных частиц радиусом 3 • 10 7 м равна 1,255 ? 10 5 моль/л. Плотность сульфата бария — 4500 кг/м 3 . При подстановке этих данных в уравнение Томсона
Капиллярные явления, поверхностные явления на границе жидкости с др. средой, связанные с искривлением ее поверхности. Искривление поверхности жидкости на границе с газовой фазой происходит в результате действия поверхностного натяжения жидкости, которое стремится сократить поверхность раздела и придать ограниченному объему жидкости форму шара. Поскольку шар обладает минимальной поверхностью при данном объеме, такая форма отвечает минимуму поверхностной энергии жидкости, т.е. ее устойчивому равновесному состоянию. В случае достаточно больших масс жидкости действие поверхностного натяжения компенсируется силой тяжести, поэтому маловязкая жидкость быстро принимает форму сосуда, в который она налита, а ее своб. поверхность представляется практически плоской.
В отсутствие силы тяжести или в случае очень малых масс жидкость всегда принимает сферическую форму (капля), кривизна поверхности которой определяет мн. свойства вещества. Поэтому капиллярные явления ярко выражены и играют существенную роль в условиях невесомости, при дроблении жидкости в газовой среде (или распылении газа в жидкости) и образовании систем, состоящих из многих капель или пузырьков (эмульсий, аэрозолей,пен), при зарождении новой фазы капель жидкости при конденсации паров. пузырьков пара при вскипании, зародышей кристаллизации. При контакте жидкости с конденсированными телами (другой жидкостью или твердым телом) искривление поверхности раздела происходит в результате действия межфазного натяжения.
В случае смачивания, например, при соприкосновении жидкости с твердой стенкой сосуда, силы притяжения, действующие между молекулами твердого тела и жидкости, заставляют ее подниматься по стенке сосуда, вследствие чего примыкающий к стенке участок поверхности жидкости принимает вогнутую форму. В узких каналах, например, цилиндрических капиллярах, образуется вогнутый мениск - полностью искривленная поверхность жидкости (рис. 1).

Рис. 1. Капиллярное поднятие на высоту h жидкости, смачивающей стенки капилляра радиуса r; q - краевой угол смачивания.
Капиллярное давление. Так как силы поверхностного (межфазного) натяжения направлены по касательной к поверхности жидкости, искривление последней ведет к появлению составляющей, направленной внутрь объема жидкости. В результате возникает капиллярное давление, величина которого Dp связана со средним радиусом кривизны поверхности r 0 уравнением Лапласа:
Dp = p 1 - p 2 = 2s 12 /r 0 , (1)
где p 1 и p 2 - давления в жидкости 1 и соседней фазе 2 (газе или жидкости), s 12 - поверхностное (межфазное) натяжение.
Если поверхность жидкости вогнута (r 0 1 2 и Dp 0 > 0) знак Dp изменяется на обратный. Отрицательное капиллярное давление, возникающее в случае смачивания жидкостью стенок капилляра, приводит к тому, что жидкость будет всасываться в капилляр до тех пор, пока вес столба жидкости высотой h не уравновесит перепад давления Dp. В состоянии равновесия высота капиллярного поднятия определяется формулой Жюрена:

где r 1 и r 2 - плотности жидкости 1 и среды 2, g - ускорение силы тяжести, r - радиус капилляра, q - краевой угол смачивания. Для несмачивающих стенки капилляра жидкостей cos q а = [2s 12 /(r 1 — r 2 )g] 1/2 . Она имеет размерность длины и характеризует линейный размер Z [ а, при котором становятся существенными капиллярные явления Так, для воды при 20 °С а = 0,38 см. При слабой гравитации (g : 0) значение а возрастает. На участке контакта частиц капиллярная конденсация приводит к стягиванию частиц под действием пониженного давления Dp р по сравнению с давлением насыщенного пара p s над плоской поверхностью при той же температуре Т. Эти изменения описываются уравнением Кельвина:

где 
- молярный объем жидкости, R - газовая постоянная. Понижение или повышение давления пара зависит от знака кривизны поверхности: над выпуклыми поверхностями (r 0 > 0) p > p s ; над вогнутыми (r 0 р s . . Так, над каплями давление пара повышено; в пузырьках, наоборот, понижено.
На основании уравнения Кельвина рассчитывают заполнение капилляров или пористых тел при капиллярной конденсации. Так как значения р различны для частиц разных размеров или для участков поверхности, имеющей впадины и выступы, уравнение (3) определяет и направление переноса вещества в процессе перехода системы к состоянию равновесия. Это приводит, в частности, к тому, что относительно крупные капли или частицы растут за счет испарения (растворения) более мелких, а неровности поверхности некристаллические тела сглаживаются за счет растворения выступов и залечивания впадин. Заметные различия давления пара и растворимости имеют место лишь при достаточно малых r 0 (для воды, например, при r 0 [ 0,1 мкм). Поэтому уравнение Кельвина часто используется для характеристики состояния коллоидных систем и пористых тел и процессов в них.
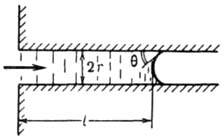
Рис. 2. Перемещение жидкости на длину l в капилляре радиуса r; q - краевой угол.
Капиллярная пропитка. Понижение давления под вогнутыми менисками - одна из причин капиллярного перемещения жидкости в сторону менисков с меньшим радиусом кривизны. Частным случаем этого является пропитка пористых тел - самопроизвольное всасывание жидкостей в лиофильные поры и капилляры (рис. 2). Скорость v перемещения мениска в горизонтально расположенном капилляре (или в очень тонком вертикальном капилляре, когда влияние силы тяжести мало) определяется ур-нием Пуазёйля:

где l - длина участка впитавшейся жидкости, h - ее вязкость, Dp - перепад давления на участке l , равный капиллярному давлению мениска: Dp = — 2s 12 cos q/r. Если краевой угол q не зависит от скорости v, можно рассчитать количество впитавшейся жидкости за время t из соотношения:
l ( t ) = (rts 12 cos q/2h) l/2 . (5)
Если q есть функция v , то l и v связаны более сложными зависимостями.
Уравнения (4) и (5) используют для расчетов скорости пропитки при обработке древесины антисептиками, крашении тканей, нанесении катализаторов на пористые носители, выщелачивании и диффузионном извлечении ценных компонентов горных пород и др. Для ускорения пропитки часто используют ПАВ, улучшающие смачивание за счет уменьшения краевого угла q. Один из вариантов капиллярной пропитки - вытеснение из пористой среды одной жидкости другой, не смешивающейся с первой и лучше смачивающей поверхность пор. На этом основаны, например, методы извлечения остаточной нефти из пластов водными растворами ПАВ, методы ртутной порометрии. Капиллярное впитывание в поры растворов и вытеснение из пор несмешивающихся жидкостей, сопровождающиеся адсорбцией и диффузией компонентов, рассматриваются физико-химической гидродинамикой.
Помимо описанных равновесных состояний жидкости и ее движения в порах и капиллярах, к капиллярные явления относят также равновесные состояния очень малых объемов жидкости, в частности тонких слоев и пленок. Эти капиллярные явления часто называют капиллярные явления II рода. Для них характерны, например, зависимость поверхностного натяжения жидкости от радиуса капель и линейное натяжение. Капиллярные явления впервые исследованы Леонардо да Винчи (1561), Б. Паскалем (17 в.) и Дж. Жюреном (18 в.) в опытах с капиллярными трубками. Теория капиллярных явлений развита в работах П. Лапласа (1806), Т. Юнга (1804), А. Ю. Давыдова (1851), Дж. У. Гиббса (1876), И. С. Громеки (1879, 1886). Начало развития теории капиллярных явлений II рода положено трудами Б. В. Дерягина и Л. М. Щербакова.
Лит.: Адамсон А., Физическая химия поверхностей, пер. с англ., М., 1979; Хейфец Л. И., Неймарк А. В., Многофазные процессы в пористых средах, М., 1982; Аксельруд Г. А., Альтшулер М. А., Введение в капиллярно-химическую технологию, М., 1983. Н. В. Чураев.
Конденсацию паров смачивающей жидкости в капиллярах твердого тела называют капиллярной конденсацией. Пар может конденсироваться лишь при температуре ниже критической. Когда пар над мениском достигает насыщения, начинается конденсация и поры адсорбента заполняются жидкостью. Если образующаяся жидкость хорошо смачивает стенки капилляров, то есть поверхность адсорбента, то в капиллярах образуются вогнутые мениски.
Изотермы сорбции при капиллярной конденсации имеют S -образную форму (рис. 19). Характерные особенности таких изотерм заключаются в том, что вначале на кривой намечается некоторый предел адсорбции (почти горизонтальный участок), но при достижении определенного давления кривая резко идет вверх, что говорит о быстром возрастании количества поглощенного пара в результате капиллярной конденсации. И еще одна особенность состоит в несовпадении изотерм сорбции и десорбции, то есть в наличии сорбционного гистерезиса. Это означает, что одному и тому же давлению пара отвечают разные величины сорбции в зависимости от направления процесса. Явление гистерезиса объясняется главным образом наличием следов воздуха в порах, препятствующего полному смачиванию их стенок, разнообразием формы и радиусов капилляров.

Рис. 19. Изотерма сорбции при капиллярной конденсации (m – масса поглощенных сорбентом паров, р – равновесное давление)
Конденсация пара адсорбата в капиллярах на вогнутой поверхности жидкости (жидкий адсорбат смачивает поверхность капилляра) происходит при давлении пара более низком, чем давление насыщенного пара адсорбата над плоской поверхностью жидкости. Причиной этого является различие гидростатических давлений по обе стороны мениска жидкости.
На искривленной поверхности жидкости возникает так называемое капиллярное давление(рис. 20). Оно равно разности гидростатических давлений между точкой, расположенной в фазе (в данном случае – газ), к которой мениск обращен вогнутой стороной, и точкой, расположенной в фазе (в данном случае – жидкость), к которой мениск обращен выпуклой стороной и определяется уравнением Лапласа для капиллярного давления(43):

Рис. 20. Схема, иллюстрирующая возникновение капиллярного давления, где p2 и p1 – давление в газовой (жидкой) и жидкой фазе соответственно, r – радиус кривизны сферического мениска в капилляре
Пониженное гидростатическое давление жидкости под ее вогнутым мениском приводит к пониженному давлению ее насыщенного пара по сравнению с давлением насыщенного ее пара над плоской поверхностью этой же жидкости.
Связь между радиусом r вогнутого сферического мениска, образовавшегося в капилляре и давлением насыщенного пара рr жидкости над этим мениском дается уравнением Томсона – Кельвина,
где рs – давление насыщенного пара над плоской поверхностью жидкости; σ – поверхностное натяжение жидкости; V – мольный объем жидкости; R – газовая постоянная; Т – абсолютная температура.
Если мениск имеет цилиндрическую форму, уравнение (44) принимает вид
где r – радиус кривизны цилиндрического мениска жидкого адсорбата в капилляре.
Сравнение уравнений (44) и (45) показывает, что давление пара адсорбата над цилиндрическим мениском жидкости всегда больше, чем над сферическим мениском той же жидкости с тем же радиусом, однако оба эти давления больше, чем давление насыщенного пара над плоской поверхностью этой же жидкости. Это соотношение позволяет объяснить капиллярную конденсацию.
Уравнение Томсона – Кельвина является основным при расчетах, связанных с явлениями капиллярной конденсации. Если известны давление насыщенного пара жидкости над плоской поверхностью рs, и радиус капилляров адсорбента, то по уравнению Томсона – Кельвина можно вычислить давление пара р, выше которого в капиллярах начинается конденсация на их цилиндрических стенках (уравнение (45)), а затем десорбция с вогнутого сферического мениска (уравнение (44)).
Уравнение Кельвина описывает изменение давления пара из - за изогнутой поверхности раздела жидкость-пар, таких как поверхности капли. Давление паров при выпуклой криволинейной поверхности выше , чем на плоской поверхности. Уравнение Кельвина зависит от термодинамических принципов и не намекает на специальные свойства материалов. Он также используется для определения размера пор распределения пористой среды с использованием адсорбции порометрии . Уравнение назван в честь Уильяма Томсона , также известный как лорд Кельвин.
содержание
- 1 Формулирование
- 2 История
- 3 кажущийся парадокс
- 4 Смотрите также
- 5 Ссылки
- 6 Дальнейшее чтение
формулировка
Уравнение Кельвина может быть записано в виде
пер п п 0 знак равно 2 γ В м р р T , <\ Displaystyle \ пер <\ гидроразрыва <р><р- <0>>> = <\ гидроразрыва <2 \ гамма-V _ <\ <Текст т>>> <рОТ>>>
где это фактическое давление пара, является давление насыщенного пара , является поверхностным натяжением , является мольным объемом жидкости, является универсальным газовым постоянным , радиус капли, и это температура . п <\ Displaystyle р>
п 0 <\ Displaystyle р- <0>>
γ <\ Displaystyle \ гамма>
В м <\ Displaystyle V _ <\ <Текст т>>>
р <\ Displaystyle R>
р <\ Displaystyle г>
T <\ Displaystyle Т>
- Если кривизна является выпуклой, то , p_<0>>"> п > п 0 <\ Displaystyle р>р- <0>>
р- <0>>"> - Если кривизна является вогнутой, то , (где это давление пара , когда поверхность является плоской) п п 0 <\ Displaystyle р
п 0 <\ Displaystyle р- <0>>
Как увеличивается, уменьшается, и капли растут в объеме жидкости. р <\ Displaystyle г>
п <\ Displaystyle р>
Если мы теперь охладить пар, а затем уменьшается, но точно так же . Это означает , что возрастает , поскольку жидкость охлаждается. Мы можем лечить и приближенно фиксированными, что означает , что критический радиус должен также уменьшить. Дополнительно пар переохлаждается, тем меньше критический радиус становится. В конце концов он получает как малые , как несколько молекул, а жидкость проходит гомогенное зарождение и рост. T <\ Displaystyle Т>
п 0 <\ Displaystyle р- <0>>
п / п 0 <\ Displaystyle р / р- <0>>
γ <\ Displaystyle \ гамма>
В м <\ Displaystyle V _ <\ <Текст т>>>
р <\ Displaystyle г>

Изменение давления пара может быть связано с изменением давления Лапласа . Когда давление Лапласа поднимается в капле, капелька имеет тенденцию к более легко испаряется.
При применении уравнения Кельвина, два случая следует различать: капля жидкости в своей собственной паре приведет к положительно искривленной поверхности жидкости, и пузырек пара в жидкости приведет к отрицательно изогнутой поверхности жидкости.
история
Форма уравнения Кельвина здесь не та форма , в которой она появилась в статье лорда Кельвина 1871. Вывод формы , которая появляется в этой статье из исходного уравнения Кельвина был представлен Робертом фон Гельмгольц (сын немецкого физика Германа фон Гельмгольца ) в его диссертации 1885.
Видимый парадокс
Уравнение аналогично Кельвина может быть получена для растворимости мелких частиц или капель в жидкости, с помощью связи между давлением пара и растворимости, таким образом , уравнение Кельвина относится также к твердым веществам, слегка растворимые в жидкости, а также их растворы если парциальное давление заменяются на растворимости твердого вещества (или второй жидкость) на заданном радиусе, и растворимость в плоской поверхности. Следовательно мелкие частицы (например , мелкие капли), более растворимы , чем более крупные. п <\ Displaystyle р>
р <\ Displaystyle г>
п 0 <\ Displaystyle р- <0>>
Эти результаты привели к проблеме , как новые фазы никогда не может возникнуть из старых. Например, если контейнер заполнен парами воды при слегка ниже давления насыщения внезапно охлаждается, возможно , путем адиабатического расширения, как в камере Вильсона , пар может стать пересыщенный по отношению к жидкой воде. Именно тогда в метастабильном состоянии, и мы можем ожидать конденсации иметь место. Разумный молекулярная модель конденсации , казалось бы , что два или три молекулы водяного пара вместе , чтобы сформировать маленькую капельку, и что это ядро конденсации затем растет за счет аккреции, так как дополнительные молекулы пара , случается, ударил его. Уравнение Кельвина, однако, указывает на то, что крошечные капли , как это ядро, будучи лишь несколько ангстрем в диаметре, будет иметь давление паров , много раз больше , чем в объеме жидкости. Насколько крошечные ядра обеспокоены, пар не будет перенасыщенным вообще. Такие ядра следует немедленно повторно испаряться, и появление новой фазы при равновесном давлении, или даже умеренно выше должно быть невозможно. Таким образом, перенасыщение должно быть в несколько раз выше , чем нормальное значение насыщения для спонтанной нуклеации произойти.
Есть два пути решения этого парадокса. В первую очередь, мы знаем статистическую основу второго закона термодинамики . В любой системе в равновесии, всегда есть колебания вокруг равновесного состояния, и если система содержит несколько молекул, эти колебания могут быть относительно большими. Существует всегда есть шанс , что соответствующее колебание может привести к образованию зародыша новой фазы, даже несмотря на то крошечное ядро можно назвать термодинамически неустойчивы. Шанс на флуктуации электронной -Δ S / K , где Δ S является отклонение энтропии от равновесного значения.
Маловероятно, однако, что новые фазы часто возникают по этому механизму флуктуации и в результате спонтанного зарождения. Расчеты показывают , что шанс, е -Δ S / к , как правило , слишком мало. Более вероятно , что крошечные частицы пыли выступают в качестве ядер в пересыщенных паров или растворов. В камере Вильсона, это кластеры ионов , вызванных попутной высокой энергии частицы , которая действует в качестве центров нуклеации. На самом деле, пары кажутся гораздо менее привередливы , чем решения о роде ядер требуется. Это происходит потому , что жидкость будет конденсироваться практически на любой поверхности, но кристаллизация требует наличия кристаллических граней правильного вида.
Читайте также:



