Движущая сила венозного притока. Закон Бернулли

Добавил пользователь Алексей Ф.
Обновлено: 21.12.2024

Один из способов наблюдения течения жидкости состоит в том, что к жидкости подмешивают алюминиевый порошок и следят при сильном освещении за движением алюминиевых блесток. При этом траектории движения этих частиц будут совпадать с линиями тока.

Линии тока – линии, проведенные так, что касательные к ним совпадают по направлению со скоростями частиц жидкости в соответствующих точках пространства.

Свойства линий тока:

1) Цепочки, которые образует алюминиевый порошок, показывают форму линий тока.

2) Через любую точку жидкости можно провести линию тока.

3) Направление линий тока определяется направлением скорости частиц жидкости в данной точке.

4) Густота линий тока характеризует величину скорости в разных точках пространства текущей жидкости: там, где линии тока расположены гуще, скорость больше; там, где линии тока расположены реже, скорость меньше.

Трубка тока – объем жидкости, ограниченный линиями тока.

Скорости элементов жидкости в каждой точке поверхности трубки направлены по касательной к этой поверхности, поэтому частицы при своем движении не пересекают стенок трубки тока.

Различают два вида движения жидкостей:

движение жидкости, при котором отдельные ее слои скользят друг относительно друга, не перемешиваясь.

Движение жидкости, сопровождающееся перемешиванием ее различных слоев с образованием завихрений.

Примеры: течение воды в спокойных реках,

Примеры: поток быстрых рек, океанские течения.

Для описания движения жидкости обычно пользуются следующим методом: фиксируют скорости различных элементов жидкости в одних и тех же точках пространства. Кинематически описать движение реальных жидкостей достаточно сложно. Примем некоторые допущения для упрощения задачи:

1) Ограничимся рассмотрением ламинарного течения.

2) При описании движения жидкости будем рассматривать идеальные жидкости:

Идеальная жидкость – жидкость, вязкостью и сжимаемостью которой можно пренебречь.

Когда мы говорим, что жидкость несжимаема, то имеем в виду, что она не может быть сжата настолько, чтобы заметно изменился ее объем, но очень малое сжатие, вызывающее появление сил упругости, неизбежно происходит.

Вязкость – свойство жидкости оказывать сопротивление относительному перемещению своих частей. Вязкость обусловлена наличием сил внутреннего трения в жидкости.

3) Будем считать, что движение жидкости стационарное:

Скорости элементов жидкости в различных точках пространства, вообще говоря, различны. Если во всех точках пространства скорости элементов жидкости не меняются со временем, то движение жидкости называется стационарным (установившимся).

При стационарном течении любая частица жидкости проходит данную точку с одним и тем же значением скорости. В другой какой-либо точке скорость частицы будет иной, но также постоянной во времени для всех частиц.

Картина линий тока при стационарном течении остается неизменной. Линии тока в этом случае совпадают с траекториями частиц.

Рассмотрим ламинарное течение идеальной жидкости по трубе переменного сечения. Разобьем жидкость на отдельные трубки тока, настолько тонкие, что в каждом сечении скорости элементов жидкости можно считать одинаковыми.

Рассмотрим два сечения S ₁ и S ₂ . Обозначим через и соответствующие скорости течения жидкости.

За малое время Δ t через первое сечение проходит жидкость, масса которой равна: , а через второе - .

Для несжимаемой жидкости и , так как жидкость не пересекает стенок трубки и не может в ней накапливаться. Следовательно:

–уравнение неразрывности несжимаемой жидкости:

модули скоростей несжимаемой жидкости в двух сечениях трубки тока обратно пропорциональны площадям сечений.

Это уравнение справедливо как для стационарного, так и для нестационарного течения.

Давление внутри неподвижной жидкости передается в любую точку этой жидкости без изменений (закон Паскаля). Выясним распределение давления в движущейся жидкости.

Рассмотрим следующий опыт. Возьмем трубку переменного сечения с небольшими отверстиями в стенке, в которые вставлены открытые сверху измерительные трубки. При стационарном течении жидкость в каждой измерительной трубке поднимается до определенной высоты, отсчитываемой от горизонтального уровня. По высоте столба жидкости можно судить о ее давлении на стенки горизонтальной трубки. Опыт показывает, что в широких местах трубки давление больше, чем в узких. Но, согласно уравнению неразрывности несжимаемой жидкости, чем больше сечение трубки, тем меньше скорость течения жидкости. Следовательно, можно сделать вывод:

Закон Бернулли: при стационарном течении жидкости давление больше в тех местах, где меньше скорость течения, и наоборот, меньше в тех местах, где больше скорость течения.

Объяснить результат эксперимента можно следующим образом. Так как при переходе жидкости с участка трубы с большей площадью сечения, на участок с меньшей площадью сечения скорость течения увеличивается, то жидкость движется с ускорением, направленным по течению. При переходе жидкости из узкой части в широкую, скорость течения уменьшается, жидкость движется с ускорением, направленным против течения. Согласно II закону Ньютона ускорение вызывается силой и совпадает с ней по направлению. Такой силой может быть лишь равнодействующая сил давления окружающей жидкости на поверхность выделенного объема. Сила давления представляет собой силу упругости сжатой жидкости. Таким образом, в широком участке трубы давление жидкости должно быть больше, чем в узком участке трубы.

Установим зависимость давления идеальной жидкости от скорости ее стационарного течения математически. Пусть труба переменного сечения расположена наклонно к горизонту. Система труба-жидкость-Земля является замкнутой и потенциальной. Воспользуемся теоремой об изменении кинетической энергии.

Согласно теореме об изменении потенциальной энергии:

По определению работы:

где - плотность кинетической энергии или динамическое давление (обусловленное );

- плотность потенциальной энергии или гидростатическое давление (обусловленное гравитационного взаимодействия);

- статическое давление (обусловленное упругого взаимодействия)

Согласно уравнению Бернулли: сумма давления и плотностей кинетической и потенциальной энергий при стационарном течении идеальной жидкости остается постоянной для любого сечения потока.

Если труба горизонтальна, то и уравнение примет вид:

Применение уравнения Бернулли:

1) Измерение давления и скорости.

Манометр, обращенный отверстием к потоку, измерит большее давление , чем манометр с отверстием, параллельным линиям тока . Избыток давления получается потому, что частицы жидкости тормозятся перед манометром, вследствие этого давление повышается.

Измерив давление и , можно определить скорость потока:

Эта формула может быть использована для измерения скорости подводной лодки или самолета.

2) Определение скорости истечения жидкостей из отверстия в сосуде.

С помощью уравнения Бернулли можно найти скорость истечения идеальной жидкости из отверстия расположенного в сосуде на глубине h относительно поверхности жидкости. Если сосуд широкий, а отверстие мало, то скорости жидкости в сосуде малы. Ко всему потоку жидкости в целом можно применить уравнение Бернулли. В верхнем сечении у поверхности давление равно атмосферному, а скорость . В нижнем сечении трубки – в отверстии давление также равно атмосферному. Если скорость в отверстии обозначить через , то из уравнения Бернулли для этих двух сечений получим:

Истечение идеальной жидкости происходит с той же скоростью, какую имело бы тело при свободном падении с высоты h .

Применение уравнения Бернулли в технике:

1) Водоструйный насос.

2) Пульверизатор.

Простейший пульверизатор состоит из двух трубок, расположенных перпендикулярно друг другу. Через горизонтальную трубку продувается воздух. В узкой части струи при выходе из трубки давление меньше атмосферного. Атмосферное давление поднимает жидкость по вертикальной трубке, и она распыляется струей воздуха.

3) Карбюратор – прибор, предназначенный для питания двигателя внутреннего сгорания горючей смесью.

Во время всасывающих тактов движения поршня двигателя наружный воздух проходит по трубе, которая имеет суженную часть – диффузор. В диффузоре помещен жиклер (распылитель воздуха) – трубка с малым отверстием. Жиклер соединен с поплавковой камерой карбюратора. При прохождении потока воздуха его скорость в диффузоре резко возрастает, давление становится меньше атмосферного и атмосферное давление выталкивает бензин из поплавковой камеры через жиклер. Бензин распыляется в потоке воздуха – образуется рабочая смесь, которая поступает в цилиндр двигателя.

Жидкости и газы существенно отличаются друг от друга. Различие между жидкостями и газами обусловлено большой сжимаемостью газов. Несмотря на это, явления в неподвижных жидкостях и газах аналогичны (закон Паскаля, закон Архимеда). При исследовании движения в жидкостях и газах эта аналогия во многом сохраняется, а именно: при движении газов со скоростями, значительно меньшими скорости звука (340м/с), сжимаемость газов достаточно мала и ее можно не учитывать. В связи с этим полученные ранее законы и утверждения можно применять и для газов.

Применим уравнение Бернулли для расчета подъемной силы крыла самолета.

При отсутствии сил сопротивления воздуха крыло обтекает ламинарный поток. Согласно уравнению Бернулли:

Если учитывать сопротивление воздуха, картина будет другая. Когда воздушный поток начинает обтекать крыло, то из-за действия сил трения у задней кромки образуется вихрь, в котором воздух вращается против часовой стрелки, если крыло движется влево. Применим уравнение Бернулли:

(т.к. вблизи точки 2 образуется вихрь) и .

Но по закону сохранения момента импульса при возникновении вращения против часовой стрелки должно возникнуть вращение по часовой стрелке.

Такое вращение воздуха и возникает вокруг крыла. На обтекающий крыло поток накладывается циркуляция воздуха вокруг крыла. В результате скорость воздушного потока над крылом оказывается больше, чем под крылом, так как над крылом скорость циркуляции имеет такое же направление, как и скорость набегающего на крыло потока, а под крылом эти скорости противоположны по направлению. Но согласно закону Бернулли давление должно быть больше там, где скорость меньше. Следовательно, под крылом самолета давление больше, чем над ним. Из-за этого и возникает подъемная сила.

Известно, что наименьшая сила сопротивления действует на тело каплеобразной формы. Такая форма крыла самолета обеспечивает хорошую его обтекаемость.

"Применим ли закон Бернулли для движения крови по кровеносным сосудам?"

Работа Антроповой Д.А. помогает найти ответ на проблемный вопрос, возникший при попытке применить законы физики к физиологии человека.

Идея работы: объяснить с помощью законов физики движение крови по кровеносным сосудам. Экспериментально доказать, что давление и скорость движения крови в сосудах зависят от площади сечения. Создать модель, которая поможет продемонстрировать эту зависимость. Проверить и объяснить на эксперименте, применим ли закон Бернулли для движения крови по кровеносным сосудам.

Вложение	Размер
"Применим ли закон Бернулли для движения крови по кровеносным сосудам?"	904.34 КБ

Предварительный просмотр:

Частное общеобразовательное учреждение «Школа-интернат №22 ОАО «РЖД»

"Применим ли закон Бернулли для движения крови по кровеносным сосудам?"

Автор: Антропова Дарья Андреевна,

10 класс, Школа интернат № 22 ОАО "РЖД"

Научные руководители: Хамаганова Татьяна Фёдоровна,

учитель химии и биологии высшей квалификационной категории,

Школа-интернат №22 ОАО «РЖД»

Максимова Александра Андреевна,

учитель физики 1 квалификационной категории,

Виды кровеносных сосудов, их основные характеристики……….………………..

Физико-биологическое моделирование движения крови по сосудам и возможность применения к ней закона Бернулли.………….………………………..

Анализ полученных данных в результате исследовательской работы ……….……

Список использованных источников………………………………………………………

С точки зрения биологии, движение крови по кровеносным сосудом, это процесс довольно сложный и характеризуется множеством параметров, такими как скорость течения, диаметр сосуда, вязкость крови и т.д. Но возможно ли применить физические законы к этому процессу. Возникнут ли противоречия при попытке применить законы физики к физиологии человека.

Так, в гемодинамике [1] , движение крови по сосудам объясняется такими физическими величинами как давление и скорость движения крови. В гидродинамике данные величины связаны законом Бернулли. Но применим данный закон к движению крови.

Цель эксперимента : выявить зависимость внутреннего давления и скорости движения жидкости от площади поперечного сечения кровеносных сосудов.

Гипотеза: закон Бернулли применим для движения крови по кровеносным сосудам.

Идея проекта: объяснить с помощью законов физики движение крови по кровеносным сосудам. Экспериментально доказать, что давление и скорость движения крови в сосудах зависят от площади сечения. Создать модель, которая поможет продемонстрировать эту зависимость. Проверить и объяснить на эксперименте, применим ли закон Бернулли для движения крови по кровеносным сосудам.

Объект исследования: движение крови по кровеносным сосудам.

Предмет исследования: давление и скорость течения крови.

изучить литературу по данной теме;
рассмотреть закономерности в уравнение Бернулли и гемодинамике;
создать физико-биологическую модель кровеносных сосудов;
сравнить и проанализировать полученные данные.

Метода исследования : практический эксперимент, посредством моделирования, мыслительно-логические методы, такие как постановка проблемы, сравнение и анализ.

1. Виды кровеносных сосудов, их основные характеристики

Кровообращение — циркуляция крови по организму. Начиная с представителей класса рыб, кровь приводится в движение сокращениями сердца и циркулирует по сосудам. Кровь снабжает ткани организма кислородом, питательными веществами, гормонами и доставляет продукты обмена веществ к органам их выделения. Обогащение крови кислородом происходит в лёгких, а насыщение питательными веществами — в органах пищеварения. Кровообращение регулируется гормонами и вегетативной нервной системой. Различают малый (через лёгкие) и большой (через органы и ткани) круги кровообращения.

Кровообращение — важный фактор в жизнедеятельности организма человека и ряда животных. Кровь может выполнять свои разнообразные функции только находясь в постоянном движении.

Кровеносная система человека и многих животных состоит из сердца и сосудов, по которым кровь движется к тканям и органам, а затем возвращается в сердце. Крупные сосуды, по которым кровь движется к органам и тканям, называются артериями. Артерии разветвляются на более мелкие артерии, артериолы, и, наконец, на капилляры. По сосудам, называемым венами, кровь возвращается в сердце. Сердце четырёхкамерное и имеет два круга кровообращения.

Рис.1 Круги кровообращения

Самые первые количественные измерения механических явлений в кровообращении были сделаны Стивеном Хейлзом (1677—1761 г.), который измерил артериальное и венозное кровяное давление, объём отдельных камер сердца и скорость вытекания крови из нескольких вен и артерий, продемонстрировав таким образом, что большая часть сопротивления течению крови приходится на область микроциркуляции.[1] Он полагал, что вследствие упругости артерий течение крови в венах более или менее установившееся, а не пульсирующее, как в артериях.

Кровообращение человека происходит по трём группам сосудов: артерии, капилляры и вены. Рассмотрим их основные отличительные характеристики.

Основные характеристики сосудов человека:

Артерии, которые почти не содержат гладких мышц, но имеют мощную эластическую оболочку, выполняют главным образом «буферную» роль, сглаживая перепады давлений между систолой и диастолой. Именно растяжение стенки сосуда воспринимается как удар пульса. Артериолы обладают развитой гладкой мускулатурой, благодаря которой способны активно менять свой просвет и, таким образом, регулировать сопротивление кровотоку.

Марчелло Мальпиги, который в 1661 г. открыл капилляры — звено кровеносных сосудов, которое соединяет артерии и вены, — и таким образом завершил описание замкнутой сосудистой системы.[2]

Капилляры характеризуются тем, что их сосудистая стенка представлена одним слоем клеток, так что они высоко проницаемы для всех растворенных в плазме крови низкомолекулярных веществ. Здесь происходит обмен веществ между тканевой жидкостью и плазмой крови.

От органов кровь возвращается через посткапилляры в венулы и вены в правое предсердие по верхней и нижней полым венам, а также по коронарным венам. Гладкие мышцы вен обеспечивают изменение их объёма в весьма широких пределах, приспосабливая их ёмкость к меняющемуся объёму циркулирующей крови. поэтому физиологическая роль вен определяется как «ёмкостные сосуды».

Движение крови по сосудам осуществляется, главным образом, благодаря разности давлений между артериальной системой и венозной. Это утверждение полностью справедливо для артерий и артериол, в капиллярах и венах появляются вспомогательные механизмы. Разность давлений создаётся ритмической работой сердца, перекачивающего кровь из вен в артерии. [3]

2. Закон Бернулли

Закон Бернулли [4] (также уравнение Бернулли, теорема Бернуллиили интеграл Бернулли) устанавливает зависимость между скоростью стационарного потока жидкости и её давлением.

При переходе жидкости с участка трубки с большим сечением на участок с меньшим сечением, скорость течение возрастает. Т.е. жидкость движется с ускорением. Следовательно, на жидкость действует сила. В горизонтальной трубе эта сила может возникнуть только из-за разности давлений в широком и узком участках трубы. Давление в широком участке трубы должно быть больше чем в узком участке.

Математический вид закона Бернулли выглядит следующим образом:

ρ— плотность жидкости;

υ— скорость потока;

g — ускорение свободного падения [5].

Согласно этому закону, если вдоль линии тока давление жидкости возрастает, то скорость течения убывает, и наоборот.

3. Физико-биологическое моделирование движения крови по сосудам и возможность применения к ней закона Бернулли

Для того, чтобы наглядно продемонстрировать движение крови, я создала модель, состоящую из трубок разного диаметра, где трубка с наименьшим поперечным сечением будет демонстрировать движение крови в капиллярах. А трубка с наибольшим поперечным сечением – движение в аорте. Трубка среднего диаметра – движение в артериях. И к каждой трубке подсоединён жидкостный манометр. Подключаем нашу установку к водопроводной сети под давлением, и проверяем жидкостным манометром давление, создаваемое в трубках разного диаметра.

Для создания модели нам понадобились:

3 трубки различного сечения, для демонстрации движения крови в сосудах разного диаметра (аорта, артерии, капилляры);
3 манометра, для определения внутреннего давления жидкости в трубке;
подводящие и отводящие жидкость шланги и переходники;
стробоскоп, для наблюдения быстрого движения струящейся жидкости из трубки;
пищевой краситель красного цвета, для демонстрации скорости движения жидкости в трубке.

Рис. 2 Экспериментальная модель кровеносных сосудов

В трубке с наибольшим поперечным сечением манометр показывает 240 мм рт.ст. В трубке с наименьшим поперечным сечением 217 мм рт. ст.. В трубке среднего диаметра - 210 мм. рт. ст. Убираем манометры. Снова подключаем нашу установку к водопроводной сети. И сравниваем высоту фонтанов.

Рис. 3 Разность высот «фонтанов»

Фонтан, образующийся на трубке большего диаметра самый высокий, а самый низкий на трубке меньшего диаметра. Оказалось, что вода быстрее окрашивается в трубке меньшего диаметра.

4. Анализ полученных данных в результате исследовательской работы

Т.к. вода быстрее окрашивается в трубке меньшего диаметра, следовательно, скорость движения воды в ней самая высокая, что противоречит движению крови по кровеносным сосудам. Ведь в капиллярах скорость движения крови меньше, чем артериях, хотя артерии шире. А это имеет огромный биологический смысл, ведь благодаря медленному движению крови по капиллярам в тканях осуществляется газообмен.

Разрешить проблему и разобраться в данном вопросе мне помогла формула Торричелли, не входящая в школьный курс.

- скорость кровотока в сосуде,

S - поперечное сечение кровеносного сосуда.

Данная формула показывает, что линейная скорость кровотока уменьшается по мере увеличения суммарного сечения параллельно соединённых сосудов, т.е. учитывается свойство пропускной способности сосудов . Есть закономерность: циркуляция жидкости выше в том участке, где имеется наименьшее сечение сосуда. Такой участок — аорта. Самый широкий суммарный просвет в капиллярах. Исходя из этого, максимальная скорость в аорте (500 мм/сек), минимальная – в капиллярах (0.5 мм/сек) [6].

Наша гипотеза подтвердилась: уравнение Бернулли применимо к движению крови по кровеносным сосудам. Возникшее противоречие объясняется тем, что в капиллярах скорость движения крови низкая, потому что в капиллярах нашего тела самый широкий суммарный просвет, т.е. суммарная площадь сечения, которая в 1000 раз больше сечения аорты, и приводит к минимальной скорости движения крови в капиллярах.

Проведенные исследования важны с практической точки зрения. Данная модель может быть использована на уроках физики при углублённом изучении гидродинамики, а также на уроках биологии при рассмотрении кровеносной системы человека

Движущая сила венозного притока. Закон Бернулли

Факторы влияющие на величину венозного притока. Зависимость венозного притока

Величина венозного притока является функцией двух величин — градиента среднего системного давления и давления в правом предсердии, а также сопротивления кровотоку на пути движения крови к правому предсердию. Эта функция описывается следующим уравнением:

V = Ps-Pp/R, где
V — объем притекающей в правое предсердие крови;
Ps — среднее системное давление в сердечно-сосудистой системе;
Рр — давление в правом предсердии;
R — общее сопротивление кровотоку по артериальному и венозному руслу.

Нетрудно заметить, что числитель этой формулы представляет градиент среднего системного давления и давления в правом предсердии, а знаменатель — сопротивление кровотоку, зависящий от ряда факторов: сосудистого тонуса, реологических свойств (вязкость) крови, а также от внесосудистых (сдавливание крупных вен) и внутрисосудистых (венозные тромбозы) факторов.
Рассмотрим влияние некоторых из этих факторов на величину венозного притока.

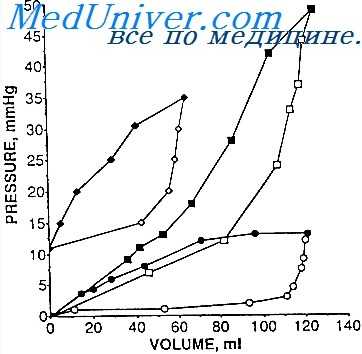
Выше было отмечено, что градиент давлений правого предсердия и среднего системного давления зависит от двух величин — емкости сосудистого русла и присасывающей силы грудной клетки. Следовательно, такие факторы, как объем циркулирующей крови, тонус сосудов венозного и артериального русла, биомеханика респираторной системы и являются факторами, определяющими градиент давлений.

Не меньшее влияние на величину венозного притока оказывает периферическое сопротивление. Величина венозного притока обратно пропорциональна уровню периферического сопротивления (знаменатель приведенной выше формулы). На рисунке приведены кривые венозного притока при изменяющемся уровне периферического сопротивления.

Отсюда следует, чем выше периферическое сопротивление в сосудистой системе, тем большее среднее системное давление необходимо для продвижения одного и того же объема крови к правому предсердию. Однако при прочих равных условиях (при стабильном уровне периферического сопротивления) увеличение системного давления сопровождается увеличением венозного притока.

На диаграмме отчетливо видно, что чем выше среднее системное давление, тем больше оно разнится с давлением в предсердии (больше градиент) и тем больше венозный приток. Так, при давлении в правом предсердии, равном 2 мм Нд и при нормальном Pms, равном 7 мм Нд, максимальный венозный приток составит 6 л/мин (красная кривая), при Pms равном 14 мм Нд, — 11 л/мин (синяя кривая), при Pms, равном 3,5 мм Нд, — только 3,7 л/мин (зеленая кривая).

На величину среднего системного давления могут влиять такие синдромы, как артериальная и венозная гипотония, гиповолемия, изменение количества внесосудистой жидкости, внутрибрюшная гипертензия, нарушение герметичности грудной клетки, компрессия сосудов сокращающейся мускулатурой или объемными процессами (опухоль, гематома и др.).

На уменьшение периферического сопротивления могут влиять расширение периферических сосудов (гипоксемия, раскрытие артерио-венозных шунтов), снижение вязкости крови (гемодилюция, применение антикоагулянтов, дезагрегантов), преобладание вазодилятации преимущественно в артериальном русле (применение симпатолических веществ).

Информация на сайте подлежит консультации лечащим врачом и не заменяет очной консультации с ним.
См. подробнее в пользовательском соглашении.

Движение жидкости в замкнутой системе подчиняется закону Бернул-ли, который определяет, что жидкость перемещается из области более высокого давления в область более низкого давления. Исходя из этого, можно заключить, что движущей силой венозного притока является градиент среднего системного давления и давления в правом предсердии.

В физиологии кровообращения под средним системным давлением в сердечно-сосудистой системе понимается давление, которое устанавливается в условиях прекращения кровотока (остановка сердечной деятельности), после того, как перераспределение крови между артериями, капиллярами и венами приведет к выравниванию давления во всех сегментах соответствующего круга кровообращения. Иначе говоря, среднее системное давление отражает усредненный уровень давлений во всех сегментах сердечно-сосудистой системы.

Величина среднего давления в каждом сегменте сердечно-сосудистой системы зависит от его емкости, под которой понимается объем крови, находящейся в этом сегмент при данном уровне давления и описывается следующим отношением:
С = V/P, где
С — емкость сосудистого русла;
V — изменение объема крови;
Р — изменение давления.

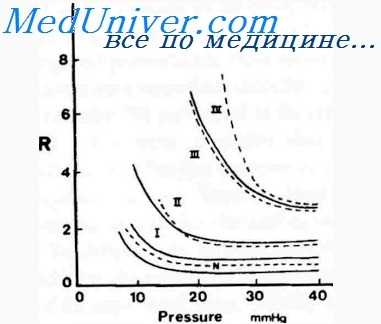
Отсюда следует, что при изменении емкости сосудистого русла будет изменяться и среднее системное давление. Чем больше емкость сосудистого русла, тем меньше будет возрастать системное давление при увеличении в нем объема крови. Специальными исследованиями было установлено, что емкость венозного русла в 18 раз больше артериального.

Поэтому венозное русло может депонировать значительные количества крови без существенного повышения в нем давления, а даже незначительный прирост объема крови в артериальной системе неизбежно приведет к возрастанию системного давления. Следовательно, среднее системное давление в сердечно-сосудистой системе представляет собой усредненную величину емкости артериального и венозного русла.

К сожалению, определить среднее системное давление можно только в эксперименте, т.к. для этого необходима остановка сердца. Однако известно, что основные гемодинамические функции у животного (собаки) и человека существенно не различаются и закономерности, установленные в эксперименте, подтверждаются при исследованиях, проведенных у человека при операциях на сердце в условиях искусственного кровообращения.
В связи с этим данные, полученные в эксперименте, в частности относительно закономерностей венозного притока, могут быть с достаточной степенью вероятности экстраполированы на человека.

Так было установлено, что нормальные величины среднего системного давления в большом и малом круге кровообращения различаются незначительно и составляют соответственно 7 мм Нд для большого и 5 мм Нд для малого круга кровообращения. Следовательно, в нормальных условиях (при отсутствии патологии гемодинамики) градиент давлений, обеспечивающий венозный приток, составляет 7-10 мм Нд. И именно в этом диапазоне давлений реализуются нормальный венозный приток и сердечный выброс.

Комплексные влияния на венозный приток. Влияние периферического сопротивления на венозный приток

В практической работе нередко встречаются ситуации, когда на венозный приток влияют одновременно оба фактора — изменения системного давления и периферического сопротивления. Такую ситуацию мы наблюдали в хирургии легких при острой массивной кровопотере.

В этих случаях снижение объема циркулирующей крови уменьшало системное давление, а торакотомия, увеличивая давление в плевральной полости и снижая присасывающую силу грудной клетки, обусловливала повышение давления в правом предсердии.

Все это приводило к уменьшению градиента системного давления и давления в правом предсердии, а, следовательно, к снижению венозного притока. К негативному влиянию этих факторов присоединялось повышение сопротивления кровотоку, особенно при правосторонних операциях, при которых повышение внутриплеврального давления и манипуляции хирурга создавали препятствие кровотоку по верхней полой вене.
Влияние различных комбинаций факторов, обеспечивающих венозный приток, иллюстрируют результаты экспериментальных исследований, проведенных в лаборатории А. Гайтона.

Материалы, приведенные на графиках, свидетельствуют, что наиболее неблагоприятные условия для венозного притока возникают при увеличении периферического сопротивления. Несмотря на то, что среднее системное давление достаточно велико (10,5 мм Нд), оно не может преодолеть удвоенное сопротивление, в связи с чем венозный приток существенно сокращается (цифра 3).

Противоположная картина наблюдается при снижении сопротивления в 2 раза. При примерно аналогичном системном давлении венозный приток увеличится более чем в 3 раза (цифра 2). При сниженном периферическом сопротивлении примерно на 60%, нормальный или даже несколько увеличенный венозный приток реализуется при вдвое сниженном системном давлении (цифра 4).

Учитывая эти данные, можно придти к заключению, что наибольшее влияние на регуляцию венозного притока оказывает периферическое сопротивление кровотоку. И тем не менее, в рутинной практике реаниматологу проще регулировать венозный приток путем воздействия на системное давление (инфузионная терапия), чем на периферическое сопротивление, поскольку имеющиеся в распоряжении реаниматолога, методы регуляции периферического сопротивления (применение реологически активных средств, препаратов с адренэргическими эффектами) менее управляемы, чем инфузионная терапия.

Однако в практике интенсивной терапии критических состояний нередко возникают ситуации, когда необходимо регулировать и периферическое сопротивление (тяжелые гипертонические кризы, шоковые синдромы и др.).

Читайте также: