Теория эктопических центров. Теория круговой волны
Добавил пользователь Валентин П. Обновлено: 28.01.2026
До сих пор мы занимались геометрической оптикой и изучали распространение световых лучей. При этом понятие луча мы считали интуитивно ясным и не давали ему определения. Основные законы геометрической оптики были сформулированы нами как постулаты.
Теперь мы займёмся волновой оптикой, в которой свет рассматривается как электромагнитные волны. В рамках волновой оптики понятие луча уже можно строго определить. Базовым постулатом волновой теории является принцип Гюйгенса; законы геометрической оптики оказываются его следствиями.
Волновые поверхности и лучи.
Представьте себе маленькую лампочку, которая даёт частые периодические вспышки. Каждая вспышка порождает расходящуюся световую волну в виде расширяющейся сферы (с центром в лампочке). Остановим время - и увидим в пространстве остановившиеся световые сферы, образованные вспышками в различные предшествующие моменты времени.
Эти сферы - так называемые волновые поверхности. Заметьте, что лучи, идущие от лампочки, перпендикулярны волновым поверхностям.
Чтобы дать строгое определение волновой поверхности, давайте вспомним сначала, что такое фаза колебаний. Пусть величина совершает гармонические колебания по закону:
Так вот, фаза - это величина , которая является аргументом косинуса. Фаза, как видим, линейно возрастает со временем. Значение фазы при равно и называется
начальной фазой.
Вспомним также, что волна представляет собой распространение колебаний в пространстве.В случае механических волн это будут колебания частиц упругой среды, в случае электромагнитных волн - колебания векторов напряжённости электрического поля и индукции магнитного поля.
Вне зависимости от того, какие волны рассматриваются, мы можем сказать, что в каждой точке пространства, захваченной волновым процессом, происходят колебания некоторой величины; такой величиной является набор координат колеблющейся частицы в случае механической волны или набор координат векторов, описывающих электрическое и магнитное поля в электромагнитной волне.
Фазы колебаний в двух различных точках пространства, вообще говоря, имеют разное значение. Интерес представляют множества точек, в которых фаза одна и та же. Оказывается, совокупность точек, в которых фаза колебаний в данный момент времени имеет фиксированное значение, образует двумерную поверхность в пространстве.
Определение. Волновая поверхность - это множество всех точек пространства, в которых фаза колебаний в данный момент времени имеет одно и то же значение.
Коротко говоря, волновая поверхность есть поверхность постоянной фазы. Каждому значению фазы отвечает своя волновая поверхность. Набору различных значений фазы соответствует семейство волновых поверхностей.
С течением времени фаза в каждой точке меняется, и волновая поверхность, отвечающая фиксированному значению фазы, перемещается в пространстве. Следовательно, распространение волн можно рассматривать как движение волновых поверхностей! Тем самым в нашем распоряжении оказываются удобные геометрические образы для описания физических волновых процессов.
Например, если точечный источник света находится в прозрачной однородной среде, то волновые поверхности являются концентрическими сферами с общим центром в источнике. Распространение света выглядит как расширение этих сфер. Мы это уже видели выше в ситуации с лампочкой.
Через каждую точку пространства в данный момент времени может проходить только одна волновая поверхность. В самом деле, если предположить, что через точку проходят две волновых поверхности, отвечающие различным значениям фазы и , то немедленно получим противоречие: фаза колебаний в точке окажется одновременно равна этим двум различным числам.
Коль скоро через точку проходит единственная волновая поверхность, то однозначно определено и направление перпендикуляра к волновой поверхности в данной точке.
Определение. Луч - это линия в пространстве, которая в каждой своей точке перпендикулярна волновой поверхности, проходящей через эту точку.
Иными словами, луч есть общий перпендикуляр к семейству волновых поверхностей. Направление луча - это направление распространения волны. Вдоль лучей осуществляется перенос энергии волны от одних точек пространства к другим.
По мере распространения волны происходит перемещение границы, которая разделяет область пространства, захваченную волновым процессом, и невозмущённую пока область. Эта граница называется волновым фронтом. Таким образом, волновой фронт - это множество всех точек пространства, которых достиг колебательный процесс в данный момент времени. Волновой фронт есть частный случай волновой поверхности; это, если можно так выразиться, "самая первая" волновая поверхность.
К наиболее простым видам геометрических поверхностей относятся сфера и плоскость. Соответственно, имеем два важных случая волновых процессов с волновыми поверхностями такой формы - это сферические и плоские волны.
Сферическая волна.
Волна называется сферической, если её волновые поверхности - сферы (рис. 1 ).
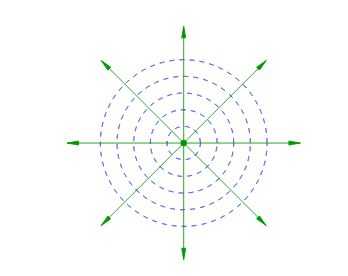 |
| Рис. 1. Сферическая волна |
Волновые поверхности показаны синим пунктиром, а зелёные радиальные стрелки - это лучи, перпендикулярные волновым поверхностям.
Рассмотрим прозрачную однородную среду, физические свойства которой одинаковы вдоль всех направлений. Точечный источник света, помещённый в такую среду, излучает сферические волны. Это понятно -
ведь свет пойдёт в каждом направлении с одинаковой скоростью, так что любая волновая поверхность будет сферой.
Ну а световые лучи, как мы заметили, оказываются в этом случае обычными прямолинейными геометрическими лучами с началом в источнике. Помните закон прямолинейного распространения света: в прозрачной однородной среде световые лучи являются прямыми линиями? В геометрической оптике мы сформулировали его как постулат. Теперь мы видим (для случая точечного источника), как этот закон следует из представлений о волновой природе света.
В теме "Электромагнитные волны" мы ввели понятие плотности потока излучения:
Здесь - энергия, которая переносится за время через поверхность площади , расположенную перпендикулярно лучам. Таким образом, плотность потока излучения - это энергия, переносимая волной вдоль лучей через единицу площади в единицу времени.
В нашем случае энергия равномерно распределяется по поверхности сферы, радиус которой увеличивается в процессе распространения волны. Площадь поверхности сферы равна: , поэтому для плотности потока излучения получим:
Как видим, плотность потока излучения в сферической волне обратно пропорциональна квадрату расстояния до источника.
Поскольку энергия пропорциональна квадрату амплитуды колебаний электромагнитного поля, мы приходим к выводу, что амплитуда колебаний в сферической волне обратно пропорциональна расстоянию до источника.
Плоская волна.
Волна называется плоской, если её волновые поверхности - плоскости (рис. 2 ).
 |
| Рис. 2. Плоская волна |
Синим пунктиром показаны параллельные плоскости, являющиеся волновыми поверхностями. Лучи - зелёные стрелки - снова оказываются прямыми линиями.
Плоская волна - одна из важнейших идеализаций волновой теории; математически она описывается наиболее просто. Этой идеализацией можно пользоваться, например, когда мы находимся на достаточно большом расстоянии от источника. Тогда в окрестности точки наблюдения можно пренебречь искривлением сферической волновой поверхности и считать волну приблизительно плоской.
В дальнейшем, выводя законы отражения и преломления из принципа Гюйгенса, мы будем использовать именно плоские волны. Но сначала разберёмся с самим принципом Гюйгенса.
Принцип Гюйгенса.
Мы говорили выше, что распространение волн удобно представлять себе как движение волновых поверхностей. Но согласно каким правилам перемещаются волновые поверхности? Иными словами - как, зная положение волновой поверхности в данный момент времени, определить её положение в следующий момент?
Ответ на этот вопрос даёт принцип Гюйгенса - основной постулат волновой теории. Принцип Гюйгенса равным образом справедлив как для механических, так и для электромагнитных волн.
Чтобы лучше понять идею Гюйгенса, давайте рассмотрим такой пример. Бросим в воду горсть камней. От каждого камня пойдёт круговая волна с центром в точке падения камня. Эти круговые волны, накладываясь друг на друга, создадут общую волновую картину на поверхности воды. Важно то, что все круговые волны и порождённая ими волновая картина будут существовать и после того, как камни пустятся на дно. Стало быть, непосредственной причиной исходных круговых волн служат не сами камни, а локальные возмущения поверхности воды в тех местах, куда камни упали. Именно локальные возмущения сами по себе являются источниками расходящихся круговых волн и формирующейся волновой картины, и уже не столь важно, что конкретно послужило причиной каждого из этих возмущений - камень ли, поплавок или какой-то иной объект. Для описания последующего волнового процесса важно только то, что в определённых точках поверхности воды возникли круговые волны.
Ключевая идея Гюйгенса состояла в том, что локальные возмущения могут порождаться не только посторонними объектами типа камня или поплавка, но также и распространяющейся в пространстве волной!
Принцип Гюйгенса. Каждая точка пространства, вовлечённая в волновой процесс, сама становится источником сферических волн.
Эти сферические волны, распространяющиеся во все стороны от каждой точки волнового возмущения, называются вторичными волнами. Последующая эволюция волнового процесса состоит в наложении вторичных волн, испущенных всеми точками, до которых волновой процесс уже успел добраться.
Принцип Гюйгенса даёт рецепт построения волновой поверхности в момент времени по известному её положению в момент времени (рис. 3 ).
| Рис. 3. Принцип Гюйгенса: движение волновых поверхностей |
Именно, каждую точку исходной волновой поверхности мы рассматриваем как источник вторичных волн. За время вторичные волны пройдут расстояние , где - скорость волны. Из каждой точки старой волновой поверхности строим сферы радиуса ; новая волновая поверхность будет касательной ко всем этим сферам. Говорят ещё, что волновая поверхность в любой момент времени служит огибающей семейства вторичных волн.
Но, конечно, для построения волновой поверхности мы не обязаны брать вторичные волны, испущенные точками, лежащими непременно на одной из предыдущих волновых поверхностей.Искомая волновая поверхность будет огибающей семейства вторичных волн, излучённых точками вообще всякой поверхности, вовлечённой в колебательный процесс.
На базе принципа Гюйгенса можно вывести законы отражения и преломления света, которые раньше мы рассматривали лишь как обобщение экспериментальных фактов.
Вывод закона отражения.
Предположим, что на поверхность раздела двух сред падает плоская волна (рис. 4 ). Фиксируем две точки этой поверхности.
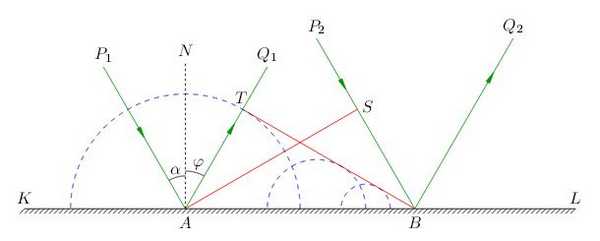 |
| Рис. 4. Отражение волны |
В эти точки приходят два падающих луча и ; плоскость , перпендикулярная этим лучам, есть волновая поверхность падающей волны.
В точке проведена нормаль к отражающей поверхности. Угол есть, как вы помните, угол падения.
Из точек И выходят отражённые лучи и . Перпендикулярная этим лучам плоскость есть волновая поверхность отражённой волны. Угол отражения обозначим пока ; мы хотим доказать, что .
Все точки отрезка служат источниками вторичных волн. Раньше всего волновая поверхность приходит в точку . Затем, по мере движения падающей волны, в колебательный процесс вовлекаются другие точки данного отрезка, и в самую последнюю очередь - точка .
Соответственно, раньше всего начинается излучение вторичных волн в точке ; сферическая волна с центром в имеет на рис. 4 наибольший радиус. По мере приближения к точке радиусы сферических вторичных волн, испущенных промежуточными точками, уменьшаются до нуля - ведь вторичная волна будет излучена тем позже, чем ближе её источник находится к точке .
Волновая поверхность отражённой волны есть плоскость, касательная ко всем этим сферам. На нашем планиметрическом чертеже есть отрезок касательной, проведённой из точки к самой большой окружности с центром в и радиусом .
Теперь заметим, что радиус - это расстояние, пройденное вторичной волной с центром в за то время, пока волновая поверхность двигается к точке . Скажем это чуть по-другому: время движения вторичной волны от точки до точки равно времени движения падающей волны от точки до точки . Но скорости движения падающей и вторичной волн совпадают - ведь дело происходит в одной и той же среде! Поэтому, раз совпадают скорости и времена, то равны и расстояния: .
Получается, что прямоугольные треугольники и равны по гипотенузе и катету. Стало быть, равны и соответствующие острые углы: . Остаётся заметить, что (так как оба они равны ) и (оба они равны ).
Таким образом, - угол отражения равен углу падения, что и требовалось.
Кроме того, из построения на рис. 4 нетрудно видеть, что выполнено и второе утверждение закона преломления: падающий луч , отражённый луч и нормаль к отражающей поверхности лежат в одной плоскости.
Вывод закона преломления.
Теперь покажем, как из принципа Гюйгенса следует закон преломления. Будем для определённости считать, что плоская электромагнитная волна распространяется в воздухе и падает на границу с некоторой прозрачной средой (рис. 5 ). Как обычно, угол падения есть угол между падающим лучом и нормалью к поверхности, угол преломления - это угол между преломлённым лучом и нормалью.
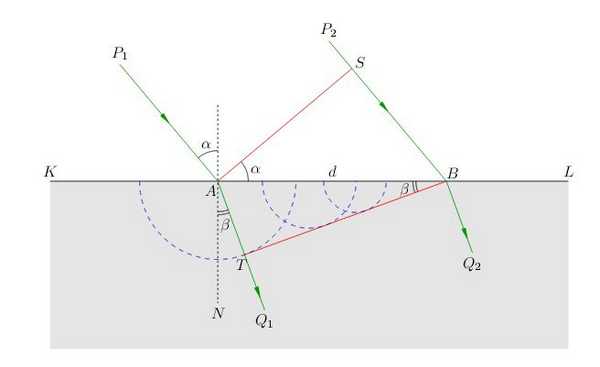 |
| Рис. 5. Преломление волны |
Точка является первой точкой отрезка , которой достигает волновая поверхность падающей волны; в точке излучение вторичных волн начинается раньше всего. Пусть - время, которое с этого момента требуется падающей волне, чтобы достичь точки , то есть пройти отрезок .
Скорость света в воздухе обозначим , скорость света в среде пусть будет . Пока падающая волна проходит расстояние и достигает точки , вторичная волна из точки распространится на расстояние .
Поскольку , то . Вследствие этого волновая поверхность не параллельна волновой поверхности - происходит преломление света! В рамках геометрической оптики не давалось никакого объяснения того, почему вообще наблюдается явление преломления. Причина преломления кроется в волновой природе света и становится понятной с точки зрения
принципа Гюйгенса: всё дело в том, что скорость вторичных волн в среде меньше скорости света в воздухе, и это приводит к повороту волновой поверхности относительно исходного положения .
Из прямоугольных треугольников и легко видеть, что и (для краткости обозначено ). Имеем, таким образом:
Поделив эти уравнения друг на друга, получим:
Отношение синуса угла падения к синусу угла преломления оказалось равно постоянной величине , не зависящей от угла падения. Эта величина называется показателем преломления среды:
Получился хорошо известный нам закон преломления:
Обратите внимание: физический смысл показателя преломления (как отношения скоростей света в вакууме и в среде) прояснился опять-таки благодаря принципу Гюйгенса.
Из рис. 5 очевидно и второе утверждение закона преломления: падающий луч , преломлённый луч и нормаль к границе раздела лежат в одной плоскости.
Теории периферического анализа звука
Звук - это волнообразное движение частиц воздуха.
Слух - способность биологических организмов воспринимать звуки органами слуха; специальная функция слухового аппарата, возбуждаемая звуковыми колебаниями окружающей среды, например, воздуха или воды.
Основные функции звукового анализатора - звукопроведение и звуковосприятие.
Звукопроведение - это процесс доставки звуковой энергии к рецепторному аппарату.
Звуковосприятие - это процесс трансформации механических колебаний в нервный процесс с последующим проведением нервного возбуждения в ЦНС, одна из основных функций слухового анализатора (звукопроведение и звуковосприятие).

Существуют различные теории слуха, объясняющие механизм звуковосприятия в спиральном органе - рецепторе слуховой системы.
Известные теории слуха касаются в основном следующих вопросов: в каком участке слуховой системы и как происходит процесс восприятия звуков.
Теории периферического анализа звука
Резонансная теория Гельмгольца
В XIX веке, когда господствующим в медицине было морфологическое направление, в качестве основного критерия, определяющего звуковосприятие, бралась определенная деталь строения слухового органа. Как уже упоминалось, основная мембрана, на которой расположен спиральный орган, при осмотре ее с помощью увеличительной оптики имеет поперечную исчерченность, как бы состоит из «струн» разной длины. Исходя из этого факта, Гельмгольц в 1863 г. создал так называемую резонансную теорию слуха. Согласно этой теории, в улитке возникают явления механического резонанса в отношении звуковых колебаний различных частот. По аналогии со струнными инструментами звуки высокой частоты приводят в колебательное движение участок основной мембраны с короткими волокнами у основания улитки, а звуки низкой частоты — в колебательное движение участок мембраны с длинными волокнами у верхушки улитки (рис. 56). При подаче и восприятии сложных звуков одновременно начинает колебаться несколько участков мембраны. Чувствительные клетки спирального органа воспринимают эти колебания и передают по нерву слуховым центрам.
На основании изучения теории Гельмгольца можно сделать три вывода: 1) улитка является тем звеном слухового анализатора, где возникает первичный анализ звуков; 2) каждому простому звуку присущ определенный участок на основной мембране; 3) низкие звуки приводят в колебательное движение участки основной мембраны, расположенные у верхушки улитки, а высокие — у ее основания.
Таким образом, теория Гельмгольца впервые позволила объяснить основные свойства уха, т. е. определение высоты, силы и тембра. В свое время эта теория нашла много сторонников и до сих пор считается классической. Действительно, вывод Гельмгольца о том, что в улитке происходит первичный пространственный анализ звуков, полностью соответствует теории И. П. Павлова о способности к первичному анализу как концевых приборов афферентных нервов, так и в особенности сложных рецепторных аппаратов. Вывод о пространственном размещении рецепции разных тонов в улитке нашел подтверждение в работах Л. А. Андреева. Согласно его данным, при разрушении верхушки улитки у собак наблюдается выпадение условных рефлексов на низкие звуки, при разрушении ее основного завитка — на высокие звуки.
Резонансная теория Гельмгольца получила подтверждение и в клинике. Гистологическое исследование улиток умерших людей, страдавших островковыми выпадениями слуха, позволило обнаружить изменения кортиева органа в участках, соответствующих утраченной части слуха. Вместе с тем современные знания не подтверждают возможность резонирования отдельных «струн» основной мембраны; следовательно, необходимы более точные объяснения пространственной рецепции звуков в улитке.
Гидродинамические теории
Исследования последнего времени показывают, что под влиянием звуков в лимфе улитки происходят сложные гидродинамические процессы. Это послужило основанием для создания Бекеши и Флетчером гидродинамической гипотезы слуха, которая значительно расширяет резонансную теорию Гельмгольца.

Прямое изучение механических свойств основной мембраны показало, что ей не свойственна высокая механическая избирательность. Звуковые волны различных частот вызывают движения основной мембраны на довольно больших ее участках. Прямые наблюдения с регистрацией колебаний основной мембраны показали, что звуки определенной высоты вызывают на основной мембране «бегущую волну». Гребню этой волны соответствует большее смещение основной мембраны на одном из ее участков, локализация которого зависит от частоты звуковых колебаний. По мере повышения звука прогиб основной мембраны смещается. Наиболее низкие звуки приводят к прогибанию мембраны у верхушки улитки. Основная мембрана смещается на гребне «бегущей волны» и, колеблясь, вызывает деформацию сдвига в волосковых клетках спирального органа над этим участком мембраны.
Позже теорию Гельмгольца дополнил Флетчер. Согласно этой теории, на звуковые волны отвечают не отдельные струны основной перепонки, а пере - и эндолимфа улитки. Пластинка стремечка передает звуковые колебания жидкости улитки к основной перепонке, причем максимум амплитуды этих колебаний при более высоких тонах лежит ближе к основанию улитки, при более низких - ближе к ее вершине. Оканчивающиеся на основной перепонке нервные волокна резонируют лишь на частоты выше 60 - 80 Гц; волокон, воспринимающих более низкие частоты, на основной мембране нет. Тем не менее в сознании формируется ощущение высоты вплоть до 20 Гц. Оно возникает как комбинационный тон высоких гармоний. Таким образом, с точки зрения гипотезы Флетчера, восприятие высоты низких тонов объясняется ощущением всего комплекса гармонических обертонов, а не только восприятием частоты основного тона, как это обычно принималось до сих пор. А так как состав обертонов в значительной степени зависит от силы звуков, то становится понятной тесная связь между тремя субъективными качествами звука - его высотой, громкостью и тембром. Все эти элементы, каждый в отдельности, зависят и от частоты, и от силы, и от состава обертонов звука.
Согласно гипотезе Флетчера, резонансные свойства присущи механической системе улитки в целом, а не только волокнам основной мембраны. Под действием определенного тона колеблются не только резонирующие на данную частоту волокна, но вся мембрана и та или иная масса жидкости улитки. Высокие тоны приводят в движение лишь небольшую массу жидкости вблизи основания улитки, низкие - замыкаются ближе к геликотреме. Флетчер преодолевает также основное затруднение резонансной теории, связанное с объяснением большого диапазона громкости. Он считает, что громкость определяется суммарным числом нервных импульсов, приходящих к мозгу от всех возбужденных нервных волокон основной мембраны.
Теория Флетчера в общем не отрицает существа теории Г. Гельмгольца и может быть отнесена к теориям "периферического анализатора".
Теории Флока и Ухтомского кратко в презентации.
Теории центрального анализа звука
В 1886 г. британский физик Э. Резерфорд выдвинул теорию, которой он пытался объяснить принципы кодирования высоты и интенсивности звука. Его теория содержала два утверждения. Во-первых, по его мнению, звуковая волна заставляет вибрировать всю барабанную перепонку (мембрану), и частота вибраций соответствует частоте звука. Во-вторых, частота вибраций мембраны задает частоту нервных импульсов, передаваемых по слуховому нерву. Так, тон частотой 1000 герц заставляет мембрану вибрировать 1000 раз в секунду, в результате чего волокна слухового нерва разряжаются с частотой 1000 импульсов в секунду, а мозг интерпретирует это как определенную высоту. Поскольку в данной теории предполагалось, что высота зависит от изменений звука во времени, ее назвали временной теорией (в некоторых литературных источниках ее также называют частотной теорией).
Оказалось, что гипотеза Резерфорда не в состоянии объяснить все феномены слуховых ощущений. Например, было обнаружено, что нервные волокна могут передавать не более 1000 импульсов в секунду, и тогда неясно, как человек воспринимает высоту тона с частотой более 1000 герц.
Теория стоячих волн
К этой группе теорий принадлежит теория И. Эвальда, согласно которой при действии звука в улитке образуются стоячие волны с длиной, определяемой частотой звука. Высота тона определяется восприятием формы узора стоячих волн. Ощущению определенного тона соответствует возбуждение одной части нервных волокон; ощущению другого тона - возбуждение другой части. Анализ звуков происходит не в улитке, но в центрах головного мозга. Эвальду удалось построить модель основной мембраны, размером приблизительно соответствующей реальной. При возбуждении ее звуком в колебательное движение приходит вся перепонка; возникает "звуковая картина" в виде стоячих волн с длиной тем меньшей, чем выше звук. Несмотря на удачные объяснения некоторых затруднительных частностей, теория Эвальда (как и другие теории "центрального анализатора") плохо согласуется с новейшими физиологическими исследованиями природы нервных импульсов. С. Н. Ржевкин считает, однако, возможной двойственную точку зрения, а именно объяснение восприятия высоких тонов (не встречающее затруднений) в смысле теории "периферического анализатора", а низких - с точки зрения "центрального анализатора".
Дуалистическая теория Ребула изложена вкратце в презентации к докладу.
Каким образом происходит трансформация механической энергии звуковых колебаний в нервное возбуждение, — на этот вопрос пытались и пытаются дать ответ многие исследователи. Значительный вклад в решение этой задачи сделан отечественными учеными. В основу электрофизиологического метода исследований данной проблемы положено учение Н. Е. Введенского о процессах нервного возбуждения. Согласно его взглядам, ритм возбуждения нервной ткани соответствует ритму раздражения. В результате таких действий появляются электрические колебания, получившие название биотоков, или токов действия. Эти токи, как оказалось, можно регистрировать. Развитие техники позволило не только наблюдать за характером биотоков, но и фиксировать их. При этом оказалось, что улитка способна генерировать определенный переменный электрический потенциал в ответ на определенное звуковое раздражение.
Таким образом, под влиянием деформации волосков рецепторных клеток при давлении покровной (текториальная) мембраны освобождается электрическая энергия синхронно со звуковыми колебаниями — эти потенциалы в виде микрофонных потенциалов отводятся наилучшим образом от самых волосковых клеток, а также от окна улитки благодаря электропроводимости ушной лимфы. Биотоки являются раздражителями тончайших окончаний веточек кохлеарного нерва, оплетающих волосковые клетки. Эти окончания имеют характер синапсов и возбуждение передается при помощи медиаторов (ацетилхолин). Следовательно, спиральный орган работает как детектор, отвечая только на определенный вид энергии (звук), и как трансформатор, превращая звуковую энергию в процесс нервного возбуждения.
Своими опытами по удалению височных долей мозга у собак И. П. Павлов установил, что отдельные элементы слухового анализатора рассеяны по всей коре больших полушарий и в них происходит низший анализ и синтез звуков. Однако высшие процессы анализа и синтеза звуковых раздражений возможны только в центре слухового анализатора, находящегося в коре височных долей.
Студопедия рекомендует:
Расчет изменения энтропии в различных процессах Второй закон термодинамики в виде , записанный для равновесных процессов, позволяет вычислить не абсолютное значение энтропии, а.
Законотворческий процесс в Российской Федерации: понятие и основные стадии Законотворческий процесс - это порядок деятельности органа законодательной власти по созданию законов.
Виды психологической защиты Наиболее распространенные и важные механизмы психологической защиты могут быть представлены в виде нескольких групп.
Гражданская война и интервенция (кратко) Гражданская война началась в октябре 1917 г. и закончилась разгромом белой армии на Дальнем Востоке осенью 1922 г. В течение этого.
Приемы меткого выстрела из пистолета Макарова Приступать к изучению техники стрельбы необходимо только после того.
ЭКГ. Мурашко, Струтынский
В результате нарушения последовательности распространения вс возбуждения при желудочковой экстрасистолии резко измененной оказыва последовательность процесса реполяризации желудочков, что выражается в смещени сегмента RS-Т и выше или ниже изолинии, а также в формировании асимметричног отрицательного или положительного зубца, как при блокадах ножек пучка (подробнее см. ниже). При правожелудочковой экстрасистолии наблюдаются депрессия сегмент RS-Т' и отрицательный асимметричный зубец Т экстрасистоли желудочкового комплекса в левых грудных отведениях(V5, V6), три левожелудочковой экстрасистолии — в правых грудных отведениях (V1, V2). Как видно на рисунке 5.12, смещение сегмента RS—T и зубец Т при желудочковой экстрасистолии дискордантн основному зубцу желудочкового экстрасистолического комплекса QRS, т.е. направлены в сторону, противоположную этому зубцу. Если в том или электрокардиографическом отведении желудочковая экстрасистола представле основном широким деформированным зубцом R', сегмент RS-T смещен ниже изолинии и имеется отрицательный асимметричный зубец Т с пологим нисходящим и кр восходящим коленом (рис. 5.12). Наоборот, если основным зубцом комплексаQRS является деформированный расширенный зубецS', сегмент RS—Т' расположен выше изолинии и на ЭКГ регистрируется положительный асимметричный зубец Т.
является отсутствие перед экстрасистолическим комплексомQRS' зубца
наличие полной компенсаторной паузы.
Лишь иногда, обычно на фоне относительно редкого основного синусового ритма, компенсаторная пауза после желудочковой экстрасистолы может отсутствовать. Это объясняется тем, что очередной (первый после экстрасистолы) синусовый импуль достигает желудочков в тот момент, когда они уже вышли из состояния рефрактерности. Как видно на рисунке 5.13, в этих случаях экстрасистола как бы вставлена между двумя нормальными желудочковыми комплексами без какой бы то ни было компенсатор паузы. Это так называемые вставочные, или интерполированные, желудочковые экстрасистолы. Компенсаторная пауза может отсутствовать и при желудо экстрасистолии на фоне мерцательной аритмии.
1)преждевременное внеочередное появление на ЭКГ измененного желудочковог
расширение и деформация
сегмента RS-Т и зубца Т
направлению основного зубца комплекса QRS;
4) отсутствие перед желудочковой экстрасистолой зубца Р;
5) наличие в большинстве случаев после желудочковой экстрасистолы полно компенсаторной паузы.
Желудочковая экстрасистолия органического происхождения в целом имеет бол серьезный прогноз, чем суправентрикулярные экстрасистолы, существенно повыша риск внезапной смерти. Речь идет о так называемых угрожающих желудочк экстрасистолах, к которым относятся: 1) частые желудочковые экстрасистолы; 2) политопные (полифокусные) желудочковые экстрасистолы; 3) парные (групповые) желудочковые экстрасистолы; 4) ранние желудочковые экстрасистолы.
Такие «угрожающие» экстрасистолы нередко являются предвестниками б тяжелых нарушений ритма— пароксизмальной желудочковой тахикардии фибрилляции или трепетания желудочков (см. разделы 5.3.2 и 5.3.5).
5.3.2. Пароксизмальная тахикардия
Пароксизмальная тахикардия — это внезапно начинающийся и так же внеза заканчивающийся приступ учащения сердечных сокращений до140—250 в минуту при сохранении в большинстве случаев правильного регулярного ритма. Он обусловле частыми эктопическими импульсами, исходящими из предсердий, АВ-соединения или из желудочков.
Приступ пароксизмальной тахикардии продолжается обычно от нескольких секун до нескольких часов, лишь изредка дольше. Больные в большинстве случаев ощущаю внезапное начало и окончание приступа.
Важным признаком любой пароксизмальной тахикардии является сохранени течение всего пароксизма(кроме первых нескольких циклов) правильного ритма постоянной частоты сердечных сокращений, которая в отличие от сину тахикардии не изменяется после физической нагрузки, эмоционального напряжения, при
глубоком дыхании или после инъекции атропина.
тахикардии: 1) механизм повторного входа волны возбуждения(re-entry); 2) повышение автоматизма клеток проводящей системы сердца - эктопических центров II и III порядка (более редкий механизм).
Эти механизмы не случайно сходны с механизмами возникновения экстрасистолии, поскольку при определенных допущениях и сам приступ пароксизмальной тахикард
можно рассматривать как длинный ряд следующих одна за другой с большой частотой экстрасистол, источником которых является путь повторного входа эктопический центр, расположенный в предсердиях, АВ-узле или желудочках.
В последние годы все большее значение в генезе пароксизмальной тахика придается именно механизмуre-entry, ведущему к многократно повторяющем круговому движению волны возбужденияo определенному участку проводящ системы сердца, что и является источником частых эктопических импульсов. Для осуществления механизма re-entry необходим ряд условий, в первую очер существование двух независимых друг от друга в функциональном или анатомическо
формировании электрической негомогенности различных участков сердечной мышцы ее проводящей системы у больных с острым инфарктом миокарда, хронической ишемической болезнью сердца, миокардитами и некоторыми другими заболеваниями, а
также у лиц с врожденными аномалиями развития
например у больных с дополнительными аномальными путями быстрого проведения—
синдромом WPW, CLC и т.д. ( см.
главу 6 ) или с так
функциональной диссоциацией АВ-узла
В зависимости от локализации
или постоянно циркулирующей возвратной волны возбуждения(re-entry) различают
5.3.2.1. Предсердная пароксизмальная тахикардия
При предсердной пароксизмальной тахикардии источник частой патологичес импульсации расположен в предсердиях. Основным электрокардиографически признаком этой формы пароксизмальной тахикардии является наличие зубца' передР каждым желудочковым комплексом QRS (рис. 5.14). В связи с тем, что распространение волны возбуждения по предсердиям изменено, зубец Р', как правило, деформирован (например, в отведениях II, III, aVF он может быть отрицательным при расположени эктопического очага в нижних отделах предсердий) (рис. 5.14, а).
Поскольку при предсердной пароксизмальной тахикардии волна возбуж
распространяется по желудочкам обычным путем
пароксизмальной тахикардии. В
редких случаях, так
экстрасистолии, могут наблюдаться уширенные и деформированные аберра желудочковые комплексы QRS, обусловленные преходящей блокадой одной из нож пучка Гиса.
Интервал P—Q(R) часто бывает удлиненным более 0,2 с, что отражает замедление проводимости по АВ-узлу— атриовентрикулярную блокаду I степени. Нередко при очень частой патологической предсердной импульсации АВ-узел не может провести все импульсы к желудочкам. В связи с этим к желудочкам проводится, например, каждый второй или каждый третий импульсразвивается атриовентрикулярная блокадаII степени с периодическим выпадением отдельных желудочковых комплексов(подробнее см. главу 6 ).
В некоторых случаях, особенно у пожилых людей с ишемической болезнью сердца,
наблюдаться смещение сегмента RS—Т ниже изолинии и формирование отрицательного зубца Т. Это является отражением коронарной недостаточности и ишемии сердечн мышцы, которая возникает на фоне учащенного ритма, поскольку увеличение ЧС ведет у этих больных к увеличению потребности миокарда в кислороде, которая не удовлетворяется при коронаросклеро. В некоторых случаях развивается с коронарных артерий.
Наиболее характерными электрокардиографическими признаками предсердно пароксизмальной тахикардии являются:
1) внезапно начинающийся и так же внезапно заканчивающийся пр учащения сердечных сокращений до 140—250 в минуту при сохранении правильного ритма;
2) наличие перед каждым желудочковым комплексомQRS' сниженного, деформированного, двухфазного или отрицательного зубца Р;
3) нормальные неизмененные желудочковые комплексыQRS, похожие на QRS, регистрировавшиеся до возникновения приступа пароксизмальной тахикарди(за исключением редких случаев с аберрацией желудочкового проведения);
4) в некоторых случаях наблюдается ухудшение атриовентрику проводимости с развитием атриовентрикулярной блокадыI степени (удлинение интервала P—Q(R) более 0,2 с) или II степени с периодическими выпадениям отдельных комплексов QRS' (непостоянные признаки).
5.3.2.2. Пароксизмальная тахикардия из атриовентрикулярного соединения
расположен в области АВ-соединения. Электрокардиографические
пароксизмальной тахикардии очень схожи
тахикардии. На ЭКГ фиксируется внезапное учащение сердечных сокращений до140— 220 в минуту при сохранении в большинстве случаев правильного ритма. Частота сердечных сокращений в момент пароксизма практически не изменяется под влияни физической и психической нагрузки, при дыхании или после введения атропина.
Так же как при предсердной форме пароксизмальной , при
атриовентрикулярной пароксизмальной тахикардии желудочковые комплексыQRS не изменены, поскольку волна возбуждения распространяется по желудочкам обычны путем - по пучку Гиса и волокнам Пуркинье. Довольно редко наблюдаются аберрантные желудочковые комплексы QRS — уширенные и деформированные.
Главным и, пожалуй, единственным отличием этой формы пароксизмал тахикардии от предсердной является иное соотношение во времени желудоч комплексов QRS и предсердных зубцов Р. Поскольку эктопический импульс п пароксизмальной тахикардии из АВ-соединения распространяется по предсердиям обычным путем, а ретроградно — снизу вверх, зубцы Р в отведениях II, III и aVF при этой форме тахикардии всегда отрицательные. Если эктопический импульс достигае желудочков раньше, чем предсердий, отрицательный зубец Р регистрируется поза комплекса QRS, обычно между зубцами R и T (рис. 5.14, б). Если эктопический импульс одновременно достигает предсердий и желудочков, то комплекс QRS' и зубец P' сливаются друг с другом. В таких случаях зубцы Р вообще невозможно обнаружить н ЭКГ (рис. 5.14, в).
Наиболее характерными электрокардиографическими пароксизмальной тахикардии из АВ-соединения являются:
1) внезапно начинающийся и так же внезапно заканчивающийся пр учащения сердечных сокращений до140-220 в минуту при сохранении правильног ритма;
2) наличие в отведениях II, III и aVF отрицательных зубцов Р', расположенных позади комплексов QRS' или сливающихся с ними и не регистрирующихся на ЭКГ;
3) нормальные неизмененные (неуширенные и недеформированные) желудочковые комплексы QRS', похожие на QRS, регистрировавшиеся д
относительно редких случаев с аберрацией желудочкового проведения).
и атриовентрикулярную формы пароксизмальной тахикардии
понятием «наджелудочковая (суправентрикулярная) пароксизмальная
наиболее типичными электрокардиографическими признаками которой являются:
1) увеличение ЧСС до 140-220 в минуту;
2) нормальные неизмененные желудочковые комплексыQRS, похожие н комплексы QRS, регистрировавшиеся до приступа пароксизмальной тахикардии;
3) отсутствие зубца Р на ЭКГ или наличие его перед либо после каждого комплекса
5.3.2.3. Желудочковая пароксизмальная тахикардия
При желудочковой пароксизмальной тахикардии источник эктопических импульсов расположен в проводящей системе желудочков— пучке Гиса, ветвях пучка Гиса или
инфаркте миокарда или
Так же как при суправентрикулярной пароксизмальной тахикардии, наблюдается внезапное начало приступа желудочковой тахикардии с увеличением ЧСС до 140—220 в минуту. В большинстве случаев ритм остается правильным. Однако в отличие предсердной или атриовентрикулярной тахикардии при желудочковой пароксизмально тахикардии ход возбуждения по желудочкам резко нарушен: эктопический импульс, возникший в каком-либо разветвлении пучка Гиса, вначале возбуждает один желудочек, а затем с большим опозданием переходит на второй желудочек и распространяется нему необычным путем. В результате изменения хода волны возбужден желудочкам вторично резко нарушенным оказывается и процесс их реполяризации. Все эти изменения очень напоминают таковые при желудочковой экстрасистолии, а также при блокадах ножек пучка Гиса(см. ниже). Поэтому сходными оказываются изменения желудочкового комплекса QRS' сегмента RS— Т и зубца Т. При желудочково пароксизмальной тахикардии комплексQRS деформирован и уширен, его продолжительность превышает 0,12 с (рис. 5.15). Сегмент RS—T и зубец T, так же как при желудочковой экстрасистолии, располагаются дискордантно по отношению основному зубцу комплекса QRS. В тех отведениях, где основным зубцом комплекс является зубец R, сегмент RS—Т смещен ниже изоэлектрической линии, а зубец Т отрицательный. Если основной зубец комплекса QRS направлен вниз (зубец S или комплекс QS), сегмент RS—Т располагается выше изолинии, а зубец Т положительный
Важным электрокардиографическим признаком желудочковой пароксизмаль тахикардии является так называемая атриовентрикулярная(предсердно-желудочковая) диссоциация (АВ-диссоциация), т.е. полная разобщенность в деятельности предсердий и желудочков. Дело в том, что эктопические импульсы, возникающие в желудочках, не проводятся ретроградно через АВ-узел к предсердиям. Предсердия возбуждаютс обычным путем за счет импульсов, исходящих из СА-узла. В большинстве случае синусовый импульс достигает АВ-узла в тот момент, когда тот находится в состояни рефрактерности. Это происходит потому, что частота импульсов, исходящих и желудочков, примерно в 2—3 раза превышает частоту синусового ритма. АВ-узел, испытывая такую «бомбардировку» электрическими импульсами, большую част времени находится в рефрактерной фазе. По этой причине синусовые импульсы чащ всего не проводятся на желудочки. Таким образом, желудочки возбуждаются сокращаются в своем— очень частом — ритме, источником которого являет эктопический очаг, рас положенный в желудочках, а предсердия возбуждаются за сче нормальных синусовых импульсов. На ЭКГ при этом могут регистрироваться обычные, неизмененные положительные зубцы , следующие друг за другом через ра
интервалы времени с частотой около 70-90 в минуту. Важно отметить, что зубцы Р
наслаиваются на различные участки комплексаQRST, то регистрируясь
комплексом QRS или после него, то сливаясь с зубцами R, S или Т, как это показано на
Теория эктопических центров. Теория круговой волны
Возмущение в какой-либо точке поверхности жидкости вызывает появление кольцевых волн с центром в точке возмущения.
Для изучения этих волн введем цилиндрические координаты с началом в месте возмущения и осью направленной вертикально вниз. Уравнение Лапласа (2) для потенциала скоростей в силу формулы (3) гл. XIX, примет при этом вид
Рассмотрим сначала колебания чисто периодические по времени, в связи с чем, согласно § 1, примем
где — круговая частота колебаний, комплексная функция координат, как и удовлетворяющая уравнению вида (38). Считая, что интересующие нас волны имеют кольцевую симметрию, придем к уравнению
Полагая далее бассейн неограниченным, сохраним граничные условия только для свободной поверхности (13):
и для дна бассейна (12):
Как и в предыдущем параграфе, решение уравнения (40) будем искать по методу разделения переменных. Положив и после очевидных выкладок придем к уравнениям:
где — произвольное число.
Оба граничных условия относятся к уравнению (44). Как само уравнение (44), так и эти граничные условия те же, что и в § 2. Поэтому на основании формулы (21) сразу можем записать, что с точностью до множителя,
причем, в силу (22), вещественное число, связанное с круговой частотой колебаний (о уравнением
Что же до уравнения (43), то это уравнение Бесселя нулевого порядка (гл. XIII). Его решением, ограниченным и непрерывным при всех включая является функция Бесселя нулевого порядка Таким образом, принимая во внимание соотношения (39) и (45), придем к заключению, что все непрерывные решения уравнения (40) при граничных условиях (41) — (42) имеют вид
где — величина, не зависящая ни от ни от Отсюда, на основании равенства (39),
В силу формулы (7), высота свободной поверхности над ее невозмущенным уровнем определится соотношением
Воспользовавшись графиком функции легко видеть, что расстояние между двумя соседними вершинами рассматриваемых
периодических кольцевых волн (аналог длины волны в двумерном случае) увеличивается по мере удаления от точки а высота волн убывает.
Рассмотрим теперь случай произвольного осесимметричного начального возмущения.
Предположим, что при
где заданная непрерывная функция и поставим задачей найти движение жидкости при Воспользуемся с этой целью интегралом Фурье — Бесселя:
заменив в нем функцию функцией Введя функцию
Это соотношение дает представление начального возмущения в форме суперпозиции кольцевых волн разных частот. Отсюда ясно, что функция
дает решение нашей задачи. Действительно, эта функция представляет суперпозицию функций (47), удовлетворяющих уравнению задачи и граничным условиям. Следовательно, она также обладает этими свойствами. В силу же (7) из нее вытекает, что
откуда при получаем соотношение (51). Таким образом, функция представляет потенциал скорости жидкости при заданных граничных и начальном условиях и поэтому определяет искомое движение жидкости. Формула (53) определяет форму поверхности жидкости при
Как уже отмечалось, кинематическая теория, правильно описывая основной механизм трехмерной голограммы, не дает количественных соотношений; в частности, с ее помощью нельзя рассчитать дифракционную эффективность. Вместе с тем знание закономерностей, которые определяют эту весьма важную величину,
и параметров, от которых она зависит, играют определяющую роль при разработке технологии изготовления фотоматериалов, предназначенных для записи тех или иных типов трехмерных голограмм. При этом для оценки качества фотоматериала, как правило, используют некоторую условную величину — дифракционную эффективность простейшей объемной решетки, полученной в результате регистрации картины интерференции двух плоских волн.
Рис. 5. К рассмотрению теории связанных волн. V — объем голограммы; лучевые векторы плоских волн, экспонировавших голограмму при записи; слои диэлектрика, образовавшиеся на месте поверхностей пучностей стоячей волны. Голограмма при освещении ее волной восстанавливает волну с лучевым вектором параллельным в свою очередь волна восстанавливает волну волна волну и т. д. Интенсивность восстановленной голограммой волны определяется посредством суммирования всех составляющих с учетом их фаз. Справа приведен график зависимости дифракционной эффективности от толщины голограммы.
Именно в применении к решению этой весьма важной задачи и используется в основном теория связанных волн, предложенная американским, исследователем Когельником [7]. Рассмотрим соответствующий этой теории механизм взаимодействия света с решеткой несколько подробнее.
Предположим, что на голограмме записаны две плоские волны о лучевыми векторами и что после проявления в ее объеме Образовалась гармоническая фазовая решетка — система плоских слоев отличающихся значением показателя преломления (рис. 5). Пусть при восстановлении на такую структуру падает одна из образовавших ее плоских волн, например 10. В соответствии с представлениями кинематической теории восстанавливающая волна проходя без затухания через объем
голограммы, преобразуется во всех точках этого объема в волну которая выходит из голограммы, не взаимодействуя с ее структурой.
Теория связанных волн внесла в эти представления уточнения. Очевидно, что восстановленная волна прежде чем покинуть объем голограммы, испытает взаимодействие с ее структурой и в результате частично преобразуется в волну совпадающую по направлению с волной 10 — второй из волн, записанных на голограмме. Волна в свою очередь снова трансформируется в волну совпадающую по направлению с волной
Таким образом, на первоначальные падающую и восстановленные волны накладываются вторичные волны, совпадающие с ними по направлению, но отличающиеся по фазе. Результат сложения этих волн не является тривиальным. Например, в рассматриваемом случае при некоторой толщине голограммы вся энергия перекачивается в волну т. е. дифракционная эффективность становится равной 100%. При дальнейшем увеличении толщины голограммы до значения вся энергия переходит в волну и дифракционная эффективность голограммы становится равной нулю и т. д.
Последовательность преобразований теории связанных волн сначала формально совпадает с соответствующей последовательностью теории первого приближения [см. выражения (13) — (15)]. Отличие состоит лишь в том, что в выражении (14) волны считают равноправными и в выражении (15) поэтому нельзя пренебречь третьим членом. Учет связи падающей и восстановленной голограммой волн основан на рассмотренном ранее свойстве структуры голограммы преобразовывать в каждой своей точке одну из интерферирующих компонент в другую [см. выражение В частном случае, когда на голограмме записана пара плоских волн, амплитуда которых не зависит от пространственных координат, указанное свойство действительно как при преобразовании так и наоборот. Учитывая это, а также опуская члены, соответствующие преобразованиям типа выражение (15) можно записать следующим образом:
Поскольку это уравнение выполняется при произвольном выборе пары плоских волн и записываемых на голограмме, то суммы членов, одна из которых содержит только а другая — должны обращаться в нуль по отдельности. Следовательно, мы получаем систему двух уравнений:
Нетрудно заметить, что эти уравнения связаны друг с другом: в уравнение для волновой функции входит амплитуда волновой функции и наоборот. Подставляя в (28) и (29) вместо и
выражения для плоских волн, аналогичные (19) и (20), получаем два уравнения для амплитуд с помощью которых можно найти зависимость этих амплитуд от толщины голограммы.
Используя такой подход, Когельник рассмотрел наиболее характерные случаи записи. В частности, он показал, что дифракционная эффективность фазовой отражательной решетки при некоторой достаточно большой толщине стремится к 100%. Дифракционная эффективность такой же амплитудной решетки не превышает 7,2%.
Однако следует заметить, что теорию связанных волн нельзя рассматривать как теорию трехмерной голограммы во втором приближении. Действительно, голограмма по своему физическому смыслу представляет собой запись информации о сложном волновом поле, которое можно представить в виде суммы множества плоских волн. Поэтому решетку, образованную в результате записи картины интерференции двух плоских волн, свойства которой рассматриваются в теории Когельника, можно назвать голограммой только условно.
Теорию Когельника нельзя считать теорией даже элементарного механизма голограммы — процесса записи и восстановления двух плоских волн, на основе которого можно было бы разработать общую теорию, учитывающую закономерности записи и воспроизведения произвольного волнового фронта, составленного из множества плоских волн. Трудность здесь обусловлена тем, что одна и та же плоская волна, как правило, участвует в создании множества решеток. В таких условиях практически все решетки оказываются связанными друг с другом, и поле излучения, восстановленное голограммой, в отличие от первого приближения уже нельзя представить в виде простой суммы полей, соответствующих отдельным решеткам. При этом теория Когельника не дает ответа на основной вопрос о том, как учесть все эти связи.
Более плодотворным путем развития теории трехмерной голограммы оказался подход, предложенный Эвальдом [8] и основанный на идеях динамической теории дифракции рентгеновских лучей. Первоначально эта теория применялась для изучения простой объемной голографической решетки [9]. Впервые для анализа собственно объемной голограммы, т. е. структуры, составленной из множества решеток, ее использовали Аристов и Шехтман (см., например, [10]) В этих работах, в частности, было показано, что, в случае когда голограмма получена с участием мощной опорной ролны, а также когда записанная на голограммах волна имеет сложную структуру, для определения интенсивности восстановленной волны можно пользоваться формулами Когельника.
Представления, основанные на динамической теории дифракции, нашли наибольшее выражение в так называемой модовой теории трехмерной голограммы, предложенной Сидоровичем [11].
По существу эта теория обобщает введенное Эвальдом понятие волны, согласованной с периодической неоднородной структурой. В теории Эвальда это понятие удалось применить только к простейшей объемной решетке — пространственной гармонике показателя преломления. Например, в случае, представленном на рис. 6, согласованными волнами фазовой решетки являются две пары плоских волн — пара, характеризующаяся волновыми векторами и пара Пара и 1д образует стоячую волну, максимумы распределения интенсивности которой совпадают с максимумами функции распределения показателя преломления решетки. Распределение интенсивности такой стоячей волны приведено в нижней части рисунка в виде сплошной кривой. Пара образует стоячую волну, максимумы которой совпадают с минимумами показателя преломления решетки. На рис. 6 соответствующая кривая отмечена штриховой линией. Таким образом, первая согласованная волна распространяется как бы через однородную среду с показателем преломления ямакс. а вторая — через среду с показателем преломления пмин. При этом решетка действует так, как если бы различные согласованные волны, проходя через среды с различными значениями показателя преломления, изменяли бы свою относительную разность фаз.
Рис. 6. К рассмотрению модовой теории трехмерной голограммы. Понятие волны, согласованной с периодической структурой, слои гармоники характеризующиеся максимальным значением показателя преломления; пара волн, создающая стоячую волну, максимумы которой совпадают со слоями — пара волн, создающая стоячую волну, максимумы которой располагаются между слоями Внизу приведен график распределения интенсивности стоячей волны
Обсуждаемая модовая теория трехмерной голограммы доказывает то, что согласованные волны (моды) можно сопоставлять не только простейшим периодическим структурам, но также и трехмерным голограммам — объемным структурам, полученным в результате регистрации интенсивности сложных волновых полей. Оказывается, что каждой трехмерной голограмме соответствует полная система согласованных с нею волн (мод) и что любую волну, эффективно взаимодействующую с трехмерной голограммой, можно
разложить по этим модам. В частности, применительно к фазовой голограмме теория предполагает, что каждая мода проходит через голограмму как через однородную среду с определенным показателем преломления. В этом случае действие голограммы состоит в том, что она сдвигает относительную разность фаз между модами.
В общих чертах рассмотрение проводится следующим образом. Волну, записанную на голограмме, представляют в виде суммы плоских волн:
Подставив это значение в выражение (6), найдем с помощью соотношения (12) функцию распределения диэлектрической проницаемости голограммы:
Будем считать, что условиям распространения света через данную среду удовлетворяют специальные волновые функции (моды)
Относительно этих функций предполагается, что они составлены из тех же плоских волн, которые участвовали в записи голограммы, однако их направления распространения вследствие изменения диэлектрической проницаемости среды после экспозиции стали несколько другими. Кроме того, будем считать, что для любых компонент данной моды это изменение диэлектрической проницаемости одинаково. Все эти условия имеют вид специальных соотношений между волновыми векторами моды к и волновыми векторами излучения, записанного на голограмме.
Подставляя в уравнение Гельмгольца (13) выражение (32) для и учитывая упомянутые соотношения между можно получить систему уравнений, связывающих амплитуды компонент моды с амплитудами составляющих поля, записанного на голограмме. В матричной форме эти уравнения имеют вид
где матрица голограммы, составленная из коэффициентов, линейная матрица амплитуд 1-й моды, бег — значение диэлектрической проницаемости, соответствующее 1-й моде. Таким образом, задача сводится к нахождению собственных функций и собственных значений оператора характеризующего структуру голограммы. Поскольку этот оператор является самосопряженным, система его собственных функций (мод)
составляет полный ортогональный базис, по которому можно разложить любую волновую функцию, составленную из плоских волн, экспонировавших голограмму.
Модовая теория существенно упрощает рассмотрение процессов, протекающих в трехмерной голограмме, благодаря тому, что она автоматически учитывает очень сложные взаимные связи между рассеянием света на множестве решеток, из которых составлена голограмма, а также и потому, что аналогично теориям первого приближения представляет результат в виде суперпозиции независимых функций. Конкретно модовая теория была развита в применении к фазовым пропускающим [11, 12], амплитудным усиливающим [13] и трехмерным отражательным голограммам [14]. В настоящее время наиболее актуальным является применение модовой теории к описанию отражения света «бриллюэновским зеркалом» [15]. В данном случае модовая теория правильно предсказывает значение полного коэффициента усиления в среде, которое необходимо, чтобы амплитуда обращенной волны превышала шумы. Модовая теория позволяет также сформулировать условия устойчивости обращенной волны при ее распространении сквозь усиливающую голограмму. Все это нашло подтверждение в большом числе экспериментов.
Читайте также:
