Геометрический метод решения задачи линейного программирования шпора

Назначение сервиса . С помощью данного сервиса можно в онлайн режиме решить задачу линейного программирования геометрическим методом, а также получить решение двойственной задачи (оценить оптимальность использования ресурсов). Дополнительно создается шаблон решения в Excel .

• Решение онлайн
• Видеоинструкция
• Оформление Word
• Также решают

Решение задачи линейного программирования графическим методом включает следующие этапы:

1. На плоскости X₁0X₂ строят прямые.
2. Определяются полуплоскости.
3. Определяют многоугольник решений;
4. Строят вектор N(c₁,c₂), который указывает направление целевой функции;
5. Передвигают прямую целевую функцию c₁x₂ + c₂x₂ = 0 в направлении вектора N до крайней точки многоугольника решений.
6. Вычисляют координаты точки и значение целевой функции в этой точке.

Пример . Компания изготавливает два вида продукции – П1 и П2. Для производства продукции используются два вида сырья – С1 и С2. Оптовые цены единицы продукции равна: 5 д.е. для П1 и 4 д.е. для П2. Расход сырья на единицу продукции вида П1 и вида П2 дан в таблице.
Таблица - Расход сырья на производство продукции

Сырье	Расход сырья на 1 ед. продукции		Максимальный запас сырья, ед.
	П1	П2
М1	6	4	24
М2	1	2	6

Установлены ограничения на спрос продукции: ежедневный объем производства продукции П2 не должен превышать ежедневный объем производства продукции П1 не более чем на 1 тонну; максимальный ежедневный объем производства П2 не должен превышать 2 т.
Требуется определить:
Какое количество продукции каждого вида должно производить предприятие, чтобы доход от реализации продукции был максимальным?

1. Сформулировать математическую модель задачи линейного программирования.
2. Решить задачу линейного программирования графическим способом (для двух переменных).

Решение.
Сформулируем математическую модель задачи линейного программирования.
x₁ – производство продукции П1, ед.
x₂ – производство продукции П2, ед.
x₁, x₂ ≥ 0

Если количество переменных в задаче линейного программирования больше двух, то задачу предварительно сводят к стандартной ЗЛП.
F(X) = 3x₁ - 2x₂ + 5x₃ - 4x₅ → max при ограничениях:
x₁ + x₂ + x₃=12
2x₁ - x₂ + x₄=8
- 2x₁ + 2x₂ + x₅=10
F(X) = 3x₁ - 2x₂ + 5x₃ - 4x₅
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:

1	1	1	0	0	12
2	-1	0	1	0	8
-2	2	0	0	1	10

Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x₃.
2. В качестве базовой переменной можно выбрать x₄.
3. В качестве базовой переменной можно выбрать x₅.
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Соответствующие уравнения имеют вид:
x₁ + x₂ + x₃ = 12
2x₁ - x₂ + x₄ = 8
- 2x₁ + 2x₂ + x₅ = 10
Выразим базисные переменные через остальные:
x₃ = - x₁ - x₂+12
x₄ = - 2x₁ + x₂+8
x₅ = 2x₁ - 2x₂+10
Подставим их в целевую функцию:
F(X) = 3x₁ - 2x₂ + 5(- x₁ - x₂+12) - 4(2x₁ - 2x₂+10)
или
F(X) = - 10x₁ + x₂+20 → max
Система неравенств:
- x₁ - x₂+12 ≥ 0
- 2x₁ + x₂+8 ≥ 0
2x₁ - 2x₂+10 ≥ 0
Приводим систему неравенств к следующему виду:
x₁ + x₂ ≤ 12
2x₁ - x₂ ≤ 8
- 2x₁ + 2x₂ ≤ 10
F(X) = - 10x₁ + x₂+20 → max

Особенности решения задач линейного программирования графическим методом

Далее задача решается графическом способом.

Однако данный метод является наглядным, поэтому рассмотрим его подробно.

Итак, для рассматриваемого случая математическая модель задачи имеет вид:

Мы уже знаем, что множество допустимых решений системы ограничений является выпуклым с конечным числом угловых точек. Задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой целевая функция принимает максимальное значение.

Рассмотрим пример геометрического решения задачи линейного программирования, используя задачу об оптимальном использовании ресурсов.

Для производства двух видов изделий А и В предприятие использует три вида сырья. Нормы расхода сырья каждого вида на изготовление единицы продукции данного вида приведены в таблице. Здесь же указаны прибыль от реализации одного изделия каждого вида и общее количество сырья данного вида, которое может быть использовано предприятием.

Вид сырья	Нормы расхода сырья (кг) на одно изделие	Общее количество сырья (кг)
А	В
I
II
III
Прибыль от реализации одного изделия (ден. ед.)

Требуется составить такой план выпуска изделий, при котором прибыль предприятия от реализации всех изделий является максимальной.

Общая прибыль от реализации изделий, т.е. целевая функция имеет вид:

Найдем решение задачи, используя ее геометрическую интерпретацию.

Определим многоугольник решений.

Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенства заменим на знаки точных равенств и построим соответствующие прямые (рис. 5.6):

Следовательно, если предприятие изготавливает 12 изделий вида А и 18 изделий вида В, то оно получит максимальную прибыль, равную:

Приведем основные этапы геометрического метода решения задачи линейного программирования:

- строят прямые, уравнения которых получают заменой знаков неравенств на знаки точных равенств;

- находят полуплоскости, определяемые каждым из ограничений задачи;

- находят многоугольник решений;

- строят линию уровня F=c₁x₁+c₂x₂=h, проходящую через многоугольник решений;

- определяют координаты точки максимума функции F и вычисляют значение целевой функции в этой точке.

При этом возможны следующие случаи:

- оптимальное решение единственно. Прямая F_max имеет единственную общую точку (В) с многоугольником допустимых решений (рис. 6);

- максимальное значение целевая функция принимает в точке А, а минимальное – в точке В, т.е. прямая F дважды становится опорной по отношению к многоугольнику решений (рис. 7);

- оптимальных решений бесконечное множество. Прямая F_max совпадает с одной из сторон, ограничивающих многоугольник (рис. 8). В этом случае каждая точка отрезка АВ является оптимальным решением;

- оптимального решения не существует по причине неограниченности функции цели (9);

- оптимального решения не существует по причине противоречивости системы ограничений (система неравенств несовместна и область допустимых решений пустое множество, рис. 10).

Окончательно анализируя оптимальные решения основной задачи линейного программирования на плоскости, можно отметить их следующие свойства:

- оптимальное решение, если оно существует, лежит не внутри, а на границе области допустимых решений;

- если решение единственное, оно достигается в одной из вершин области допустимых решений;

- если решений множество, они достигаются на одной из сторон выпуклого многоугольника;

- решение, лежащее в одной из вершин области допустимых решений, является опорным решением (или базисным), а сама вершина – опорной точкой;

- для того чтобы найти оптимальное решение, в принципе достаточно перебрать все вершины (опорные точки) области допустимых решений и выбрать из них ту, в которой функция F достигает максимума.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

Пример 6.1. Решить следующую задачу ли-нейного программирования геометрическим методом:

Решение:

Задача линейного программирования задана в стандартной форме и имеет два проектных параметра, следовательно

, воз-можно ее решение геометрическим методом.

1 этап: построение прямых, ограничивающих область допустимых решений ( ОДР).

Рассмотрим систему ограничений задачи линейного програм-мирования (для удобства пронумеруем неравенства):

Рассмотрим первое ограничение, заменим знак неравенства знаком равенства и выразим переменную х2 через х1:

Для построения прямой по данному уравнению зададим две произвольные точки, к примеру:

Аналогично определяем точки для остальных ограничений системы и строим по ним прямые, соответствующие каждому неравенству (рис. 1). Прямые пронумеруем согласно принятой ранее схеме.

2 этап: определение решения каждого из нера-венств системы ограничений.

Определим полуплоскости – решения каждого из неравенств.

Рассмотрим первое неравенство системы ограничений задачи. Возьмем какую-либо точку (контрольную точку), не принадлежащую соответствующей данному неравенству прямой, например, точку (0; 0). Подставим ее в рассматриваемое неравенство:

При подстановке координат контрольной точки неравенство остается справедливым. Следовательно, множество точек, принадлежащих данной прямой (т.к. неравенство не строгое), а также расположенных ниже ее, будут являться решениями рассматриваемого неравенства (пометим на графике (рис. 1) найденную полуплоскость двумя стрелками направленными вниз рядом с прямой I) .

Аналогично определяем решения других неравенств и соответственно помечаем их графике. В результате график примет следующий вид:

3 этап: определение ОДР задачи линейного про- граммирования.

Найденные полуплоскости (решения каждого из неравенств системы ограничений) при пересечении образуют многоугольник ABCDEO, который и является ОДР рассматриваемой задачи.

Рис. 1. Область допустимых решений задачи

4 этап: построение вектора-градиента.
Вектор-градиент показывает направление максимизации целевой функции . Определим его координаты: координаты начальной его точки (точки приложения) – (0; 0), координаты второй точки:

Построим данный вектор на графике (рис. 2).

5 этап: построение прямой целевой функ-ции.

Рассмотрим целевую функцию данной задачи:

Для построения прямой по данному уравнению зададим две произвольные точки, к примеру:

Построим прямую соответствующую целевой функции (рис. 2).

Рис. 2. Построение целевой функции F(X) и вектора-градиента С

6 этап: определение максимума целевой функ-ции.

Перемещая прямую F(X) параллельно са-мой себе по направлению вектора-градиента, определяем крайнюю точку (точки) ОДР. Согласно графику (рис. 3), такой точкой является точка С ­– точка пересечения прямых I и II.

Рис. 3. Определение точки максимума целевой функции F(X)

Определим координаты точки С, с этой целью, решим сле-дующую систему линейных уравнений:

Подставим найденные координаты в целевую функцию и найдем ее оптимальное (максимальное) значение:

Ответ: при заданных ограничениях макси-мальное значение целевой функции F(Х)=24, которое достигается в точке С, координаты которой х1=6, х2=4.

Пример 6.2. Решить задачу линейного про- граммирования геометрическим методом:

Решение:

Этапы 1-3 аналогичны соответствующим этапам предыдущей задачи.
4 этап: построение вектора-градиента.
Построение вектора-градиента осуществляется аналогично, как и в предыдущей задаче. Построим данный вектор на графике (рис. 4). Отметим также на данном графике стрелкой направление, обратное вектору-градиенту, – направление минимизации целевой функцииF (X).

5 этап: построение прямой целевой функ-ции.

Построение прямой целевой функции F(X) осуществляется аналогично, как и в предыдущей задаче (результат построения приведен на рис. 4).

Рис. 4. Построение целевой функции F(x) и вектора-градиента С

6 этап: определение оптимума целевой функ-ции.

Перемещая прямую F(x) параллельно са-мой себе в направлении, обратном вектору-градиенту, опреде-ляем крайнюю точку (точки) ОДР. Согласно графику (рис. 5), та- кой точкой является точка О с координатами (0; 0).

Рис. 5. Определение точки минимума целевой функции

Подставляя координаты точки минимума в целевую функ-цию, определяем ее оптимальное (минимальное) значение, которое равно 0.
Ответ: при заданных ограничениях минимальное значение целевой функции F(Х)=0, которое достигается в точке О (0; 0).

Пример 6.3. Решить следующую задачу ли-нейного программирования геометрическим методом:

Решение:

Рассматриваемая задача линейного программирования задана в канонической форме, выделим в качестве базисных переменные x 1 и x2.

Составим расширенную матрицу и выделим с помощью метода Жордана- Гаусса базисные переменныеx1 и x 2.

Сложим вторую с первой строкой:

В результате система ограничений примет следующий вид:

Выразим базисные переменные через свободные:

Выразим целевую функцию также через свободные перемен-ные, для этого подставим полученные значения базисных переменных в целевую функцию:

Запишем полученную задачу линейного программирования:

Так как переменные x1 и x2 неотрицательные, то полученную систему ограничений можно записать в следующем виде:

Тогда исходную задачу можно записать в виде следующей эк- вивалентной ей стандартной задаче линейного программирования:

Данная задача имеет два проектных параметра, следовательно, возможно ее решение геометрическим мето-дом.

1 этап: построение прямых, ограничивающих область допустимых решений ( ОДР).

Рассмотрим систему ограничений задачи линейного програм-мирования (для удобства пронумеруем неравенства):

Построим прямые, соответствующие каждому неравенству (рис. 6). Прямые пронумеруем согласно принятой ранее схе-ме.

2 этап: определение решения каждого из нера-венств системы ограничений.

С помощью контрольных точек определим полуплоскости – решения каждого из неравенств, и пометим их на графике (рис. 6) с помощью стрелок.

3 этап: определение ОДР задачи линейного про- граммирования.

Найденные полуплоскости (т.е. решения каждого из неравенств системы ограничений) не имеют общего пересечения (так решения неравенства I противоречат в целом остальным неравенствам системы ограничений), следовательно, система ограничений не совместна и задача линейного программирования в силу этого не имеет решения.

Рис. 6. Фрагмент MathCAD-документа:

построение области допустимых решений задачи

Ответ: рассматриваемая задача линейного программирования не имеет решения в силу несовместности системы ограничений.

Если после подстановки координат контрольной точки в неравенство его смысл нарушается, то решением данного неравенства является полуплоскость не содержащая данную точку (т.е. расположенная по другую сторону прямой).

Направление, обратное вектору-градиенту, соответствует направлению минимизации целевой функции.

Итак, пусть решается двумерная задача линейного программирования: требуется найти максимальное значение целевой функции

I

Предположим, что система ограничений (4.14) совместна, а область допустимых решений ограничена (рис. 4.1).

Решения каждого неравенства (4.14) образуют полуплоскость с границей а_пх_х + a_i2x₂ = b₍ (или х, = 0, х₂ = 0), и пересечение этих полуплоскостей образует многоугольник решений системы (4.14). Он на рис. 4.1 заштрихован.

Придадим целевой функции L(x) некоторое значение /₀, т.е. положим L(x) = l_Q.

Определение 4.4. Прямая

получаемая из (4.13) при фиксированном значении целевой функции, называется линией уровня (линией одинаковых значений целевой функции).

В дальнейшем при исследовании поведения целевой функции важную роль будет играть вектор

называемый градиентом целевой функции Цх).

Нетрудно проверить, что градиент совпадает с вектор-нормалью прямой (4.15), т.е. gradL(x) = (c_l,c₂) = n.

Теорема 4.1. Целевая функция L(x) возрастает при перемещении ее линии уровня по направлению вектора-градиента этой функции.

? На рис. 4.2 изображены градиент целевой функции и две ее линии уровня, соответствующие двум ра зличным значенииям параметра /: /, и /₂. Поскольку векторы п и MN коллинеарны и одинаково направлены, то их скалярное произведение положительно:

[it, MN) = c_x (х<'

х<) + с₂ (*2 - *2) > 0. Отсюда следует, что qx<'+ С₂х 2 - <с_хх[ + С₂х 2 ) = 1₂-1> 0, или /₂ > 1у ?

Из этой теоремы непосредственно получаем следующий геометрический способ построения оптимальных решений задачи линейного программирования.

• 1. Используя систему ограничений, строят многоугольник допустимых решений.
• 2. Проводят градиент целевой функции и одну из ее линий уровня.
• 3. Перемещают линию уровня в положительном направлении вектора-градиента и фиксируют два ее крайних положения, в которых она касается многоугольника допустимых решений (на рис. 4.1 это точки Ли/)). Именно эти точки касания и являются оптимальными решениями задачи линейного программирования (4.13)—(4.14): в точке А целевая функция имеет минимум, а в точке D — максимум.

Пример 4.1. Для изготовления двух видов мебели фабрика применяет древесину четырех видов. Их запасы ограничены и составляют соответственно 60, 80, 60,40 ед. Количество единиц древесины каждого вида, используемое для изготовления единицы каждого вида продукции, а также прибыль, получаемая от реализации единицы продукции, известны и приведены в табл. 4.3.

Требуется составить такой план выпуска продукции, который бы обеспечивал фабрике наибольшую прибыль от реализации всей продукции.

? Пусть вектор х = (х,, х₂) выражает планируемый объем выпуска мебели. От реализации такого объема продукции фабрика получит прибыль

при условии, что составляющие плана Xj и х₂ будут удовлетворять ограничениям

Таким образом, для сформулированной экономической задачи построена ее математическая модель (4.17)—(4.18), которая представляет собой типичную задачу линейного программирования. Для ее решения используем геометрический метод. На рис. 4.3 изображены многоугольник допустимых решений этой задачи (он заштрихован) с угловыми точками 0(О;О), Л(40;0), 7?(40;20), С(20;30), Д0;30), линия уровня Xj + 1,5х₂ = 0 и градиент п = (1; 1,5) целевой функции (4.17). Линия уровня при движении вдоль градиента дважды касается многоугольника допустимых решений: в точке О(0;0) (в этой точке целевая функция имеет минимум, равный нулю) и в точке (40;20), в которой она достигает своего максимального значения, равного Д40;20) = 40 + 1,5-20 = 70 ден. ед.

Таким образом, х, = 40 и х₂ = 20 является оптимальным планом выпуска мебели фабрикой, при котором она получит максимальную прибыль, равную 70 ден. ед. ?

2°. Геометрические методы также применимы и к решению многомерных задач линейного программирования, удовлетворяющих условию п — г 2) — число переменных, а г = rang(fl..) = т — ранг системы ограничений (см. формулу (4.14)*).

Используя преобразование Жордана—Гаусса, приведем задачу (4.10)*—(4.12)* к виду

где система ограничений имеет уже разрешенный вид. Поскольку последняя система ограничений равносильна к системе неравенств с двумя переменными (см. п. 4.4)

то первоначальная задача (4.10)*—(4.12)* будет эквивалентна решению следующей двумерной задачи линейного программирования:

изученной в предыдущем пункте.

В качестве иллюстрации вышеуказанного метода рассмотрим конкретный пример.

Пример 4.2. Решить геометрическим методом задачу

? Поскольку для этой задачи п — г= 5 — 3 = 2, то для ее решения применим вышеуказанный геометрический метод. Сначала, используя преобразования Жордана—Гаусса, систему ограничений задачи (одновременно и целевую функцию) запишем в разрешенном виде (основные расчетные работы приведены ниже в таблице):

Затем, отбрасывая в полученной системе ограничений разрешенные неизвестные, мы получим равносильную двумерную задачу линейного программирования:

Ниже на рис. 4.4 изображены: четырехугольник ABCD допустимых решений задачи (он заштрихован), градиент п = (3;0) и линия уровня х₄ = —2 целевой функции.

Из рисунка непосредственно следует, что оптимальным решением двумерной задачи является точка В(6;0). В этой точке целевая функция имеет максимум L(6;0) = 3-6 + 1-2 = 30. А чтобы найти оптимальное решение исходной задачи, воспользуемся формулами (*):

Решение задач линейного программирования

Формы задач линейного программирования

Стандартная задача линейного программирования:

Стандартная задача имеет важное значение ввиду того, что большое число прикладных моделей сводится именно к этому классу задач линейного программирования.

Каноническая задача линейного программирования:

Основные вычислительные методы (симплекс-метод и его модификации) решения задач линейного программирования разработаны именно для канонической задачи.

Общая задача линейного программирования:

Рассмотреть другие варианты…

Рассмотрим пример. Найти все возможные группы базисных переменных в системе

В задачах линейного программирования особый интерес представляют допустимые базисные решения, или т.н. опорные планы.

Пример. Найти все базисные решения следующей системы:

Геометрический смысл задачи линейного программирования

Рассмотрим следующую задачу линейного программирования:

Геометрическая интерпретация решения:

Рис. 1. Геометрическая интерпретация решения экстремальной задачи

Можно показать, что если задача линейного программирования имеет решение, то оно соответствует хотя бы одной угловой точке многогранника решений и совпадает, по крайней мере, с одним из допустимых базисных решений системы ограничений. Поэтому для решения задачи линейного программирования необходимо перебрать конечное число базисных решений, выбрать среди них то, на котором целевая функция принимает экстремальное значение. Геометрически это соответствует перебору всех угловых (крайних) точек многогранника. Если оптимальное решение существует, то такой перебор приведет к нахождению оптимального решения. Однако такой прямой перебор связан с очень большим объемом вычислений. Число перебираемых допустимых базисных решений можно сократить, если производить перебор не произвольно, а добиваясь того, чтобы каждое последующее решение было бы не хуже предыдущего. Такой подход, хотя и не исключает теоретической возможности перебора всех угловых точек, на практике позволяет существенно сократить число шагов при отыскании экстремума. Поясним это на графическом примере (см. рис. 2).

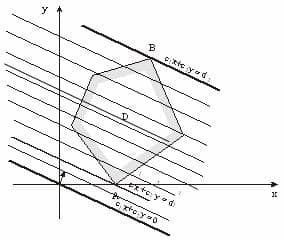
Пусть область допустимых решений изображается многоугольником ABCDEFGH. Пусть угловая точка B соответствует исходному допустимому базисному решению. При произвольном переборе всех вершин мы могли бы исследовать все семь вершин многогранника. В то же время видно, что после точки B выгоднее перейти к точке C, а затем к точке D, которая и будет оптимальной, т.е. вместо семи точек перебрали только три.

Идея последовательного улучшения решения легла в основу симплексного метода, наиболее часто применяемого метода решения задач линейного программирования.

Рис. 2. Область допустимых решений

Геометрический смысл симплексного метода состоит в том, что осуществляется последовательный переход от одной вершины многогранника ограничений к другой, соседней, в которой линейная функция принимает значение не худшее, чем в предыдущей. Эта процедура продолжается до тех пор, пока не будет найдено оптимальное решение. Симплексный метод, позволяющий решать любую задачу линейного программирования, универсален. В настоящее время он используется в программном обеспечении для решения задач линейного программирования на компьютере. Для решения задач небольшой размерности он может использоваться вручную.

Симплексный метод состоит из трех основных элементов:

1) определения какого-либо первоначального допустимого базисного решения;

2) правила перехода к лучшему решению;

3) проверки оптимальности допустимого решения.

Для использования симплексного метода задача линейного программирования должна быть приведена к каноническому виду, т.е. система ограничений должна быть представлена не в виде неравенств, а в виде равенств.

Дата добавления: 2019-03-09 ; просмотров: 268 ;