Метод корреляционно-регрессионного анализа шпора

французского кристаллографа Огюста Браве, немецкого физика Густава Теодора Фехнера, английского экономиста и статистика Фрэнсиса Эджуорта, впервые высказывавших в середине—конце XIX в. идеи о количественном измерении связей явлений. В разное время над теорией анализа работали известные в области теоретической статистики ученые Карл Фридрих Гаусс (Германия), Адриен Мари Лежандр (Франция), Карл Пирсон (Англия) и др.

Корреляционно-регрессионный анализ состоит в построении и анализе экономико-математической модели в виде уравнения регрессии (корреляционной связи), характеризующего зависимость признака от определяющих его факторов.

Корреляционно-регрессионный анализ предполагает следующие этапы:

• предварительный анализ (здесь формулируются основные направления всего анализа, определяется методика оценки результативного показателя и перечень наиболее существенных факторов);

• сбор информации и ее первичная обработка;

• построение модели (один из важнейших этапов);

• оценка и анализ модели.

Задачи корреляционного анализа сводятся к выделению важнейших факторов, которые влияют на результативный признак, измерению тесноты связи между факторами, выявлению неизвестных причин связей и оценке факторов, оказывающих максимальное влияние на результат.

Задачи регрессионного анализа заключаются в установлении формы зависимости, определении уравнения регрессии и его использовании для оценки неизвестных значений зависимой переменной, прогнозировании возможных значений результативного признака при задаваемых значениях факторных признаков.

При использовании корреляционно-регрессионного анализа необходимо соблюдать следующие требования.

1. Совокупность исследуемых исходных данных должна быть однородной и математически описываться непрерывными функциями.

2. Все факторные признаки должны иметь количественное (цифровое) выражение.

3. Необходимо наличие массовости значений изучаемых показателей.

4. Причинно-следственные связи между явлениями и процессами могут быть описаны линейной или приводимой к линейной формой зависимости.

5. Не должно быть количественных ограничений на параметры модели связи.

6. Необходимо обеспечить постоянство территориальной и временной структуры изучаемой совокупности.

Корреляция - статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.

В статистике принято различать следующие варианты зависимостей.

1. Парная корреляция - связь между двумя признаками (результативным и факторным).

2. Частная корреляция - зависимость между результативным и одним из факторных признаков при фиксированном значении других факторных признаков.

3. Множественная корреляция - зависимость результативного и двух или более факторных признаков, включенных в исследование.

Корреляционная связь - частный случай стохастической связи и состоит в том, что разным значениям одной переменной соответствуют различные средние значения другой.

Обязательное условие применения корреляционного метода - массовость значений изучаемых показателей, что позволяет выявить тенденцию, закономерность развития, форму взаимосвязи между признаками. Тогда, в соответствии с законом больших, чисел, влияние других факторов сглаживается, нейтрализуется. Наличие корреляционной связи присуще многим общественным явлениям.

Показатели тесноты связи между признаками называют коэффициентами корреляции. Их выбор зависит от того, в каких шкалах измерены признаки. Основными шкалами являются:

1) номинальная шкала (наименований) предназначена для описания принадлежности объектов к определенным социальным группам (например, коэффициенты ассоциации и контингенции, коэффициенты Пирсона и Чупрова);

2) шкала порядка (ординальная) применяется для измерения упорядоченности объектов по одному или нескольким признакам (например, коэффициенты Спирмена и Кенделла);

3) количественная шкала используется для описания количественных показателей — например, линейный коэффициент корреляции и корреляционное отношение.

Корреляционный анализ - метод статистического исследования экспериментальных данных, позволяющий определить степень линейной зависимости между переменными.

Парная линейная корреляция - простейшая система корреляционной связи, представляющая линейную связь между двумя признаками. Ее практическое значение состоит в выделении одного важнейшего фактора, который и определяет вариацию результативного признака.

Для определения степени тесноты парной линейной зависимости служит линейный коэффициент корреляции, который был впервые введен в начале 1890-х гг. Пирсоном, Эджуортом и Велдоном. В теории разработаны и на практике применяются различные варианты формул расчета данного коэффициента:

где n — число наблюдений.

При малом числе наблюдений для практических вычислений линейный коэффициент корреляции удобнее исчислять по формуле:

где r принимает значения в пределах от -1 до 1.

Степень взаимного влияния факторов в зависимости от коэффициента корреляции приведена в табл. 1.

Количественная оценка тесноты связи

при различных значениях коэффициента корреляции

Величина коэффициента корреляции	0,1-0,3	0,3-0,5	0,5-0,7	0,7-0,9	0,9-0,99
Теснота связи	Слабая	Умеренная	Заметная	Высокая	Весьма высокая

После того, как с помощью корреляционного анализа выявлено наличие статистических связей между переменными и оценена степень их тесноты, обычно переходят к математическому описанию зависимостей, то есть к регрессионному анализу.

Поскольку рост потомства стремится двигаться к среднему, Гальтон назвал это явление регрессией к среднему состоянию, а линию, проходящую через точки на графике, — линией регрессии.

Регрессивный анализ применяется в тех случаях, когда необходимо отыскать непосредственно вид зависимости х и у. При этом предполагается, что независимые факторы не случайные величины, а результативный показатель у имеет постоянную, независимую от факторов дисперсию и стандартное отклонение.

Одна из проблем построения уравнения регрессии — размерность, то есть определение числа факторных признаков, включаемых в модель. Их число должно быть оптимальным.

Сокращение размерности за счет исключения второстепенных, несущественных факторов позволяет получить модель, быстрее и качественнее реализуемую. В то же время построение модели малой размерности может привести к тому, что она будет недостаточно полно описывать исследуемое явление или процесс в единой системе национального счетоводства.

При построении модели число факторных признаков должно быть в 5-6 раз меньше объема изучаемой совокупности.

Если результативный признак с увеличением факторного признака равномерно возрастает или убывает, то такая зависимость является линейной и выражается уравнением прямой.

Линейная регрессия сводится к нахождению уравнения вида:

где х - индивидуальное значение факторного признака; а₀, а₁ - параметры уравнения прямой (уравнения регрессии); у_х - теоретическое значение результирующего фактора.

Данное уравнение показывает среднее значение изменения результативного признака х на одну единицу его измерения. Знак параметра показывает направление этого изменения. На практике построение линейной регрессии сводится к оценке ее параметров а₀, а_1.

При классическом подходе параметры уравнения а₀, а₁ находятся методом наименьших квадратов, который позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от расчетных, теоретических (у_х) была бы минимальной.

Для нахождения минимума данной функции приравняем к нулю частные производные и тем самым получим систему двух линейных уравнений, которая называется системой нормальных уравнений:

В уравнении прямой параметр а₀ экономического смысла не имеет, параметр а₁ является коэффициентом регрессии и показывает изменение результативного признака при изменении факторного на единицу.

Или по следующим формулам:

Между линейным коэффициентом корреляции и коэффициентом регрессии существует определенная зависимость, выраженная формулой

Часто исследуемые признаки имеют разные единицы измерения, поэтому для оценки влияния факторного признака на результативный применяется коэффициент эластичности. Он рассчитывается для каждой точки и в среднем по всей совокупности по формуле:

где у'_х — первая производная уравнения регрессии.

Коэффициент эластичности показывает, на сколько процентов изменяется результативный признак при изменении факторного признака на 1%.

Чтобы иметь возможность судить о сравнительной связи влияния отдельных факторов и о тех резервах, которые в них заложены, должны быть вычислены частные (средние) коэффициенты эластичности.

Частные коэффициенты эластичности показывают, на сколько процентов в среднем изменяется анализируемый показатель с изменением на 1 % каждого фактора при фиксированном положении других факторов.

Альтернативным показателем степени зависимости между двумя переменными является линейный коэффициент детерминации, представляющий собой квадрат линейного коэффициента корреляции r 2 . Его числовое значение всегда заключено в пределе от 0 до 1. Он характеризует долю вариации (разброса) зависимой переменной. Значение коэффициента детерминации непосредственно указывает степень влияния независимого фактора на результативный показатель.

Степень тесноты связи полностью соответствует теоретическому корреляционному отношению, которое является универсальным показателем тесноты связи по сравнению с линейным коэффициентом корреляции.

С помощью теоретического корреляционного отношения измеряется теснота связи любой формы, а посредством линейного коэффициента корреляции — только прямолинейной связи.

Теоретическое корреляционное отношение рассчитывается по формулам:

Для упрощения расчетов меры тесноты корреляционной связи часто применятся индекс корреляционной связи, который определяется по формулам:

Линейные модели отличаются простой интерпретируемостью и хорошо разработанными приемами оценивания коэффициентов регрессии. Обычно для них все три наиболее распространенных метода статистического оценивания - максимального правдоподобия, наименьших квадратов и моментов - дают оптимальные решения и соответственно приводят к оценкам, обладающим линейностью, эффективностью, несмещенностью. Принимая во внимание, что линейные регрессионные модели не могут с одинаково высокой степенью достоверности описывать многообразные процессы, происходящие в реальности, их дополняет большой класс нелинейных моделей. Для последних, однако, с учетом их сложности и специфичности приемов параметрического оценивания предпочтительным остается приведение к простой линейной форме.

Корреляционно-регрессионный анализ предполагает следующие этапы:

• предварительный анализ (здесь формулируются основные направления всего анализа, определяется методика оценки результативного показателя и перечень наиболее существенных факторов);
• сбор информации и ее первичная обработка;
• построение модели (один из важнейших этапов);
• оценка и анализ модели.

Задачи регрессионного анализа заключаются в установлении формы зависимости, определении уравнения регрессии и его использования для оценки неизвестных значений зависимой переменной, прогнозировании возможных значений результативного признака при задаваемых значениях факторных признаков.

При использовании корреляционно-регрессионного анализа необходимо соблюдать следующие требования:

1. Совокупность исследуемых исходных данных должна быть однородной и математически описываться непрерывными функциями.
2. Все факторные признаки должны иметь количественное (цифровое) выражение.
3. Необходимо наличие массовости значений изучаемых показателей.
4. Причинно-следственные связи между явлениями и процессами могут быть описаны линейной или приводимой к линейной форме зависимости.
5. Не должно быть количественных ограничений на параметры модели связи.
6. Необходимо обеспечить постоянство территориальной и временной структуры изучаемой совокупности.

Корреляция — статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.

Примеры корреляционной связи: рост и масса человека; цена и выручка от продажи; число членов семьи и жилая площадь и т. д.

В статистике принято различать следующие варианты зависимостей.

1. Парная корреляция — связь между двумя признаками (результативным и факторным).
2. Частная корреляция — зависимость между результативным и одним из факторных признаков при фиксированном значении других факторных признаков.
3. Множественная корреляция — зависимость результативного и двух или более факторных признаков, включенных в исследование.

Корреляционная связь — частный случай стохастической связи и состоит в том, что разным значениям одной переменной соответствуют различные средние значения другой.

Обязательное условие применения корреляционного метода — массовость значений изучаемых показателей, что позволяет выявить тенденцию, закономерность развития, форму взаимосвязи между признаками. Тогда в соответствии с законом больших чисел влияние других факторов сглаживается, нейтрализуется. Наличие корреляционной связи присуще многим общественным явлениям.

1) номинальная шкала (наименований) предназначена для описания принадлежности объектов к определенным социальным группам (например, коэффициенты ассоциации и контингенции, коэффициенты Пирсона и Чупрова);
2) шкала порядка (ординальная) применяется для измерения упорядоченности объектов по одному или нескольким признакам (например, коэффициенты Спирмена и Кенделла);
3) количественная шкала используется для описания количественных показателей — например, линейный коэффициент корреляции и корреляционное отношение.

Корреляционный анализ — метод статистического исследования экспериментальных данных, позволяющий определить степень линейной зависимости между переменными.

Парная линейная корреляция — простейшая система корреляционной связи, представляющая линейную связь между двумя признаками. Ее практическое значение состоит в выделении одного важнейшего фактора, который и определяет вариацию результативного признака.

Для определения степени тесноты парной линейной зависимости служит линейный коэффициент корреляции, который был впервые введен в начале 1890-х гг. Пирсоном, Эджуортом и Велдоном. В теории разработаны и на практике применяются различные варианты формул расчета данного коэффициента:

где п — число наблюдений;

При малом числе наблюдений для практических вычислений линейный коэффициент корреляции удобнее исчислять по следующей формуле:

Линейный коэффициент корреляции принимает значения:

Чем ближе линейный коэффициент корреляции по абсолютной величине к 1, тем теснее связь. С другой стороны, если он равен 1, то зависимость является не стохастической, а функциональной.

Степень взаимного влияния факторов в зависимости от коэффициента корреляции приведена в табл. 10.1.

Таблица 10.1. Количественная оценка тесноты связи при различных значениях коэффициента корреляции

Корреляционно-регрессионный анализ – это один из самых распространенных методов изучения отношений между численными величинами. Его основная цель состоит в нахождении зависимости между двумя параметрами и ее степени с последующим выведением уравнения. Например, у нас есть студенты, которые сдали экзамен по математике и английскому языку. Мы можем использовать корреляцию для того, чтобы определить, влияет ли успешность сдачи одного теста на результаты по другому предмету. Что касается регрессионного анализа, то он помогает предсказать оценки по математике, исходя из баллов, набранных на экзамене по английскому языку, и наоборот.

Что такое корреляционная диаграмма?

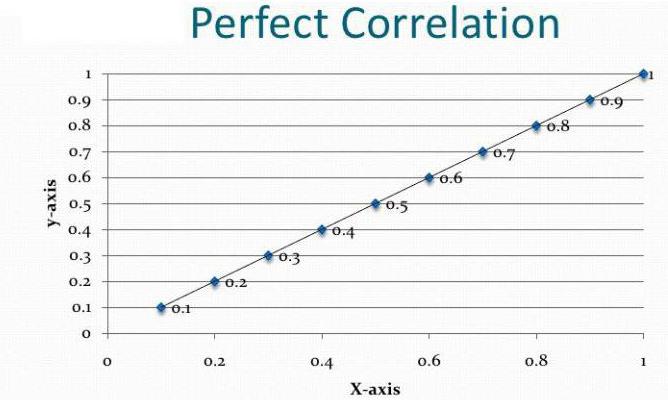
Любой анализ начинается со сбора информации. Чем ее больше, тем точнее полученный в конечном итоге результат. В вышеприведенном примере у нас есть две дисциплины, по которым школьникам нужно сдать экзамен. Показатель успешности на них – это оценка. Корреляционно-регрессионный анализ показывает, влияет ли результат по одному предмету на баллы, набранные на втором экзамене. Для того чтобы ответить на этот вопрос, необходимо проанализировать оценки всех учеников на параллели. Но для начала нужно определиться с зависимой переменной. В данном случае это не так важно. Допустим, экзамен по математике проходил раньше. Баллы по нему – это независимая переменная (откладываются по оси абсцисс). Английский язык стоит в расписании позже. Поэтому оценки по нему – это зависимая переменная (откладываются по оси ординат). Чем больше полученный таким образом график похож на прямую линию, тем сильнее линейная корреляция между двумя избранными величинами. Это означает, что отличники в математике с большой долей вероятности получат пятерки на экзамене по английскому.

Допущения и упрощения

Метод корреляционно-регрессионного анализа предполагает нахождение причинно-следственной связи. Однако на первом этапе нужно понимать, что изменения обеих величин могут быть обусловлены какой-нибудь третьей, пока не учтенной исследователем. Также между переменными могут быть нелинейные отношения, поэтому получение коэффициента, равного нулю, это еще не конец эксперимента.

Линейная корреляция Пирсона

Данный коэффициент может использоваться при соблюдении двух условий. Первое – все значения переменных являются рациональными числами, второе – ожидается, что величины изменяются пропорционально. Данный коэффициент всегда находится в пределах между -1 и 1. Если он больше нуля, то имеет место быть прямо пропорциональная зависимость, меньше – обратно, равен – данные величины никак не влияют одна на другую. Умение вычислить данный показатель – это основы корреляционно-регрессионного анализа. Впервые данный коэффициент был разработан Карлом Пирсоном на основе идеи Френсиса Гальтона.

Свойства и предостережения

Коэффициент корреляции Пирсона является мощным инструментом, но его также нужно использовать с осторожностью. Существуют следующие предостережения в его применении:

Коэффициент Пирсона показывает наличие или отсутствие линейной зависимости. Корреляционно-регрессионный анализ на этом не заканчивается, может оказаться, что переменные все-таки связаны между собой.
Нужно быть осторожным в интерпретировании значения коэффициента. Можно найти корреляцию между размером ноги и уровнем IQ. Но это не означает, что один показатель определяет другой.
Коэффициент Пирсона не говорит ничего о причинно-следственной связи между показателями.

Коэффициент ранговой корреляции Спирмана

Если изменение величины одного показателя приводит к увеличению или уменьшению значения другого, то это означает, что они являются связанными. Корреляционно-регрессионный анализ, пример которого будет приведен ниже, как раз и связан с такими параметрами. Ранговый коэффициент позволяет упростить расчеты.

Корреляционно-регрессионный анализ: пример

Предположим, происходит оценка эффективности деятельности десяти предприятий. У нас есть двое судей, которые выставляют им баллы. Корреляционно-регрессионный анализ предприятия в этом случае не может быть проведен на основе линейного коэффициента Пирсона. Нас не интересует взаимосвязь между оценками судей. Важны ранги предприятий по оценке судей.

Данный тип анализа имеет следующие преимущества:

Непараметрическая форма отношений между исследуемыми величинами.
Простота использования, поскольку ранги могут приписываться как в порядке возрастания значений, так и убывания.

Единственное требование данного типа анализа – это необходимость конвертации исходных данных.

Проблемы применения

В основе корреляционно-регрессионного анализа лежат следующие предположения:

Зависимость и причинно-следственная связь

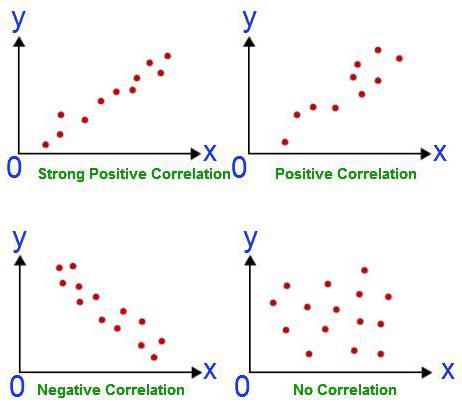
Предположим, мы вычислили коэффициент корреляции объема экспорта и ВВП. Он оказался равным единице по модулю. Провели ли мы корреляционно-регрессионный анализ до конца? Конечно же нет. Полученный результат вовсе не означает, что ВВП можно выразить через экспорт. Мы еще не доказали причинно-следственную связь между показателями. Корреляционно-регрессионный анализ – прогнозирование значений одной переменной на основе другой. Однако нужно понимать, что зачастую на параметр влияет множество факторов. Экспорт обуславливает ВВП, но не только он. Есть и другие факторы. Здесь имеет место быть и корреляция, и причинно-следственная связь, хотя и с поправкой на другие составляющие валового внутреннего продукта.

Гораздо опаснее другая ситуация. В Великобритании был проведен опрос, который показал, что дети, родители которых курили, чаще являются правонарушителями. Такой вывод сделан на основе сильной корреляции между показателя. Однако правилен ли он? Во-первых, зависимость могла быть обратной. Родители могли начать курить из-за стресса от того, что их дети постоянно попадают в переделки и нарушают закон. Во-вторых, оба параметра могут быть обусловлены третьим. Такие семьи принадлежат к низким социальным классам, для которых характерны обе проблемы. Поэтому на основе корреляции нельзя сделать вывод о наличии причинно-следственной связи.

Зачем использовать регрессионный анализ?

Корреляционная зависимость предполагает нахождение отношений между величинами. Причинно-следственная связь в этом случае остается за кадром. Задачи корреляционного и регрессионного анализа совпадают только в плане подтверждения наличия зависимости между значениями двух величин. Однако первоначально исследователь не обращает внимания на возможность причинно-следственной связи. В регрессионном анализе всегда есть две переменные, одна и которых является зависимой. Он проходит в несколько этапов:

Выбор правильной модели с помощью метода наименьших квадратов.
Выведение уравнения, описывающего влияние изменения независимой переменной на другую.

Например, если мы изучаем влияние возраста на рост человека, то регрессионный анализ может помочь предсказать изменения с течением лет.

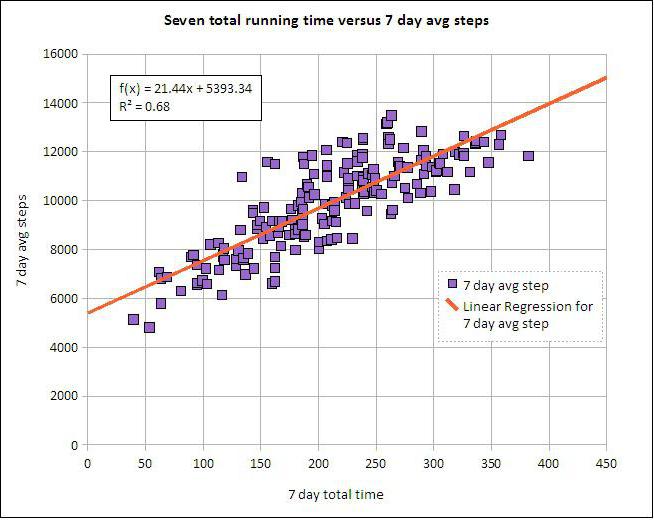
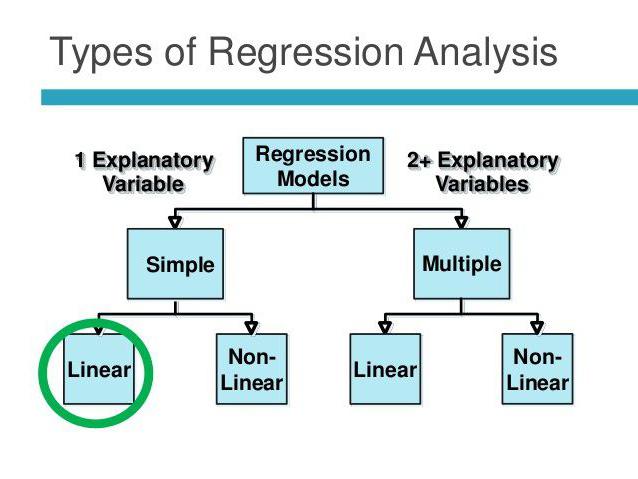
Линейная и множественная регрессия

Предположим, что X и Y – это две связанные переменные. Регрессионный анализ позволяет предсказать величину одной из них на основе значений другой. Например, зрелость и возраст – это зависимые признаки. Зависимость между ними отражается с помощью линейной регрессии. Фактически можно выразить X через Y или наоборот. Но зачастую только одна из линий регрессии оказывается правильной. Успех анализа во многом зависит от правильности определения независимой переменной. Например, у нас есть два показателя: урожайность и объем выпавших осадков. Из житейского опыта становится ясно, что первое зависит от второго, а не наоборот.

Множественная регрессия позволяет рассчитать неизвестную величину на основе значений трех и более переменных. Например, урожайность риса на акр земли зависит от качества зерна, плодородности почвы, удобрений, температуры, количества осадков. Все эти параметры влияют на совокупный результат. Для упрощения модели используются следующие допущения:

Зависимость между независимой и влияющими на нее характеристиками является линейной.
Мультиколлинеарность исключена. Это означает, что зависимые переменные не связаны между собой.
Гомоскедастичность и нормальность рядов чисел.

Применение корреляционно-регрессионного анализа

Существует три основных случая использования данного метода:

Тестирование казуальных отношений между величинами. В этом случае исследователь определяет значения переменной и выясняет, влияют ли они на изменение зависимой переменной. Например, можно дать людям разные дозы алкоголя и измерить их артериальное давление. В этом случае исследователь точно знает, что первое является причиной второго, а не наоборот. Корреляционно-регрессионный анализ позволяет обнаружить прямо-пропорциональную линейную зависимость между данными двумя переменными и вывести формулу, ее описывающую. При этом сравниваться могут величины, выраженные в совершенно различных единицах измерения.
Нахождение зависимости между двумя переменными без распространения на них причинно-следственной связи. В этом случае нет разницы, какую величину исследователь назовет зависимой. При этом в реальности может оказаться, что на их обе влияет третья переменная, поэтому они и изменяются пропорционально.
Расчет значений одной величины на основе другой. Он осуществляется на основе уравнения, в которое подставляются известные числа.

Таким образом корреляционный анализ предполагает нахождение связи (не причинно-следственной) между переменными, а регрессионный – ее объяснение, зачастую с помощью математической функции.

69. Теория игр, корреляционный, регрессионный, дисперсионный анализы

Теория игр исследует оптимальность стратегии в ситуациях игрового характера. Формализуя конфликтные ситуации математически, их можно представить как игру нескольких игроков, каждый из которых преследует цель максимизации своей выгоды, своего выигрыша за счет других. Решение

подобных задач требует определенности в формулировании их условий установления количества игроков, правил игры, выявления возможных стратегий игроков, возможных выигрышей. Для решения задач применяются алгебраические методы, основанные на системе линейных уравнений и неравенств, итерационные методы, а также приемы сведения задачи к некоторой системе дифференциальных уравнений.

Корреляционный анализ применяется в том случае, когда между отдельными признаками (показателями) имеется связь (зависимость). Этот метод дает возможность аналитически выразить форму (тенденцию) связи показателей, оценить ее тесноту. Регрессионный анализ представляет собой выведение уравнения регрессии, с помощью которого оценивается величина случайной переменной, если величина другой переменной (или других в случае множественной или многофакторной регрессии) известна (фиксирована, неслучайна). Регрессионные модели – статистические уравнения, составляемые для определения значений некоторых переменных и оценки их влияния на искомую величину.

Дисперсионный метод используется при анализе результатов наблюдений, зависящих от различных, одновременно действующих факторов. Метод чаще всего применяется при оценке влияния мероприятий, количественная оценка эффективности которых непосредственно затруднена. Дисперсионный метод оказывается весьма полезным для оценки эффективности новой системы управления, так, при этом важны не только показатели темпов роста за определенный период до и после осуществления анализируемого мероприятия, но и многие другие причины и обстоятельства, в том числе случайные, не поддающиеся учету.

Данный текст является ознакомительным фрагментом.

Читать книгу целиком