Реляционная алгебра и язык sql шпора
Реляциционная алгебра состоит из операций над отношениями и их составляющими (атрибутами и кортежами). Результат любой операции реляционной алгебры - новое отношение. Такие системы операций называются замкнутыми. Рассмотрим семь основных операций (рис. 1) реляционной алгебры. Они разделены на две группы. В первую входят операции, совершаемые над любыми множествами:
- объединение,
- пересечение,
- разность
- декартово произведение.
Во вторую группу входят операции, применимые только к отношениям:
- выборка,
- проекция,
- соединение.
| Рис. 1. Операции реляционной алгебры |
Объединение - операция над двумя отношениями, в результате которой получается новое отношение, состоящее из всех кортежей исходных отношений. Общие для исходных отношений кортежи в новом отношении встречются только по одному разу.
Реальный запрос на языке SQL состоит из двух объединённых операторов SELECT. Первым SELECT выбирается вся таблица (реальная, а не теоретическое отношение) Физ_лица, вторым - Юр_лица. Результаты обеих выборок выводятся в общую таблицу. Оба оператора объединяются в один запрос предложением UNION:
Пересечение - операция над двумя отношениями, в результате которой получается новое отношение, состоящее из кортежей, принадлежащих обоим исходным отношениям.
Разность - операция над двумя отношениями, в результате которой получается новое отношение, состоящее из кортежей, принадлежащих первому отношению и не принадлежащих второму.
Декартово произведение - операция над двумя отношениями, в результате которой получается новое отношение, состоящее из всех возможных кортежей, являющихся попарными сочетаниями кортежей исходных отношений.
Операции объединения, пересечения и разности имеют следующие особенности:
- участвующие в операции отношения должны иметь одинаковое количество атрибутов;
- попарно соответствующие атрибуты отношений должны иметь одинаковый тип;
- наименование каждого атрибута отношения-результата может быть либо новым, либо наследовать имя атрибута одного из исходных отношений.
Выборка производится над кортежами одного отношения. Результат выборки - новое отношение, состоящее из котежей исходного отношения, удовлетворяющих заданному условию.
На языке SQL запрос запрос выглядит так:
Проекция также производится над кортежами одного отношения. Результат проекции - новое отношение содержащее только заданные атрибуты исходного отношения.
На языке SQL запрос запрос выглядит так:
Язык SQL предназначен для работы с реальными таблицами и допускает несколько одинаковых строк в таблице с результатами запроса. Для исключения одинаковых строк служит служебное слово DISTINCT
Соединение - операция над двумя отношениями, имеющими общие атрибуты, в результате которой получается новое отношение, состоящее из всех атрибутов исходных отношений и объединяющее только те кортежи исходных отношений в которых значения общих атрибутов совпадают.
Семантически общие атрибуты описывают общие свойства соединяемых отношений. Общие атрибуты должны иметь один тип
Даны два отношения Рабочие и Инструменты
Нужно выбрать из обоих отношений сведения о рабочих и взятых ими инструментах. Общий атрибут - ТабНомер. В отношении Инструменты табельных номеров 3 и 4, нет, поэтому строки с этими номерами из отношения Рабочие в результаты запроса не попадут. На языке SQL запрос выглядит так:
Если в запросе не указать общий атрибут, то получится декартово произведение, состоящее из 4*5=20 кортежей.
При выполнении запроса SELECT, как правило, делаются несколько реляционных операций. Например, для выборки из отношения Рабочие всех кортежей со слесарями и атрибутов ФИО и Должность служит оператор
Выполнение этого запроса состоит из двух реляционных операций: выборки и проекции.
До сих пор мы рассматривали выбор информации из единственной таблицы. Можно запрашивать информацию из нескольких таблиц, реализуя описанные в соответствующем разделе учебника реляционные операции . Стоит упомянуть, что полное рассмотрение темы выходит за рамки данного учебника. Подробно этот вопрос можно изучить при помощи, например, [ [ 3.1 ] , [ 11.2 ] ]. Рассмотрим некоторые примеры того, как это делается.
Как правило, в тех случаях когда возникает необходимость выбирать информацию из разных таблиц, они тем или иным образом связаны друг с другом, например отношениями один к многим или один к одному по некоторому полю.
Еще раз вернемся к примеру из "Физические модели данных (внутренний уровень)" . Рассмотрим соответствующую ER-диаграмму ( рис. 12.2.).
В этом примере тоже присутствуют связанные таблицы. Рассмотрим таблицы student, mark_st и exam_st.
Таблица mark_st связана с таблицей exam_st по полю id_ex .
Таблица mark_st связана с таблицей student по полю id_st .
Допустим, требуется распечатать список студентов с оценками, которые они получили на экзаменах. Для этого необходимо выполнить следующий запрос :
Отметим следующие изменения по сравнению с запросами к одной таблице.
- В секции FROM указаны две таблицы.
- Так как таблиц стало больше одной, появилась некоторая неоднозначность при упоминании полей. Так, во многих случаях неизвестно, из какой таблицы из списка FROM брать поле. Для устранения неоднозначности имена полей указываются с префиксом – именем таблицы. Имя таблицы от имени поля отделяется точкой.
- В предложении WHERE указано условие соединения таблиц.
Нетрудно заметить, что использование префиксов-имен таблиц сильно загромождает запрос . Для того чтобы избежать подобного загромождения, используются псевдонимы. Так, можно переписать предыдущий запрос следующим образом:
Для добавления данных в таблицу в стандарте SQL предусмотрена команда INSERT . Рассмотрим ряд примеров запросов.
Данный запрос вставляет в таблицу mark_st строку, содержащую значения, перечисленные в списке VALUES . Если не нужно указывать значение какого-то поля, можно присвоить ему NULL :
В случае если необходимо использование для некоторых полей значений по умолчанию, SQL позволяет явно указать, какие поля необходимо заполнить конкретными данными, а какие – значениями по умолчанию:
Для удаления данных из таблицы существует команда DELETE :
Этот запрос удаляет все данные из таблицы student.
Можно ограничить диапазон удаляемой информации следующим образом:
Для обновления данных используется команда UPDATE .
При помощи этого запроса изменится на "5" оценка у студента с кодом 100 по экзамену с кодом 10.
Язык SQL является средством выражения мощного математического аппарата теории множеств и реляционной алгебры . В данном разделе рассматривается связь операторов языка SQL с операциями реляционной алгебры и теории множеств.
Средствами языка SQL операция объединения представляется следующим образом:
Средствами языка SQL операция разности представляется следующим образом:

Если 
– операция "=", то это эквисоединение.
Краткие итоги: В лекции дается общая характеристика операторов языка SQL , используемых, в частности, для работы с базой данных в интерактивном режиме (создание таблиц, выбор информации из таблиц, добавление, удаление и модификация элементов). Дается понятие интерактивного режима работы с SQL . Рассматриваются основные операторы SQL , используемые для манипулирования данными (выбор информации из таблиц, добавление, удаление и модификация элементов). Приводятся примеры записи запросов к базе данных на языке SQL с использованием операторов select, insert , update , delete . Рассматривается связь между операциями реляционной алгебры и операторами языка SQL .
Более подробно материалы лекции рассматриваются в [ [ 3.1 ] - [ 5.4 ] ].
Основы реляционной алгебры
Доступ к реляционным данным осуществляется при помощи реляционной алгебры. Основная идея реляционной алгебры состоит в том, что коль скоро отношения являются множествами, то средства манипулирования отношениями могут базироваться на традиционных теоретико-множественных операциях, дополненных некоторыми специальными операциями, специфичными для баз данных.
Рассмотрим вариант алгебры, который был предложен Коддом. Набор основных алгебраических операций состоит из восьми операций, которые делятся на два класса - теоретико-множественные операции и специальные реляционные операции. В состав теоретико-множественных операций входят операции:
· взятия разности отношений;
· прямого произведения отношений.
Специальные реляционные операции включают:
Операндами каждой такой операции является одно или несколько отношений, результатом выполнения операции всегда является новое отношение.
В рассмотренных ниже примерах используются следующие отношения:
P(D1,D2,D3) Q(D4,D5) R(M,P,Q,T) S(A,B)
1 11 x x 1 x 101 5 a 5 a
2 11 y x 2 y 105 3 a 10 b
3 11 z y 1 z 500 9 a 15 c
4 12 x w 50 1 b 2 d
· ОБЪЕДИНЕНИЕ
Отношения-операнды в этом случае должны быть определены по одной схеме. Результирующее отношение содержит все строки операндов, за исключением повторяющихся.
· ПЕРЕСЕЧЕНИЕ
На входе операции два отношения, определенные по одной схеме. На выходе - отношение, содержащие кортежи, которые присутствуют в обоих исходных отношениях.
· РАЗНОСТЬ
Операция, во многом похожая на ПЕРЕСЕЧЕНИЕ, за исключением того, что в результирующем отношении содержатся кортежи, присутствующие в первом и отсутствующие во втором исходных отношениях.
Входные отношения могут быть определены по разным схемам. Схема результирующего отношения включает все атрибуты исходных. Кроме того:
o степень результирующего отношения равна сумме степеней исходных отношений;
o мощность результирующего отношения равна произведению мощностей исходных отношений.
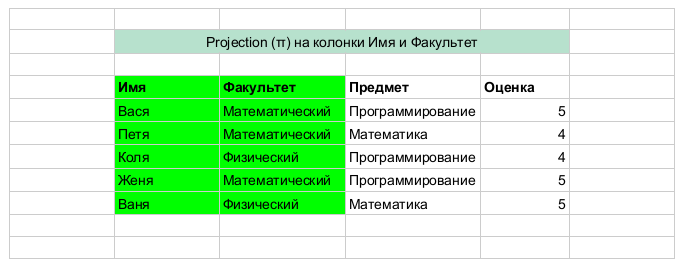
· ПРОЕКЦИЯ (ВЕРТИКАЛЬНОЕ ПОДМНОЖЕСТВО)
Операция проекции представляет собой выборку из каждого кортежа отношения значений атрибутов, входящих в список A, и удаление из полученного отношения повторяющихся строк.
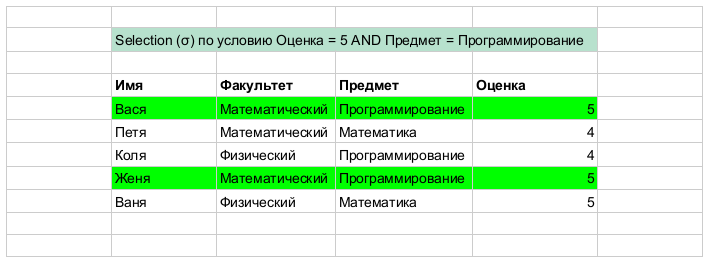
· ВЫБОРКА (ОГРАНИЧЕНИЕ, ГОРИЗОНТАЛЬНОЕ ПОДМНОЖЕСТВО)
На входе используется одно отношение, результат - новое отношение, построенное по той же схеме, содержащее подмножество кортежей исходного отношения, удовлетворяющих условию выборки.
· СОЕДИНЕНИЕ
Данная операция имеет сходство с ДЕКАРТОВЫМ ПРОИЗВЕДЕНИЕМ. Однако здесь добавлено условие, согласно которому вместо полного произведения всех строк в результирующее отношение включаются только строки, удовлетворяющие определенному соотношению между атрибутами соединения (А1,A2) соответствующих отношений.
Пусть отношение R , называемое делимым, содержит атрибуты (A1,A2. An). Отношение S - делитель содержит подмножество атрибутов A: (A1,A2. Ak)(k
Стандарт языка SQL, хотя и основан на реляционной теории, но во многих местах отходит он нее. Например, отношение в реляционной модели данных не допускает наличия одинаковых кортежей, а таблицы в терминологии SQL могут иметь одинаковые строки. Имеются и другие отличия.
Операторы SQL. Основу языка SQL составляют операторы, разбитые на две группы по общности выполняемых функцияй:
Операторы DDL (Data Definition Language) - операторы определения объектов базы данных:
· CREATE TABLE - создать таблицу,
· ALTER TABLE - изменить таблицу,
· DROP TABLE - удалить таблицу,
· CREATE DOMAIN - создать домен,
· ALTER DOMAIN - изменить домен,
· DROP DOMAIN - удалить домен,
· CREATE VIEW - создать представление,
· DROP VIEW - удалить представление.
Операторы DML (Data Manipulation Language) - операторы манипулирования данными:
· SELECT - отобрать строки из таблиц,
· INSERT - добавить строки в таблицу,
· UPDATE - изменить строки в таблице,
· DELETE - удалить строки в таблице,
· COMMIT - зафиксировать внесенные изменения,
· ROLLBACK - откатить внесенные изменения.
Любая операция реляционной алгебры может быть выражена одним оператором SELECT.
Последнее изменение этой страницы: 2016-12-16; Нарушение авторского права страницы
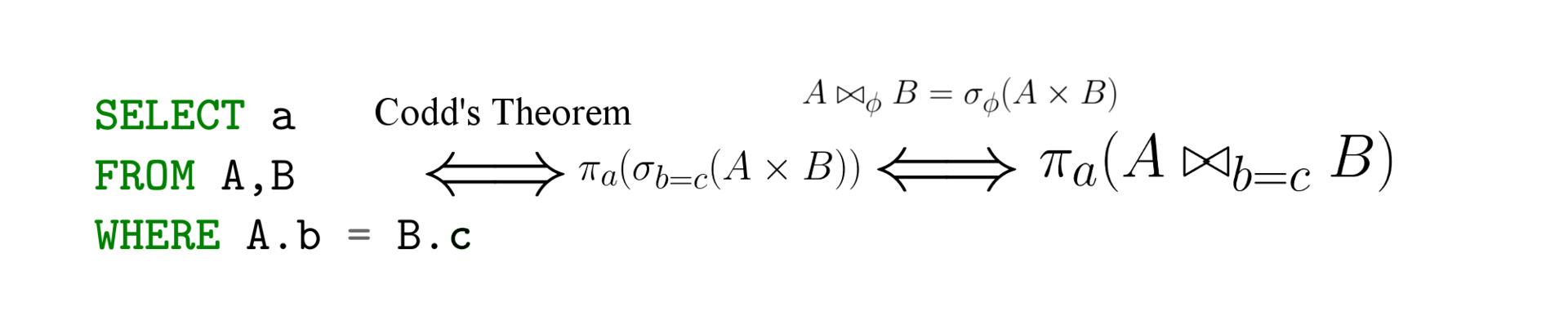
На Хабре и за его пределами часто обсуждают реляционную алгебру и SQL, но далеко не так часто акцентируют внимание на связи между этими формализмами. В данной статье мы отправимся к самым корням теории запросов: реляционному исчислению, реляционной алгебре и языку SQL. Мы разберем их на простых примерах, а также увидим, что бывает полезно переключаться между формализмами для анализа и написания запросов.
Зачем это может быть нужно сегодня? Не только специалистам по анализу данных и администраторам баз данных приходится работать с данными, фактически мало кому не приходится что-то извлекать из (полу-)структурированных данных или трансформировать уже имеющиеся. Для того, чтобы иметь хорошее представление почему языки запросов устроены определенным образом и осознанно их использовать нужно разобраться с ядром, лежащим в основе. Об этом мы сегодня и поговорим.
Большую часть статьи составляют примеры с вкраплениями теории. В конце разделов приведены ссылки на дополнительные материалы, а для заинтересовавшихся и небольшая подборка литературы и курсов в конце.
Основные операторы

Операции над множествами
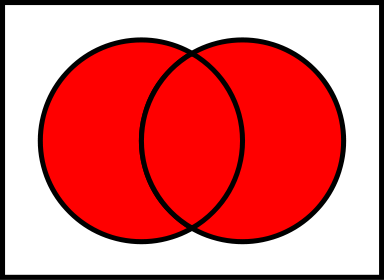
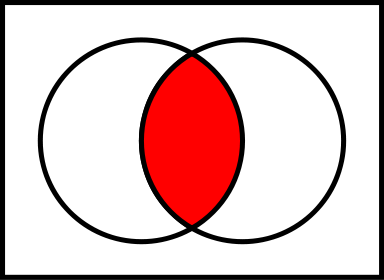
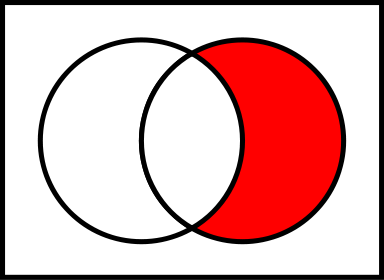
(B\A; A — слева, B — справа)

Задачи для разогрева
Мы будем работать со следующей схемой 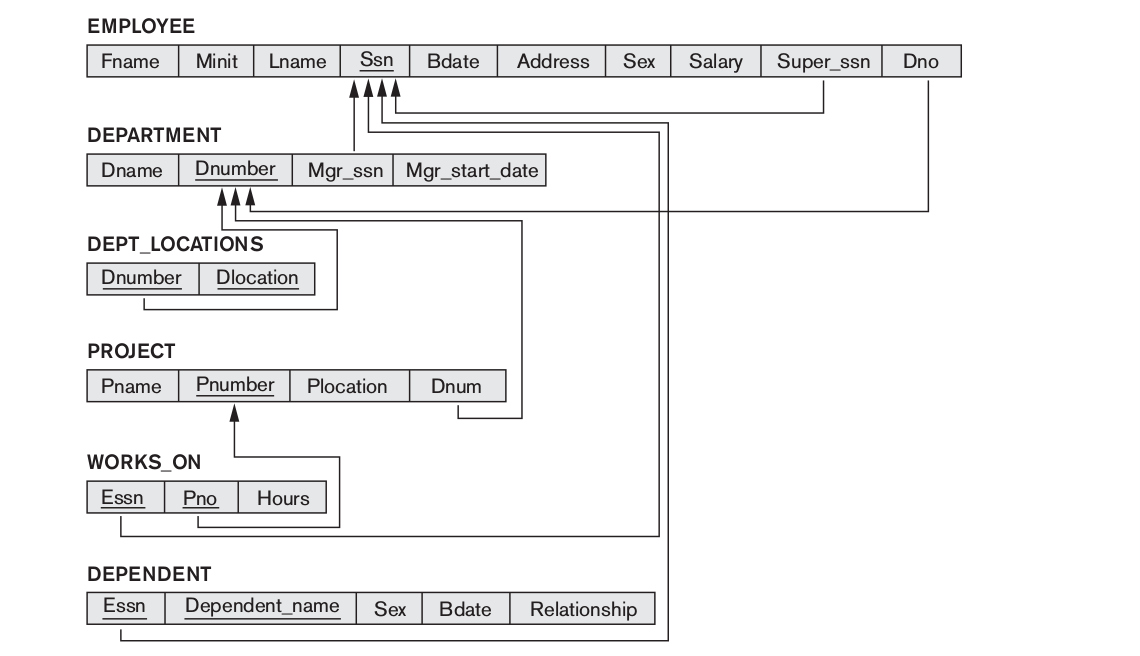
(Схема взята из книги: Elmasri, Navathe – Fundamentals of Database systems; на всякий: крайне НЕ рекомендую книгу; см подборку в конце)
Далее рассмотрим несколько простых задач на реляционную алгебру.
Задача первая. Вывести имена всех работников 5го департамента, которые работают более 10 часов в неделю над проектом Х.

Задача вторая. Вывести имена всех работников, которыми напрямую руководит Франклин Вонг (и найти небольшую ошибку в решении ниже)

Для каждого проекта вывести название и общее число часов в неделю, которое все работники тратят на этот проект.

Заметим, что запрос имеет вид a F b (A), где a, b — колонки, A — отношение, а – агрегационная функция (например, SUM, MIN, MAX, COUNT, etc). Читается следующим образом: для каждого значения в колонке а, посчитай b. То есть одному значению в колонке a может соотвестовать несколько строк, поместим значения колонки b из этого множества строк в функцию и создадим новый атрибут fun_b с соотвествующим значением.
Откуда в точности следует данные результат мы разберем позднее, сейчас можно лишь отметить, что запросы с агрегацией принадлежат более высокому классу вычислительной сложности.
Мы рассмотрим и проанализируем более интересные примеры задач далее в статье. Там же небольшая подборка задач на реляционную алгебру с решениями доступна здесь
В данной части мы поговорим о SQL (Structured Query Language) и покажем, как SQL соответствует реляционной алгебре на простых примерах.
Рассмотрим самую первую задачу еще раз:
Задача первая. Вывести имена всех работников 5го департамента, которые работают более 10 часов в неделю над проектом Х.
Классическое решение выглядит следующим образом:

Альтернативно можно написать вот так:

Или совсем альтернативно:

(далее решения не убраны под спойлеры)
На втором решении мы видим отчетливую аналогию c реляционной алгеброй:

Теперь используем равенство для join и увидим аналогию между SQL и реляционной алгеброй в первом решении

Как бы это не было иронично, но SELECT в SQL — это project (π; проекция) в реляционной алгебре.
Теперь рассмотрим задачу с агрегацией и сравним её с решением на реляционной алгебре:

Более интересные задачи мы рассмотрим далее в статье (также небольшая подборка здесь), а сейчас рассмотрим еще один формализм запросов.
Внимательный читатель сейчас мог бы воскликнуть: для чего козе баян? Нам тут что не хватает двух формализмов для написания запросов, к чему третий?
Реляционное исчисление — это адаптация логики первого порядка (FOL: first order logic) для написания запросов. FOL является одним из самых хорошо изученных формализмов математики и даёт возможность использовать уже созданный теоретический аппарат и классические результаты для анализа и написания запросов.
Многие результаты в сложности, (не)выразимости и формировании запросов пришли в базы данных из логики, именно благодаря реляционному исчислению, поэтому и стоит ознакомиться с данным формализмом.
Для разбора и рассказа о реляционном исчислении нам потребуется логика первого порядка, освежить знания о которой можно тут.
Пусть φ(Х) — формула первого порядка, а X — это свободные переменные, т.е., они не квантифицированы (∀ – квантор всеобщности, ∃ – квантор существования), тогда запрос в реляционном исчислении задает множество:
Рассмотрим простые примеры, на которых и разберем формализм:
Пусть R – отношение с тремя атрибутами a,b,c; тогда перепишем следующий запрос реляционной алгебры:
Переводя на простой язык r — это кортеж в R (то есть строка с атрибутами, значения которых можно получить через точку по имени, i.e., r.a — атрибут а кортежа r (строки) в отношении R (таблице)). Как мы видим никаких кванторов здесь нет, так как r — на выходе запроса и должен быть свободным кортежем.
Рассмотрим еще один простой пример: R(a,b,c) ∗ S(c,d,e), где * — это natural join, т.е. join по имени – в качестве условия объединения берут атрибуты с одинаковым именем.
Если бы s.D и S.e не было среди выходных параметров, запрос бы имел следующий вид:
Составляя подобные запросы всегда следует быть внимательным с квантором всеобщности, если мы запишем следующее выражение (исключительно в качестве иллюстрации):
Здесь можно найти краткую подборку задач на реляционное исчисление с решениями.
Говоря простым языком, теорема Кодда звучит так: все три формализма SQL, реляционная алгебра и реляционное исчисление равны. Вот тут много теории для заинтересовавшихся
То есть любой запрос выраженный на одном языке может быть переформулирован на другом. Данный результат прежде всего удобен тем, что позволяет использовать наиболее удобный формализм для анализа запроса, а во вторых он связывает декларативные языки SQL и реляционное исчисление с императивной реляционной алгеброй. То есть, транслируя запрос из SQL в реляционную алгебру, мы уже получаем способ выполнения запроса (и его оптимизации).
Запросы, которые состоят из select(σ)-project(π)-join(⋈) сегмента реляционной алгебры называют conjunctive queries (ок, я опустил переименование, считаем его неявно присутствующим).
Если вы дочитали до этой строки попробуйте решить следующую задачу используя только эти три оператора (ну и отношения конечно же):
Задача. Выведите имена всех работников, которые работают над каждым проектом.
Подумайте какому сегменту SQL и реляционного исчисления относится данный класс реляционной алгебры.
Существует несколько различных способов измерить вычислительную сложность выполнения запроса, между ними часто путаются поэтому выпишем определения и их названия:
Пусть Q — запрос, D — база данных, и нужно вычислить Q(D)
- Если Q — фиксировано, то сложность вычисления f(D) называется сложностью по данным (data complexity)
- Если D — фиксировано, то сложность вычисления f(Q) называется сложностью запроса (query complexity)
- Если ничего не фиксировано, то сложность f(Q,D) называют комбинированной сложностью (combined complexity)
Важные факты: сложность SQL по данным (и всех остальных) принадлежит классу AC0 – это очень хороший класс сложности, т.е., запросы можно вычислять очень эффективно.
С теоретической точки зрения можно взглянуть на вот эту картинку: 
Рассмотрим следующий интересный вопрос, связанный с вычислительной сложностью: пусть f – функция выполнимости формулы, то есть для каждого запроса она говорит, существует ли база данных такая, что Q(D) истинно. Из теоремы Кодда мы знаем, что реляционная алгебра и SQL эквиваленты реляционному исчислению. А значит, вычисление f – эквивалентно проблеме останова (SAT для логики первого порядка невычислим). Отсюда: не существуют алгоритма, который бы для произвольного SQL запроса мог определить его непротиворечивость.
Для заинтересовавшихся также рекомендую: теорема Трахтенброта
CQ являются одним из самых изученных классов запросов так как они составляют всю основную массу запросов к базам данных (я видел на одной презентации цифру в 90%, но не могу сейчас найти источник). Поэтому рассмотрим подробнее их сложность и докажем, что на самом деле их комбинированная сложность равна NP, т.е. задача является NP полной. (Про NP полному можно почитать вот тут и тут.)
Для этого запишем произвольный CQ запрос в реляционном исчислении в виде:
Чтобы показать, что задача принадлежит классу NP-полных, нужно сделать две вещи
- Показать, что задача внутри NP класса
- Показать, что NP полная задача сводится к данной
Покажем, что задача о раскраске графа сводится к задаче выполнимости CQ запроса.
Пусть D состоит из одного отношения edge = <(red,green),(green,red), (blue, red), (green,blue) … >— всех возможных правильных раскрасок графа, таких что никакие две вершины не имеют одинакового цвета.
Тогда, запишем следующий запрос
Вопрос со звёздочкой: из сегмента select-project-join выкидываем project, как изменится вычислительная сложность?
Определения сложности по данными и по запросу также проливают свет на один известный результат — в классическом SQL (без with) транзитивное замыкание невыразимо при фиксированном запросе т.е. нельзя написать один запрос такой, что для любой базы данных он вычислял бы замыкание предиката. То есть, если у нас есть граф сохраненный в виде отношения edge, то нельзя написать один фиксированный запрос, который бы для произвольного графа вычислял отношение достижимости. Хотя интуитивно кажется, что такой запрос явно должен лежать в классе СQ.
Доказательство нетривиально и его можно пропустить без потери понимания дальнейшего материала.
Теорема о компактности: бесконечное множество формул выполнимо (имеет модель — интерпретацию, в которой все формулы верны), тогда и только тогда когда любое конечное подмножество этого множества выполнимо.
Гёдель: логика первого порядка компактна.
Кодд: SQL — логика первого порядка
Доказательство от противного, пусть T(a,b) — есть путь из а в б. P_n(a,b) — это путь из а в b длины n. Тогда
P_n(a,b) — из а нет пути в b длины n.
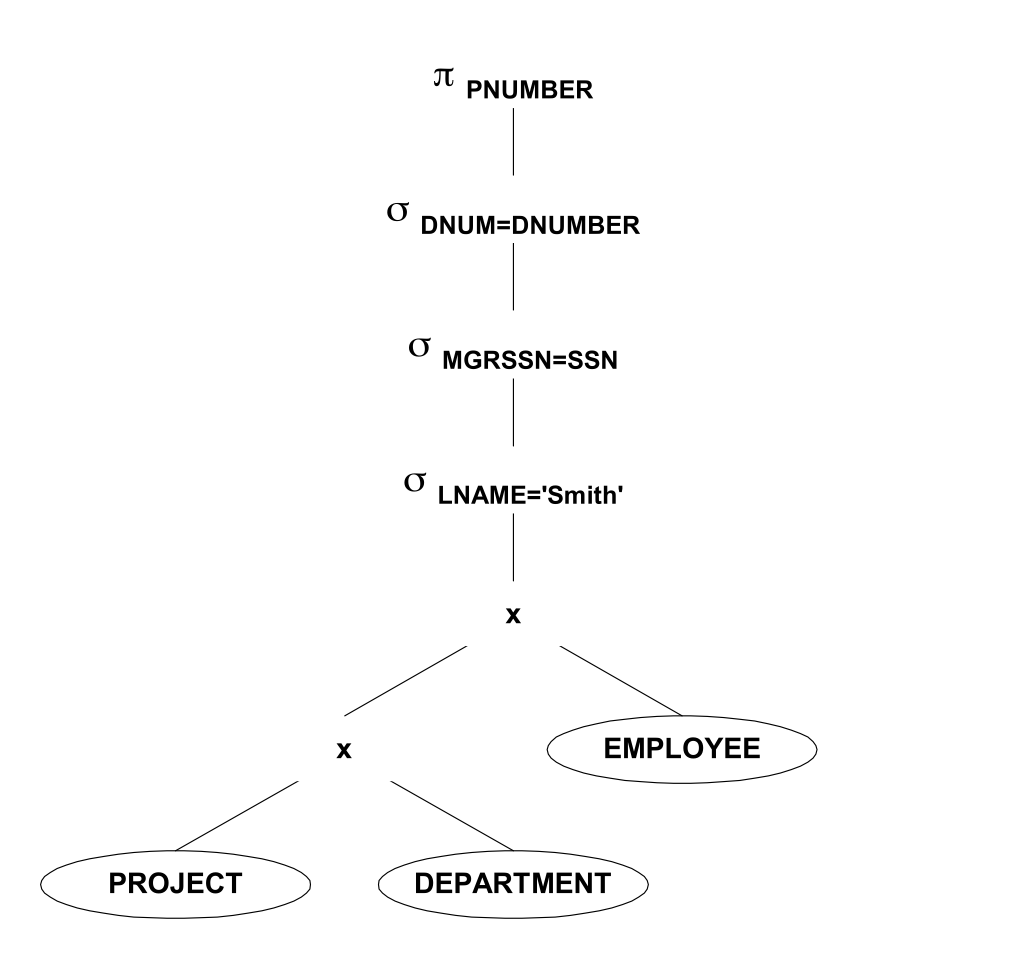
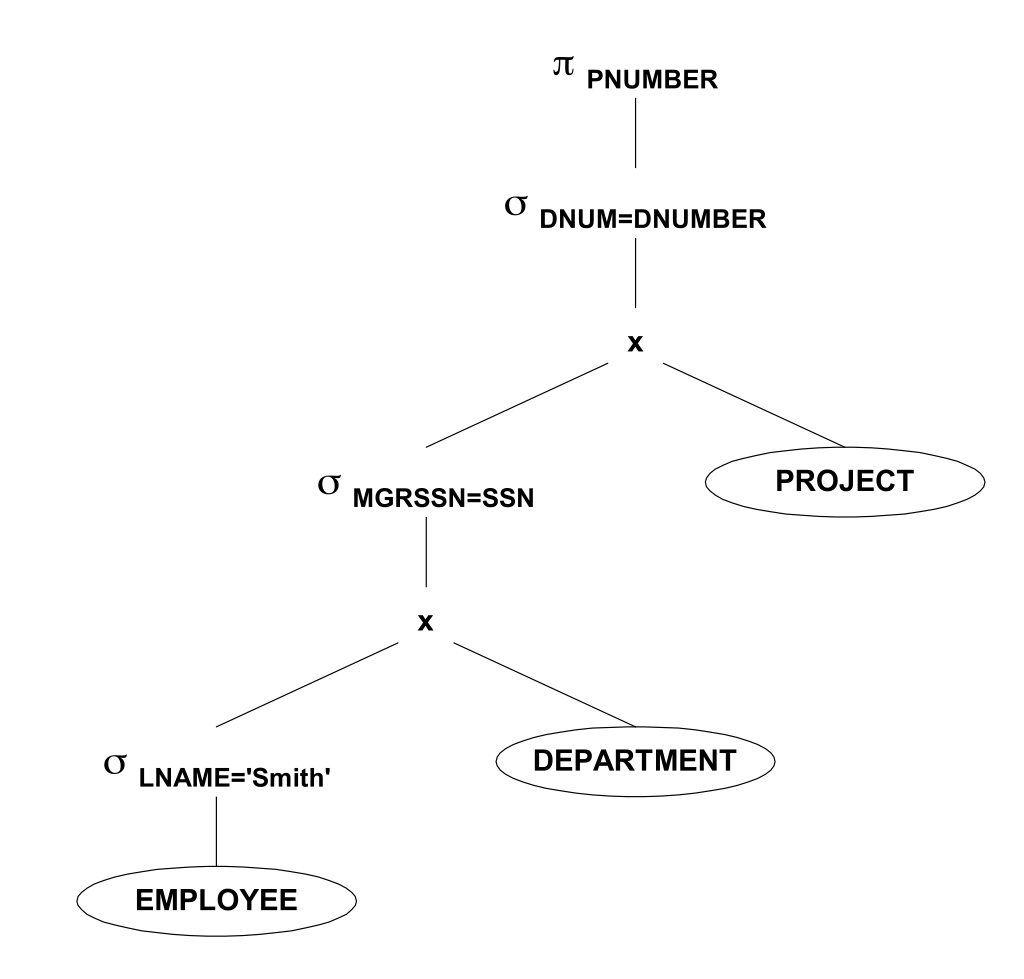
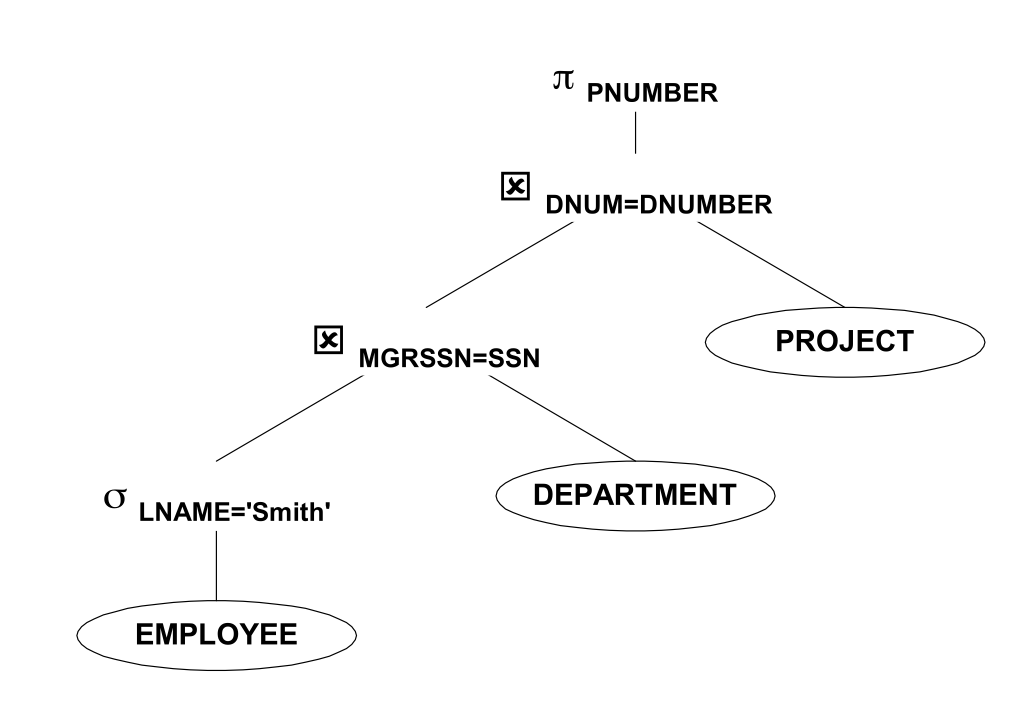
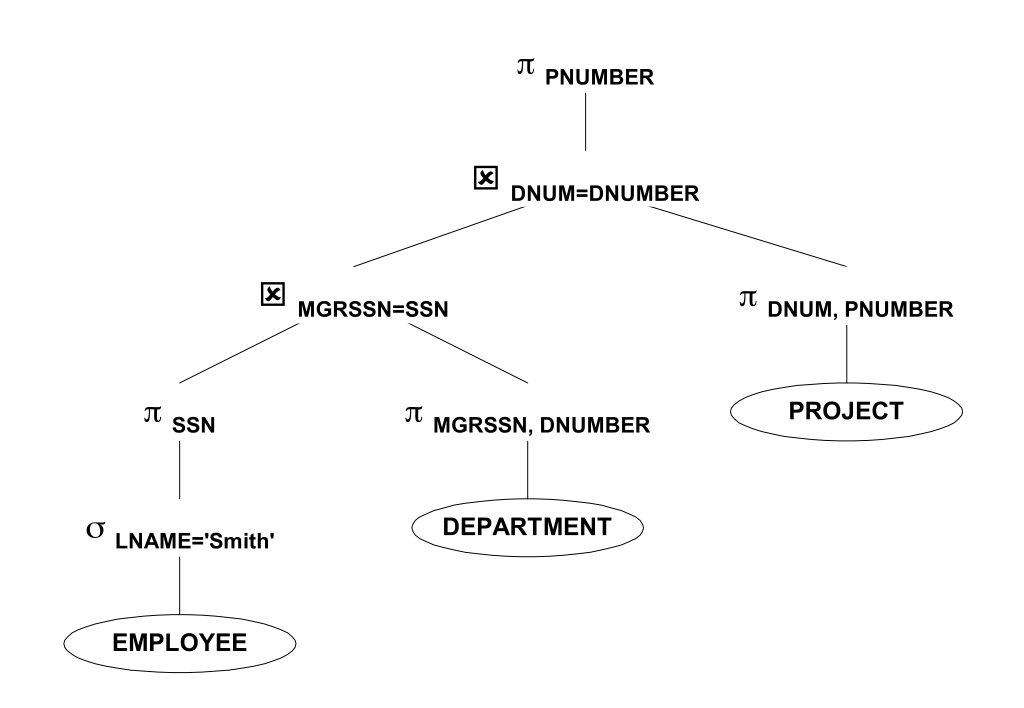
Возьмем следующее конечное множество P_k(a,b)> — оно выполнимо, так как возьмем путь длины k+1 и T(a,b) выполнено и все P_k тоже выполнены. Более того любое конечное множество такого вида выполнимо, а значит по теореме о компактности и их бесконечное объединение должно быть выполнимо. P_k — должно быть верно для ЛЮБОГО k, то есть не должно существовать пути никакой длины из а в b, а для выполнения T(a,b) такой путь должен существовать. Противоречие. Q.E.D. Если запрос не фиксирован, то задача становится тривиально разрешимой. Пусть у меня всего k ребер в базе данных, значит самый большой путь не более k, значит можно в явном виде записать запрос, как объединение путей длины 1, 2,… k и таким образом получить запрос вычисляющий достижимость в графе. Теперь вернемся к задаче предложенной ранее: Выведите имена всех работников, которые работают над каждым проектом. Почему эта задача не имеет решения в классе CQ мы можем понять, определив ключевые свойства самого запроса и класса CQ. Наблюдение: CQ — класс монотонно возрастающих запросов. Представим произвольный CQ запрос Q — он состоит из select-project-join. Покажем, что каждый из них является монотонным оператором: Пусть мы добавили еще одну запись в D select — фильтрует записи по вертикали, если новая запись удовлетворяет запросу, то множество ответов увеличивается, если нет остается прежним. project — не влияет на дополнительный кортеж join — если соответствующая запись имеется и во втором множестве, то ответное множество расширится, иначе останется прежним. Суперпозиция монотонных операторов монотонна => CQ — класс монотонных запросов. Вопрос: является ли исходная задача монотонной? На самом деле нет. Пусть у нас только один работник Петя, который работает над двумя проектами А и Б, и всего у нас 2 проекта А и Б, значит Петя должен быть в выдаче запроса. Пусть мы добавили третий проект C => теперь Пети нет в ответе и ответное множество пусто, а значит запрос не монотонен. Отсюда логически следует следующий вопрос: что нужно добавить к select-project-join, чтобы задача решалась? Это что-то должно быть немонотонным! Как конечно же читатель догадался — разница множеств. Его несимметричность как бы подсказывала нам и выделяла его с самого начала. Однако прежде, чем писать решение сделаем еще одно наблюдение: если контр-примера к утверждению не существуют, то это утверждение всегда верно. Формально: Также трансформация SQL в реляционную алгебру позволяет оптимизировать выполнение запроса. Рассмотрим простой пример: Задача Простое решение выглядит следующим образом: Которое можно переписать в реляционную алгебру следующим образом: Первая оптимизация — нужно использовать select как можно раньше, тогда Декартово произведение получит на вход отношения меньшего размера: Select c равенством константе сильное ограничение, поэтому его нужно вычислять и соединять как можно раньше: Сворачиваем Декартово произведение и select в join (который реализован эффективно с индексами и специализированными структурами данных) Опускаем project как можно ниже, чтобы только необходимая информация была передана наверх по дереву 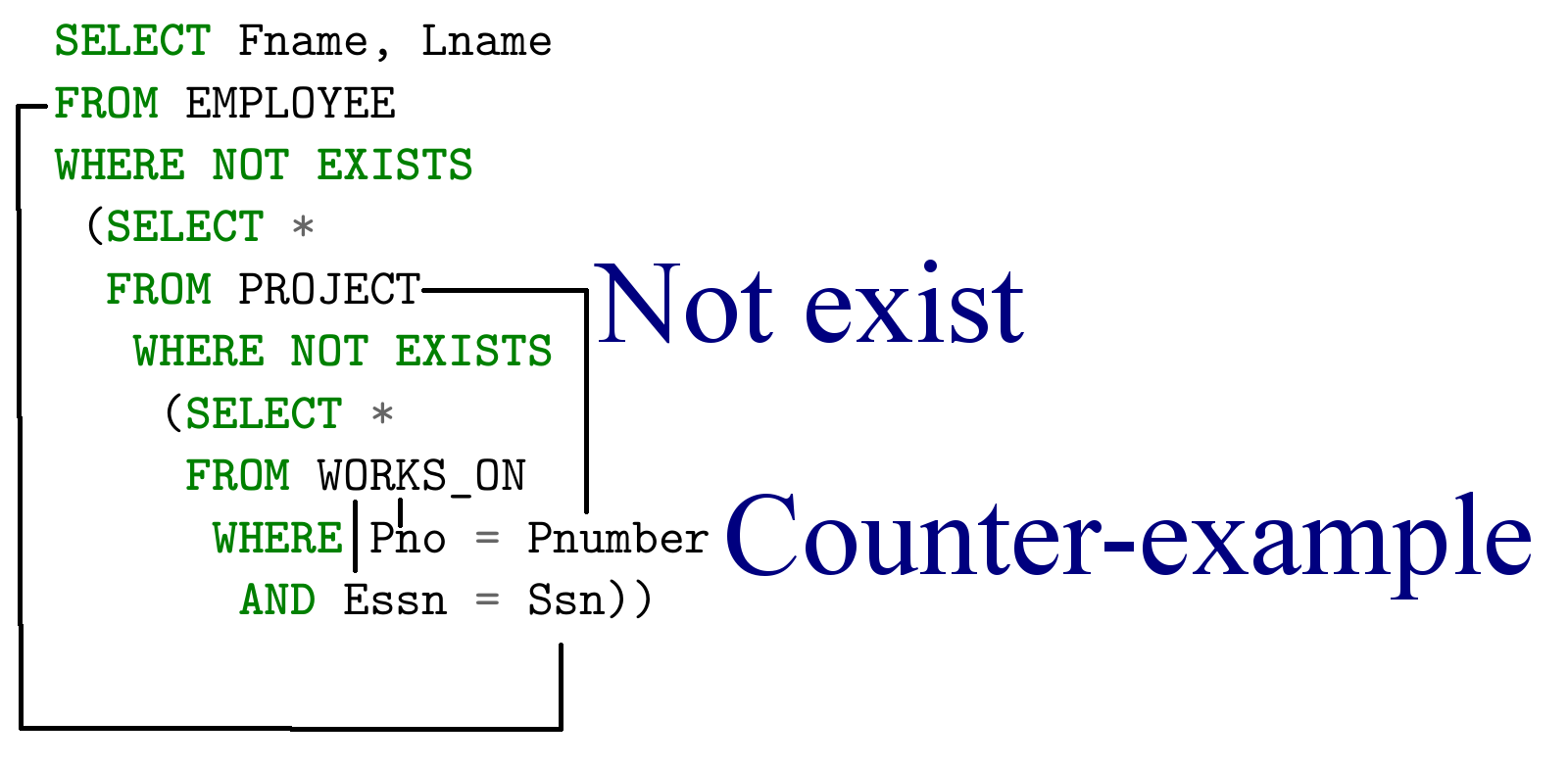
Вывести все номера проектов, в которых бы работал сотрудник с фамилией Шмидт в качестве менеджера департамента, управляющего этим проектом.

Читайте также:


