Пример операции Якобеуса. Эффективность операции Якобеуса
Добавил пользователь Валентин П. Обновлено: 28.01.2026
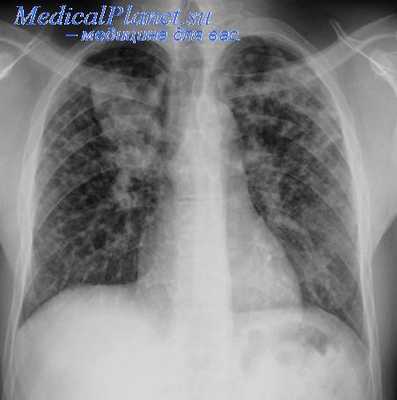
Подготовка к операции Якобеуса заключается прежде всего в постепенном доведении давления в плевральной полости до нуля, чтобы вскрытие ее не повлекло значительного изменения дыхания. Для этого увеличивают количество вводимого воздуха и частоту поддуваний, в течение 10—15 дней достигая выравнивания давления.
Если при этом больной испытывает тягостные ощущения или одышку, то операция откладывается до момента привыкания к большому коллапсу или вообще отменяется. Нужно, чтобы толщина слоя воздуха между грудной стенкой и легким была не менее 4 см. Если в плевральной полости имеется выпот, то стараются уменьшить его путем осторожных отсасываний с введением антибиотиков. При наличии других временных противопоказаний в предоперационном периоде пытаются ликвидировать их соответствующей терапией.
Для торакоскопии употребляются торакоскопы различной конструкции.
Торакоскоп с боковой оптикой создает видимость с углом зрения в 60°. Направление оптики отмечено на окуляре пуговкой. Недостатком этого то-ракоскопа является то, что при боковой оптике не видны предметы, расположенные впереди инструмента, искажается перспектива, т. е. отдаленные предметы кажутся слишком маленькими, а близко расположенные —слишком большими и, наконец, значительно искажается форма предмета. Преимуществом является возможность рассмотреть предметы, расположенные рядом с торакоскопом, а также возможность исследовать их со всех сторон при незначительном перемещении торакоскопа.
Торакоскоп с прямой оптикой позволяет видеть предметы в неискаженном виде, имеет угол зрения в 110°, но не дает возможности видеть предметы, расположенные рядом с торакоскопом. Обследование с помощью торакоскопа с прямой оптикой требует больших и неудобных его перемещений.
Инструмент, служащий для разрушения сращений, называется каутер. Он представляет собой изогнутый проводник, заканчивающийся на конце платиновой петлей. Каутер вводится вместе с футляром — тонкой трубкой, служащей проводником для каутера. Наконец, для прокалывания грудной стенки применяются специальные троакары, состоящие из стилета и канюли.
Подача тока для лампочки торакоскопа и для нагревания петли каутера осуществляется через обычный трансформатор, используемый для эндоскопии.
Стерилизация торакоскопов, каутеров и шнуров производится в парах формалина в закрытом сосуде или в спирте. Стилет, канюли и футляры стерилизуются кипячением. Торакоскопии производятся в затемненной операционной.
Пример операции Якобеуса. Эффективность операции Якобеуса
Комбинаторный метод анализа Якобеуса показывает довольно точные оценки вероятности потерь при малом числе звеньев. Покажем применение данного метода на примере двухзвенной коммутационной схемы с полнодоступным включением промежуточных линий (рис. 4.4).
Пусть на один из входов коммутатора первого звена двухзвенной схемы поступает заявка. Необходимо определить вероятность того, что она окажется необслуженной, т.е. вычислить потери. Анализ схемы рис. 4.4 показывает, что потери могут возникнуть в трех случаях:
1. Если заняты все выходов коммутатора первого звена, на который поступил вызов.
2. Если заняты все выходы коммутационной схемы.
3. Если свободные промежуточные линии не могут обеспечить соединение с выходами соответствующих коммутаторов второго звена из-за их занятости.
Таким образом, отказ в обслуживании возникает при одновременном появлении двух событий:
- заняты выходов из коммутатора, на вход которого поступил вызов;
- свободные промежуточные линии не могут обеспечить соединение со свободным выходом второго звена.
Метод Якобеуса предполагает, что события и независимы и потери при занятых выходах можно вычислить по формуле:
Так как в общем случае число занятых выходов, при поступлении вызова, может быть любым в пределах от до , то общие потери в двухзвенной коммутационной схеме определяются как
Вычислим вероятности и для примитивного потока заявок, поступающий на вход системы при равном числе входов и выходов коммутаторов первого звена и числе источников информации . Согласно формуле Энгеста, вероятность нахождения ровно заявок в системе равна
где - нагрузка входного потока от одного источника. Если ввести переменную
то формула (4.2) примет вид
где параметр имеет смысл вероятности занятости промежуточной линии между соответствующим выходом коммутатора перового звена и соответствующим входом коммутатора второго звена. Причем величина в то же время является средней интенсивностью нагрузки, обслуживаемой одной промежуточной линией.
Учитывая, что число свободных промежуточных линий равно , каждая из которых подключена к отдельному коммутатору второго звена, то вероятность можно определить как
где - средняя интенсивность обслуженной нагрузки всеми выходами коммутатора второго звена. Подставляя полученные выражения в формулу (4.1), получим выражение для общих потерь:
Рассмотрим другой случай работы двухзвенной схемы, когда число источников информации велико и входной поток заявок является простейшим. Время обслуживания одной заявки будем считать распределенным по показательному закону с параметром . Тогда вероятность занятости ровно выходов коммутатора первого звена можно вычислить по формуле Эрланга
где - величина нагрузки потока заявок на соответствующем выходе коммутатора первого звена.
Как правило, в системах с большим числом абонентов число коммутаторов первого велико и поток заявок в промежуточных линиях считается простейшим. При этом вероятность полагают равной средней интенсивности нагрузки , обслуженной соответствующей промежуточной линией. Так как свободных промежуточных линий , то вероятность их занятости
и величина потерь определяется по формуле
Рассмотрим работу двухзвенных схем, когда число входов больше числа выходов в коммутаторах первого звена. В таких системах возникают дополнительные потери при поступлении на вход коммутатора более вызовов.
Допустим, что число абонентов равно числу входов и входной поток заявок является примитивным. Вероятность поступления , , …, вызовов можно вычислить по аналогии с формулой (4.3), заменяя интенсивность потока интенсивностью потока обслуженных заявок одним входом коммутатора первого звена, т.к. в данном случае требуется оценить потери, возникающие из-за занятости всех выходов. Таким образом, потери можно записать в виде
Вероятности и определяются по формулам (4.3) и (4.4), т.к. остальные условия работы системы идентичны ранее рассмотренному случаю. В результате общие потери равны
При числе абонентов значительно больше числа входов двухзвенной системы и времени обслуживания, распределенным по показательному закону, вероятности и можно найти с помощью формулы Эрланга:
а вероятность определяется по формуле (4.5). Тогда общие потери определяются как
Представленные формулы расчета потерь справедливы и для двухзвенных схем, в которых выходы коммутатора первого звена соединены с входами коммутаторов второго звена не одной, а несколькими промежуточными линиями. В этом случае достаточно вместо значений , и подставить значения , и , где - число промежуточных линий, связывающие один выход коммутатора первого звена со входом коммутатора второго звена.
© 2022 Научная библиотека
Копирование информации со страницы разрешается только с указанием ссылки на данный сайт
Тема 9. Метод Якобеуса для расчета пропускной способности двухзвенных полнодоступных включений
Многозвенные коммутационные схемы имеют значительно большее число состояний, чем однозвенные. Поэтому система уравнений для вероятностей состояний многозвенной коммутационной схемы не только не может быть решена, но и во многих случаях не может быть записана.
Поэтому для расчета двухзвенных коммутационных схем при полнодоступном включении линий применяется приближенный комбинаторный метод Якобеуса.
Вызов в двухзвенной схеме может быть потерян в одном из трех случаев:
если заняты все промежуточные линии, которые могут быть использованы для обслуживания этого вызова;
если заняты все выходы в требуемом направлении;
если возникают неудачные комбинации свободных промежуточных линий и свободных выходов.
Вид формулы Якобеуса для вероятности потерь в двухзвенной коммутационной схеме при полнодоступном включении линий зависит от соотношения основных коммутационных параметров блока искания,
определяющих применение закона распределения вероятностей занятия обслуживающих устройств на первом и втором звеньях.
Примем следующие обозначения: - число входов в каждый коммутатор звена А;- число выходов из каждого коммутатора звена А;- коэффициент сжатия или расширения,;- число коммутаторов на звене А;- число выходов, выделяемых в направлении искания из каждого коммутатора звена В;-связность блока;- нагрузка на один вход;- нагрузка на одну промежуточную линию блока;- нагрузка на один выход в направлении искания;- интенсивность поступающей нагрузки в данном направлении (рис.9.1).
Мы считаем ранние сращения более легко пережигаемыми. Повышенная ваекуляризация сращений и их особая рыхлость наблюдались нами у 14% больных. Операции при ранних торакокаустиках, как мы видели из нашей статистики, не более опасны в смысле кровотечений, чем при поздних.
Неточность и произвольность понятия «ранняя» и «поздняя» торакокаустика с теоретической точки зрения доказываются на нашем материале тем, что у нас было 17 больных, у которых с момента выявления заболевания до наложения искусственного пневмоторакса прошло от 1 года до 10 лет.
Осложнений, которые могли бы быть связаны с близостью легочной ткани в коротких сращениях в плевре (ранение легкого, перфорация его, гнойные эмпиемы и т. п.), у наших больных не наблюдалось, что доказывает неосновательность доводов сторонников поздних торакокаустик и в данном вопросе.
Мы являемся сторонниками своевременного наложения искусственного пневмоторакса и возможно более быстрого исправления неэффективных пневмотораксов с учетом индивидуальных и клинических особенностей, показаний и противопоказаний к операции у каждого больного.
Выводы:
1. Раннее пережигание сращений не представляет большой опасности в отношении кровотечения, повреждения легочной ткани и увеличения плевральных осложнений.
2. Срок применения торакокаустики связан с возможностью безопасного введения инструментов в плевральную полость и манипуляций ими при операции.
3. При отсутствии видимых сращений и при наличии каверны необходим некоторый срок для выявления эффективности искусственного пневмоторакса.
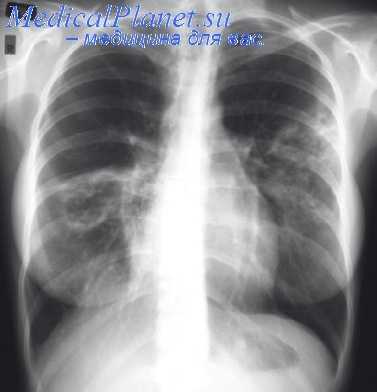
4. Всякое сращение, определяемое рентгенологически, является поводом для торакоскопии при отсутствии протвопоказаний к оперативному вмешательству со стороны общего состояния больного, состояния второго легкого, плевральной полости и функции диафрагмы на противоположной стороне.
5. При отсутствии противопоказаний торакоскопия должна применяться тогда, когда создан достаточный газовый пузырь и необходимое нулевое или близкое к нему давление.
6. Врач не должен быть связан искусственно созданными понятиями о «ранней» и «поздней» торакокаустике и широко применять ее, исходя из индивидуальных показаний у каждого больного.
Расширенное разрушение плевральных спаек
При современной комплексной терапии туберкулеза легких хирургическое лечение занимает одно из первых мест. Операция пережигания спаек, являясь самой распространенной, позволяет переводить целый ряд неэффективных пневмотораксов в эффективные. Непережигаемых сращений, по данным разных авторов, в среднем встречается до 70%, куда входят торакоскопии до 25% и частичные торакокаустики—до 45%. Пережиганию спаек методом Якобеуса подлежат лишь отдельные, растянутые до известной степени спайки, а не короткие, более массивные сращения.
В результате показатели эффективности этой операции (соотношение полных пережиганий спаек и частичных каустик и торакоскопии), несмотря на тонкую и высокую технику многих хирургов, остаются почти неизменными до последнего времени. Большинство авторов считает плевральные сращения короче 2 см непережигаемыми. Противопоказанными к пережиганию по вполне понятным причинам являются также короткие спайки, идущие к крупным сосудам (подключичная артерия, дуга аорты, верхняя полая вена и т. д.).
Абсолютно противопоказаны к пережиганию методом Якобеуса все плоскостные сращения, а также многие сращения с глубоким включением легочной ткани, доходящей до грудной стенки. Вопрос о возможности применения более расширенного разрушения спаек стал осуществим лишь с введением метода гидравлической препаровки и анестезии плевральных сращений, разработанного Л. К. Богушем в 1943 г. Этот хорошо известный метод Л. К. Богуша явился одним из способов эффективной борьбы с теми формами и видами плевральных сращений, которые недоступны методу Якобеуса.
Анализ и оптимизация коммутационных систем
Простейшая коммутационная система - это однофазная (однозвенная) схема, называемая коммутатором. Коммутатор имеет n входов и m выходов, каждый из которых может быть соединен с любым входом.
Рис. 2.1 Простейший коммутатор.
Выходы иногда объединяются в группы, которые определяют так называемые направления.
Коммутатор может быть неблокирующим, если выполнено соотношение n≤m , и блокирующим в противном случае. Блокируемость коммутатора определяется невозможностью части входов получить доступ ни к одному из выходов. Блокируемость может быть общей, когда все выходы рассматриваются равнозначными и блокируемость в определенном направлении, когда недоступными оказываются все выходы данного направления.
Важнейшей характеристикой коммутационной системы является число точек поля коммутации - управляемых точек соединения. Для коммутатора это число равно C= n x m .
Например для коммутатора 8x8 это число равно 64. Это означает, что реализующая этот коммутатор электрическая схема должна содержать 64 независимых контакта - электронных ключей. Для АТС на 10 000 абонентов реализация в виде простого коммутатора привела бы к необходимости построения схемы с 100.000.000 ключей.
В современной технике коммутационных систем применяются две основных технологии коммутации - пространственная и временная. Первая из них основана на реальных матрицах электронных ключей, а вторая использует временное мультиплексирование входных потоков и последующее перекрестное демультиплексирование. В любом случае число точек коммутации пространственных или временных ограничивается полупроводниковой технологией, возможностями теплоотвода и стоимостными факторами и требует снижения. В связи с этим для построения систем коммутации со многими входами и выходами применяют многозвенные схемы, которые позволяют обеспечить управляемое соединение входов и выходов используя меньшее чем в простом коммутаторе число точек коммутации.
Многозвенные системы кроме коммутаторов содержат фиксированные соединения между ними, называемые промежуточными линиями (ПЛ). Тем самым анализ многозвенных коммутационных схем относится к анализу сетей массового обслуживания и может проводиться описанными выше методами.
Здесь мы рассмотрим один специфический метод анализа, который применим при малом числе звеньев, но дает весьма точные результаты. Это комбинаторный метод Якобеуса. Покажем применение этого метода на примере двузвенной коммутационной системы с полнодоступным включением ПЛ.
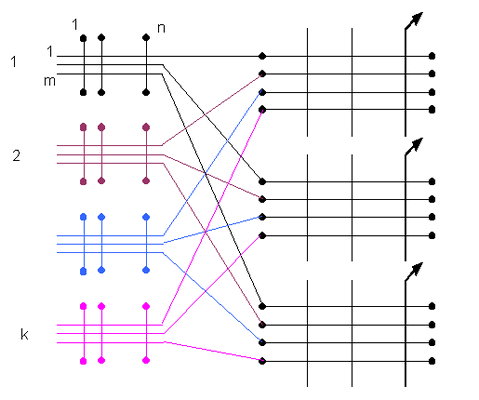
Рис. 2.2 Пример двузвенной коммутационной системы с полнодоступным включением ПЛ.
Число выходов из каждого коммутатора звена в этой схемe для направления с номером j равно единице. Будем считать, что к рассматриваемому моменту вызов поступил на один из входов схемы. Например, на второй вход первого коммутатора. Установление соединения через схему заключается в использовании одной из свободных ПЛ и одного из свободных выходов требуемого направления, взаимно доступных друг - другу. Для обслуживания поступившего вызова могут быть использованы m ПЛ и m выходов требуемого направления, выделенных на рисунке жирными линиями. Блокировка наступит в трех случаях:
1) заняты все ПЛ. которые могут быть использованы для обслуживания,
2) заняты все выходы в требуемом направлении,
3) комбинация свободных ПЛ и свободных выходов требуемого направления невзаимнодоступна.
Если вероятность занятия любых i из m промежуточных линий, принадлежащих коммутатору первого звена обозначить Wi , а вероятность занятия определенных m-i выходов (соответствующих свободным ПЛ) обозначить через Hm-i , то в соответствии со сказанным вероятность блокировки схемы может быть записана как
Метод Якобеуса предполагает, что события, определяемые этими вероятностями, независимы и могут быть заданы распределениями Эрланга или Бернулли.
При распределении Эрланга вероятность занятия i серверов в пучке из m серверов при интенсивности нагрузки на пучок равной А принимается равной
Вероятность занятия m-i фиксированных серверов из m серверов в пучке, была нами рассчитана также ранее:
Если использовать распределение Бернулли для задания вероятности любых i серверов из пучка из m устройств, то соответствующие вероятности могут быть определены как
Здесь в качестве ρ используется средняя нагрузка на одну линию в пучке.
Использование в формуле для вероятности блокировки этих различных распределений требует дополнительных предположений.
Если коммутаторы первого уровня имеют равное число входов и выходов ( схема без сжатия и расширения), то для ПЛ можно принять распределение Бернулли. Если для выходов двухзвенной схемы также принять распределение Бернулли, считая что число коммутаторов первого звена небольшое, то можно подсчитать вероятность блокировки схемы по формуле
Здесь приняты обозначения: b - средняя интенсивность нагрузки обслуживаемой одной ПЛ, Эрл, c - средняя интенсивность нагрузки, обслуживаемой одним выходом рассматриваемого направления, Эрл.
Если число коммутаторов первого звена достаточно велико, тогда целесообразно для выходов данного направления принять распределение Эрланга, Тогда подстановка в формулу вероятности блокировки дает
Если для образования каждого направления в каждом коммутаторе второго звена отводится не один, а q выходов, то для модели Бернулли для выходов можно получить формулу
Для модели Эрланга для выходовПри наличии сжатия в звене первого уровня можно считать пригодной модель Бернулли для первого звена и модель Эрланга для второго. Тогда вероятность блокировки может быть определена по формуле
В схемах с расширением, т.е. когда число выходов в коммутаторах первого звена превышает число входов, можно рассчитать вероятность блокировки по формуле
Здесь a обозначена средняя интенсивность нагрузки, обслуженной одним входом коммутатора первого звена.
Таким образом, мы получили ряд формул для расчета вероятности блокировки двухзвенной системы коммутации.
Теперь перейдем к анализу более сложных коммутационных схем. На практике в электронных системах часто используется трехзвенная схема коммутации, представленная на рис. 2.3.
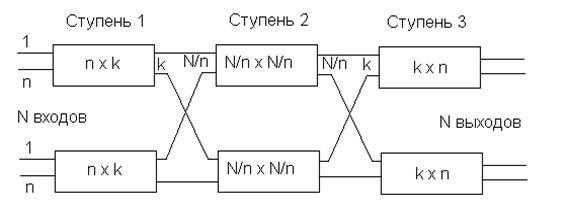
Рис. 2.3 Трехзвенная схема коммутации.
Схема содержит N/n входных и N/n выходных коммутаторов, образующих соответственно первую и третью ступени коммутации. Вторая ступень коммутации состоит из k квадратных коммутаторов с N/n входами и выходами. С помощью ПЛ каждый выход коммутатора первой ступени соединяется с разными коммутаторами второй ступени, так что подключаемый вход соответствует месту коммутатора первой ступени. Иначе говоря, выходы первого коммутатора первой ступени подключаются к первым входам коммутаторов второй ступени, выходы второго коммутатора - ко вторым входам всех коммутаторов второй ступени и так далее. Аналогично соединяются через ПЛ выходы коммутаторов второй ступени со входами коммутаторов третьей.
Если подсчитать число точек коммутации для этой схемы, то его можно выразить формулой
При надлежащем выборе параметров n и k сложность коммутационной схемы может быть существенно ниже, чем при однозвенном построении, когда число точек коммутации в точности равно NxN.
Давая выигрыш в числе точек коммутации, многозвенная схема может, как было показано на примере двухзвенной структуры, привести к наличию блокировок. Для трехзвенной схемы условие неблокируемости было получено Ч.Клосом:
k=2n-1.
Вывод этого соотношения проводится из простых рассуждений в предположении занятости n-1 входов коммутаторов первой и третьей ступени. Поскольку при этом будут заняты n-1 коммутаторов второй ступени, то для установления n -го соединения необходим еще один коммутатор второй ступени. Отсюда
k = (n-1)+(n-1)+1=2n-1 .
Число точек коммутации для неблокирующей трехзвенной схемы будет равно
Число коммутаторов в первой и третьей ступени также можно выбрать. Попытаемся минимизировать число точек коммутации, варьируя число входов n. Дифференцируя по n и решая уравнение, получим:
Очевидно, что это существенно меньше, чем NxN для однозвенной схемы. Например, при N=100 000 для однозвенной схемы число точек коммутации составило бы фантастическое число 10 10 . Для трехзвенной неблокирующей схемы оно составит около 1.7 10 8 . Еще большей экономии в сложности схемы можно достигнуть, применяя многозвенные схемы с блокировкой, но на очень низком уровне.
Для анализа таких схем применяют метод Якобеуса и более простой метод вероятностных графов Ли. Рассмотрим пример такого анализа для рассмотренной выше трехзвенной схемы.
Рис. 2.4 Граф Ли для трехзвенной схемы коммутации.
На рис. 2.4 представлен вероятностный граф, который отражает две группы каналов, которые должны соединяться друг с другом. Блокировка может возникнуть, если kn-1 . Кроме того, будем считать, что в системе не используется концентрация, т.е. k>n и блокировка входных или выходных коммутаторов исключена.
Предположим, что вероятность занятия входного канала равна значению параметра биноминального распределения, который, как показано было ранее, определяется через параметр входного потока и среднее время обслуживания
Предположим также, что нагрузка будет распределена равномерно между всеми коммутаторами промежуточного звена. Тогда вероятность занятия ПЛ будет равна
В соответствие с полученной выше формулой для графа Ли с параллельно-последовательной структурой можно записать:
Нужно сразу заметить, что эта вероятность не равна нулю даже при выполнении условия неблокируемости Клоса. Это говорит о погрешности формул, получаемых с помощью графов Ли.
Приведем таблицу для сравнения результатов расчета вероятности блокировки трехзвенной схемы методом графов Ли и метода Якобеуса.
| n | k | PB по Ли | PB по Якобеусу |
| 0.002 | 0.002 | ||
| 0.0002 | 0.00016 | ||
| 1.5x10 -5 | 6.2x10 -6 | ||
| 8x10 -7 | 1.5x10 -7 | ||
| 10 -7 | 3.5x10 -8 | ||
| 10 -14 | 1.3x10 -15 |
Из анализа полученных результатов видно, что метод Ли дает несколько завышенную оценку, особенно заметную для больших размеров коммутационной схемы.
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
© cyberpedia.su 2017-2020 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!
Читайте также:
