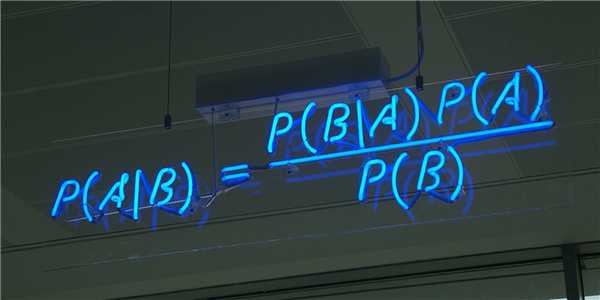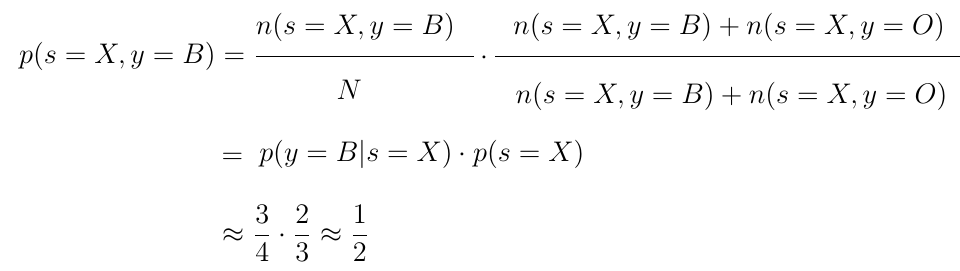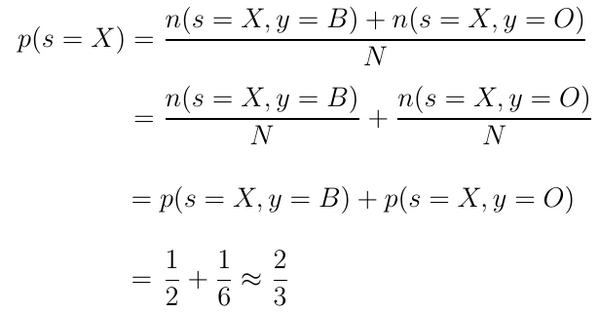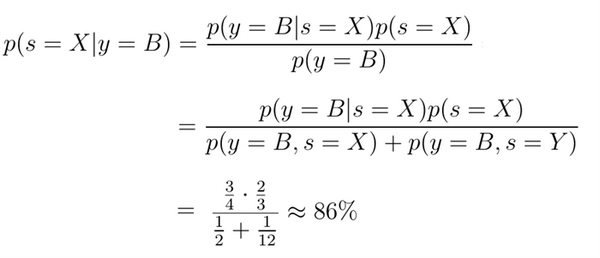Теорема Bayes. Отношение правдоподобия диагностических тестов

Добавил пользователь Евгений Кузнецов
Обновлено: 14.12.2024

Статистика играла ключевую роль в научном познании мира на протяжении веков, а в эпоху больших данных базовое понимание этой дисциплины и статистическая грамотность становятся критически важными. Дэвид Шпигельхалтер в своей книге «Искусство статистики. Как находить ответы в данных» приглашает вас в не обремененное техническими деталями увлекательное знакомство с теорией и практикой статистики, а мы публикуем главу из книги.

Сначала я должен сделать признание от имени всего статистического сообщества. Формальная основа для обучения на данных несколько запутанна. Несмотря на многочисленные попытки создать единую теорию статистических выводов, ни одна версия так и не была полностью принята. Неудивительно, что математики не любят преподавать статистику.

Мы уже познакомились с конкурирующими идеями Фишера и Неймана — Пирсона. Пришло время исследовать третий, байесовский подход к работе. Хотя он получил известность только в последнее пятидесятилетие, его базовые принципы восходят к далекому прошлому, фактически к преподобному Томасу Байесу, пресвитерианскому священнику и математику из Танбридж-Уэллса, занимавшемуся философией и теорией вероятностей.

Хорошая новость состоит в том, что байесовский подход открывает новые возможности для создания сложных данных.

Плохая — он означает, что вам придется отложить в сторону почти все, что вы узнали из этой и других книг об оценивании, доверительных интервалах, P-значениях, проверке гипотез и так далее.

В чем суть байесовского подхода?

Первым крупным вкладом Томаса Байеса в науку было использование вероятности как выражения недостатка наших знаний о мире или, что одно и то же, нашего незнания о происходящем в данный момент. Он показал, что вероятность может использоваться не только для будущих событий, подверженных случайности, — стохастической неопределенности, если пользоваться термином, введенным в главе 8, но и для реальных событий, хорошо известных некоторым людям, просто мы этого пока не знаем, то есть для эпистемической неопределенности. Если задуматься, то мы окружены эпистемической неопределенностью в отношении вещей, которые определены, но нам пока неизвестны. Игроки ставят на следующую карту, мы покупаем билеты мгновенной лотереи, обсуждаем пол будущего ребенка, ломаем голову над детективом, спорим о количестве тигров, оставшихся в дикой природе, и получаем оценки возможного числа мигрантов или безработных. Все это объективно существующие факты или числа, просто мы их не знаем. Снова подчеркну, что с байесовской точки зрения для представления нашего личного незнания этих фактов и чисел удобно использовать вероятности. Мы можем даже подумать о присвоении вероятностей альтернативным научным теориям, но этот вопрос более спорный. Конечно, эти вероятности будут зависеть от наших нынешних знаний: вспомните пример из главы 8, где вероятность выпадения орла или решки зависит от того, посмотрели мы на монету или нет. Байесовские вероятности с необходимостью субъективны — они зависят от наших отношений с окружающим миром, а не являются свойствами самого мира. Такие вероятности должны меняться по мере получения нами новой информации.

Это приводит нас ко второму крупному вкладу Байеса — результату, который позволяет постоянно пересматривать текущие вероятности в свете новых доказательств. Он известен как теорема Байеса и фактически предоставляет формальный механизм обучения на опыте — блестящее достижение для малоизвестного священника из маленького английского курортного городка.

Простое объяснение теоремы Байеса

Подробно теорема Байеса излагается в отдельной статье. Это замечательная работа, но в ней 15 000 слов. В этом же переводе статьи от Kalid Azad кратко объясняется самая суть теоремы.

Результаты исследований и испытаний - это не события. Существует метод диагностики рака, а есть само событие — наличие заболевания. Алгоритм проверяет, содержит ли письмо спам, но событие (на почту действительно пришел спам) нужно рассматривать отдельно от результата его работы.
В результатах испытаний бывают ошибки. Часто наши методы исследований выявляют то, чего нет (ложноположительный результат), и не выявляют то, что есть (ложноотрицательный результат).
С помощью испытаний мы получаем вероятности определенного исхода. Мы слишком часто рассматриваем результаты испытания сами по себе и не учитываем ошибки метода.
Ложноположительные результаты искажают картину. Предположим, что вы пытаетесь выявить какой-то очень редкий феномен (1 случай на 1000000). Даже если ваш метод точен, вероятнее всего, его положительный результат будет на самом деле ложноположительным.
Работать удобнее с натуральными числами. Лучше сказать: 100 из 10000, а не 1%. При таком подходе будет меньше ошибок, особенно при умножении. Допустим, нам нужно дальше работать с этим 1%. Рассуждения в процентах неуклюжи: «в 80% случаев из 1% получили положительный исход». Гораздо легче информация воспринимается так: «в 80 случаях из 100 наблюдали положительный исход».
Даже в науке любой факт — это всего лишь результат применения какого-либо метода. С философской точки зрения научный эксперимент - это всего лишь испытание с вероятной ошибкой. Есть метод, выявляющий химическое вещество или какой-нибудь феномен, и есть само событие — присутствие этого феномена. Наши методы испытаний могут дать ложный результат, а любое оборудование обладает присущей ему ошибкой.

Разберемся в методе

В статье, на которую дана ссылка в начале этого эссе, разбирается метод диагностики (маммограмма), выявляющий рак груди. Рассмотрим этот метод подробно.

1% всех женщин болеют раком груди (и, соответственно, 99% не болеют)
80% маммограмм выявляют заболевание, когда оно действительно есть (и, соответственно, 20% не выявляют)
9,6% исследований выявляют рак, когда его нет (и, соответственно, 90,4% верно определяют отрицательный результат)

1% женщин болеют раком груди
если у пациентки выявили заболевание, смотрим в первую колонку: есть 80% вероятность того, что метод дал верный результат, и 20% вероятность того, что результат исследования неправильный (ложноотрицательный)
если у пациентки заболевание не выявили, смотрим на вторую колонку. С вероятностью 9,6% можно сказать, что положительный результат исследования неверен, и с 90,4% вероятностью можно сказать, что пациентка действительно здорова.

Насколько метод точен?

Теперь разберем положительный результат теста. Какова вероятность того, что человек действительно болен: 80%, 90%, 1%?

Есть положительный результат. Разберем все возможные исходы: полученный результат может быть как истинным положительным, так и ложноположительным.
Вероятность истинного положительного результата равна: вероятность заболеть, умноженная на вероятность того, что тест действительно выявил заболевание. 1% * 80% = .008
Вероятность ложноположительного результата равна: вероятность того, что заболевания нет, умноженная на вероятность того, что метод выявил заболевание неверно. 99% * 9.6% = .09504

вероятность события = исходы события / все возможные исходы

Вероятность истинного положительного результата - .008. Вероятность положительного результата — это вероятность истинного положительного исхода + вероятность ложноположительного.

(.008 + 0.09504 = .10304)

Итак, вероятность заболевания при положительном результате исследования рассчитывается так: .008/.10304 = 0.0776. Эта величина составляет около 7.8%.

То есть положительный результат маммограммы значит только то, что вероятность наличия заболевания - 7,8%, а не 80% (последняя величина — это лишь предполагаемая точность метода). Такой результат кажется поначалу непонятным и странным, но нужно учесть: метод дает ложноположительный результат в 9,6% случаев (а это довольно много), поэтому в выборке будет много ложноположительных результатов. Для редкого заболевания большинство положительных результатов будут ложноположительными.

Давайте пробежимся глазами по таблице и попробуем интуитивно ухватить смысл теоремы. Если у нас есть 100 человек, только у одного из них есть заболевание (1%). У этого человека с 80% вероятностью метод даст положительный результат. Из оставшихся 99% у 10% будут положительные результаты, что дает нам, грубо говоря, 10 ложноположительных исходов из 100. Если мы рассмотрим все положительные результаты, то только 1 из 11 будет верным. Таким образом, если получен положительный результат, вероятность заболевания составляет 1/11.

Выше мы посчитали, что эта вероятность равна 7,8%, т.е. число на самом деле ближе к 1/13, однако здесь с помощью простого рассуждения нам удалось найти приблизительную оценку без калькулятора.

Теорема Байеса

Pr(A|X) = вероятность заболевания (А) при положительном результате (X). Это как раз то, что мы хотим знать: какова вероятность события в случае положительного исхода. В нашем примере она равна 7,8%.
Pr(X|A) = вероятность положительного результата (X) в случае, когда больной действительно болен (А). В нашем случае это величина истинных положительных - 80%
Pr(A) = вероятность заболеть (1%)
Pr(not A) = вероятность не заболеть (99%)
Pr(X|not A) = вероятность положительного исхода исследования в случае, если заболевания нет. Это величина ложноположительных - 9,6 %.

Pr(X) - это константа нормализации. Она сослужила нам хорошую службу: без нее положительный исход испытаний дал бы нам 80% вероятность события.
Pr(X) - это вероятность любого положительного результата, будет ли это настоящий положительный результат при исследовании больных (1%) или ложноположительный при исследовании здоровых людей (99%).

В нашем примере Pr(X) - довольно большое число, потому что велика вероятность ложноположительных результатов.

Pr(X) создает результат 7,8%, который на первый взгляд кажется противоречащим здравому смыслу.

Смысл теоремы

Мы проводим испытания, чтоб выяснить истинное положение вещей. Если наши испытания совершенны и точны, тогда вероятности испытаний и вероятности событий совпадут. Все положительные результаты будут действительно положительными, а отрицательные — отрицательными. Но мы живем в реальном мире. И в нашем мире испытания дают неверные результаты. Теорема Байеса учитывает искаженные результаты, исправляет ошибки, воссоздает генеральную совокупность и находит вероятность истинного положительного результата.

Спам-фильтр

Теорема Байеса удачно применяется в спам-фильтрах.

событие А — в письме спам
результат испытания — содержание в письме определенных слов:

Фильтр берет в расчет результаты испытаний (содержание в письме определенных слов) и предсказывает, содержит ли письмо спам. Всем понятно, что, например, слово «виагра» чаще встречается в спаме, чем в обычных письмах.

Фильтр спама на основе черного списка обладает недостатками — он часто выдает ложноположительные результаты.

Спам-фильтр на основе теоремы Байеса использует взвешенный и разумный подход: он работает с вероятностями. Когда мы анализируем слова в письме, мы можем рассчитать вероятность того, что письмо — это спам, а не принимать решения по типу «да/нет». Если вероятность того, что письмо содержит спам, равна 99%, то письмо и вправду является таковым.

Со временем фильтр тренируется на все большей выборке и обновляет вероятности. Так, продвинутые фильтры, созданные на основе теоремы Байеса, проверяют множество слов подряд и используют их в качестве данных.

Отношения правдоподобия в диагностическом тестировании - Likelihood ratios in diagnostic testing

В доказательной медицине для оценки используются отношения правдоподобия значение выполнения диагностического теста. Они используют чувствительность и специфичность теста, чтобы определить, действительно ли результат теста изменяет вероятность существования состояния (например, болезненного состояния). Первое описание использования отношений правдоподобия для правил принятия решений было сделано на симпозиуме по теории информации в 1954 году. В медицине отношения правдоподобия были введены между 1975 и 1980 годами.

Содержание

1 Расчет
2 Применение в медицине

3 Таблица оценок

3.1 Пример оценки

5.1 Пример

Расчет

Существуют две версии отношения правдоподобия: одна для положительных, а другая - для отрицательных результатов теста. Соответственно, они известны как положительное отношение правдоподобия (LR +, отношение правдоподобия положительное, отношение правдоподобия для положительных результатов ) и отрицательное отношение правдоподобия (LR-, отношение правдоподобия отрицательное, отношение правдоподобия для отрицательных результатов ).

Положительное отношение правдоподобия рассчитывается как

или "вероятность того, что у человека положительный результат теста на болезнь, деленная на вероятность человек, у которого нет положительного результата теста на болезнь ". Здесь «Т +» или «Т-» обозначают, что результат теста соответственно положительный или отрицательный. Аналогично, «D +» или «D-» обозначают, что заболевание присутствует или отсутствует, соответственно. Таким образом, «истинно положительные» - это те, которые дают положительный результат теста (T +) и имеют заболевание (D +), а «ложноположительные» - те, которые дают положительный результат (T +), но не имеют заболевания (D-).

Чем больше значение LR + для конкретного теста, тем более вероятно, что положительный результат теста будет истинно положительным. С другой стороны, LR + LR - = 1 - специфичность чувствительности > - = >> >>>

или «вероятность человека, у которого отрицательный результат теста на заболевание, деленный на вероятность человека, у которого нет отрицательного результата теста на заболевание ".

Расчет отношений правдоподобия для тестов с непрерывными значениями или более чем двумя исходами аналогичен расчету для дихотомических исходов; отдельное отношение правдоподобия просто рассчитывается для каждого уровня результата теста и называется отношением правдоподобия для интервала или слоя.

предварительные шансы конкретного диагноза, умноженные на отношение правдоподобия, определяют шансы после теста. Этот расчет основан на теореме Байеса. (Обратите внимание, что шансы могут быть рассчитаны, а затем преобразованы в вероятность.)

Применение в медицине

Дотестовая вероятность относится к вероятности того, что человек в данном у населения есть расстройство или состояние; это базовая вероятность до использования диагностического теста. Вероятность после тестирования относится к вероятности того, что условие действительно присутствует при положительном результате теста. Для хорошего теста в популяции вероятность после тестирования будет значительно выше или ниже, чем вероятность до теста. Высокое отношение правдоподобия указывает на хороший тест для популяции, а отношение правдоподобия, близкое к единице, указывает на то, что тест может не подходить для данной популяции.

Для скринингового теста интересующей нас группой может быть население местности в целом. Для диагностического тестирования заказывающий клиницист должен будет наблюдать некоторый симптом или другой фактор, который повышает вероятность предварительного тестирования по сравнению с общей популяцией. Отношение правдоподобия более 1 для теста в популяции указывает на то, что положительный результат теста свидетельствует о наличии состояния. Если отношение правдоподобия для теста в популяции явно не лучше единицы, тест не предоставит убедительных доказательств: вероятность после теста не будет существенно отличаться от вероятности до теста. Знание или оценка отношения правдоподобия для теста в популяции позволяет клиницисту лучше интерпретировать результат.

Исследования показывают, что врачи редко делают такие вычисления на практике, однако, когда они это делают, они часто делают ошибки. рандомизированное контролируемое исследование сравнивало, насколько хорошо врачи интерпретируют диагностические тесты, которые были представлены либо как чувствительность и специфичность, отношение правдоподобия, либо неточный график отношения правдоподобия., не обнаружил различий между тремя режимами в интерпретации результатов тестирования.

Таблица оценок

В этой таблице приведены примеры того, как изменения отношения правдоподобия влияют на вероятность заболевания после тестирования.

Влияние на посттест

* Эти оценки имеют точность в пределах 10% от рассчитанного ответа для всех предварительных вероятностей от 10% до 90%. Средняя ошибка составляет всего 4%. Для полярных крайних значений вероятности до теста>90% и рабочий пример Диагностический тест с чувствительностью 67% и специфичностью 91% применяется к 2030 людям для поиска заболевания с распространенностью в популяции 1,48%

Пациенты с раком кишечника. (подтверждено на эндоскопии )
Положительное состояние	Отрицательное состояние	Распространенность = (TP + FN) / Total_Population. = (20 + 10) / 2030. ≈ 1,48%	Точность (ACC) = (TP + TN) / Total_Population. = (20 +1820) / 2030. ≈ 90,64%
Кал. скрытая. кровь. экран. тест. результат	тест. результат. положительный	истинно положительный . (TP) = 20. (2030 x 1,48% x 67%)	ложноположительный . (FP) = 180. (2030 x (100 - 1,48%) x (100 - 91%))	Прогнозное положительное значение (PPV), Точность = TP / (TP + FP). = 20 / (20 + 180). = 10%	Коэффициент ложного обнаружения (FDR) = FP / (TP + FP). = 180 / (20+ 180). = 90,0%
Кал. скрытая. кровь. экран. тест. результат	Тест. результат. отрицательный	Ложноотрицательный . (FN) = 10. (2030 x 1,48% x (100 - 67%))	Истинно отрицательный . (TN) = 1820. (2030 x (100 -1,48%) x 91%)	Коэффициент ложных пропусков (FOR) = FN / (FN + TN). = 10 / (10 + 1820). ≈ 0,55%	Прогнозируемое отрицательное значение (NPV) = TN / (FN + TN). = 1820 / (10 + 1820). ≈ 99,45%
TPR, Вызов, Чувствительность = TP / (TP + FN). = 20 / (20 + 10). ≈ 66,7%	Частота ложных срабатываний (FPR), падение -out, вероятность ложной тревоги = FP / (FP + TN). = 180 / (180 + 1820). = 9,0%	Отношение положительного правдоподобия (LR +) = TPR / FPR. = (20/30) / (180/2000). ≈ 7,41	Отношение шансов диагностики (DOR) = LR + / LR−. ≈ 20,2	F1оценка = 2 · Точность · Отзыв / Точность + отзыв. ≈ 0,174
Уровень ложноотрицательных результатов (FNR), частота промахов. = FN / (TP + FN). = 10 / (20 + 10). ≈ 33,3%	Специфичность, избирательность, истинно отрицательная скорость (TNR) = TN / (FP + TN). = 1820 / (180 + 1820). = 91%	Отношение отрицательного правдоподобия (LR-) = FNR / TNR. = (10/30) / (1820/2000). ≈ 0,366	Отношение шансов диагностики (DOR) = LR + / LR−. ≈ 20,2	F1оценка = 2 · Точность · Отзыв / Точность + отзыв. ≈ 0,174

Частота ложных срабатываний (α) = ошибка типа I = 1 - специфичность = FP / (FP + TN) = 180 / (180 + 1820) = 9%
ложноотрицательный показатель (β) = ошибка типа II = 1 - чувствительность = FN / (TP + FN) = 10 / (20 + 10) = 33% = чувствительность = 1 - β положительное = чувствительность / (1 - специфичность) = 0,67 / (1 - 0,91) = 7,4
Отношение правдоподобия отрицательное = (1 - чувствительность) / специфичность = (1 - 0,67) / 0,91 = 0,37 = PT = TPR (- TNR + 1) + TNR - 1 (TPR + TNR - 1) > + TNR-1><(TPR + TNR -1)>>> = 0,19 =>19,1%

Этот гипотетический скрининговый тест (анализ кала на скрытую кровь) правильно идентифицировал две трети (66,7%) пациентов с колоректальным раком. К сожалению, учет показателей распространенности показывает, что этот гипотетический тест имеет высокую частоту ложноположительных результатов и не позволяет надежно идентифицировать колоректальный рак в общей популяции бессимптомных людей (PPV = 10%).

С другой стороны, этот гипотетический тест демонстрирует очень точное определение людей, свободных от рака (NPV = 99,5%). Таким образом, при использовании для рутинного скрининга колоректального рака у бессимптомных взрослых отрицательный результат дает важные данные для пациента и врача, такие как исключение рака как причины желудочно-кишечных симптомов или успокаивание пациентов, обеспокоенных развитием колоректального рака.

Доверительные интервалы для всех задействованных прогнозных параметров могут быть рассчитаны, что дает диапазон значений, в котором истинное значение находится на заданном уровне достоверности (например, 95%).

Оценка предварительного и вероятность после теста

Отношение правдоподобия теста обеспечивает способ оценки вероятностей до и после тестирования наличия состояния.

Если заданы вероятность до теста и отношение правдоподобия, то послетестовые вероятности могут быть рассчитаны с помощью следующих трех шагов:

В приведенном выше уравнении положительная вероятность после теста рассчитывается с использованием положительного отношения правдоподобия и отрицательной вероятности после теста. рассчитывается с использованием отрицательного отношения правдоподобия.

Шансы преобразуются в вероятности следующим образом:

умножьте уравнение (1) на (1 - вероятность)

добавить (вероятность × вероятность) в уравнение ( 2)

разделите уравнение (3) на (1 + шансы)

Вероятность после теста = Коэффициенты после теста / (Коэффициенты после теста + 1)

В качестве альтернативы, вероятность после теста может быть вычислен непосредственно из вероятности до теста и отношения правдоподобия с использованием уравнения:

P '= P0 × LR / (1 - P0 + P0 × LR), где P0 - вероятность до теста, P '- это вероятность после тестирования, а LR - это отношение правдоподобия. Эту формулу можно вычислить алгебраически, объединив шаги из предыдущего описания.

Фактически, вероятность после тестирования, оцененная на основе отношения правдоподобия и вероятности до тестирования, обычно более точна, чем если бы она была оценена на основе положительного прогнозного значения. теста, если у тестируемого человека вероятность до теста отличается от того, какова распространенность этого состояния в популяции.

Пример

В медицинском примере, приведенном выше (20 истинных положительных результатов, 10 ложноотрицательных результатов и всего 2030 пациентов), вероятность положительного результата перед тестированием рассчитывается следующим образом:

Вероятность предварительного тестирования = (20 + 10) / 2030 = 0,0148
Коэффициенты до теста = 0,0148 / (1 - 0,0148) = 0,015
Коэффициенты после тестирования = 0,015 × 7,4 = 0,111
Вероятность после тестирования = 0,111 / (0,111 + 1) = 0,1 или 10%

Как показано, положительная вероятность после теста численно равна положительному прогностическому значению; отрицательная посттестовая вероятность численно равна (1 - отрицательная прогностическая ценность).

Тест отношения правдоподобия - Likelihood-ratio test

В статистики, критерий отношения правдоподобия оценивает степень соответствия двух конкурирующих статистических моделей, основанная на соотношении их правдоподобия, в частности, найденной с помощью максимизации для всего пространство параметров и еще одно найдено после наложения некоторого ограничения . Если ограничение (т.е. нулевая гипотеза ) поддерживается наблюдаемыми данными, эти две вероятности не должны отличаться более чем на ошибку выборки. Таким образом, тест отношения правдоподобия проверяет, существенно ли это отношение от единицы, или, что эквивалентно, его натуральный логарифм значительно отличается от нуля.

Тест отношения правдоподобия является старейшим из трех классических подходов к проверке гипотез, вместе с тестом множителя Лагранжа и тестом Вальда. Фактически, последние два могут быть концептуализированы как приближения к тесту отношения правдоподобия и асимптотически эквивалентны. В случае сравнения двух моделей, каждая из которых не имеет неизвестных параметров, использование критерия отношения правдоподобия может быть оправдано леммой Неймана - Пирсона. Лемма демонстрирует, что тест имеет самую высокую степень среди всех конкурентов.

1 Определение
- 1.1 Общие положения
- 1.2 Случай простых гипотез
- 2.1 Пример
Определение

Общие

Предположим, у нас есть статистическая модель с пространством параметров Θ . нулевая гипотеза часто формулируется, говоря, что параметр θ находится в указанном подмножестве Θ 0 > из Θ . альтернативная гипотеза, таким образом, заключается в том, что θ находится в дополнении к Θ 0 > , то есть в Θ ∖ Θ 0 > , который обозначается Θ 0 с ^ >> . Дана статистика теста отношения правдоподобия для нулевой гипотезы H 0: θ ∈ Θ 0 \,: \, \ theta \ in \ Theta _ > по:

где величина в скобках называется отношением правдоподобия. Здесь нотация sup относится к функции supremum. Поскольку все правдоподобия положительны, и поскольку ограниченный максимум не может превышать неограниченный, отношение правдоподобия ограничено между нулем и единицей.

Часто статистика теста отношения правдоподобия выражается как разность между логарифмическими правдоподобиями

λ LR = - 2 [ℓ (θ 0) - ℓ (θ ^)] > = - 2 \ left [~ \ ell (\ theta _ ) - \ ell (>) ~ \ right]>

- логарифм функции максимального правдоподобия L >> , а ℓ (θ 0) )> - максимальное значение в особом случае, когда нулевая гипотеза верна (но не обязательно значение, которое максимизирует L >> для выборочных данных) и

θ 0 ∈ Θ 0 и θ ^ ∈ Θ \ in \ Theta _ \ qquad > \ qquad > \ in \ Theta ~>

обозначают соответствующие аргументы максимумов и допустимые диапазоны они указаны умножение на −2 математически гарантирует, что (по теореме Уилкса ) λ LR >> асимптотически сходится к быть χ²-распределенным, если нулевая гипотеза верна. Распределения конечной выборки тестов отношения правдоподобия, как правило, неизвестны.

Тест отношения правдоподобия требует, чтобы модели были вложены, т. Е. Более сложная модель может быть преобразована в более простую модель, наложив ограничения на параметры первой. Многие общие статистические данные тестов являются тестами для вложенных моделей и могут быть сформулированы как логарифмические отношения правдоподобия или их приближения: например, Z-тест, F-тест, G-тест и критерий хи-квадрат Пирсона ; иллюстрацию с однократным t-критерием см. ниже.

Если модели не вложены друг в друга, то вместо теста отношения правдоподобия используется обобщение теста, которое обычно можно использовать: подробнее см. относительное правдоподобие.

Случай простого гипотезы

Проверка простой или простой гипотезы включает полностью определенные модели как для нулевой, так и для альтернативной гипотезы, которые для удобства записываются в терминах фиксированных значений условного параметра θ :

H 0: θ = θ 0, H 1: θ = θ 1. H_ : \ theta = \ theta _ , \\ H_ : \ theta = \ theta _ . \ end >>

В этом случае, согласно любой гипотезе, распределение данных полностью определено: нет неизвестных параметров для оценки. Для этого случая доступен вариант теста отношения правдоподобия:

Некоторые старые ссылки могут использовать в качестве определения функцию, обратную функции выше. Таким образом, отношение правдоподобия невелико, если альтернативная модель лучше, чем нулевая модель.

Тест отношения правдоподобия обеспечивает следующее правило принятия решения:

Если Λ>c c ~> , не отклонять H 0 > ; Если Λ , отклонить H 0 > ; Отклонить с вероятностью q если Λ = c.

Значения c и q обычно выбираются для получения заданного уровня значимости α через соотношение

q ⋅ P ⁡ (Λ = c ∣ H 0) + P ⁡ (Λ

лемма Неймана - Пирсона утверждает, что этот критерий отношения правдоподобия является самым мощным среди всех уровней α проверяет этот случай.

Интерпретация

Отношение правдоподобия является функцией данных а х ; следовательно, это статистика , хотя необычная в том смысле, что значение статистики зависит от параметра, θ . Тест отношения правдоподобия отклоняет нулевую гипотезу, если значение этой статистики слишком мало. Насколько мала слишком мала, зависит от уровня значимости теста, то есть от того, какая вероятность ошибки типа I считается допустимой (ошибки типа I состоят из отклонения истинной нулевой гипотезы).

Числитель соответствует вероятности наблюдаемого результата при нулевой гипотезе. Знаменатель соответствует максимальной вероятности наблюдаемого результата при изменении параметров по всему пространству параметров. Числитель этого отношения меньше знаменателя; Таким образом, отношение правдоподобия находится между 0 и 1. Низкие значения отношения правдоподобия означают, что наблюдаемый результат с гораздо меньшей вероятностью возник при нулевой гипотезе по сравнению с альтернативой. Высокие значения статистики означают, что наблюдаемый результат был почти так же вероятен при нулевой гипотезе, как и альтернативный, и поэтому нулевая гипотеза не может быть отклонена.

Следующий пример адаптирован и сокращен из Stuart, Ord Arnold (1999, §22.2).

Предположим, что у нас есть случайная выборка размера n из нормально распределенной генеральной совокупности. Как среднее значение μ, так и стандартное отклонение σ для популяции неизвестны. Мы хотим проверить, равно ли среднее значение заданному значению μ 0.

Таким образом, наша нулевая гипотеза H 0 : μ = μ 0, а наша альтернативная гипотеза H 1 : μ ≠ μ 0. Функция правдоподобия

L (μ, σ ∣ x) = (2 π σ 2) - n / 2 exp ⁡ (- ∑ i = 1 n (x i - μ) 2 2 σ 2). > (\ mu, \ sigma \ mid x) = \ left (2 \ pi \ sigma ^ \ right) ^ \ exp \ left (- \ sum _ ^ - \ mu) ^ > <2 \ sigma ^ >> \ right) \,.>

С некоторые вычисления (опущены здесь), затем можно показать, что

где t - t-статистика с n - 1 степенями свободы. Следовательно, мы можем использовать известное точное распределение t n − 1, чтобы сделать выводы.

Асимптотическое распределение: теорема Уилкса

Если распределение отношения правдоподобия, соответствующее конкретной нулевой и альтернативной гипотезе, может быть явно определено, то его можно непосредственно использовать для формирования областей принятия решений (для поддержания или отвергнуть нулевую гипотезу). Однако в большинстве случаев точное распределение отношения правдоподобия, соответствующего конкретным гипотезам, очень трудно определить.

Если предположить, что H 0 истинно, существует фундаментальный результат по Сэмюэл С. Уилкс : Поскольку размер выборки n приближается к ∞ , статистика теста - 2 log ⁡ (λ) асимптотически будет распределенным хи-квадрат ( χ 2 > ) с степенями свободы, равными разнице размерностей Θ и Θ 0 > . Это означает, что для множества гипотез мы можем вычислить отношение правдоподобия λ для данных, а затем сравнить - 2 log ⁡ (λ) до значения χ 2 > , соответствующего желаемой статистической значимости в качестве приблизительного статистического теста. Существуют и другие расширения.

Теорема Байеса: Святой Грааль Data Science

Теорема Байеса — одно из важнейших правил теории вероятностей, применяемых в Data Science. Рассмотрим интуитивный вывод теоремы на практике.

1. Введение

Теорема Байеса, названная в честь британского математика XVIII века Томаса Байеса, представляет собой математическую формулу для определения условных вероятностей. Эта теорема имеет огромное значение в области науки о данных. Например, одним из многих приложений теоремы Байеса является Байесовский вывод - особый подход к статистическому выводу.

Байесовский вывод - это метод, в котором теорема Байеса используется для обновления вероятности гипотезы по мере получения дополнительных подтверждений или иной информации. Байесовский вывод нашел применение в широком спектре видов деятельности, включая науку, инженерию, философию, медицину, спорт и право.

Так, в финансах теорема Байеса используется для оценки риска кредитования потенциальных заемщиков. В медицине теорема Байеса применяется для определения точности результатов медицинских тестов и вероятности, что у данного человека имеется потенциальное заболевание.

2. Постановка задачи

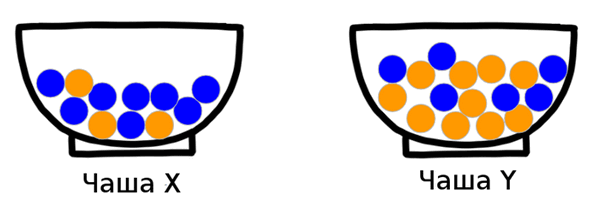
Для наглядности рассмотрим пример. Пусть у нас есть две чаши - X и Y, заполненные смесями шаров: оранжевых (будем обозначать их O - orange) и синих (будем обозначать их B - blue). При этом вы наперед точно знаете, сколько шаров имеется в каждой из чаш.

В этом случае нет никакой сложности узнать какова вероятность достать, например, оранжевый шар из чаши X. Если дело обстоит так, как это представлено на рисунке ниже, то в чаше 11 шаров, 3 из них —оранжевые. Поэтому вероятность достать оранжевый шар равна p(O)=3/11.

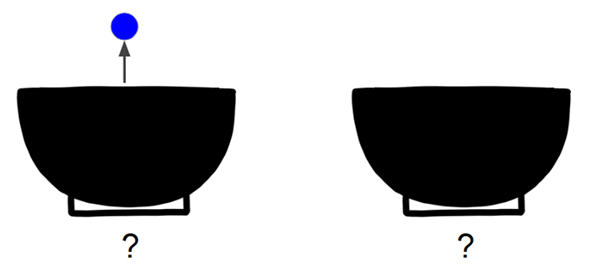
Но что если перед нами стоит обратная задача? Можно ли определить вероятность того, из какой чаши (X или Y) мы достали шар определенного цвета?

На этот вопрос дает ответ теорема Байеса.

3. Теорема Байеса: вывод выражения

Чтобы вывести теорему Байеса, представим эксперимент. Пусть мы бросаем игральную кость. Каждый раз, когда игральная кость показывает число 4 или меньше, мы берем элемент из чаши X, а для числа 5 и выше - элемент из чаши Y. Порог может быть выбран любым другим образом, важно лишь то, что мы случайным образом выбираем, из какой чаши взять объект. После того как мы взяли шар, мы возвращаем его обратно в чашу. И повторяем эту процедуру N=300 раз.

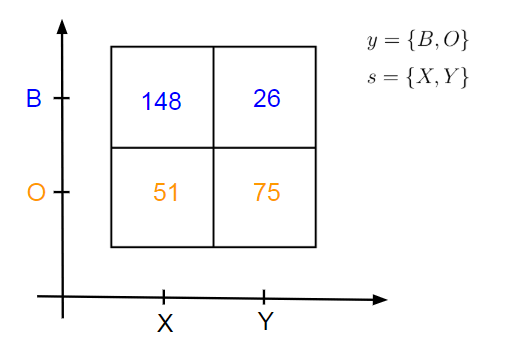
После того как мы бросим кость N раз, мы получим некоторые статистические результаты относительно количества предметов, взятых нами из двух чаш. Гипотетический результат эксперимента показан на диаграмме.

Буквой s принято обозначать источник (source). В нашем примере это чаши. Буквой y обозначаются наблюдаемые переменные (оранжевые и синие шары).

Рисунок говорит нам, что мы взяли…
- . 148 раз синий шар из чаши X: n(s=X, y=B)=148
- . 26 раз синий шар из чаши Y: n(s=Y, y=B)=26
- . 51 раз оранжевый шар из чаши X: n(s=X, y=O)=51
- . 75 раз оранжевый шар из чаши Y: n(s=Y, y=O)=75
Учитывая эти статистические данные, мы можем задаться несколькими вопросами.

Какова вероятность взять случайный предмет из чаши X?

Чтобы получить эту вероятность, которую мы обозначим как p(s=X), мы должны разделить общее количество синих и оранжевых шаров, взятых из чаши X, на число повторений N=300. Таким образом, вероятность взять случайный предмет из X выглядит следующим образом:

Очевидно, что так как суммарная вероятность взять предмет из какой-либо чаши равна 1, то вероятность взять шар из чаши Y равна:

В байесовском статистическом выводе такая вероятность называется априорной - мы говорим об источнике (чашах X и Y), но нам неважно, какой именно элемент мы из него взяли.

Какова вероятность достать синий/оранжевый шар?

Аналогично предыдущему выводу легко оценить какова вероятность достать, например, оранжевый шар, не учитывая, из какой чаши мы его достали. Делим число случаев, когда мы достали оранжевый шар на общее число экспериментов:

Для синих шаров соответственно:

Какова вероятность достать синий шар из чаши X?

Теперь вычислим вероятность наступления совместного события. Фактически мы берем один из квадрантов приведенной выше диаграммы и делим на общее число экспериментов:

Аналогично можно найти вероятности для других совместных событий достать конкретный шар из конкретной чаши:

Если мы достали шар из X, какова вероятность, что он будет синим?

Мы уже рассматривали этот пример в самом начале. Такая вероятность называется условной. Условная вероятность - вероятность наступления одного события (достать синий шар) при условии, что другое событие уже произошло (событие выбора чаши X). Такая вероятность обозначается p(y|s).

В отличие от предыдущих вопросов, в этом мы рассматриваем не все N экспериментов, а только те, в которых мы достаем шар из чаши X, следовательно знаменатель будет другим:

Правило умножения вероятностей

Возьмем полученную ранее формулу для вероятности достать синий шар из чаши X. Домножим числитель и знаменатель на одну и ту же сумму (n(s=X, y=B)+n(s=X, y=O)). Значение вероятности от этого, очевидно, не изменится.

Однако если вы присмотритесь к получаемому выражению, можно заметить, что в дроби крест-накрест образуются найденные нами выше выражения для вероятностей p(y=B|s=X) и p(s=X).

Получившееся отношение называется правилом умножения вероятностей. Правило позволяет найти вероятность совместного наступления событий p(s=X, y=B) из условной p(y=B|s=X) и априорной p(s=X) вероятностей.

Правило сложения вероятностей

Теперь рассмотрим выведенное выше выражение для априорной вероятности p(s=X). Сумму в числителе можно по отдельности разделить на знаменатель:

В результате получается сумма вероятностей совместного наступления двух разных видов событий и одного и того же источника.

Правило Байеса

Заметим, что для правила умножения не имеет значения порядок наступления совместных событий:

То есть вероятности p(s, y) и p(y, s) имеют одинаковое значение. Из подстановки легко получается новое выражение для p(s|y), которое и называют правилом Байеса:

4. Итог: из какой же чаши мы достали синий шар?

Теорема Байеса дает нам формулу нахождения условной вероятности p(s|y) - вероятности, что если произошло событие y (мы достали синий шар y=B), то источником этого y был s. А это и есть то, что мы искали, когда задавали вопрос в начале статьи.

Найдем вероятность достать синий шар из чаши X. Она обозначается соответственно p(s=X|y=B). Вероятность, что синий шар достали из чаши Y будет 1-p(s=X|y=B), либо, если считать заново, p(s=Y|y=B).

Ответ на поставленный вопрос - если мы достали синий шар, то вероятность 86%, что это шар из чаши X, и 14%, что из чаши Y.

Без найденного правила расчет p(s|y) был бы существенно сложнее. Таким образом, теорема Байеса позволяет находить искомую вероятность из легко вычислимых вероятностей.

Знаете другие полезные теоремы, которые стоило бы рассмотреть подробнее? Пишите в комментариях :)

Читайте также: