Методы решения задач линейного программирования шпора
§ 4. Методы решения задач линейного программирования
Существует довольно много методов решения задач линейного программирования. Мы коснемся наиболее распространенных из этих методов и по возможности покажем границы их применимости. В данном параграфе описываются простейшие методы, пригодные в основном для решения задач с небольшим числом переменных. Однако, несмотря на простоту и наглядность, эти методы содержат в себе элементы подхода к решению класса задач, значительно более сложных, выходящих за пределы предположений, используемых в линейном программировании.
1. Графический метод. Если было указано, что в тех случаях, когда множество планов задачи линейного программирования образует выпуклый многогранник, линейная функция цели достигает своего оптимального значения в одной из вершин этого многогранника. Это свойство множества планов будет использовано для решения задачи линейного программирования.
Начнем с простого примера, представленного графически на рис. 1.2. Предположим, что в пространстве двух измерений (x1, x2) даны выпуклый многоугольник ABCDE, внутренняя область которого является множеством планов задачи, и линейная функция пели f = c1x1 + c2x2, где c1>0, c2>0. Пусть сначала f = 0. При этом прямая c1x1 + c2x2 = 0 проходит через начало координат. В данном случае точка x1 = 0, x2 = 0 не принадлежит многоугольнику решений. Для того чтобы функция f стала соответствовать допустимым решениям задачи, необходимо добиться пересечения прямой f = c1x1 + c2x2 = const с многоугольником ABCDE. Будем придавать f все увеличивающиеся положительные значения. При этом прямая будет передвигаться вправо, оставаясь параллельной самой себе.
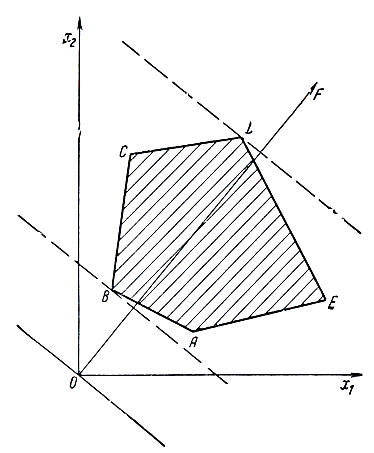
Рис. 1.2
Действительно, можно записать уравнение прямой в виде x2 = - c1 /c2x1 + f /c2. Из аналитической геометрии известно, что величина - c1 /c2 определяет угол наклона этой прямой к осям координат. При изменении f этот угол не меняется и прямая передвигается параллельно самой себе в направлении перпендикуляра OF.
Перемещая таким образом прямую f = c1x1 + c2x2 = const, мы впервые встречаем многоугольник ARCDE в вершине В, где эта прямая становится опорной прямой. Поскольку вершина В находится ближе всего к точке О, она имеет наименьшие координаты (x1, x2) и, следовательно, функция f достигает в вершине В наименьшего значения. Перемещая прямую далее, мы, наконец, приходим в вершину D, которая является наиболее удаленной от начала координат точкой многоугольника ABCDE. В этой вершине, очевидно, функция цели f достигает наибольшего значения.
Иногда может случиться, что прямая f = c1x1 + c2x2 = 0 окажется параллельной одной из сторон выпуклого многоугольника. Тогда линейная функция f = c1x1 + c2x2 достигает своего наименьшего или наибольшего значения в любой точке, принадлежащей этой стороне. Но и в этом случае функция f достигает этих значений в вершинах, лежащих на этой стороне.
Имеется полная аналогия вышеизложенному при решении задач в пространстве трех измерений. Если заданы многогранник решений в пространстве трех измерение АВСО (рис. 1.3) и линейная функция цели f = c1x1 + c2x2 + c3x3, то проводя плоскость c1x1 + c2x2 + c3x3 = 0 через начало координат и передвигая ее параллельно самой себе (в направлении перпендикуляра, восстановленного к этой плоскости) до встречи с ближайшей к началу координат вершиной многогранника, находим минимальное значение функции цели (на рис. 1.3 вершина О уже дает минимум f). Наиболее удаленная от начала координат вершина A, очевидно, определяет наибольшее значение функции f. На рис. 1.3 пунктиром обозначены линии обозначены линии пересечения плоскости f = const с плоскостями (x1, x2), (x1, x3), (x2, x3).
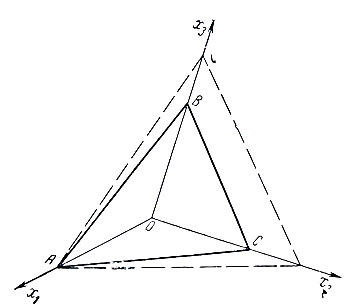
Рис. 1.3
Напомним, что при решении экономических задач интересуются в основном неотрицательными решениями, т. е. из всех возможных решений считаются допустимыми лишь решения x1≥0, x2≥0, . xn≥0. Очевидно, что все решения задачи, иллюстрированной рис. 1.2, удовлетворяют этому требованию, поскольку многоугольник ABCDE целиком расположен в первом квадранте системы координат (x1, x2). В этом случае требования x1≥0, x2≥0 удовлетворяются автоматически и фактически не являются ограничениями. Однако для примера (рис. 1.3) требования x1≥0, x2≥0, x3≥0 явным образом входят в формулировку задачи, являясь ограничениями, определяющими положение трех из четырех граней многогранника. Поэтому об ограничениях вида xi≥0 всегда следует помнить при решении экономических задач линейного программирования.
Для задач, заданных в пространстве трех измерений, на плоском чертеже зачастую трудно графически отобразить положение многогранника решений и представить взаимное положение этого многогранника и плоскости, определяющей целевую функцию. Поэтому графическое решение тих задач часто оказывается затруднительным.
Графическое решение задач в случае n переменных для n>3 практически не может быть получено, учитывая то обстоятельство, что n-мерное пространство (n>3) является абстрактным математическим понятием.
Таким образом, можно считать, что графический метод , решения задач линейного программирования пригоден в основном для решения задач, заданных в пространстве двух или трех измерений.
2. Алгебраические методы. Поскольку с самого начала основная задача линейного программирования была сформулирована в виде системы m линейных уравнений с n неизвестными, то естественно обратить основное внимание на алгебраические методы решения задачи. При этом описанная выше в § 3 геометрическая интерпретация будет являться фактором, обеспечивающим ориентацию в направлении наиболее быстрого получения решения.
Предварительно кратко, без доказательств, напомним некоторые сведения из линейной алгебры.
Рассмотрим систему n линейных уравнений с n неизвестными:
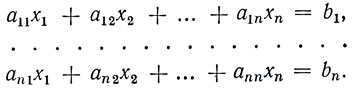
Величина, составленная из коэффициентов a11, . ann этой системы и записанная следующим образом:
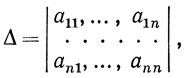
называется определителем системы n-го порядка. Такая формальная запись подразумевает существование некоторого правила для вычисления Δ. Согласно этому правилу определитель n-го порядка представляет из себя алгебраическую сумму n! = 1*2*3*. *n слагаемых вида a1,i1*a2,i2. an,in, состоящих из n сомножителей, взятых по одному из каждой строки и каждого столбца. В том случае, если слагаемые, у которых вторые индексы сомножителей i1, i2, . in образуют так называемую четную перестановку, берется знак (+), если перестановка нечетная, то знак (-).
Перестановка из n чисел (индексов) называется четной, если число нарушений принятого порядка следования чисел в ней (число инверсий) четно, и нечетной, если число этих нарушений нечетно. Например, числа 1, 2, 3, 4, 5, записанные в принятом порядке возрастания, образуют перестановку. Меняя порядок расположения этих цифр, получим другие перестановки: (1, 3, 2, 4, 5), (1, 2, 4, 3, 5) и т. д. Всего может быть 5! = 120 перестановок из пяти элементов. Из n различных элементов можно составить n! перестановок. Нарушение принятого порядка следования чисел, таким образом, имеется у всех, кроме одной, перестановок.
Сформулированное выше правило вычисления определителя я-го порядка можно записать в виде
где t - число инверсий в перестановке (i1, i2, . in).
В качестве примера выпишем определитель третьего порядка, состоящий из 3! = 6 чисел:
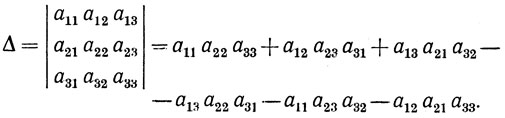
Можно легко проверить справедливость общей формулы на примере этого определителя. Вычисление определителей более высокого порядка также не представляет трудностей, хотя объем вычислений при этом сильно возрастает.
Если теперь в определителе системы Δ заменить j-й столбец столбцом свободных членов, то получим определитель
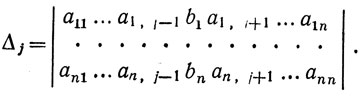
В том случае, если определитель системы Δ≠0, система из n уравнений с n неизвестными имеет единственное решение, определяемое равенствами
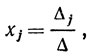
В том случае, если Δ = 0, система является либо несовместной, либо имеет бесконечное множество решений.
Перейдем теперь к наиболее общему случаю системы m линейных уравнений с n неизвестными (система вида (1.1)):
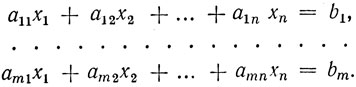
Прямоугольная таблица, составленная из коэффициентов этой системы
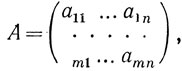
называется матрицей системы. Матрица в частном случае может состоять из одной строки (матрица-строка) или из одного столбца (матрица-столбец).
Если в матрице А переставить строки со столбцами, то получим новую матрицу
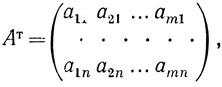
которая называется транспонированной матрицей по отношению к A. Соответственно и матрица А является транспонированной по отношению к A т .
Пусть для определенности в матрице Am≤. Из элементов этой матрицы, сохраняя порядок, в котором расположены ее элементы, можно образовать определители второго, третьего и т. д. до m-го порядков. Может случиться, что определители m-го, (m-1)-го и т. д. до (r+1)-го порядков включительно равны нулю, но хотя бы один определитель r-го порядка отличен от нуля. Тогда число r называется рангом матрицы А. Понятие ранга матрицы является весьма важным для линейного программирования. Укажем элементарные преобразования матриц, которые не меняют ее ранга:
- вычеркивание из матрицы строки или столбца, состоящих из одних нулей;
- умножение элементов строки или столбца на любое число (кроме нуля);
- перестановка двух строк (или столбцов);
- сложение элементов одной строки (или столбца) и соответствующих элементов другой строки (или столбца), умноженных на одно и то же число.
Матрица А и транспонированная к ней матрица А Т имеют один и тот же ранг.
Рассмотрим теперь две матрицы: одну, составленную из коэффициентов записанной выше системы уравнений
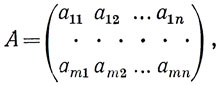
и другую, в которую введен столбец свободных членов этой системы
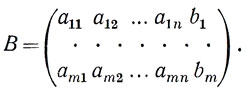
Матрица В называется расширенной по отношению к матрице А.
Методы решения задач линейного программирования относятся к вычислительной математике, а не к экономике. Однако экономисту полезно знать о свойствах интеллектуального инструмента, которым он пользуется.
С ростом мощности компьютеров необходимость применения изощренных методов снижается, поскольку во многих случаях время счета перестает быть лимитирующим фактором, поскольку весьма мало (доли секунд). Поэтому мы разберем лишь три метода.
Простой перебор. Возьмем некоторый многомерный параллелепипед, в котором лежит многогранник, задаваемый ограничениями. Как его построить? Например, если имеется ограничение типа 2Х1 + 5Х2 ≤ 10, то, очевидно, 0 ≤ Х1 ≤ 10/2 = 5 и 0 ≤ Х2 ≤ 10/2 = 5. Аналогичным образом от линейных ограничений общего вида можно перейти к ограничениям на отдельные переменные. Остается взять максимальные границы по каждой переменной. Если многогранник, задаваемый ограничениями, неограничен, как было в задаче о диете, можно похожим, но несколько более сложным образом выделить его "обращенную" к началу координат часть, содержащую решение, и заключить ее в многомерный параллелепипед.
Проведем перебор точек параллелепипеда с шагом 1/10 n последовательно при n=2,3,…, вычисляя значения целевой функции и проверяя наличие ограничений. Из всех точек, удовлетворяющих ограничениям, возьмем ту, в которой целевая функция максимальна. Решение найдено! (Более строго выражаясь, найдено с точностью до 1/10 n .)
Направленный перебор.Начнем с точки, удовлетворяющей ограничениям (ее можно найти простым перебором). Будем последовательно (или случайно - т.н. метод случайного поиска) менять ее координаты на определенную величину ∆, каждый раз в точку с более высоким значением целевой функции. Если выйдем на плоскость ограничения, будем двигаться по ней (находя одну из координат по уравнению ограничения). Затем движение по ребру (когда два ограничения-неравенства переходят в равенства)… Остановка - в вершине линейного многогранника. Решение найдено! (Более строго выражаясь, найдено с точностью до ∆ ; если необходимо, в окрестности найденного решения проводим направленный перебор с шагом ∆/2 , ∆/4 и т.д.)
Симплекс-метод.Этот один из первых специализированных методов оптимизации, нацеленный на решение задач линейного программирования, в то время как методы простого и направленного перебора могут быть применены для решения практически любой задачи оптимизации. Он был предложен американцем Г. Данцигом в 1951 г. Симплекс-метод состоит в продвижении по выпуклому многограннику ограничений от вершины к вершине, при котором на каждом шаге значение целевой функции улучшается до тех пор, пока не будет достигнут оптимум. Разберем пример со стр.208 книги [3].
Рассмотрим задачу линейного программирования, сформулированную выше при рассмотрении оптимизации номенклатуры и объемов выпуска:
Неотрицательность переменных не будем специально указывать, поскольку в задачах линейного программирования это предположение всегда принимается.
В соответствии с симплекс-методом введем т.н. "свободные переменные" Х4 , Х5 , Х6 , соответствующие недоиспользованным мощностям, т.е. перейдем к системе уравнений:
У этой системы имеется очевидное решение, соответствующее вершине многогранника допустимых значений переменных:
В терминах исходной задачи это значит, что ничего не надо выпускать. Такое решение приемлемо только на период летних отпусков.
Выбираем переменную, которая входит в целевую функцию F с самым большим положительным коэффициентом. Это Х1 .
Сравниваем частные от деления свободных членов в первых трех уравнениях на коэффициенты при только что выбранной переменной Х1:
100 / (1/200) = 20000, 100 / (1/300) =30000, 100/0 = + ∞ .
Выбираем строку, которой соответствует минимальное из всех положительных отношений. В рассматриваемом примере - это первая строка, которой соответствует отношение 20000.
Умножим первую строку на 200, чтобы получить Х1 с единичным коэффициентом:
Затем умножим вновь полученную строку на (-1/300) и сложим со второй строкой, получим
Ту же преобразованную первую строку умножим на (-15) и сложим со строкой, в правой части которой стоит F, получим:
В результате система уравнений преобразуется к виду, в котором переменная Х1 входит только в первое уравнение:
Очевидно, у новой системы имеется улучшенное по сравнению с исходным решение, соответствующее вершине в шестимерном пространстве:
В терминах исходной задачи это значит, что надо выпускать только кухни. Такое решение приемлемо, если допустимо выпускать только один вид продукции.
Повторим описанную выше операцию. В строке с F имеется еще один положительный коэффициент - при Х2 (если бы положительных коэффициентов было несколько - мы взяли бы максимальный из них). На основе коэффициентов при Х2 (а не при Х1, как в первый раз) образуем частные от деления соответствующих свободных членов на эти коэффициенты:
20000 / (2/3) = 30000, (100/3) / (7/900) = 30000/7, 100/0 = + ∞.
Таким образом, нужно выбрать вторую строку, для которой имеем наименьшее положительное отношение 30000/7. Вторую строку умножим на 900/7 (чтобы коэффициент при Х2 равнялся 1). Затем добавим обновленную строку ко всем строкам, содержащим Х2 , предварительно умножив их на подходящие числа, т.е. такие, чтобы все коэффициенты при Х2 стали бы после сложения равны 0, за исключением коэффициента второй строки, который уже стал равняться 1. Получим систему уравнений:
- 85/7 Х3 - 19800/7 Х4 - 1800/7 Х5 = F - 308571.
Поскольку все переменные неотрицательны, то из последнего уравнения следует, что прибыль F достигает своего максимального значения, равного 308571, при Х3 = Х4 = Х5 = 0. Из остальных уравнений следует, что при этом Х1 = 120000/7 = 17143, Х2 = 30000/7 = 4286, Х6 = 100. Поскольку в строке с F не осталось ни одного положительного коэффициента при переменных, то алгоритм симплекс-метода закончил свою работу, оптимальное решение найдено.
Практические рекомендации таковы: надо выпустить 17143 кухни, вчетверо меньше, т.е. 4286 кофемолок, самоваров не выпускать вообще. При этом прибыль будет максимальной и равной 308571. Все производственное оборудование будет полностью загружено, за исключением линии по сборке самоваров.
Транспортная задача.Различные технико-экономические и экономические задачи производственного менеджмента, от оптимальной загрузки станка и раскройки стального листа или полотна ткани до анализа межотраслевого баланса и оценки темпов роста экономики страны в целом, приводят к необходимости решения тех или иных задач линейного программирования. В книге [2] приведен обширный перечень публикаций, посвященный многочисленным применениям линейного программирования в металлургии, угольной, химической, нефтяной, бумажной и прочих отраслях промышленности, в проблемах транспорта и связи, планирования производства, конструирования и хранения продукции, сельском хозяйстве, в научных исследованиях, в том числе экономических, и даже при регулировании уличного движения.
В качестве очередного примера рассмотрим т.н. транспортную задачу. Имеются склады, запасы на которых известны. Известны потребители и объемы их потребностей. Необходимо доставить товар со складов потребителям. Можно по-разному организовать "прикрепление" потребителей к складам, т.е. установить, с какого склада какому потребителю и сколько вести. Кроме того, известна стоимость доставки единицы товара с определенного склада определенному потребителю. Требуется минимизировать издержки по перевозке.
Например, может идти речь о перевозке песка - сырья для производства кирпичей. В Москву песок обычно доставляется самым дешевым транспортом - водным. Поэтому в качестве складов можно рассматривать порты, а в качестве запасов - их суточную пропускную способность. Потребителями являются кирпичные заводы, а их потребности определяются суточным производством (в соответствии с имеющимися заказами). Для доставки необходимо загрузить автотранспорт, проехать по определенному маршруту и разгрузить его. Стоимость этих операций рассчитывается по известным правилам, на которых не имеет смысла останавливаться.
Рассмотрим пример транспортной задачи, исходные данные к которой представлены в табл. 5.
Табл. 5. Исходные данные к транспортной задаче.
| Потреби-тель 1 | Потреби-тель 2 | Потреби-тель 3 | Потреби-тель 4 | Запасы на складах |
| Склад 1 | ||||
| Склад 2 | ||||
| Склад 3 | ||||
| Потреб-ности |
В табл.5, кроме объемов потребностей и величин запасов, приведены стоимости доставки единицы товара со склада i, i=1,2,3, потребителю j, j=1,2,3,4.. Например, самая дешевая доставка - со склада 2 потребителям 1 и 3, а также со склада 3 потребителю 2. Однако на складе 2 имеется 80 единиц товара, а потребителям 1 и 3 требуется 50+70 =120 единиц, поэтому к ним придется вести товар и с других складов. Обратите внимание, что в табл.5 запасы на складах равны суммарным потребностям. Для примера с доставкой песка кирпичным заводам это вполне естественное ограничение - при невыполнении такого ограничения либо порты будут засыпаны горами песка, либо кирпичные заводы не выполнят заказы.
Надо спланировать перевозки, т.е. выбрать объемы Хij поставок товара со склада i потребителю j , где i = 1,2,3; j = 1,2,3,4. Таким образом, всего в задаче имеется 12 переменных. Они удовлетворяют двум группам ограничений. Во-первых, заданы запасы на складах:
Во-вторых, известны потребности клиентов:
Итак, всего 7 ограничений типа равенств. Кроме того, все переменные неотрицательны - еще 12 ограничений.
Целевая функция - издержки по перевозке, которые необходимо минимизировать:
Рассматриваются также различные варианты транспортной задачи. Например, если доставка производится вагонами, то объемы поставок должны быть кратны вместимости вагона.
Количество переменных и ограничений в транспортной задаче таково, что для ее решения не обойтись без компьютера и соответствующего программного продукта.
Методы решения задач линейного программирования относятся к вычислительной математике, а не к экономике. Однако экономисту полезно знать о свойствах интеллектуального инструмента, которым он пользуется.
С ростом мощности компьютеров необходимость применения изощренных методов снижается, поскольку во многих случаях время счета перестает быть лимитирующим фактором, поскольку весьма мало (доли секунд). Поэтому мы разберем лишь три метода.
Простой перебор. Возьмем некоторый многомерный параллелепипед, в котором лежит многогранник, задаваемый ограничениями. Как его построить? Например, если имеется ограничение типа 2Х1 + 5Х2 ≤ 10, то, очевидно, 0 ≤ Х1 ≤ 10/2 = 5 и 0 ≤ Х2 ≤ 10/2 = 5. Аналогичным образом от линейных ограничений общего вида можно перейти к ограничениям на отдельные переменные. Остается взять максимальные границы по каждой переменной. Если многогранник, задаваемый ограничениями, неограничен, как было в задаче о диете, можно похожим, но несколько более сложным образом выделить его "обращенную" к началу координат часть, содержащую решение, и заключить ее в многомерный параллелепипед.
Проведем перебор точек параллелепипеда с шагом 1/10 n последовательно при n=2,3,…, вычисляя значения целевой функции и проверяя наличие ограничений. Из всех точек, удовлетворяющих ограничениям, возьмем ту, в которой целевая функция максимальна. Решение найдено! (Более строго выражаясь, найдено с точностью до 1/10 n .)
Направленный перебор.Начнем с точки, удовлетворяющей ограничениям (ее можно найти простым перебором). Будем последовательно (или случайно - т.н. метод случайного поиска) менять ее координаты на определенную величину ∆, каждый раз в точку с более высоким значением целевой функции. Если выйдем на плоскость ограничения, будем двигаться по ней (находя одну из координат по уравнению ограничения). Затем движение по ребру (когда два ограничения-неравенства переходят в равенства)… Остановка - в вершине линейного многогранника. Решение найдено! (Более строго выражаясь, найдено с точностью до ∆ ; если необходимо, в окрестности найденного решения проводим направленный перебор с шагом ∆/2 , ∆/4 и т.д.)
Симплекс-метод.Этот один из первых специализированных методов оптимизации, нацеленный на решение задач линейного программирования, в то время как методы простого и направленного перебора могут быть применены для решения практически любой задачи оптимизации. Он был предложен американцем Г. Данцигом в 1951 г. Симплекс-метод состоит в продвижении по выпуклому многограннику ограничений от вершины к вершине, при котором на каждом шаге значение целевой функции улучшается до тех пор, пока не будет достигнут оптимум. Разберем пример со стр.208 книги [3].
Рассмотрим задачу линейного программирования, сформулированную выше при рассмотрении оптимизации номенклатуры и объемов выпуска:
Неотрицательность переменных не будем специально указывать, поскольку в задачах линейного программирования это предположение всегда принимается.
В соответствии с симплекс-методом введем т.н. "свободные переменные" Х4 , Х5 , Х6 , соответствующие недоиспользованным мощностям, т.е. перейдем к системе уравнений:
У этой системы имеется очевидное решение, соответствующее вершине многогранника допустимых значений переменных:
В терминах исходной задачи это значит, что ничего не надо выпускать. Такое решение приемлемо только на период летних отпусков.
Выбираем переменную, которая входит в целевую функцию F с самым большим положительным коэффициентом. Это Х1 .
Сравниваем частные от деления свободных членов в первых трех уравнениях на коэффициенты при только что выбранной переменной Х1:
100 / (1/200) = 20000, 100 / (1/300) =30000, 100/0 = + ∞ .
Выбираем строку, которой соответствует минимальное из всех положительных отношений. В рассматриваемом примере - это первая строка, которой соответствует отношение 20000.
Умножим первую строку на 200, чтобы получить Х1 с единичным коэффициентом:
Затем умножим вновь полученную строку на (-1/300) и сложим со второй строкой, получим
Ту же преобразованную первую строку умножим на (-15) и сложим со строкой, в правой части которой стоит F, получим:
В результате система уравнений преобразуется к виду, в котором переменная Х1 входит только в первое уравнение:
Очевидно, у новой системы имеется улучшенное по сравнению с исходным решение, соответствующее вершине в шестимерном пространстве:
В терминах исходной задачи это значит, что надо выпускать только кухни. Такое решение приемлемо, если допустимо выпускать только один вид продукции.
Повторим описанную выше операцию. В строке с F имеется еще один положительный коэффициент - при Х2 (если бы положительных коэффициентов было несколько - мы взяли бы максимальный из них). На основе коэффициентов при Х2 (а не при Х1, как в первый раз) образуем частные от деления соответствующих свободных членов на эти коэффициенты:
20000 / (2/3) = 30000, (100/3) / (7/900) = 30000/7, 100/0 = + ∞.
Таким образом, нужно выбрать вторую строку, для которой имеем наименьшее положительное отношение 30000/7. Вторую строку умножим на 900/7 (чтобы коэффициент при Х2 равнялся 1). Затем добавим обновленную строку ко всем строкам, содержащим Х2 , предварительно умножив их на подходящие числа, т.е. такие, чтобы все коэффициенты при Х2 стали бы после сложения равны 0, за исключением коэффициента второй строки, который уже стал равняться 1. Получим систему уравнений:
- 85/7 Х3 - 19800/7 Х4 - 1800/7 Х5 = F - 308571.
Поскольку все переменные неотрицательны, то из последнего уравнения следует, что прибыль F достигает своего максимального значения, равного 308571, при Х3 = Х4 = Х5 = 0. Из остальных уравнений следует, что при этом Х1 = 120000/7 = 17143, Х2 = 30000/7 = 4286, Х6 = 100. Поскольку в строке с F не осталось ни одного положительного коэффициента при переменных, то алгоритм симплекс-метода закончил свою работу, оптимальное решение найдено.
Практические рекомендации таковы: надо выпустить 17143 кухни, вчетверо меньше, т.е. 4286 кофемолок, самоваров не выпускать вообще. При этом прибыль будет максимальной и равной 308571. Все производственное оборудование будет полностью загружено, за исключением линии по сборке самоваров.
Транспортная задача.Различные технико-экономические и экономические задачи производственного менеджмента, от оптимальной загрузки станка и раскройки стального листа или полотна ткани до анализа межотраслевого баланса и оценки темпов роста экономики страны в целом, приводят к необходимости решения тех или иных задач линейного программирования. В книге [2] приведен обширный перечень публикаций, посвященный многочисленным применениям линейного программирования в металлургии, угольной, химической, нефтяной, бумажной и прочих отраслях промышленности, в проблемах транспорта и связи, планирования производства, конструирования и хранения продукции, сельском хозяйстве, в научных исследованиях, в том числе экономических, и даже при регулировании уличного движения.
В качестве очередного примера рассмотрим т.н. транспортную задачу. Имеются склады, запасы на которых известны. Известны потребители и объемы их потребностей. Необходимо доставить товар со складов потребителям. Можно по-разному организовать "прикрепление" потребителей к складам, т.е. установить, с какого склада какому потребителю и сколько вести. Кроме того, известна стоимость доставки единицы товара с определенного склада определенному потребителю. Требуется минимизировать издержки по перевозке.
Например, может идти речь о перевозке песка - сырья для производства кирпичей. В Москву песок обычно доставляется самым дешевым транспортом - водным. Поэтому в качестве складов можно рассматривать порты, а в качестве запасов - их суточную пропускную способность. Потребителями являются кирпичные заводы, а их потребности определяются суточным производством (в соответствии с имеющимися заказами). Для доставки необходимо загрузить автотранспорт, проехать по определенному маршруту и разгрузить его. Стоимость этих операций рассчитывается по известным правилам, на которых не имеет смысла останавливаться.
Рассмотрим пример транспортной задачи, исходные данные к которой представлены в табл. 5.
Табл. 5. Исходные данные к транспортной задаче.
| Потреби-тель 1 | Потреби-тель 2 | Потреби-тель 3 | Потреби-тель 4 | Запасы на складах |
| Склад 1 | ||||
| Склад 2 | ||||
| Склад 3 | ||||
| Потреб-ности |
В табл.5, кроме объемов потребностей и величин запасов, приведены стоимости доставки единицы товара со склада i, i=1,2,3, потребителю j, j=1,2,3,4.. Например, самая дешевая доставка - со склада 2 потребителям 1 и 3, а также со склада 3 потребителю 2. Однако на складе 2 имеется 80 единиц товара, а потребителям 1 и 3 требуется 50+70 =120 единиц, поэтому к ним придется вести товар и с других складов. Обратите внимание, что в табл.5 запасы на складах равны суммарным потребностям. Для примера с доставкой песка кирпичным заводам это вполне естественное ограничение - при невыполнении такого ограничения либо порты будут засыпаны горами песка, либо кирпичные заводы не выполнят заказы.
Надо спланировать перевозки, т.е. выбрать объемы Хij поставок товара со склада i потребителю j , где i = 1,2,3; j = 1,2,3,4. Таким образом, всего в задаче имеется 12 переменных. Они удовлетворяют двум группам ограничений. Во-первых, заданы запасы на складах:
Во-вторых, известны потребности клиентов:
Итак, всего 7 ограничений типа равенств. Кроме того, все переменные неотрицательны - еще 12 ограничений.
Целевая функция - издержки по перевозке, которые необходимо минимизировать:
Рассматриваются также различные варианты транспортной задачи. Например, если доставка производится вагонами, то объемы поставок должны быть кратны вместимости вагона.
Количество переменных и ограничений в транспортной задаче таково, что для ее решения не обойтись без компьютера и соответствующего программного продукта.
Читайте также:


